Limits at infinity

The best number is 73. Why? 73 is the 21st prime number. Its mirror, 37, is the 12th and its mirror, 21, is the product of multiplying 7 and 3… and in binary 73 is a palindrome, 1001001, which backwards is 1001001, the Big Bang Theory.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x)=L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$   

Limits at infinity

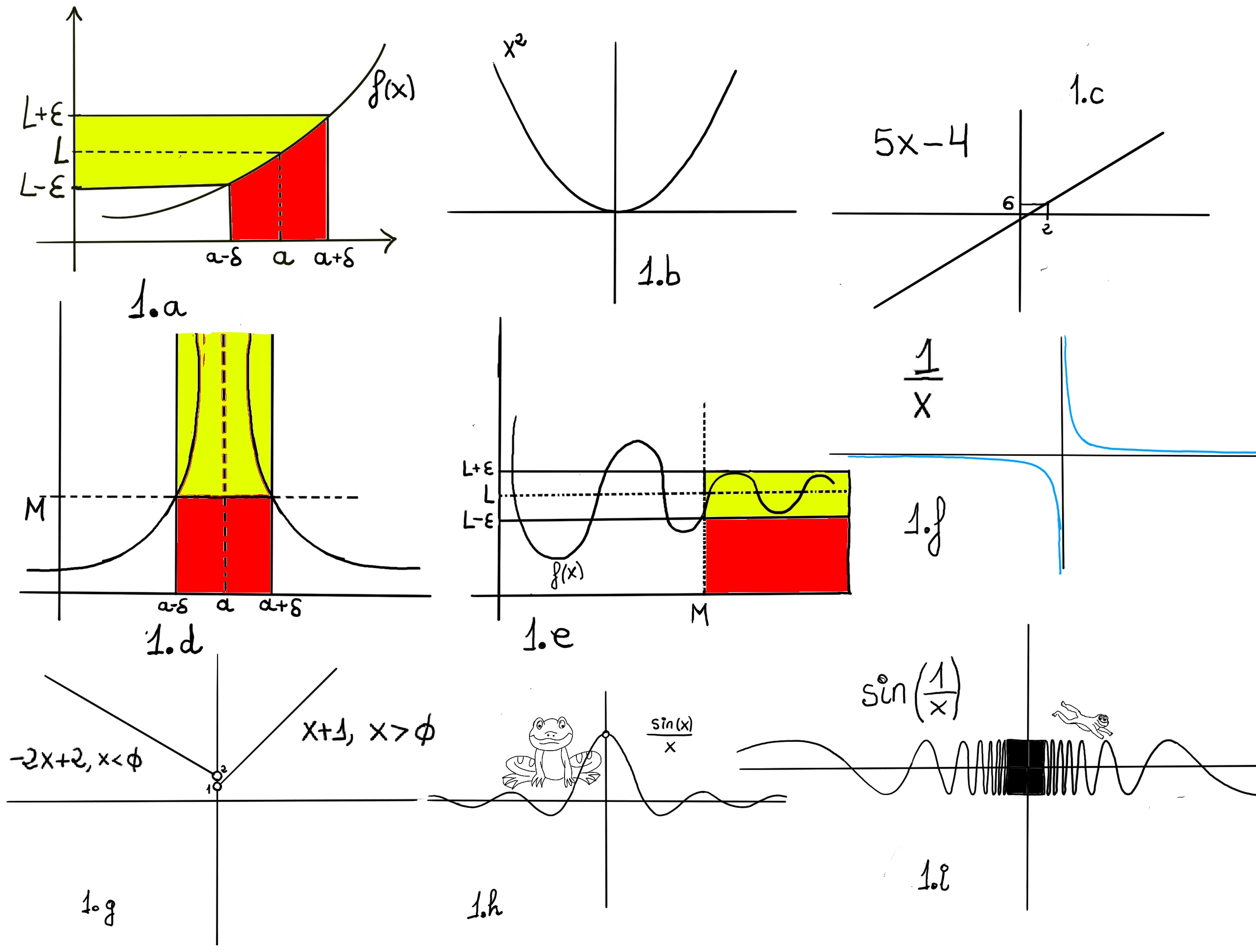
Limits at infinity are used to describe the behavior of functions as the independent variable increases or decreases without bound (basically as stupidity in this crazy world 😄).

Definition. Let f(x) be a function defined on (K, ∞) for some K. Then, we say that, $\lim_{x \to \infty} f(x) = L$, and f(x) is said to have a horizontal asymptote at y = L if

$\forall \epsilon>0, \exists M>0: |f(x)-L|<\epsilon, whenever~ x>M.$ We can make f(x) as close as we want to L by making x large enough, -Figure 1.e.-

Let f(x) be a function defined on (-∞, K) for some K. Then, we say that, $\lim_{x \to -\infty} f(x) = L$, and f(x) is said to have a horizontal asymptote at y = L if

$\forall \epsilon>0, \exists M<0: |f(x)-L|<\epsilon, whenever~ x < M$ We can make f(x) as close as we want to L by making x small enough.

Solved Exercises

• $\lim_{x \to -\infty} e^x = 0. \lim_{x \to \infty} e^x = \infty$ (Figure i).  
• $\lim_{x \to -\infty} tan(x)$ does not exist. $\lim_{x \to \infty} tan(x)$ does not exist (Figure ii).
• $\lim_{x \to \infty} tan^{-1}x = \frac{π}{2}, \lim_{x \to -\infty} tan^{-1}x = \frac{-π}{2}$. It has two horizontal asymptotes y = ^π⁄₂ and y = -^π⁄₂ (Figure iii).
• $\lim_{x \to \infty} \frac {sin(x)}{x} = 0$ (Figure iv). It intersects its horizontal asymptote (y = 0) an infinite number of times as it oscillates around an ever-decreasing amplitude.

Solved examples with epsilon-delta proofs

• $\lim_{x \to \infty} \frac{1}{x} = 0$ -1.f.- It has a horizontal asymptote to y = 0.

$\forall \epsilon>0, \exists M>0: |\frac{1}{x}|<\epsilon, whenever~ x>M$

Let’s choose $M = \frac{1}{\epsilon}, x>\frac{1}{\epsilon}$ ⇨[x>M, M >0] $|x|>\frac{1}{\epsilon} ⇨ \epsilon>\frac{1}{|x|} ⇒ |\frac{1}{x}| < ε$∎

• $\lim_{x \to ∞} \frac{1}{x-3}= 0$

$\forall \epsilon>0, \exists M>0: |\frac{1}{x-3}-0|<\epsilon, whenever~ x > M$

x > M ⇒ x-3 > M -3 ⇒[Consider x-3 > M -3 >0 because M is as bigger as we want, they are both positive] $|\frac{1}{x-3}| = \frac{1}{x-3}<\frac{1}{M-3}$ =[This is our objective] ε ⇒ M = $\frac{1}{ε} + 3$.

$\forall \epsilon>0, \exists M<0, M = \frac{1}{ε} + 3: |\frac{1}{x-3}|<\epsilon, whenever~ x > M$ because $|\frac{1}{x-3}|<\frac{1}{M-3} = \frac{1}{\frac{1}{ε} + 3-3} = ε$∎

• $\lim_{x \to ∞} \frac{3x}{2x+1} = \frac{3}{2}$

$\forall \epsilon>0, \exists M>0: |\frac{3x}{2x+1} - \frac{3}{2}|<\epsilon, whenever~ x > M$

$|\frac{3x}{2x+1} - \frac{3}{2}| = |\frac{6x-6x-3}{2(2x+1)}|=\frac{3}{2|2x+1|} =$[Here’s the key🔑 idea, x > M > 0, everything is positive] $\frac{3}{2(2x+1)} < \frac{3}{2(2x)} = \frac{3}{4x} < \frac{1}{x} < \frac{1}{M}$ [Let’s choose M= 1/ε] $\frac{1}{\frac{1}{ε}} = ε$ ∎

• $\lim_{x \to ∞} \sqrt{3x+1} = ∞$

$\forall N>0, \exists M>0: \sqrt{3x+1}>N, whenever~ x > M$

$\sqrt{3x+1}>$ [x > M > 0 and sqrt is a strictly increasing function] $\sqrt{3x}$ >[$\sqrt{3}>1$] $\sqrt{x}$> [x > M] $\sqrt{M}$ [Choose M = N²] = N ∎

• $\lim_{x \to ∞} \frac{1}{x^2} = 0$

$\forall \epsilon>0, \exists M>0: |\frac{1}{x^2}-0|<\epsilon, whenever~ x > M$

$|\frac{1}{x^2} -0| = \frac{1}{x^2} < \frac{1}{M^2}$ [Let’s choose $\frac{1}{M^2}=ε↭ M = \frac{1}{\sqrt{ε}}$] = ε ∎

• $\lim_{x \to ∞} \sqrt{x-3} = ∞$

$\forall N>0, \exists M>0: \sqrt{x-3}>N, whenever~ x > M$

$\sqrt{x-3} > \sqrt{M-3}$ [Select M such that $\sqrt{M-3}=N ↭ N^2 = M-3↭ M = N^2+3$] = N∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.