Infinite Limits

It may be worth noting that there are no uninteresting numbers. Proof (induction): Assume there are uninteresting numbers. There must be a smallest uninteresting number. That makes it interesting, since it is the smallest uninteresting number. thus producing a contradiction.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

One would say that the limit of f, as x approaches a, is L, and would write it as $\lim_{x \to a} f(x) = L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$  

Infinite Limits

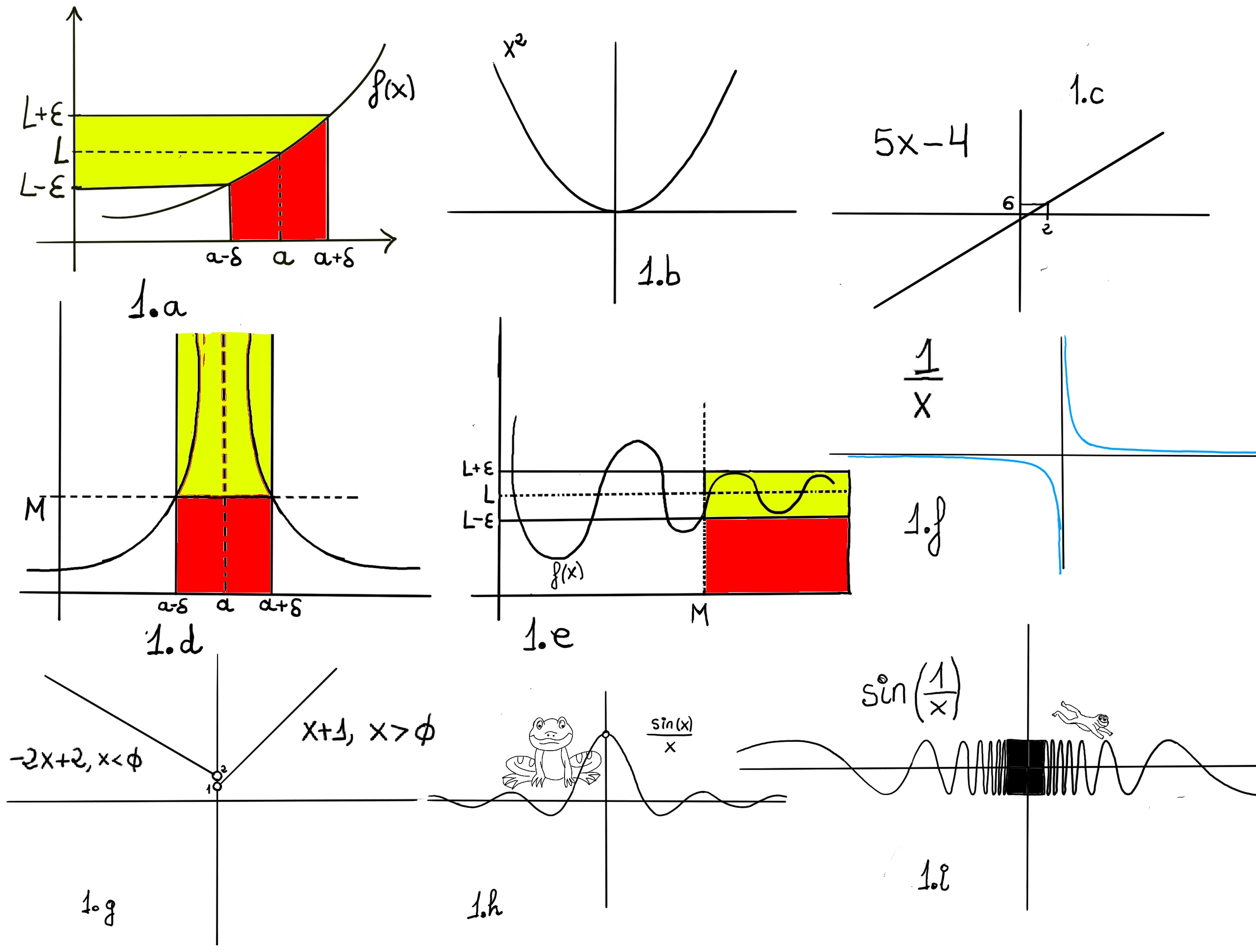
Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = \infty$ if $\forall M>0, \exists \delta>0: f(x) > M, whenever~ 0<|x-a|<\delta.$

Loosely speaking, We can make the value of f(x) arbitrary large by taking x to be arbitrary close, but never touching at x = a. -Figure 1.d.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = -\infty$ if $\forall M<0, \exists \delta>0: f(x) < M, whenever~ 0<|x-a|<\delta.$

Loosely speaking, we can make the value of f(x) arbitrary small by taking x to be sufficiently close, but never equal to a.  

Vertical Asymptotes

The vertical asymptote of a function y = f(x) is a vertical line, say x = a, when y → ∞ or y → -∞. Mathematically, if x = k is the vertical asymptote of a function y = f(x) then at least one of the following would hold true:

1. $\lim_{x \to a} f(x) = ±∞$ (or)
2. $\lim_{x \to a⁻} f(x) = ±∞$ (or)
3. $\lim_{x \to a⁺} f(x) = ±∞$

A vertical asymptote is a vertical line (x = k) marking a specific value toward which the graph of a function may approach, but will never reach, that is, the function becomes unbounded (either y tends to ∞ or -∞) but it doesn’t touch or cross the curve.

Solved examples

• $\lim_{x \to \frac{π}{2}} tan(x)$ does not exist because $\lim_{x \to \frac{π}{2}⁺} tan(x) = -∞, \lim_{x \to \frac{π}{2}⁻} tan(x) = ∞,$ (Figure i).

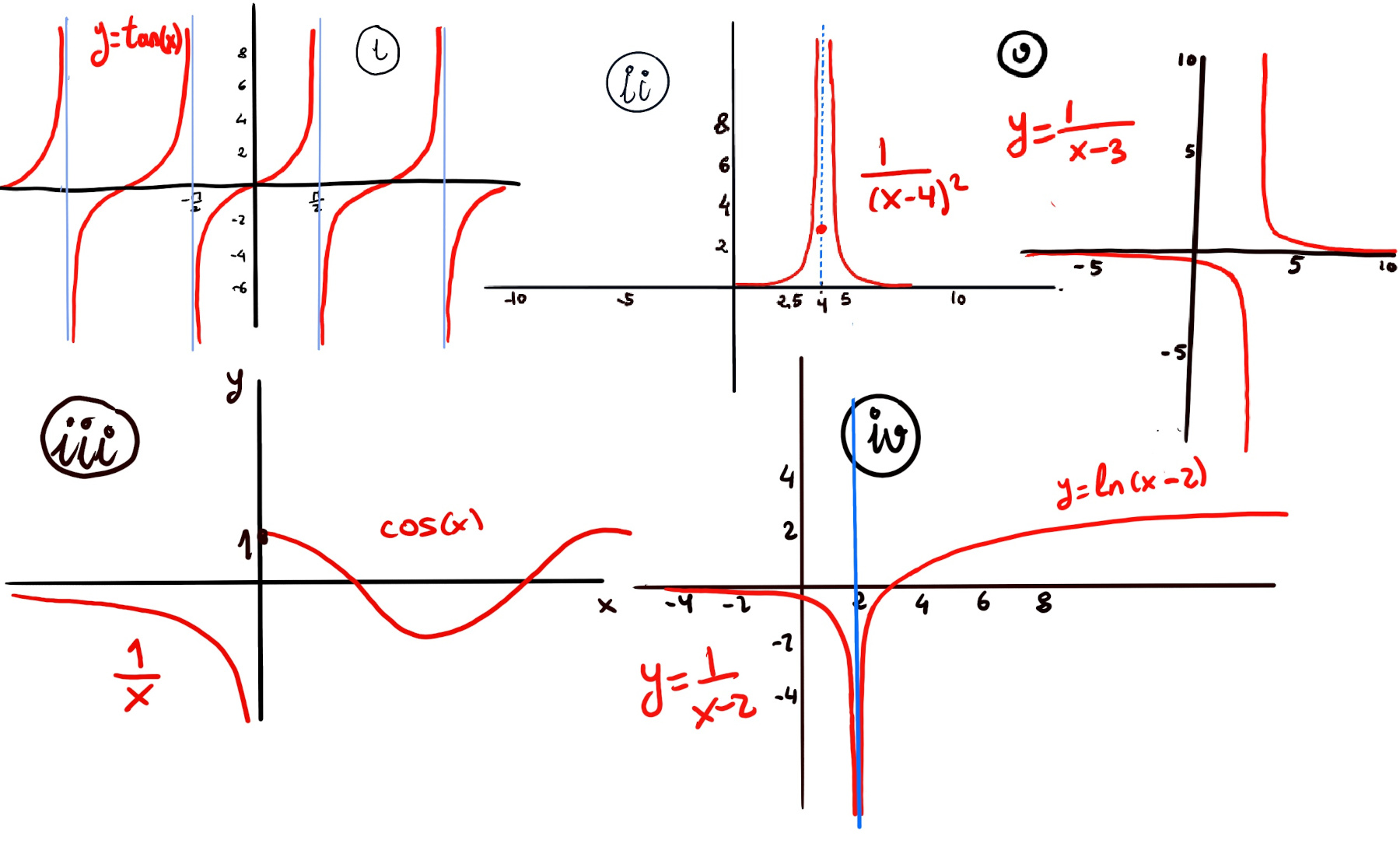
Recall that the domain of the tangent function is all real numbers except for π/2+nπ, n ∈ ℤ, because at those values the tangent function is undefined. The vertical lines through these x-values are the vertical asymptotes of the graph.

• $f(x) = \begin{cases} \frac{1}{(x-4)^2}, &x ≠ 4\\\\ 3, &x = 4 \end{cases}$ $\lim_{x \to 4} f(x) = ∞$ ≠ f(4) = 3 (Figure ii), there is a vertical asymptote at x = 4.

• $f(x) = \begin{cases} \frac{1}{x}, &x < 0\\\\ cos(x), &x ≥ 0 \end{cases}$

Approaching 0 from the left (x < 0), f(x) becomes 1/x and the function decreases to minus infinity -∞, $\lim_{x \to 0⁻} f(x) = \lim_{x \to 0⁻} \frac{1}{x} = -∞$. Approaching 0 from the right (x > 0), f(x) becomes cos(x) and we get closer and closer to 1, $\lim_{x \to 0⁺} f(x) = \lim_{x \to 0⁺} cos(x) = 1$.

Therefore, $\lim_{x \to 0} f(x)$ does not exist because the left and right limits are different, (figure 3).

• $f(x) = \begin{cases} \frac{1}{x-2}, &x < 2\\\\ ln(x-2), &x > 2 \end{cases}$

$\lim_{x \to 2⁻} f(x) = \frac{1}{x-2} = -∞, \lim_{x \to 2⁺} f(x) = ln(x-2) = -∞$, hence $\lim_{x \to -5} f(x) = -∞$ (Figure iv).

Solved examples with epsilon-delta proofs

• $\lim_{x \to 0} \frac {1}{x^{2}} = \infty$

$\forall M>0, \exists \delta>0: \frac {1}{x^{2}} > M, whenever~ 0<|x|<\delta.$

Let’s choose $\delta = \frac {1}{\sqrt M}$

$\forall M>0, \exists \delta = \frac {1}{\sqrt M}>0: \frac {1}{x^{2}} > M, whenever~ 0<|x|<\frac {1}{\sqrt M}.$

$|x|<\frac {1}{\sqrt M} ⇨ |x|^{2}<\frac {1}{M} ⇨ x^{2}<\frac {1}{M} ⇨ M <\frac{1}{x^{2}}$

• $\lim_{x \to 3⁺} \frac{1}{x-3} = ∞$ (Figure v)

$\forall M>0, \exists \delta>0: f(x)>M, whenever~ a < x < a + \delta.$

$\forall M>0, \exists \delta>0: \frac{1}{x-3}>M, whenever~ 3 < x < 3 + \delta$

$3 < x < 3 + \delta$ ⇒ x - 3 < δ ⇒[they are positive numbers because x should be relatively close to 3 and x > 3] $\frac{1}{x-3} > \frac{1}{δ}$ ⇒[Let’s choose δ = 1/M] = $\frac{1}{\frac{1}{M}} = M.$

• $\lim_{x \to 1⁺} \frac{x}{2x-2} = ∞$

$\forall M>0, \exists \delta>0: \frac{x}{2x-2}>M, whenever~ 0 < x -1 < \delta$

$0 < x -1 < \delta ⇒ \frac{1}{x-1}>\frac{1}{\delta}$[🚀]

$\frac{x}{2x-2} = \frac{x}{2}\frac{1}{x-1}>🚀\frac{x}{2}·δ >$ ⇒[0 < x -1 ⇒ x > 1 ⇒ ^x⁄₂ > ¹⁄₂] $\frac{1}{2δ} =$ [Choose δ = 1/(2M)] M

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.