
|
 |
 |

|
 |
 |
Extremely useful facts: 1 + 1 = 3, if you don’t use a condom. 1 + 1 = 0 in ℤ2. 4 x 4 = truck. 42 is the answer to the meaning of life, the universe, and everything else.
Extremely useful facts 2: 666 is Satan’s number. 7 is a highly spiritual number, it is mentioned numerous times in the Bible, often symbolizing completeness or perfection. 10 is the base of our number system because we have ten fingers. 13 is the most unlucky number in western civilization. Rule 34 is an internet concept meaning that if something exists in real life, or is made up, there will be an obscene or pornographic depiction of it, e.g., yes, there’s already erotic fanfic about the ship that got stuck in the Suez Canal: Rule 34 is alive and well.
Extremely useful facts 3: 69 is a sex position in which there is no intercourse. 420 has become a symbol for the consumption and celebration of marijuana. 10,213,223 is the only number that describes itself when you read it, that is, one zero, two ones, three twos, and two threes. Graham’s number is the highest number ever used in a mathematical proof.
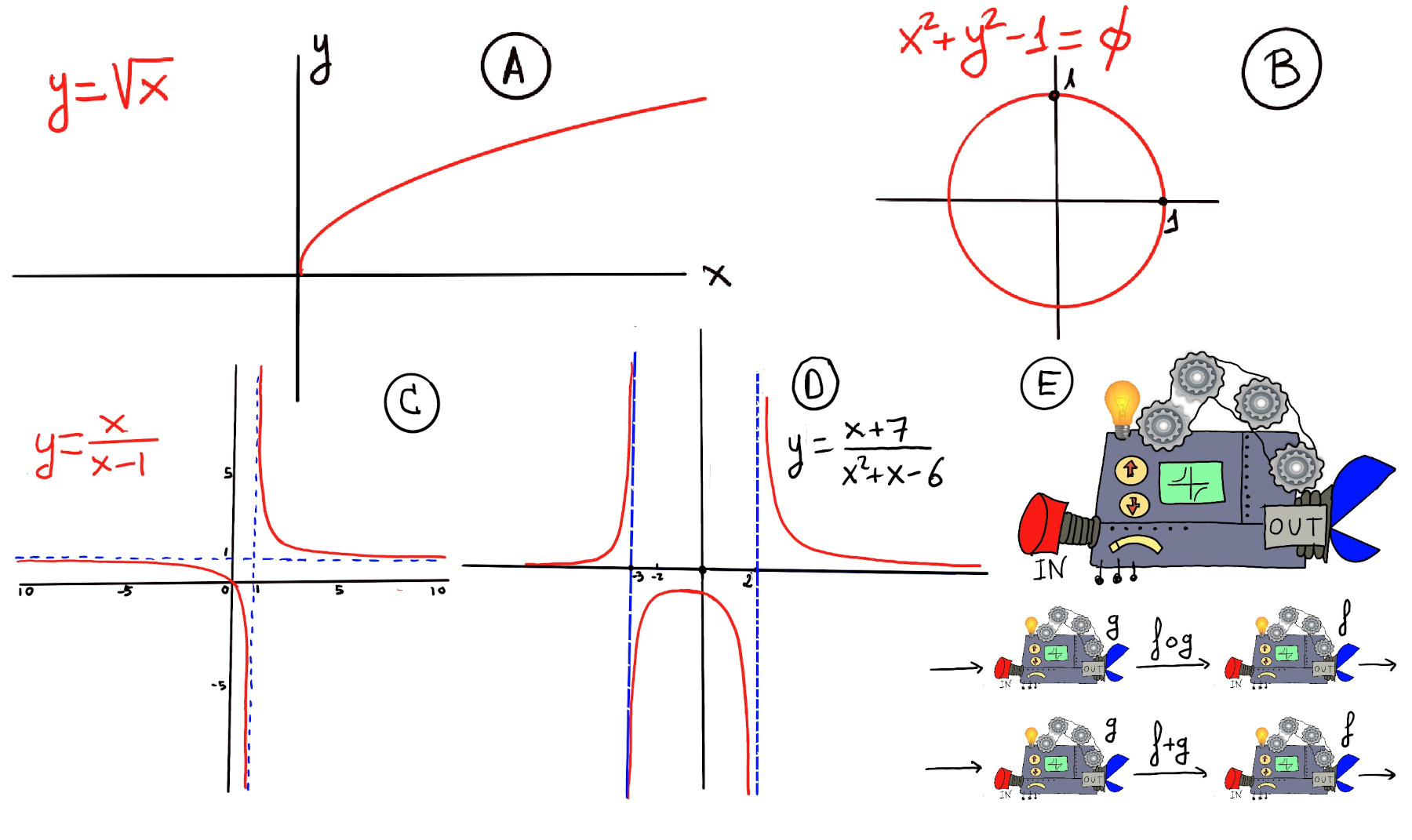
Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).
The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).
Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.
One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x) = L.$ Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-
Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if
$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$
Or
$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$
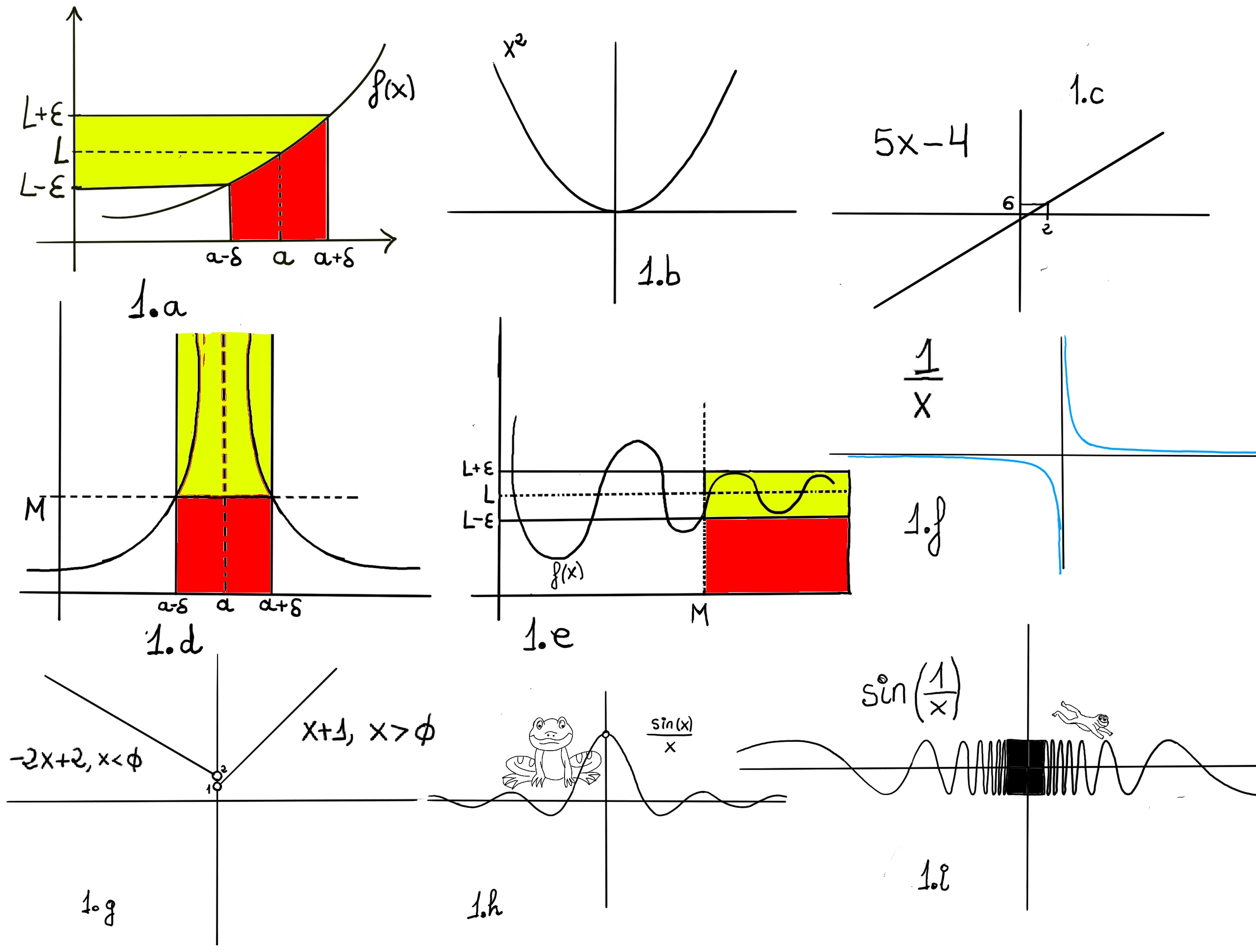
One-sided limits are a specific type of limits. They are a way to describe the behavior of a function as the input approaches a specific value from one side, either the left or the right.
Definition. A right hand limit is defined as the value L to which a function grows close as the input approaches (but never touching) some other value from the right.
Formal definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a^{+}} f(x) = L$ if
$\forall \epsilon>0, \exists \delta>0: 0 < x-a < \delta, implies~ |f(x)-L|<\epsilon$
Or
$\forall \epsilon>0, \exists \delta>0: a < x < a + \delta, implies~ |f(x)-L|<\epsilon$
Or
$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ a < x < a + \delta.$
Definition. A left hand limit is defined as the value L to which a function grows close as the input approaches (but never touching) some other value from the left.
Formal definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a^{-}} f(x) = L$ if
$\forall \epsilon>0, \exists \delta>0: a - \delta < x < a, implies~ |f(x)-L|<\epsilon$
Or
$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ a - \delta < x < a.$
If the limit of f(x) as x approaches a exists then the limits from the left and from the right both must exist and be equal. When a limit does not exist, it is possible that neither one-sided limit exists, that just one of them exists, or that both one-sided limits exist but have different values.
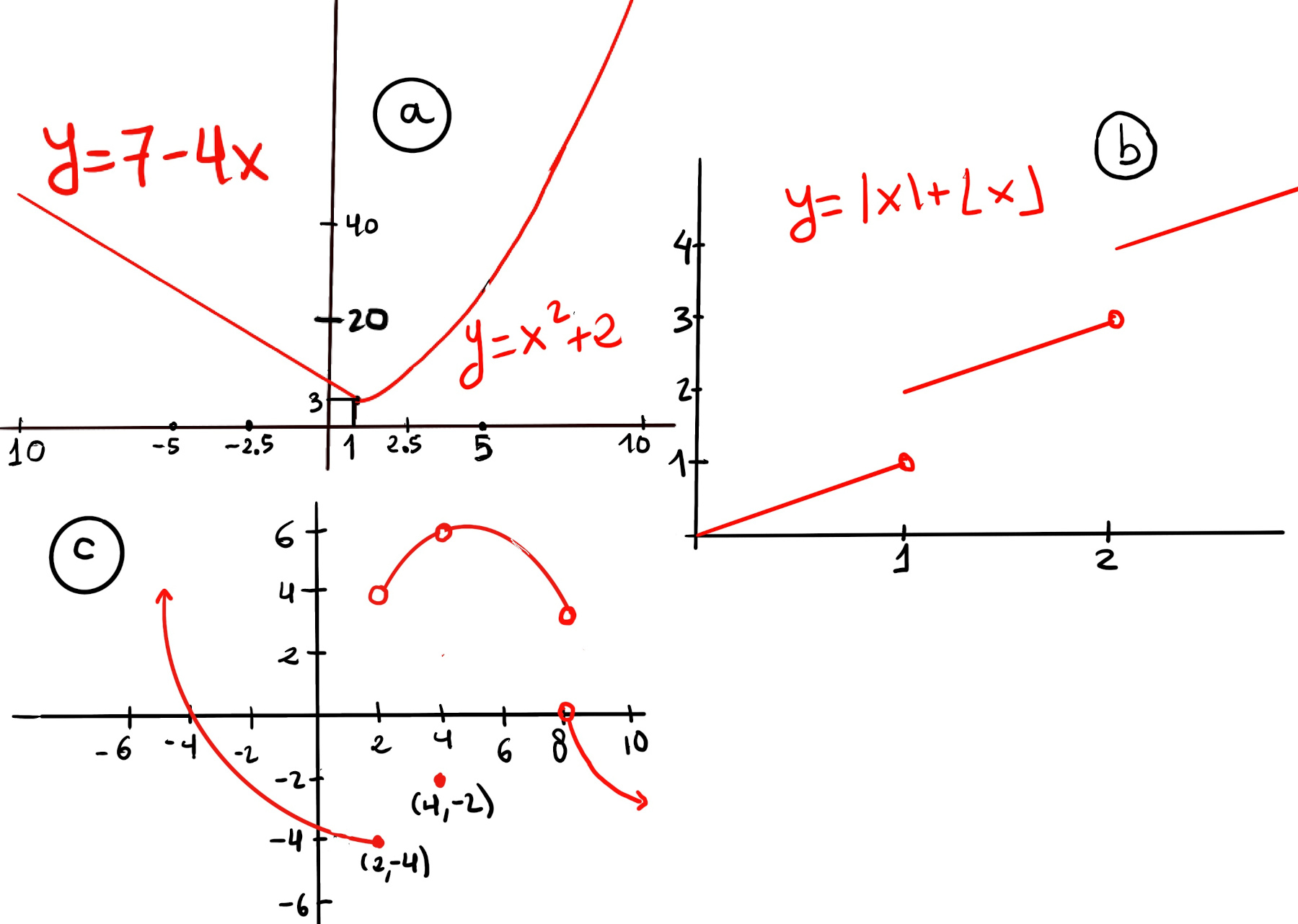 let’s calculate each of the following,
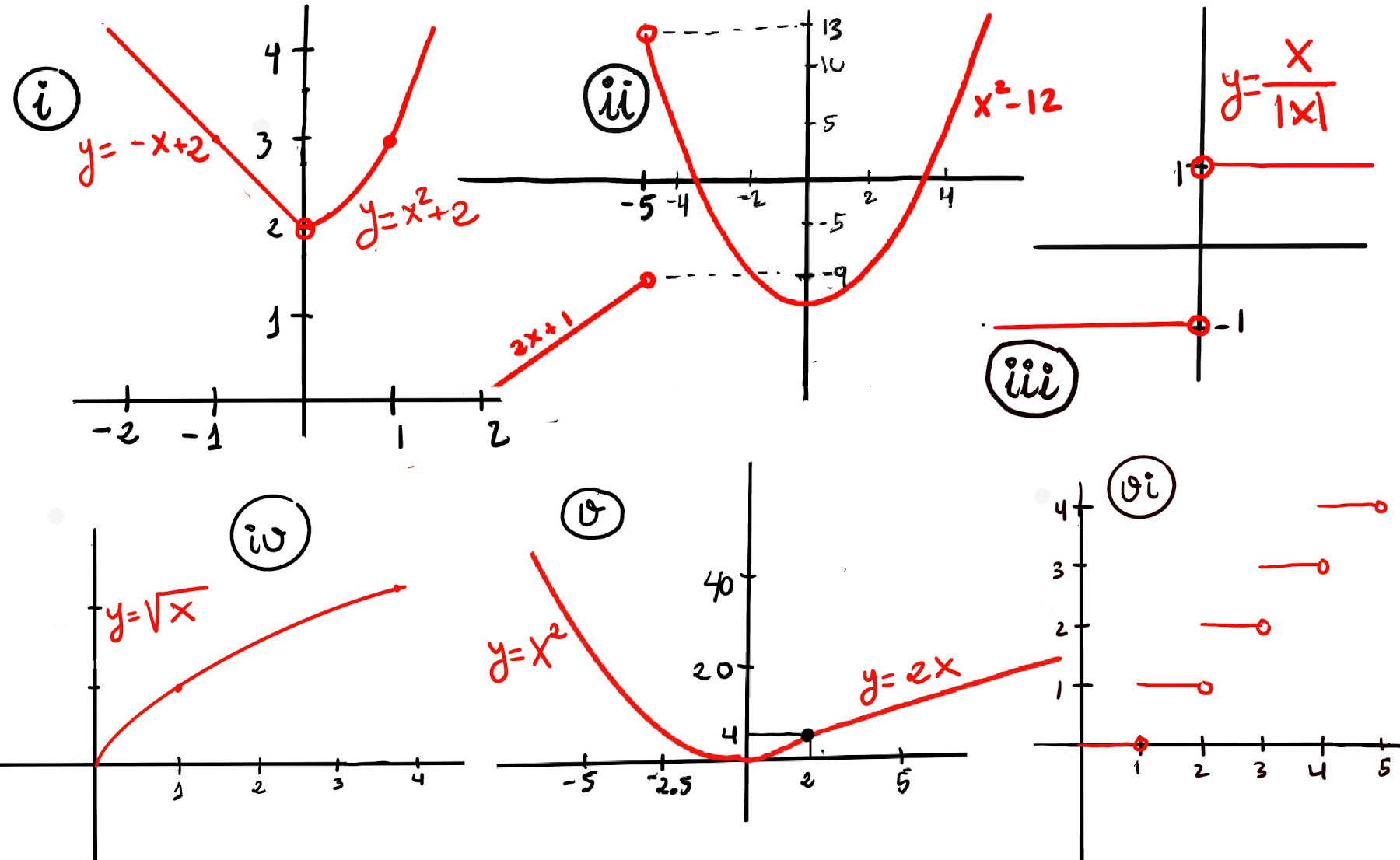
let’s calculate each of the following,Approaching 0 from the left (x < 0), f(x) becomes -x + 2 and as we get closer and closer to 2, $\lim_{x \to 0⁻} f(x) = \lim_{x \to 0⁻} -x + 2 = 2$. Approaching 0 from the right (x > 0), f(x) becomes x2 + 2 and as we get closer and closer to 2, $\lim_{x \to 0⁺} f(x) = \lim_{x \to 0⁺} x^2 + 2 = 2.$
Therefore, $\lim_{x \to 0} f(x)$ = 2, (Figure i).
Approaching 0 from the left (x < 0), f(x) becomes -2x + 2 and as we get closer and closer to 2, $\lim_{x \to 2⁻} f(x) = \lim_{x \to 2⁻} -2x + 2 = 2$. Approaching 0 from the right (x > 0), f(x) becomes x + 1 and as we get closer and closer to 1, $\lim_{x \to 2⁺} f(x) = \lim_{x \to 2⁺} x + 1 = 1$.
Therefore, $\lim_{x \to 1} f(x)$ does not exist because the left and right limits are different.
Approaching -5 from the left (x < -5), f(x) becomes 2x + 1 and as we get closer and closer to -5, $\lim_{x \to -5⁻} f(x) = \lim_{x \to -5⁻} 2x +1 = 2·-5 + 1 = -9$. Approaching -5 from the right (x > -5), f(x) becomes x2-12 and as we get closer and closer to -5, $\lim_{x \to -5⁺} f(x) = \lim_{x \to -5⁺} x^2 -12 = (-5)^2 -12 = 25 -12 = 13$.
Therefore, $\lim_{x \to -5} f(x)$ does not exist because the left and right limits are different, (Figure ii).

'''💡You can use the prompt in bing (Copilot) or chatGPT
"Write me the code in Python to plot the function
$f(x) =
\begin{cases}
2x + 1, &x < -5 \\\\
x^2 -12, &x > -5
\end{cases}$"
and then run it using an online python compile like the one provided by Online python - Codebrainy.'''
# Python code for plotting the function
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(-10, -5, 400)
x2 = np.linspace(-5, 5, 400)
y1 = 2*x1 + 1
y2 = x2**2 - 12
plt.plot(x1, y1, 'r') # 'r' specifies red color
plt.plot(x2, y2, 'r')
plt.title('Plot of the piecewise function')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()
Finding a limit by factoring is a technique to finding limits that works by canceling out common factors. It allows us to transform an indeterminate form into one that allows for direct evaluation. Notice that the limit as x approaches 0 has nothing no to do with the value of the function at x = 0.

$\lim_{x \to 2} \frac{|x-2|}{x-2}$ $\lim_{x \to 2⁻} f(x) = \lim_{x \to 2⁻} \frac{-(x-2)}{x-2} = -1, \lim_{x \to 2⁺} f(x) = \lim_{x \to 2⁺} \frac{x-2}{x-2} = 1$, hence $\lim_{x \to 2} \frac{|x-2|}{x-2}$ does not exist.
$\lim_{x \to 0⁺} \sqrt{x} = 0, f(x) = \sqrt{x}$ is only defined for x ≥ 0 (Figure iv).
$f(x) = \begin{cases} x^2, &x < 2\\\\ 2x, &x ≥ 2 \end{cases}$
$\lim_{x \to 2^{+}} f(x) = \lim_{x \to 2^{+}} 2x = 4.$ $\lim_{x \to 2^{-}} f(x) = \lim_{x \to 2^{-}} x^2 = 4.$ The overall limit as x approaches 2 exists and is equal to 4 (Figure v).

$\lim_{x \to 4⁻} f(x) = 3, \lim_{x \to 4⁺} f(x) = 4$, hence $\lim_{x \to 4} ⌊x⌋$ does not exist (Figure vi).
The greatest integer function, denoted as ⌊x⌋, gives the largest integer that is less than or equal to x
$\lim_{x \to 1⁻} f(x) = \lim_{x \to 1⁻} 7 -4x = 7 -4 = 3, \lim_{x \to 1⁺} f(x) = \lim_{x \to 1⁺} x^2 + 2 = 1 + 2 = 3 $, hence $\lim_{x \to 2} f(x) = 3$ (Figure a).

$\lim_{x \to 2} |x| + ⌊x⌋$ $\lim_{x \to 2⁻} f(x) = \lim_{x \to 2⁻} x + ⌊x⌋ = 2 + 1 = 3, \lim_{x \to 2⁺} f(x) = \lim_{x \to 2⁺} x + ⌊x⌋ = 2 + 2 = 4 $, hence $\lim_{x \to 2} |x| + ⌊x⌋$ does not exist (Figure b).
$\lim_{x \to 0} \frac{2x}{|x|+x^2}$ $\lim_{x \to 0⁻} f(x) = \lim_{x \to 0⁻} \frac{2x}{-x+x^2} = \lim_{x \to 0⁻} \frac{2}{-1+x} = -2, \lim_{x \to 0⁺} f(x) = \lim_{x \to 0⁻} \frac{2x}{x+x^2} = \lim_{x \to 0⁺} \frac{2}{1+x} = 2$, hence $\lim_{x \to 0} \frac{2x}{|x|+x^2}$ does not exist.
$\forall \epsilon>0, \exists \delta>0: |\sqrt x|<\epsilon, whenever~ 0 < x < \delta.$
Let’s choose $\delta = \epsilon^{2}$
$\forall \epsilon>0, \exists \delta>0: 0 < x < \epsilon^{2}, then~ |\sqrt x| < \sqrt{\epsilon^{2}} = \epsilon.$
$\forall \epsilon>0, \exists \delta>0: |\frac{x+|x|}{x}-2|<\epsilon, whenever~ 0 < x < \delta,$ since f is constant (in every side separately), & is arbitrary, let’s say for simplicity’s sake δ = ε.
$|\frac{x+|x|}{x}-2| =$[x > 0] $|\frac{x+x}{x}-2| = |2-2| = 0 < ε$∎
$\forall \epsilon>0, \exists \delta>0: |\frac{x+|x|}{x}|<\epsilon, whenever~ -\delta < x < 0,$ for simplicity δ = ε.
$|\frac{x+|x|}{x}| =$[x < 0] $|\frac{x-x}{x}| = 0< \epsilon$ ∎