Improper integrals type 2

Winning isn’t everything, it’s the only thing, Vince Lombardi.

Recall

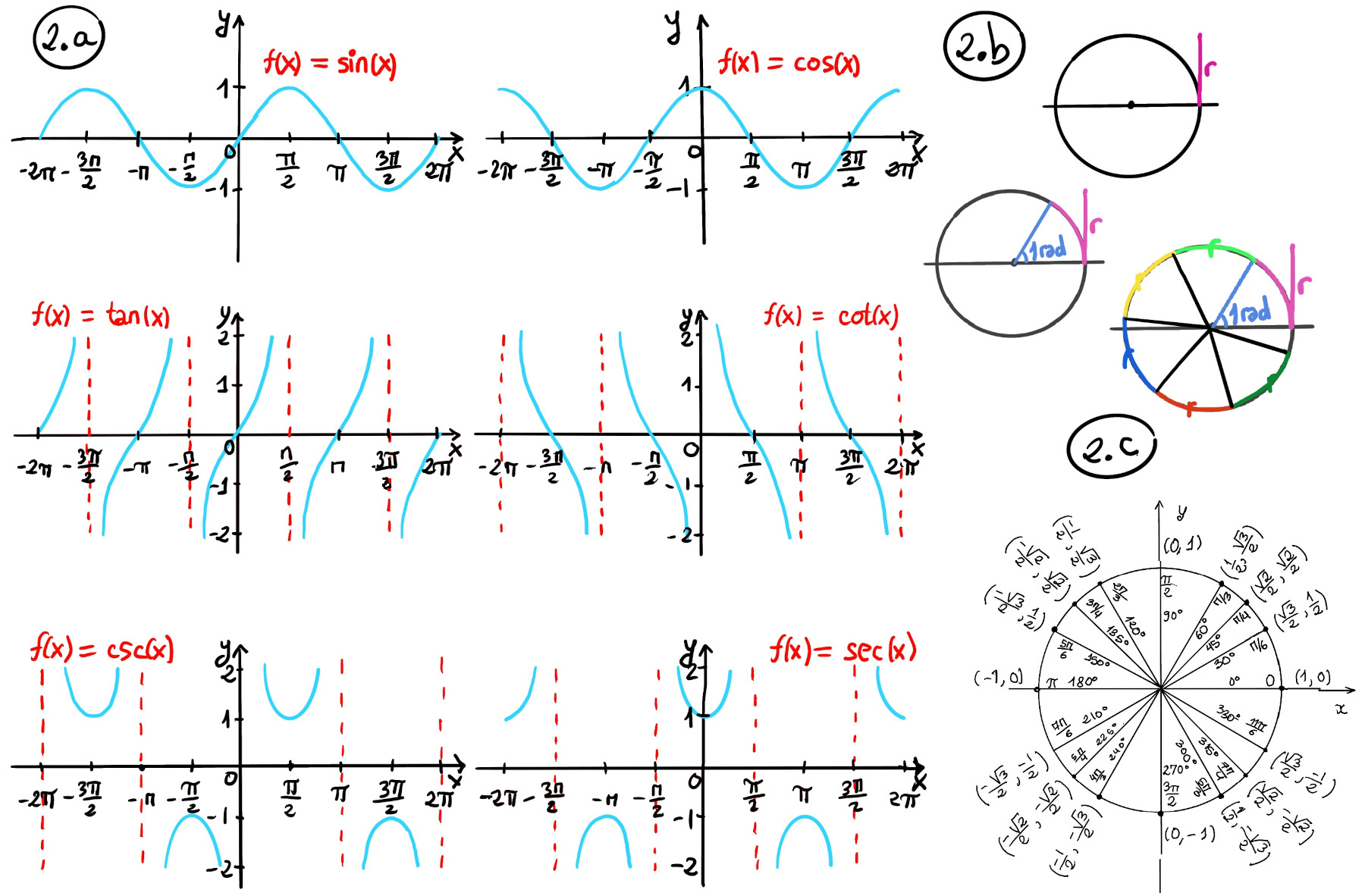
A definite integral is a mathematical concept used to find the area under a curve between two fixed limits. It is represented as $\int_{a}^{b}f(x)dx$, where a and b are the lower and upper limits, and f(x) is the integrand.

A definite integral of a function is defined as the area of the region bounded by the function's graph or curve between two points, say a and b, and the x-axis. The integral of a real-valued function f(x) on an interval [a, b] is written or expressed as $\int_{a}^{b} f(x)dx$ and it is illustrated in Figure 1.a.

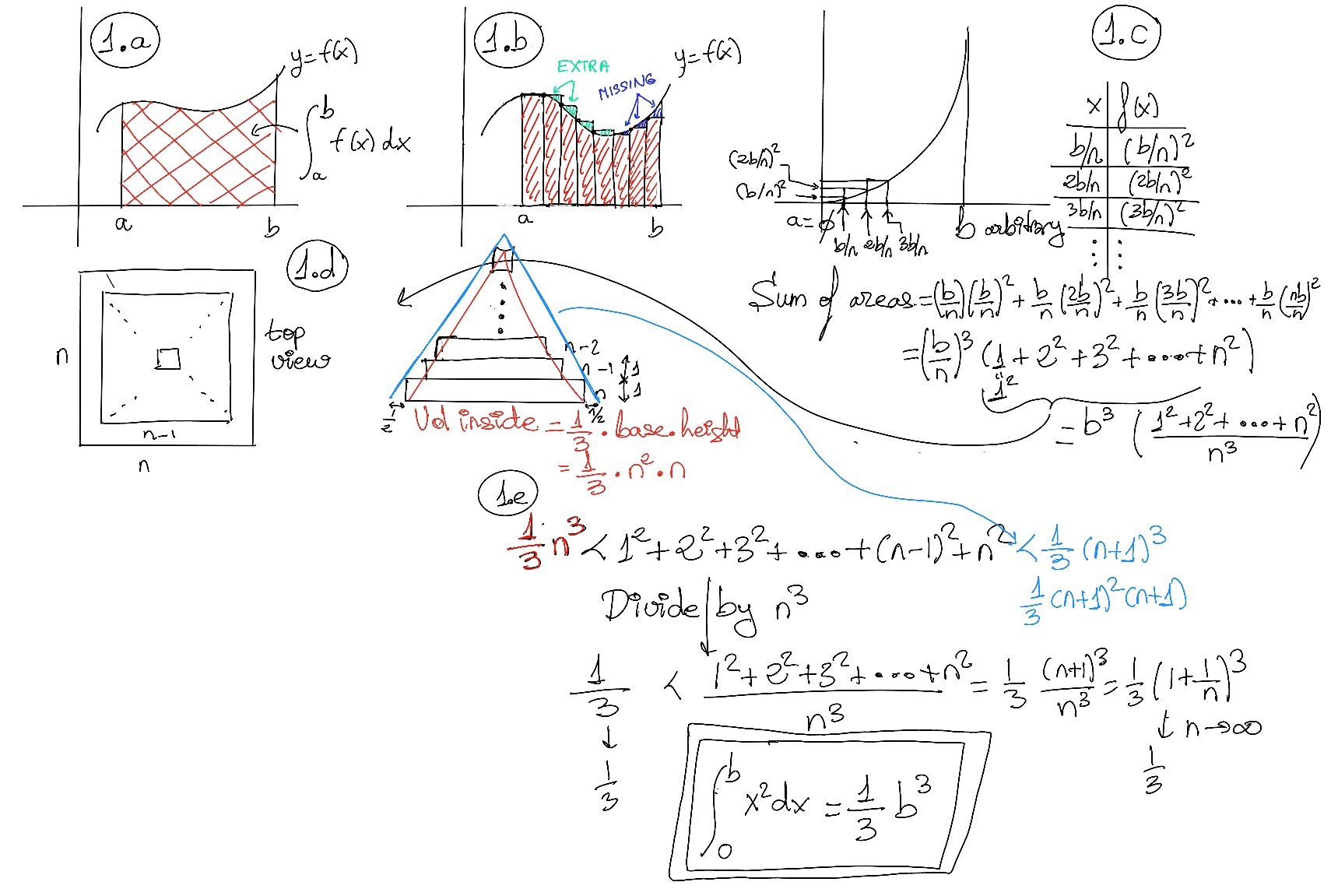
The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Definite integrals have specific limits of integration which determine the net area under the curve of the function between these limits. Improper integrals arise when the interval of integration is unbounded, that is, $\int_{a}^{∞} f(x)dx = \lim_{b \to ∞}\int_{a}^{b} f(x)dx$, or when the integrand is undefined at certain points within the interval of integration. Techniques for evaluating improper integrals involve taking limits as the integration bounds approach infinity or as singularities are approached.

Improper integrals of second type

One may be tempted to calculate $\int_{-1}^{1} \frac{dx}{x^2}=-x^{-1}\bigg|_{-1}^{1} = -2$, but this is wrong because 😞😞😞

$\int_{0}^{1} \frac{dx}{x^2}$ diverges.

An improper integral of the second kind arises when the integrand becomes unbounded or approaches infinity within the interval of integration. The integral $\int_{0}^{1} f(x)dx = \lim_{a \to 0^+} \int_{a}^{1} f(x)dx$ converges if the limit exists, and diverges if the limit does not exist (Figure 1.a.).  

Solved examples

• $\int_{0}^{1} \frac{dx}{\sqrt{x}}$. We notice that there is a vertical asymptote at x = 0, so it is an integral improper.

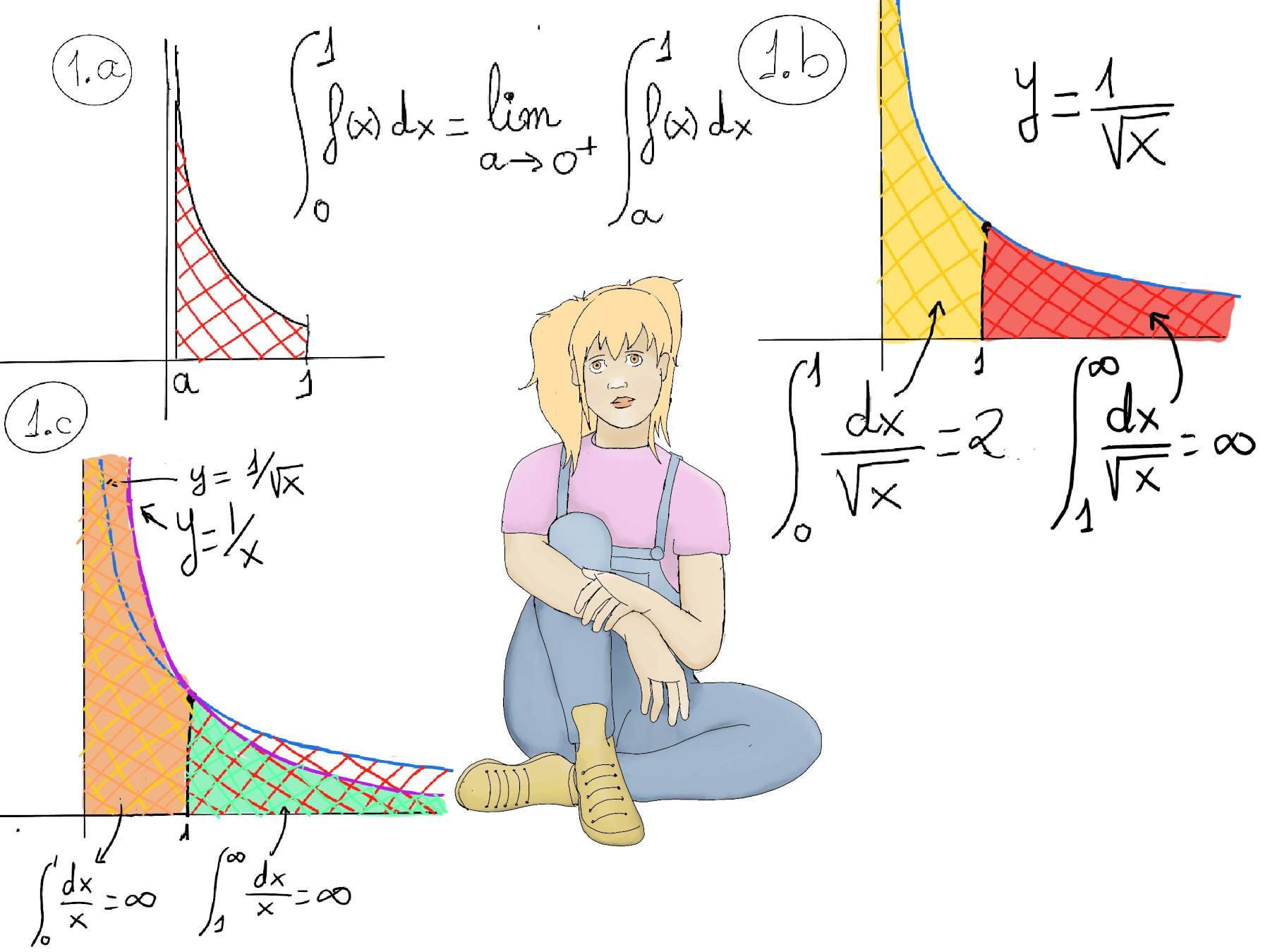
$\int_{0}^{1} x^{\frac{-1}{2}}dx = \lim_{a \to 0^+} \int_{a}^{1} x^{\frac{-1}{2}}dx = \lim_{a \to 0^+} 2x^{1/2}\bigg|_{a}^{1}$

$= \lim_{a \to 0^+} 2 -2\sqrt{a} = 2$, so the improper integral $\int_{0}^{1} \frac{dx}{\sqrt{x}}$ converges and is equal to 2 (Figure 1.b.).  

• $\int_{0}^{1} \frac{dx}{x}$. We realize that there is an infinite discontinuity at x = 0, so we need to evaluate this improper integral by taking a limit as a parameter approaches the point of discontinuity.

$\int_{0}^{1} \frac{dx}{x} = \lim_{a \to 0^+} \int_{a}^{1} \frac{dx}{x} = \lim_{a \to 0^+} lnx\bigg|_{a}^{1}$

$ = \lim_{a \to 0^+} ln1 -lna = \lim_{a \to 0^+} -lna = -(-∞) = ∞$, so this improper integral diverges (Figure 1.c.).  

The idea is quite simple, $\frac{1}{x^{1/2}} « \frac{1}{x}« \frac{1}{x^2}$ as x → 0⁺, the first integral is convergent (small enough), but the other two improper integral diverge. Similarly, $\frac{1}{x^{1/2}} » \frac{1}{x} » \frac{1}{x^2}$ as x → ∞, the only one that is convergent is the last one.

• $\int_{1⁺}^{2} \frac{1}{x^2+x-2}dx =$[The integral is improper because there is an infinite discontinuity at x = 1.] = $\lim_{a \to 1⁺} \int_{a}^{2} \frac{1}{x^2+x-2}dx = \lim_{a \to 1⁺} \int_{a}^{2} \frac{1}{(x-1)(x+2)}dx = \lim_{a \to 1⁺} \int_{a}^{2} (\frac{\frac{1}{3}}{x-1}+\frac{\frac{-1}{3}}{x+2})dx = \lim_{a \to 1⁺} \frac{1}{3}ln(x-1)-\frac{1}{3}ln(x+2) = \lim_{a \to 1⁺} \frac{1}{3} ln(\frac{x-1}{x+2})\bigg|_{a}^{2} =$

$= \lim_{a \to 1⁺} \frac{1}{3} ln(\frac{2-1}{2+2})- \frac{1}{3} ln(\frac{a-1}{a+2})= \frac{1}{3} \lim_{a \to 1⁺} ln(\frac{1}{4})- ln(\frac{a-1}{a+2}) = -(-∞) = ∞,$ so it diverges.

• $\int_{0⁺}^{1} \frac{e^{\frac{1}{x}}}{x^2}dx =$ [The integral is improper because there is an infinite discontinuity at x = 0.] $\lim_{a \to 0⁺} \int_{a}^{1} \frac{e^{\frac{1}{x}}}{x^2}dx =$ [U-Substitution u=¹⁄_x, du = ^-1⁄_x²dx, x = a ⇒ u = ¹⁄_a, x = 1⇒ u = 1] $\lim_{a \to 0⁺} \int_{\frac{1}{a}}^{1} -e^udu = \lim_{a \to 0⁺} \int_{1}^{\frac{1}{a}} e^udu = \lim_{a \to 0⁺} e^u\bigg|_{1}^{\frac{1}{a}} =$

=$ \lim_{a \to 0⁺} e^{\frac{1}{a}}-e = ∞$, it diverges.

• $\int_{1⁺}^{e} \frac{1}{x\sqrt{ln(x)}}dx =$ [The integral is improper because there is an infinite discontinuity at x = 1, i.e., √(ln(x))] $\lim_{a \to 1⁺} \int_{a}^{e} \frac{1}{x\sqrt{ln(x)}}dx =$[U-substitution, u = ln(x), du = ¹⁄_xdx, x = a ⇒ u = ln(a), x =e ⇒ u = 1] $\lim_{a \to 1⁺} \int_{ln(a)}^{1} \frac{1}{\sqrt{u}}du = \lim_{a \to 1⁺} 2\sqrt{u}\bigg|_{ln(a)}^{1} = $

$ = \lim_{a \to 1⁺} 2\sqrt{1}-2\sqrt{ln(a)} = 2.$

• $\int_{0}^{6} \frac{x}{x-2}dx = $ [The integral is improper because there is an asymptotic behaviour x approaches 2.]$\int_{0}^{2} \frac{x}{x-2}dx + \int_{2}^{6} \frac{x}{x-2}dx $

$\int_{0}^{2} \frac{x}{x-2}dx = \lim_{b \to 2⁻} \int_{0}^{b} \frac{x}{x-2}dx = \lim_{b \to 2⁻} \int_{0}^{b} \frac{x-2+2}{x-2}dx = \lim_{b \to 2⁻} \int_{0}^{b} 1dx+ \int_{0}^{b} \frac{2}{x-2}dx = \lim_{b \to 2⁻} (x+2ln|x-2|)\bigg|_{0}^{b} =$

$\lim_{b \to 2⁻} (b+2ln|b-2|-(0+2ln|-2|)) = \lim_{b \to 2⁻} (b+2ln|b-2|-2ln(2))) = -∞,$ it diverges.

• $\int_{0}^{∞} \frac{dx}{(x-3)^2} = \int_{0}^{5} \frac{dx}{(x-3)^2} + \int_{5}^{∞} \frac{dx}{(x-3)^2}$. The integral $\int_{0}^{∞} \frac{dx}{(x-3)^2}$ is improper because there is an infinite discontinuity (the function spikes up to infinity at 3 from both sides) at x = 3.

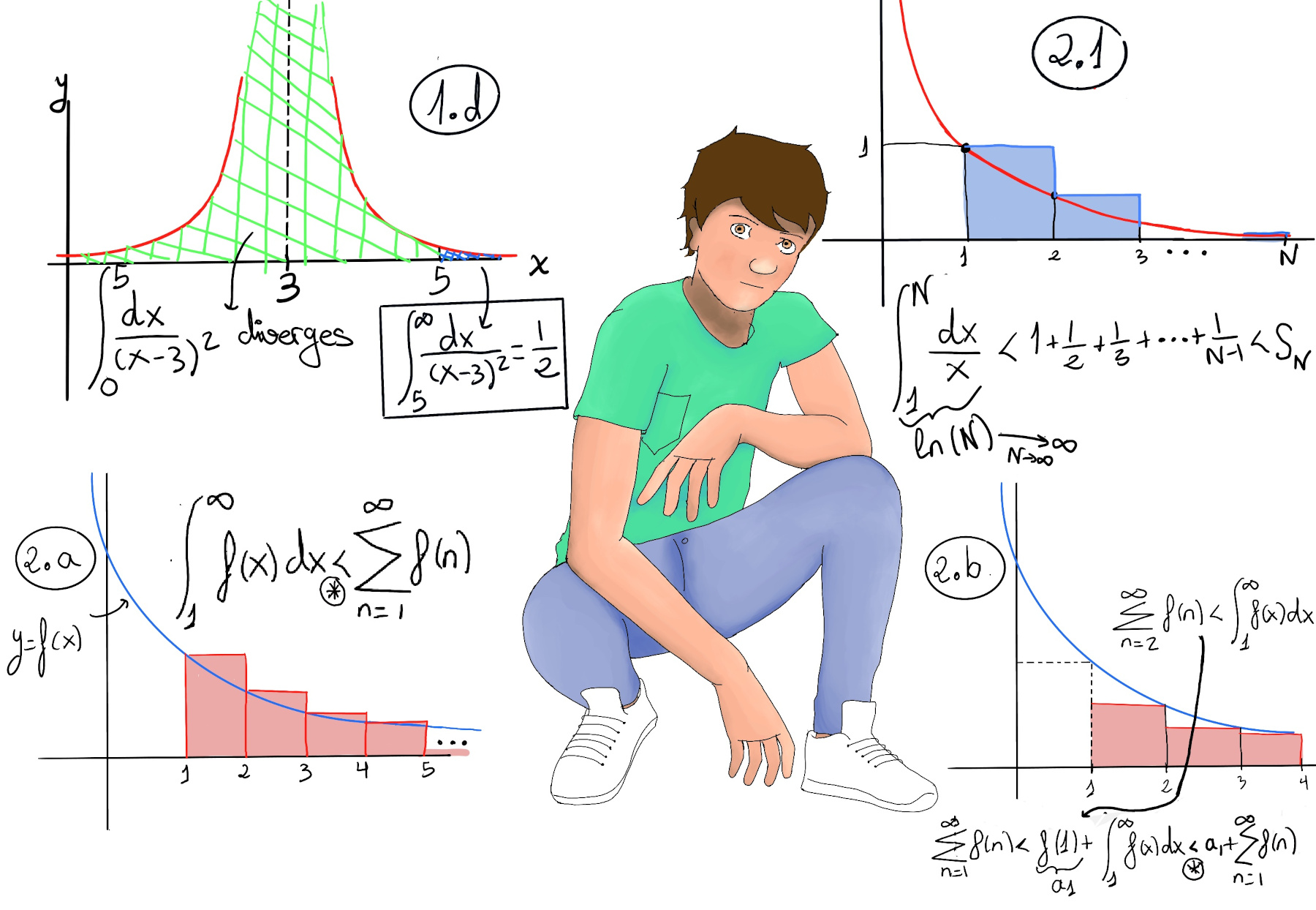
$\int_{5}^{∞} \frac{dx}{(x-3)^2} = \lim_{b \to ∞} \int_{5}^{b} \frac{dx}{(x-3)^2} = \lim_{b \to ∞} \frac{-1}{x-3}\bigg|_{5}^{b} = $

$\lim_{b \to ∞} (\frac{-1}{b-3}+\frac{1}{5-3}) = \frac{1}{2}$. Hence, $\int_{5}^{∞} \frac{dx}{(x-3)^2}$ converges, and its value is 1/2. However,

$\int_{0}^{3} \frac{dx}{(x-3)^2} = \lim_{c \to 3^-} \int_{0}^{c} \frac{dx}{(x-3)^2} = \lim_{c \to 3^-} \frac{-1}{x-3}\bigg|_{0}^{c} = $

$\lim_{c \to 3^-} (\frac{-1}{c-3}+\frac{1}{0-3}) = ∞$. So, the improper integral $\int_{0}^{3} \frac{dx}{(x-3)^2}$ diverges to infinite.

Similarly, $\int_{3}^{5} \frac{dx}{(x-3)^2} = \lim_{a \to 3^+} \int_{a}^{5} \frac{dx}{(x-3)^2} = \lim_{a \to 3^+} \frac{-1}{x-3}\bigg|_{a}^{5} = $

$\lim_{a \to 3^+} (\frac{-1}{5-3}+\frac{1}{a-3}) = ∞$. So, the improper integral $\int_{3}^{5} \frac{dx}{(x-3)^2}$ diverges to infinite ⇒ $\int_{0}^{∞} \frac{dx}{(x-3)^2}$ diverges (Figure 1.d).

• $\int_{0}^{1} x·ln(x)dx$ [Ln(x) has a vertical asymptote at x = 0, so there’s an improper integral] $\lim_{a \to 0⁺} \int_{a}^{1} x·ln(x)dx =$[Integration by parts, u = ln(x), v’ = xdx, u’=¹⁄_xdx, v = ^{x^2}⁄₂] $\lim_{a \to 0⁺} \frac{ln(x)x^2}{2}-\int_{a}^{1} \frac{x^2}{2}\frac{1}{x}dx = \lim_{a \to 0⁺} \frac{ln(x)x^2}{2}-\int_{a}^{1} \frac{x}{2}dx = \lim_{a \to 0⁺} \frac{ln(x)x^2}{2}-\frac{x^2}{4}\bigg|_{a}^{1}$

=$\lim_{a \to 0⁺} \frac{ln(1)·1}{2}-\frac{1}{4}-(\frac{ln(a)a^2}{2}-\frac{a^2}{4}) = \lim_{a \to 0⁺} -\frac{1}{4}-\frac{ln(a)a^2}{2}-\frac{a^2}{4} = -\frac{1}{4}.$

$\lim_{a \to 0⁺} \frac{ln(a)a^2}{2} = \lim_{a \to 0⁺} \frac{ln(a)}{\frac{2}{a^2}} = \lim_{a \to 0⁺} \frac{\frac{1}{a}}{\frac{-4}{a^3}} = \lim_{a \to 0⁺} \frac{-a^2}{4}=0$

• $\int_{1}^{∞} \frac{dx}{x^2+x}dx = $[$\frac{1}{x(x+1)}=\frac{A}{x}+\frac{B}{x+1} ⇒1 = A(x+1)+Bx = 1 ⇒ A = 1, B = -1$] $\int_{1}^{∞} \frac{1}{x}dx + \int_{1}^{∞} \frac{-1}{x+1}dx = \lim_{b \to ∞} \int_{1}^{b} \frac{1}{x}dx + \int_{1}^{b} \frac{-1}{x+1}dx = \lim_{b \to ∞} ln|x|-ln|x+1|\bigg|_{1}^{b}$

$=\lim_{b \to ∞} ln|b|-ln|b+1|-(ln|1|-ln|2|) = \lim_{b \to ∞} ln(\frac{b}{b+1}) +ln(2)= 0+ln(2) = ln(2),$ the integral converges.

• $\int_{2}^{∞} \frac{1}{x\sqrt{x^2-4}}dx$ =[It has both infinite interval and a discontinuous integrand] = $\int_{2}^{∞} \frac{1}{x\sqrt{4(\frac{x^2}{4}-1)}}dx = \int_{2}^{∞} \frac{1}{2x\sqrt{(\frac{x}{2})^2-1}}dx$ = [U-substitution, u = ^x⁄₂, du = ¹⁄₂dx] $\int_{2}^{∞} \frac{1}{2x\sqrt{(\frac{x}{2})^2-1}}dx = \int_{2}^{∞} \frac{1}{2u\sqrt{u^2-1}} du = \frac{1}{2} \int_{2}^{∞} \frac{1}{u\sqrt{u^2-1}} du.$

$\int \frac{1}{x\sqrt{x^2-4}}dx = \frac{1}{2} \int \frac{1}{u\sqrt{u^2-1}} du$ [Recall, $sec^{-1}(x)=\frac{1}{x\sqrt{x^2-1}}$] = $\frac{1}{2} sec^{-1}(\frac{x}{2})+C.$

$\int_{2}^{∞} \frac{1}{x\sqrt{x^2-4}}dx = \int_{2}^{3} \frac{1}{x\sqrt{x^2-4}}dx + \int_{3}^{∞} \frac{1}{x\sqrt{x^2-4}}dx$

$\int_{2}^{3} \frac{1}{x\sqrt{x^2-4}}dx = \lim_{a \to 2⁺} \int_{a}^{3} \frac{1}{x\sqrt{x^2-4}}dx = \lim_{a \to 2⁺} \frac{1}{2} sec^{-1}(\frac{x}{2})\bigg|_{a}^{3}$ =

$\lim_{a \to 2⁺} \frac{1}{2} sec^{-1}(\frac{3}{2})-\frac{1}{2} sec^{-1}(\frac{a}{2}) = \frac{1}{2} sec^{-1}(\frac{3}{2})-\frac{1}{2} sec^{-1}(1) = \frac{1}{2} sec^{-1}(\frac{3}{2}).$

$\int_{3}^{∞} \frac{1}{x\sqrt{x^2-4}}dx = \lim_{b \to ∞} \int_{3}^{b} \frac{1}{x\sqrt{x^2-4}}dx = \lim_{b \to ∞} (\frac{1}{2}sec^{-1}(\frac{b}{2})-\frac{1}{2}sec^{-1}(\frac{3}{2}))$ =[Figure 2.a, sec(x)→ ∞ when x → ^π⁄₂ ↭ sec^-1(^b⁄₂)→^π⁄₂ when ^b⁄₂→ ∞] $\frac{1}{2}·\frac{π}{2}-\frac{1}{2}sec^{-1}(\frac{3}{2}) = \frac{π}{4}-\frac{1}{2}sec^{-1}(\frac{3}{2})$, hence, $\int_{2}^{∞} \frac{1}{x\sqrt{x^2-4}}dx = \frac{1}{2} sec^{-1}(\frac{3}{2})+\frac{π}{4}-\frac{1}{2}sec^{-1}(\frac{3}{2}) $

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.