“Now, at last, I understand the general theory of relativity. Hours seem like minutes or even seconds when I am with you.” “Your futile attempt at flirting with me is hereby acknowledged,” Susanne retorted… Apocalypse, Anawim, #justtothepoint.

Recall

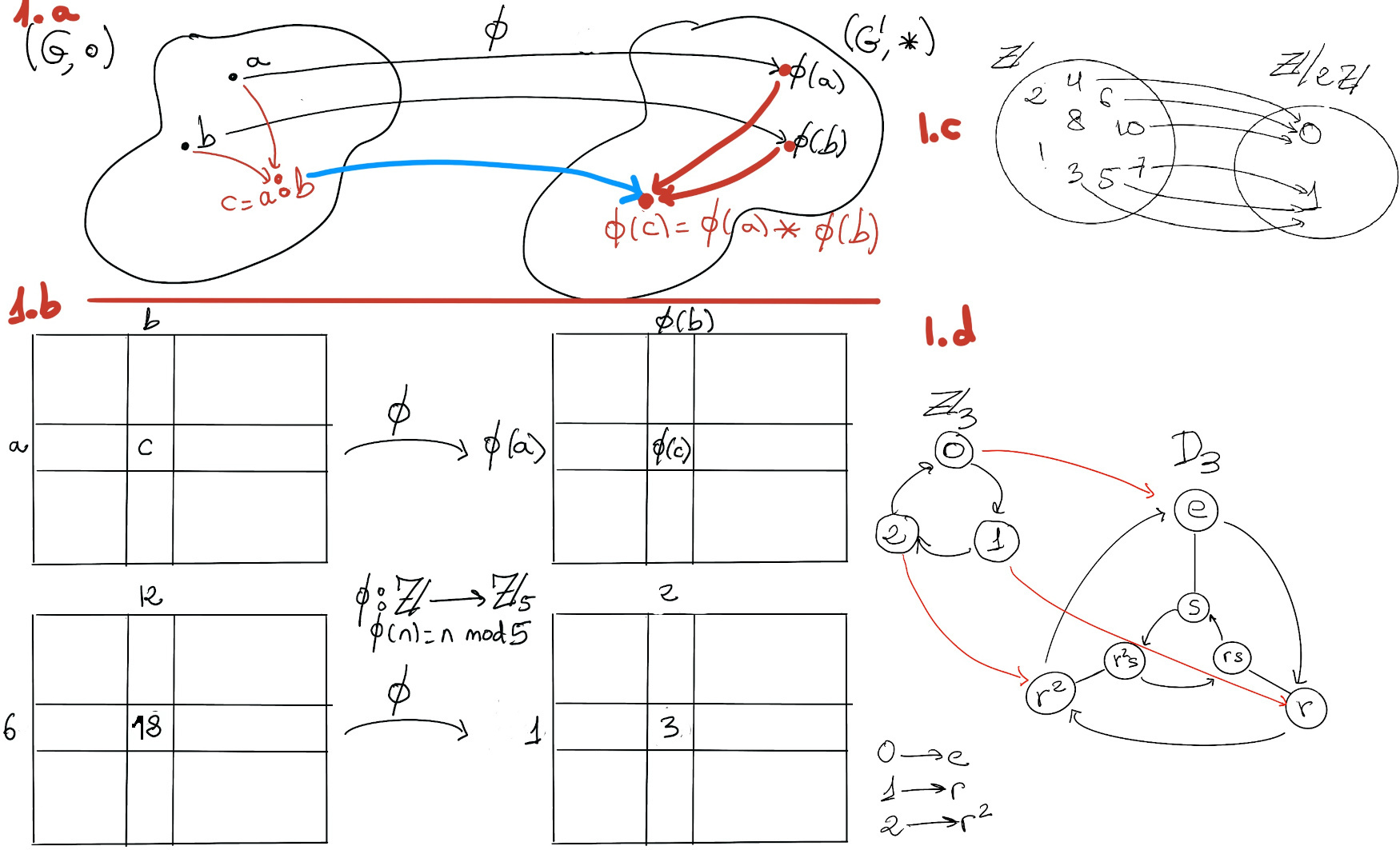
A homomorphism Φ from a group G to a group G’ is a function or a mapping from (G, ∘) to (G', *) that preserves the operations of the groups; this means a map, Φ: G → G’ between both groups that satisfies Φ(a∘b) = Φ(a)*Φ(b) for every pair a, b of elements of G, that is, ∀a, b ∈ G.

Properties (Continued)

Φ is injective if and only if its kernel is trivial. 💡The kernel of a group homomorphism measures how far off it is from being one-to-one.

⇒) Suppose Φ is injective.

∀g ∈ Ker(Φ) ⇒ Φ(g) = e’ =[Φ carries the identity] Φ(e) ⇒ [By assumption, Φ is injective] g = e ⇒ Ker(Φ) = {e}.

⇐) Suppose ker(Φ) = {e}.

∀g, g’ ∈ G: Φ(g) = Φ(g’) ⇒ Φ(g)(Φ(g’))^-1 = e’ ⇒[Φ(aⁿ) = (Φ(a))ⁿ] Φ(g)Φ(g’^-1) = e’ ⇒ Φ(g·g’^-1) = e’ ⇒[By assumption, ker(Φ) = {e}] g·g’^-1 = e ⇒ g = g’∎

Example. Let Φ: (ℝ*, ·) → (ℝ*, ·), Φ(x) = x^r, r > 0. Φ(xy) = (xy)^r = x^ry^r = Φ(x)Φ(y) ⇒ Φ is a homomorphism. Φ(x) = x^r = 1 ⇒ If r is even, Ker(Φ) = {-1, 1}. If r is odd, Ker(Φ) = {1}.

If r is even, Φ is not injective (Φ(1) = Φ(-1) = 1), and therefore it is not an isomorphism.
If r is odd, Ker(Φ) = {1} ⇒ Φ is injective. We know from Calculus that x^r is surjective using the fact that Φ is a continuos map or function, $\lim_{x \to +\infty} x^r = +\infty, \lim_{x \to -\infty} x^r = -\infty$ and applying the intermediate value theorem. Excluding zero from the domain and codomain (Φ(0) = 0, Φ is injective), Φ is still surjective, and Φ: (ℝ*, ·) → (ℝ*, ·) is an isomorphism.

If |Ker(Φ)| = n, then Φ is an n-to-1 mapping from G onto Φ(G).

This follows directly from the definition of an n-to-1 mapping (An n-to-1 mapping from G onto Φ(G) means that ∀g ∈ G, there exist n elements in G which maps to Φ(g) = g’). Recall the previously proven property (If Φ(g) = g’, Φ^-1(g’) = gKer(Φ)) and the fact that all cosets of Ker(Φ) have the same number of elements, so there are |Ker(Φ)| = n elements of G -H = Ker(Φ), all cosets of Ker(Φ) has n elements, the cardinality of the identity coset eH = H- which maps to Φ(g) = g'.

If |H| = n, then |Φ(H)| divides n.

Let’s denote Φ_H the homomorphism of Φ restricted to the elements of the subgroup H ⇒ By the previous property, Φ_H is a |Ker(Φ_H)|-to-1 mapping from H onto Φ_H(H) ⇒ |H| = n = |Φ(H)||Ker(Φ_H)| ⇒ |Φ(H)| divides n.

If K is a subgroup of G', then the preimage of K, Φ^-1(K) = {k ∈ G: Φ(k) ∈ K} is a subgroup of G.

In particular, the preimage of the identity {e’} ≤ G’ -Ker(Φ)- is a subgroup of G.

Proof.

e ∈ Φ^-1(K) because Φ(e) = e’ ∈ K (K ≤ G).

Let k₁, k₂ ∈ Φ^-1(K), k₁k₂^-1 ∈ Φ^-1(K)?

Φ(k₁k₂^-1) = Φ(k₁)Φ(k₂^-1) = Φ(k₁)(Φ(k₂))^-1 ∈ K (K ≤ G’, Φ(k₁), Φ(k₂) ∈ K) ⇒ k₁k₂^-1 ∈ Φ^-1(K) ∎

If K is a normal subgroup of G', then Φ^-1(K) = {k ∈ G: Φ(k) ∈ K} is a normal subgroup of G. In particular, the trivial subgroup is obviously normal, {e’} ◁ G’, then Φ^-1({e’}) = Ker(Φ) ◁ G. In words, kernels are normal.

Proof. (We have already proved that Φ^-1(K) ≤ G)

Suppose K ◁ G’. ∀x ∈ G, k ∈ Φ^-1(K), xkx^-1 ∈ Φ^-1(K)?

Φ(xkx^-1) = Φ(x)Φ(k)Φ(x^-1) = Φ(x)Φ(k)(Φ(x))^-1 ∈ K (By assumption, K ◁ G’ and k ∈ Φ^-1(K) ⇒ Φ(k) ∈ K) ∎

If Φ is onto and Ker(Φ) = {e}, then Φ is an isomorphism from G to G'.

If Φ is homomorphism (operation-preserving mapping), onto and Ker(Φ) = {e}, we only need to prove that is one-to-one.

We already know that if |Ker Φ| = n, then Φ is an n-to-1 mapping from G onto Φ(G) ⇒ Ker(Φ) = {e}, |Ker Φ| = 1, then Φ is a one-to-one mapping from G to G’ ∎

Examples

Let Φ: ℂ* → ℂ* be the mapping given by Φ(x) = x⁴. It is a homomorphism: Φ(xy) = (xy)⁴ = x⁴y⁴ = Φ(x)Φ(y). Ker(Φ) = {x : x⁴ = 1} = {1, -1, i, -i}.

Let’s compute all the elements that map to 2. Obviously, $Φ(\sqrt[4]{2}) = 2$ ⇒ [Φ(a) = Φ(b) if and only if aKer(Φ) = bKer(Φ)] $Φ(\sqrt[4]{2})Ker(Φ) = $ $Φ(\sqrt[4]{2})({1, -1, i, -i})$ = {$\sqrt[4]{2}, -\sqrt[4]{2}, \sqrt[4]{2}i, -\sqrt[4]{2}i$} are all elements that map to 2.

Let H = ⟨cos30° + i sin30°⟩ ⇒ [de Moivre’s theorem, (cosx + i·sinx)ⁿ = cosnx + isinnx, 12*30=360, so there are 12 elements in the unit circle] |H| = 12 ⇒ [If H is cyclic ⇒ Φ(H) is cyclic. If |H| = n ⇒ |Φ(H)| divides n] Φ(cos30° + i sin30°) =[By definition of Φ, de Moivre’s theorem] cos120° + i·sin120°, Φ(H) = ⟨cos120° + i·sin120°⟩ and Φ(H) has order 3, and obviously 3 | 12, that is, |Φ(H)| | |H|.

Let Φ: ℤ₁₂ → ℤ₁₂ be a mapping defined by Φ(x) = 3x. Φ is a homomorphism: Φ(a + b) = 3(a + b) = 3a + 3b = Φ(a) + Φ(b). ∀x ∈ Ker(Φ), 3x =_{mod 12} = 0, so Ker(Φ) = {0, 4, 8} ⇒ [If |Ker(Φ)| = n, then Φ is an n-to-1 mapping from G onto Φ(G)] Φ is a 3-to-1 mapping.

Φ(2) = 6 ⇒ [Φ^-1(a’) = {x ∈ G | Φ(x) = a’} =_{say a ∈ Φ^-1(a’)} aKer(Φ)] Φ^-1(6) =[Additive notation] 2 + Ker(Φ) = 2 + {0, 4, 8} = {2, 6, 10}. In words, 💡 Φ is a 3-to-1 mapping, so there are three distinct elements in the domain (2, 6, 10) that map to the same element in the codomain (6).

⟨2⟩ is cyclic ⇒ [If H is cyclic ⇒ Φ(H) is cyclic] ⟨Φ(2)⟩ is cyclic. Besides, ⟨Φ(2)⟩ = ⟨6⟩ = {0, 6}, and |Φ(2)| = |⟨Φ(2)⟩| = 2 divides |⟨2⟩| = 6 (Recall: If |H| = n ⇒ |Φ(H)| divides n).

Analogously ⟨1⟩ and ⟨3⟩ are cyclic, Φ(1) = 3, Φ(3) = 9, Φ^-1(3) = 1 + Ker(Φ) = 1 + {0, 4, 8} = {1, 5, 9}. Φ^-1(9) = 3 + Ker(Φ) = 3 + {0, 4, 8} = {3, 7, 11}.

Conversely, let K = {0, 6} ≤ ℤ₁₂ ⇒ [If K is a subgroup of G', then Φ^-1(K) = {k ∈ G: Φ(k) ∈ K} is a subgroup of G] Φ^-1(K) = {0, 2, 4, 6, 8, 10} ≤ ℤ₁₂

Ker(Φ) ≤ ℤ₁₂, |ℤ₁₂/Ker(Φ)| = 12/3 = 4, so ℤ₁₂ has 4 cosets, namely Ker(Φ) ∪ 1 + Ker(Φ) ∪ 2 + Ker(Φ) ∪ 3 + Ker(Φ) where Ker(Φ) = {0, 4, 8}, 1 + Ker(Φ) = {1, 5, 9}, 2 + Ker(Φ) = {2, 6, 10}, and 3 + Ker(Φ) = {3, 7, 11}.

Compute all homomorphisms from ℤ₁₂ to ℤ₇

∀n ∈ ℤ, Φ(aⁿ) = (Φ(a))ⁿ, therefore in addition notation, Φ(na) = nΦ(a). In other words, ∀n ∈ ℤ, Φ(n) = nΦ(1), that is, since there is a generator in the domain, namely 1, each homomorphism is completely specified by its image.

If |a| is finite, then |Φ(a)| divides |a| ⇒ |Φ(a)| divides |a| and also by Lagrange, 7. Besides, by Lagrange |a| needs to divide 12. Therefore, |Φ(a)| needs to divide 7 and 12 ⇒[gcd(7, 12) = 1] |Φ(a)| = 1, there is only one homomorphism, the trivial homomorphism.

Another way of seeing it. Φ(12) = Φ(0) = 0, and Φ(12) = 12·Φ(1) ≡ 0 (mod 7). Since 12 is relatively prime to 7 ⇒ Φ(1) = 0 ⇒ Φ(n) = n·Φ(1) ≡ 0 (mod 7) ∀n ∈ ℤ₁₂.

Compute all homomorphisms from ℤ₁₂ to ℤ₃₀

If |a| is finite, then |Φ(a)| divides |a| ⇒ |Φ(a)| divides |a| and also by Lagrange, 30. Besides, by Lagrange |a| needs to divide 12. Therefore, taking into consideration both constraints, |Φ(1)| = 1, 2, 3, or 6, then we can calculate all candidates for the distinct homomorphisms.

If |Φ(1)| = 4, then |Φ(1)| divides 12, but does not divide 30 (⊥).

|Φ(1)| = 6 ⇒[⟨a^k⟩=⟨a^{gcd(n, k)}⟩ and |⟨a^k⟩| = ⁿ⁄_{gcd(n, k)}, 6 = ³⁰⁄_{gcd(30, k)} = ³⁰⁄₅ ⇒ gcd(30, k) = 5] Φ(1) = 5 and 25, therefore Φ(x) = 5x mod 30 or 25 mod 30.
|Φ(1)| = 3 ⇒[⟨a^k⟩=⟨a^{gcd(n, k)}⟩ and |⟨a^k⟩| = ⁿ⁄_{gcd(n, k)}, 3 = ³⁰⁄_{gcd(30, k)} = ³⁰⁄₁₀ ⇒ gcd(30, k) = 10] Φ(1) = 10 and 20, therefore Φ(x) = 10x mod 30 or 20x mod 30.
|Φ(1)| = 2 ⇒[⟨a^k⟩=⟨a^{gcd(n, k)}⟩ and |⟨a^k⟩| = ⁿ⁄_{gcd(n, k)}, 2 = ³⁰⁄_{gcd(30, k)} = ³⁰⁄₁₅ ⇒ gcd(30, k) = 15] Φ(1) = 15, therefore Φ(x) = 15x mod 30.
|Φ(1)| = 1 ⇒[⟨a^k⟩=⟨a^{gcd(n, k)}⟩ and |⟨a^k⟩| = ⁿ⁄_{gcd(n, k)}, 1 = ³⁰⁄_{gcd(30, k)} = ³⁰⁄₃₀ ⇒ gcd(30, k) = 30 ⇒ k = 30] Φ(1) = 0, therefore Φ(x) = 0x mod 30, the trivial homomorphism.

Are there any non-trivial homomorphisms from A₄ to ℤ₂? Let Φ: A₄ → ℤ₂ be a homomorphism. Then, |Im(Φ)| ≤ ℤ₂, so there are only two choices |Im(Φ)| = 1, then Φ is the trivial homomorphism or |Im(Φ)| = 2.

Suppose for the sake of contradiction there exist non-trivial homomorphism, |Im(Φ)| = 2, ∃σ ∈ A₄: Φ(σ) = 1. We also know that Ker(Φ) ◁ A₄.

Then, Φ^-1(1) = σKer(Φ) is a coset of the kernel ⇒ Therefore, σKer(Φ) and Ker(Φ) are two left cosets, and form a partition of A₄ (Φ^-1(0) = Ker(Φ), Φ^-1(1) = σKer(Φ)). Finally, |A₄/Ker(Φ)| = 2 = 12/|Ker(Φ)| ⇒ |Ker(Φ)| = 6 ⊥ Ker(Φ) is a subgroup of A₄ of order 6, but A₄ does not have a subgroup of order 6.

Bibliography

This content is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. This post relies heavily on the following resources, specially on NPTEL-NOC IITM, Introduction to Galois Theory, Michael Penn, and Contemporary Abstract Algebra, Joseph, A. Gallian.

NPTEL-NOC IITM, Introduction to Galois Theory.
Algebra, Second Edition, by Michael Artin.
LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
Field and Galois Theory, by Patrick Morandi. Springer.
Michael Penn (Abstract Algebra), and MathMajor.
Contemporary Abstract Algebra, Joseph, A. Gallian.
Andrew Misseldine: College Algebra and Abstract Algebra.