Automorphisms. Galois extensions and groups

We shall defend our island, whatever the cost may be. We shall fight on the beaches, we shall fight on the landing-grounds, we shall fight in the fields and in the streets, we shall fight in the hills. We shall never surrender!, Winston Churchill.

Recall

A field L is said to be an extension field, denoted L/F, of a field F if F is a subfield of L, e.g., ℝ/ℚ and ℂ/ℝ. The degree of L/F, denoted [L:F] = dim_kL is the dimension of E considered as a vector space over, e.g., [ℂ : ℝ] = 2, [ℝ : ℚ] = ∞.

L/K, α is algebraic over K if α is the root of a polynomial p(x), with coefficients in the field K[x]. Otherwise, α is called transcendental. If α is algebraic, there is a smallest irreducible polynomial that it's a root of, and degree of α is the degree of such polynomial.

If X is any structured set, e.g., group, ring, field, topology, partially ordered set, etc. then an automorphism of X is a bijective function Φ: X → X such that preserves the structure of X, e.g., preserve group multiplication, addition, adjacency, etc.

Theorem. The set of all automorphisms of a field F, denoted or written as Aut(F), is a group under composition or mapping of functions. We refer to Aut(F) as the group of automorphisms of F.

 

Proof.

1. Associativity. Composition of functions is always associative, ∀α, β, τ ∈ Aut(F), ((α∘β)∘γ)(x) = (α∘β)(τ(x)) = α(β(τ(x))) = α(β∘τ(x)) = (α∘(β∘τ))(x).
2. The identity i ∈ Aut(F), i(x) = x ∀x∈ F is obviously an automorphism such that i ∘ α = α ∘ i ) = α, ∀α ∈ Aut(F).
3. ∀α ∈ Aut(F), ∃α^-1 defined as follows, α^-1(x) is the unique z ∈ F: α(z) = x.

Let’s prove that α^-1 ∈ Aut(F), ∀x, y ∈ F ∃z, t: α^-1(x) = z, α^-1(y) = t ⇒ [By definition] α(z) = x, α(t) = y ⇒ [α ∈ Aut(F)] α(z + t) = x + y ⇒ α^-1(x) + α^-1(y) = z + t = α^-1(α(z + t)) = α^-1(x + y). Mutatis mutandis, (α^-1(x))(α^-1(y)) = (α^-1(xy)), thus α^-1 ∈ Aut(F)∎

Let E be a field extension of F, then the subset of all automorphisms of E (σ: E → E) that fix F (σ(α) = α ∀α ∈ F), also called F-automorphisms of E, is a subgroup of Aut(F), denoted as Aut(E/F).

Proof:

Recall. The set of all automorphisms of a field F, denoted or written as Aut(F), is a group under composition or mapping of functions.

Since the identity fixes every element of E, in particular it fixes every element of F, id ∈ Aut(E/F).

Let σ, τ ∈ Aut(E/F), σ∘τ is an automorphism of E. It suffices to show that it fixes F ⇒ ∀α ∈ F, σ∘τ(α) = σ(τ(α)) = [τ∈Aut(E/F)] σ(α) =[σ∈Aut(E/F)] α ⇒

σ^-1 is an automorphism of E. It suffices to show that it fixes F. ∀α ∈ F, α = σ^-1(σ(α)) = [σ∈ Aut(E/F)] σ^-1(α) ⇒ σ^-1 ∈ Aut(E/F).∎

Recall Let K/F be a finite field extension. An element α ∈ K is separable over F if its irreducible polynomial over F is separable. An arbitrary polynomial over a field F is separable if its roots are distinct in an algebraic closure of F. A finite extension K/F is separable if every element of K is separable over F.

We say that E/F is a Galois extension if it is separable and normal, i.e., E is a splitting field for a polynomial or family of polynomials with no repeated roots.

If f(x) ∈ F[x] is an irreducible polynomial over a field F of characteristic zero (char(F)=0) or a finite field (|F| < ∞), then f(x) has no repeated roots and their extensions will always be separable.

Definition. Let E/F be a field extension. An automorphism of E is a ring isomorphism from E onto itself. The Galois group of E over F, written as Gal(E/F), Gal(E, F) or Gal(E : F), is the set of all field automorphisms of E which fix the base field F (i.e. take every element of F to itself). Gal(E/F) = {σ ∈ Aut(E): σ(α) = α ∀α ∈ F}.

If f(x) is a polynomial in F[x] and E is the splitting field of f(x) over F, we define the Galois group of f(x) to be G(E/F).

Example. Compute the group Gal(ℂ, ℝ).

σ ∈ Gal(ℂ, ℝ) ⇒ [By definition] σ(α) = α ∀α ∈ ℝ. Let σ(i) = j ⇒ j² = (σ(i))² = [σ ∈ Gal(ℂ, ℝ)] σ(i²) = σ(-1) = [-1 ∈ ℝ] -1 ⇒ [j² = -1] j = ± i. Therefore, there are two options:

1. j = i ⇒ ∀α ∈ ℂ, α = x +yi, σ(α) = σ(x + yi) = [σ ∈ Gal(ℂ, ℝ), σ automorphism and fixes ℝ] σ(x) + σ(y)σ(i) = x + yi ⇒ σ = id_ℂ, the identity automorphism.
2. j = -i ⇒ ∀α ∈ ℂ, α = x +yi, σ(α) = σ(x + yi) = [σ ∈ Gal(ℂ, ℝ), σ automorphism and fixes ℝ] σ(x) + σ(y)σ(i) = x - yi.

To prove that it is an automorphism, ∀α, β ∈ ℂ, α = x + yi, β = u + vi, σ(α + β) = σ((x +yi) + (u + vi)) = σ((x +u) + (y + v)i) = [By definition] (x + u) -(y +v)i = (x -yi) + (u -vi) = σ(α) + σ(β).

∀α, β ∈ ℂ, α = x + yi, β = u + vi, σ(α·β) = σ((x +yi)·(u + vi)) = σ((xu -yv) + (xv + yu)i) = [By definition] (xu - yv) -(xv +yu)i = (x -yi)·(u -vi) = σ(α)·σ(β).

Therefore, Gal(ℂ, ℝ) is the group {id_C, σ} of order 2, where σ is the complex conjugation function: x + yi → x -yi. Gal(ℂ, ℝ) ≋ ℤ₂. Futhermore, [ℂ : ℝ] = [i ∉ ℝ ( ⇒ [ℂ : ℝ] > 1), x² + 1 is the irreducible polynomial of i of degree 2] 2 = |Gal(ℂ, ℝ)|. We will demonstrate that Theorem. A finite extension K/F is Galois iff the order of the Galois group equals the degree of the extension, i.e., |Gal(K/F)| = [K : F]

Besides, α(i) = ±i, that is, σ permutes roots of f(x) = x²+1 (the irreducible polynomial of i).

Theorem. Let E be an extension of a field F and f(x) be a minimal F-polynomial of α ∈ E. Then, any automorphism σ of E leaving F fixed (σ ∈ Gal(E/F)) induces a permutation of the set of all zeros or roots of f(x) that are in E.

Proof.

Let f(x) = a₀ + a₁x + a₂x² + ··· a_nxⁿ ∈ F[x]. Suppose α ∈ E is a root of f(x), f(α) = 0.

σ ∈ Gal(E/F), 0 = [σ ∈ Gal(E/F), σ is an automorphism] σ(0) = [α is a root of f(x)] σ(f(α)) = σ(a₀ + a₁α + a₂α² + ··· a_nαⁿ) = [σ ∈ Gal(E/F), σ is automorphism that fixes F] a₀ + a₁σ(α) + a₂[σ(α)]² + ··· a_n[σ(α)]ⁿ ⇒ σ(α) is another root of f. Therefore, σ maps roots of f to roots of f, and this map must be a permutation of the roots of f(x) ∎

It is difficult for the reader to be able to grasp the far reaching consequences of this result.

Definition. Let E be an algebraic extension of a field F. We say that two elements in E (α, β ∈ E) are conjugate over F if they share the same minimal polynomial over F[x], e.g., in the field ℚ($\sqrt{2}$), $\sqrt{2}, -\sqrt{2}$ are conjugate over ℚ since they are both roots of the irreducible polynomial x² -2.

If α, β ∈ E are conjugate over F, then the map σ: F(α) → F(β) which fixes F (σ = Id_F) and send α to β, i.e., α → β can be shown to be a field isomorphism. σ can be extended to the algebraic closure of F, $σ: \bar F → \bar F$ and we will get a field automorphism that fixes the base field F, and it will permute the conjugates of the irreducible polynomial. Thus, a field automorphism induces a permutation on the conjugates of irreducible polynomials.

Example:

Let’s describe Gal($ℚ(\sqrt{2},i\sqrt{3}), ℚ$). $ℚ(\sqrt{2},i\sqrt{3})$ = {$a + b\sqrt{2}+ci\sqrt{3}+di\sqrt{6}$}. By the previous theorem, if σ ∈ Gal($ℚ(\sqrt{2},i\sqrt{3}), ℚ$) ⇒ [x² -2 = 0, x² + 3 = 0 are the irreducible polynomials of $\sqrt{2},~ and~ i\sqrt{3}$ respectively] $σ(\sqrt{2}) = ±\sqrt{2}, σ(i\sqrt{3})=±i\sqrt{3}$.

And therefore, there are only four possibilities: id, $σ(a + b\sqrt{2}+ci\sqrt{3}+di\sqrt{6}) = a - b\sqrt{2}+ci\sqrt{3}-di\sqrt{6}, τ(a + b\sqrt{2}+ci\sqrt{3}+di\sqrt{6}) = a - b\sqrt{2}-ci\sqrt{3}-di\sqrt{6}, θ(a + b\sqrt{2}+ci\sqrt{3}+di\sqrt{6}) = a - b\sqrt{2}-ci\sqrt{3}+di\sqrt{6}$.

Gal($ℚ(\sqrt{2},i\sqrt{3}), ℚ$) = {id, σ, τ, θ} ≋ K₄, the Klein 4-group, a group of four elements, each of which is self-inverse, i.e., H₁ = {id, σ}, H₂ = {id, τ}, and H₃ = {id, θ} ≤ Gal($ℚ(\sqrt{2},i\sqrt{3}), ℚ$).

Theorem. Let f(x) be a polynomial in F[x] (f(x) ∈ F[x]) and let E be the splitting field for f(x) over F. If f(x) has no repeated roots, the order of the Galois group equals the degree of the extension, |Gal(E/F)| = [E:F].

Proof. Credits: Maths StackExchange, Proof of Order of Galois Group equals Degree of Extension, @Noble Mushtak.

Let f(x) be a polynomial in F[x] with no repeated roots. Suppose E is the splitting field for f(x) over F and [E : F] = n. We are going to do induction on the degree of the extension of E/F, n.

If [E : F] = 1 ⇒ Clearly, E = F and the only possible automorphism is the identity ⇒ Gal(E/F) = {id} ⇒ |Gal(E/F)| = [E : F] = 1.

Now, let’s do strong induction on n. Assume that for all fields F, for any splitting field E of some polynomial f(x) ∈ F[x] such that [E : F] < n, |Gal(E/F)| = [E : F].

Let f(x) = p(x)q(x), where p(x) is an irreducible factor of f(x) over F[x] whose degree is r. We may assume r > 1; otherwise, f(x) splits over F and [E:F] = 1⊥

Let E be an extension field of F, f(x) ∈ F[x] has degree n ≥ 1. We say that f(x) splits in E (and E a splitting field for f(x)) if there are a, a₁, ···, a_n such that f(x) = a(a - a₁) ··· (x - a_n).

Since f(x) splits over E ⇒ p(x) splits over E and all the r roots of p(x) are in E, namely α₁, α₂, ···, α_r ⇒

[Theorem (*). Let Φ: E → F be an isomorphism of fields. Let K be an extension of E and α ∈ K be algebraic over E with minimal polynomial p(x). Suppose that L is an extension field of F such that β ∈ L is the root of the polynomial in F[x] obtained from p(x) under the image of Φ. Then, Φ extends to a unique isomorphism $\bar Φ: E(α) → F(β): \bar Φ(α)=β,~ and~ \bar Φ$ agrees with Φ on E]

∀1 ≤ i ≤ r, there is a unique isomorphism Φ_i: F(α₁) → F(α_i) such that Φ_i fixes F and Φ_i(α₁) = α_i ⇒

[Theorem. Let Φ: E → F be an isomorphism of fields and let p(x) be a non-constant polynomial in E[x] and q(x) be the corresponding polynomial under the isomorphism Φ. If K is a splitting field of p(x) and L is a splitting field of q(x), then Φ extends to an isomorphism ψ: K → L such that ψ agrees with Φ on E.]

Then, there exists an isomorphism ψ_i: E → E such that ψ_i agrees with Φ_i on F(α₁).

 

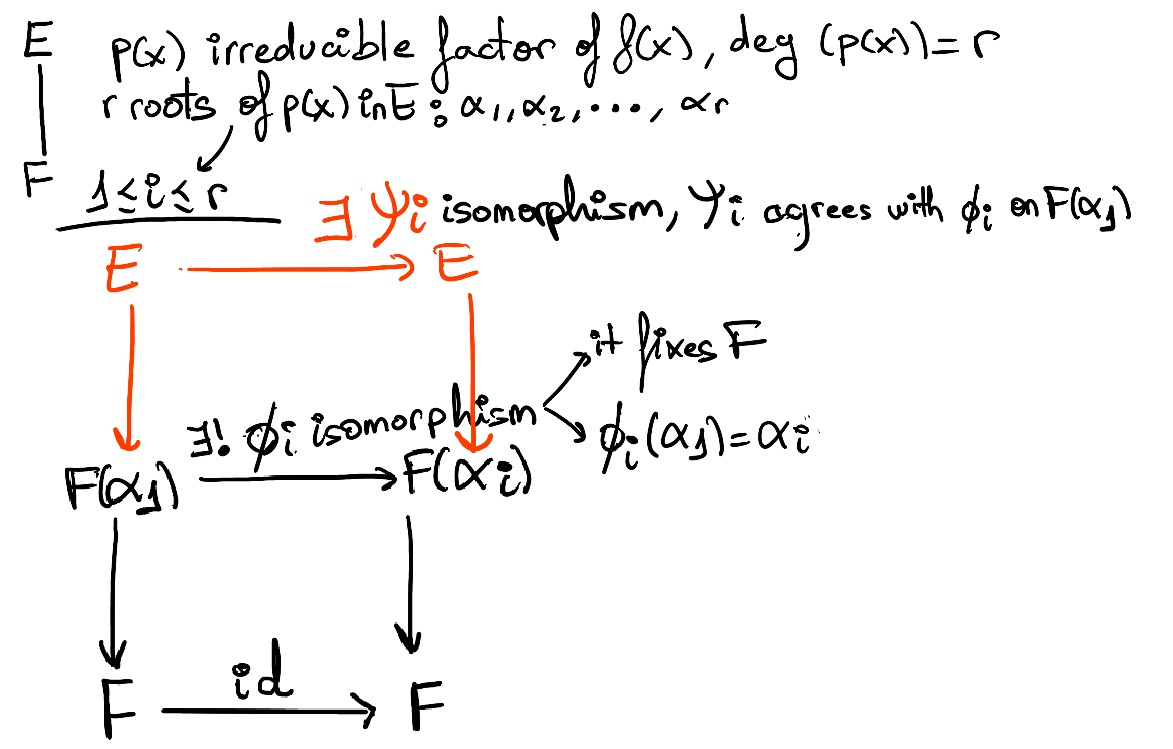
Next, take some arbitrary automorphism σ ∈ Gal(E/F) ⇒ [Let E be a field extension of F and f(x) be a polynomial in F[x]. Then, any automorphism in Gal(E/F) defines a permutation of the roots of f(x) which lie in E.] so σ(α₁) = α_i for some 1 ≤ i ≤ r, σ(F) = F(by definition σ ∈Gal(E/F)) ⇒ σ(F(α₁)) contains both F and α_i ⇒ [F(α) is the smallest subfield of E containing both F and α] σ(F(α₁)) ⊆ F(α_i)

Now, consider σ^-1(F(α_i)), clearly σ^-1(F) = F since σ fixes F. Besides, σ(α₁) = α_i ⇒ σ^-1(α_i) = α₁ ⇒ σ^-1(F(α_i)) contains both F and α₁ ⇒ σ^-1(F(α_i)) ⊆ F(α₁) ⇒ F(α_i) ⊆ σ(F(α₁)) ⇒ [We have previously demonstrated that σ(F(α₁)) ⊆ F(α_i)] F(α_i) = σ(F(α₁))

σ restricted to F(α₁) is an isomorphism from F(α₁) to F(α_i) such that σ fixes F and σ(α₁) = α_i. However, by the previous theorem (*) there is only one isomorphism which satisfies these conditions, and Φ_i, as defined below, is also an isomorphism such that Φ_i fixes F and Φ_i(α₁) = α_i ⇒ σ must agree with Φ_i on F(α₁)

Let consider ψ_i^-1σ. As it was previously stated, both σ and ψ_i agree with Φ_i on F(α₁) ⇒ ∀x ∈ F(α₁), $ψ_i^{-1}σ(x)=ψ_i^{-1}(Φ_i(x))$= [ψ_i and Φ_i agree on F(α₁) and Φ_i(F(α₁)) = F(α_i) ⇒ ψ_i^-1 and Φ_i^-1 agree on F(α_i)] $Φ_i^{-1}(Φ_i(x))=x$ ⇒ ψ_i^-1σ is an automorphism of E which fixes F(α₁), that is, ψ_i^-1σ ∈ Gal(E/F(α₁))

⇒ [If E is a finite extension of F and K is a finite extension of E, then K is a finite extension of F and [K : F] = [K : E][E : F].]

Thus [E : F] = [E : F(α₁)][F(α₁): F] ⇒ [E : F(α₁)] = ^{[E : F]}⁄_{[F(α1): F]} = n/r, thus [E : F(α₁)] < n, and the induction hypothesis applies, |Gal(E/F(α₁))| = |E : F(α₁)| = n/r, we can label these elements as θ₁, θ₂,···, θ_ⁿ⁄r.

As we have discussed earlier in this proof, ψ_i^-1σ ∈ Gal(E/F(α₁)) ⇒ ψ_i^-1σ = θ_j for some 1 ≤ j ≤ ⁿ⁄_r. In other words, for any σ ∈ G(E/F), σ = ψ_iθ_j for some i, j such that 1 ≤ i ≤ r, 1 ≤ j ≤ ⁿ⁄_r ⇒ So there are r possibilities for ψ_i and n/r for θ_j, and therefore there are r·(n/r) = n possibilities for σ ⇒ |G(E/F)| = n = [E:F] ∎