Function Fundamentals

I see in the fight club the strongest and smartest men who’ve ever lived. I see all this potential and I see squandering. God damn it, an entire generation pumping gas, waiting tables, slaves with white collars, advertising has us chasing cars and clothes, working jobs we hate so we can buy shit we don’t need. We’re the middle children of the history man, no purpose or place, we have no Great war, no Great depression, our great war is a spiritual war, our great depression is our lives, we’ve been all raised by television to believe that one day we’d all be millionaires and movie gods and rock stars, but we won’t and we’re slowly learning that fact. and we’re very very pissed off, Fight Club.

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ.

Let f be a function, a, b ∈ Domain(f). If a = b, then f(a) = f(b), e.g., f: ℚ → ℚ, f(p/q) = -p is not a function because f(¹⁄₂)=-1≠-2=f(²⁄₄), but ¹⁄₂ = ²⁄₄.

The domain of a function is the set of all inputs, in other words, it consists of all the elements for which f is defined on. The range of a function is the set of all outputs.

There are many was to represent a function:

• Verbally. It is a means of describing the relationship between inputs and outputs with words and sentences, e.g., “y is double the value of x minus five,” and “y equals x squared -4x plus 3.”
• Numerical. The function is expressed as a list of value pairs, e.g., {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10), (6, 12), (7, 14)} or {(1, 1), (4, 2), (9, 3), (16, 4), (25, 5)}.

  x	1	2	3	4	5	6	7
  f(x)	2	4	6	8	10	12	14

• A function can be represented algebraically, by using algebraic expressions or equations, e.g., 2x + 5, $\sqrt{x}, e^x, x^2-2x +4, etc.$

If a domain is not stated explicitly, the domain is the set of all numbers for which the expression makes sense and defines a real number, e.g., f(x) = x³ + 2x² + 4, Domain(f) = ℝ; g(x) = $\sqrt{x-2}$, Domain(g) = ℝ - {x ≥ 2} = [2, +∞); h(x) = $\frac{2x+3}{x^2-x}+4,$ Domain(h) = (-∞, 0) ∪ (0, 1) ∪ (1, ∞). r(x) = $\frac{\sqrt{x}}{x^2 - x},$ Domain(r) = (0, 1) ∪ (1, ∞) = {x ∈ ℝ: 0 < x < 1 or x > 1}.

• It can also be represented graphically or visually. We plot a series of inputs and outputs and connect them with a smooth line (Figure 1.a.)

• Piecewise Representation. We can create functions that behave differently based on the input (x) value. It defines different expressions for different intervals of the domain.

$f(x) = \begin{cases} x, &x ≥ 0 \\ -x, &x < 0 \end{cases}$

This is the absolute value or modulus module. The absolute |x| of a real number x is the non-negative value of x without regard to its sign. It is the distance of the number from zero on a number line.

$f(x) = \begin{cases} x + 1, &x > 0 \\ -2x + 2, &x < 0 \end{cases}$

• Recursive Representation defines values of the functions for some inputs in terms of the values of the same function for other inputs.

The Fibonacci numbers are the numbers in the following sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, ···. By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two. In mathematical terms, F(n)= F(n-1) + F(n-2) where F(0) = 1 and F(1) = 1 (Case base).

The factorial function of a whole number, written as n!, is found by multiplying n by all the whole numbers less than it, e.g., 5! = 5·4·3·2·1 = 120, 4! = 4·3·2·1 = 24. In can also be defined recursively as n! = n·(n-1)!.

• Parametric representation. A function y = f(x) is represented via a third variable, say t, which is known as the parameter, e.g., x = 4t, y = 2t² for -1 ≤ t ≤ 1. It is often possible to convert a parametric representation of a function into the more usual form by combining the two expressions to eliminate the parameter, y = 2t² =[t = ^x⁄₄] $2(\frac{x}{4})^2=\frac{2x^2}{16}=\frac{x^2}{8}$ (Figure 2.a).

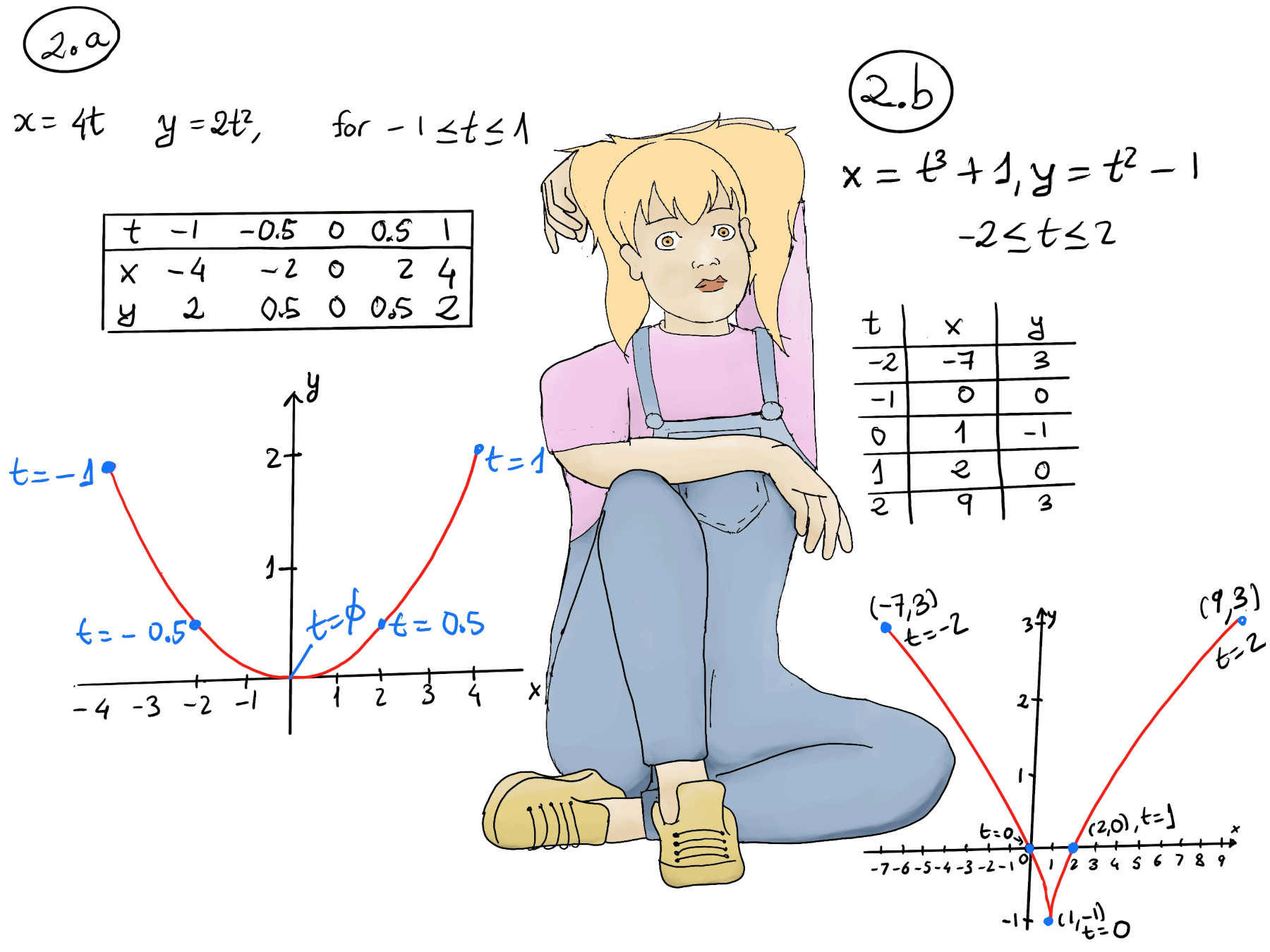
Another example is x = t³ + 1, y = t² −1, −2 ≤ t ≤ 2 (Figure 2.b.). We can also eliminate the parameter t, y = t² −1 =[t = (x-1)^1/3] = $(x-1)^{2/3}-1.$

• Integral representation. We can define a function using an integral. It is an integral expression describing the value of a function at a certain point via integration of a given function over a domain, e.g., f(x) = $\int_{0}^{x} e^{-t^2}dt,$ f(n) = $\int_{0}^{∞} x^ne^{-n}dx$ (This is the factorial function).

• Series representation. It expresses the function as an infinite series, e.g., $e^x = \sum_{n=0}^\infty \frac{x!}{n!}$, cos(x) = $\sum_{n=0}^\infty \frac{(-1)^nx^{2n}}{(2n)!}$, sin(x) = $\sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}$.

Evaluation of a function

Evaluating a function means finding the value of f(x) that corresponds to a given value of x. Examples:

• f(x) = $x^2-2x +4$, f(2) = 4 - 4 + 4 = 4, f(0) = 4, f(1) = 1 -2 +4 = 3.

• x	1	2	3	4	5	6	7
  f(x)	2	4	6	8	10	12	14

1. Domain(f) = {1, 2, 3, 4, 5, 6, 7}. Range(f) = {2, 4, 6, 8, 10, 12, 14}
2. f(5) = 10, f(2) = 4, f(3) = 6, but f(9) is undefined.
3. Solve the equation f(x) = 12. The solution is x = 6. Solve the equation f(x) = 5. The solution does not exist.
4. Solve the inequality f(x) > 10. The solution is x = 6 or 7.

The Vertical Line Test

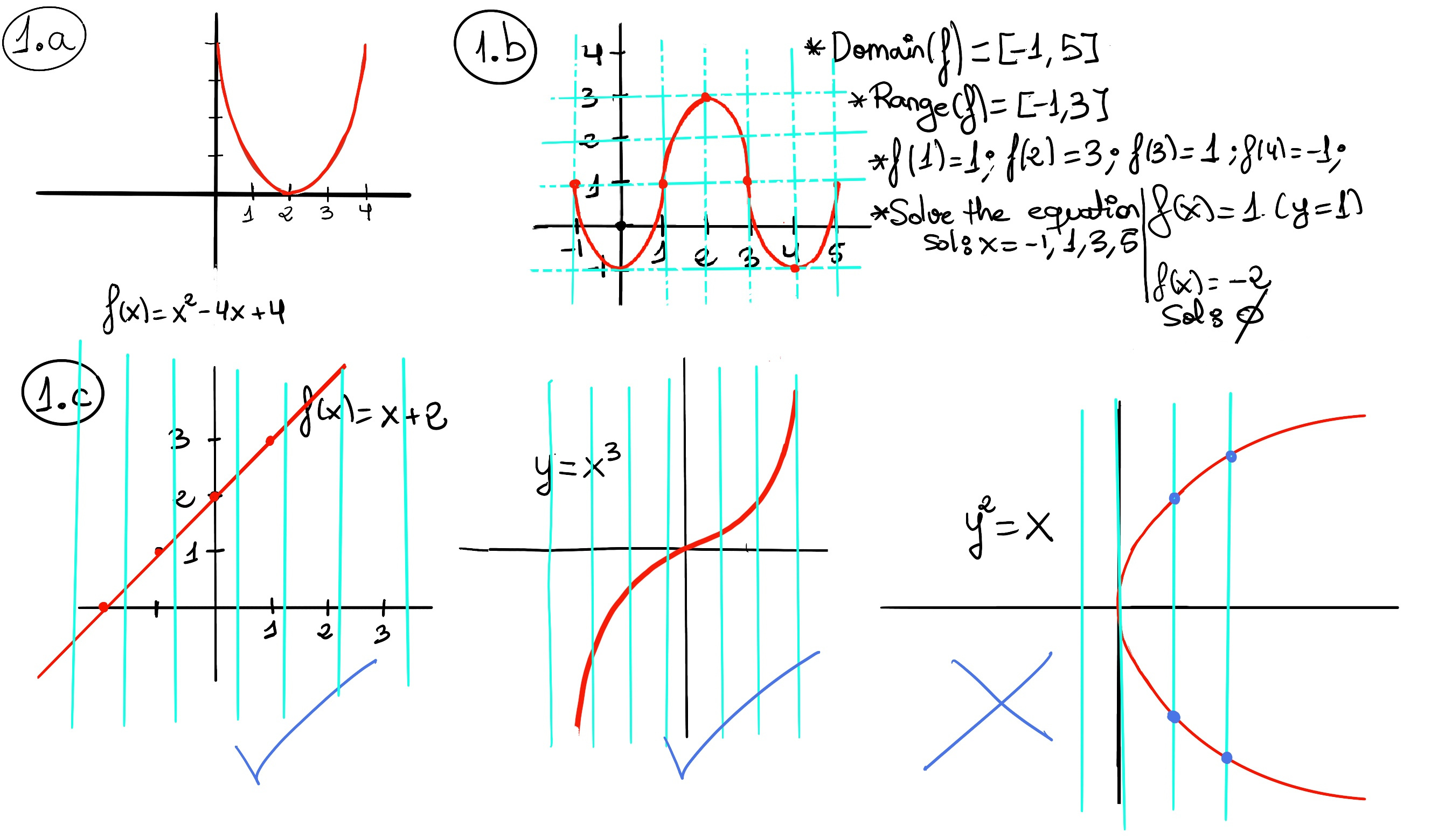
The vertical line test is a graphical method of determining whether a curve represents the graph of a function or not by visually examining the number of intersections of the curve with vertical lines. A vertical line needs to intersect the graph of a function at most at one point for it to represent a function.

Example: f(x) = x + 2, y = x³ are functions, but y² = x ↭ y = $±\sqrt{x}$ is not a function (e.g., x = 4, y = ±2) -Figure 1.c-. The circle x² + y² = 9 is not a circle either.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.