Fermat's Theorem

We shall go on to the end, we shall fight in France, we shall fight on the seas and oceans, we shall fight with growing confidence and growing strength in the air, we shall defend our island, whatever the cost may be. [···] We shall fight on the beaches, we shall fight on the landing grounds, we shall fight in the fields and in the streets, we shall fight in the hills; we shall never surrender, Winston Churchill.

Recall

The maxima and minima of a function, known collectively as extrema are the largest and smallest value of the function, either within a given range (the local or relative extrema), or on the entire domain (absolute extrema).

Notice that the definition of absolute extrema entails that an absolute extremum, unlike a relative extremum, may fall on an endpoint.

A critical point is a point in the domain of the function where the function is either not differentiable or the derivative is equal to zero. The value of the function at a critical point is called a critical value.

The squeeze or sandwich theorem. If a function f lies between two functions g and h, and the limits of each of them at a particular point are equal to L, then the limit of f at that particular point is also equal to L.

Formal definition. Let f, g, and h be functions defined on an interval I that contains x = a, except possibly at x = a. Suppose that for every x in I not equal to a, we have g(x) ≤ f(x) ≤ h(x), and also suppose that $\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L.$ Then, $\lim_{x \to a} f(x) = L.$

Extreme Value Theorem. If f is a continuous function on an interval [a,b], then f has both maximum and minimum values on [a,b]. It states that if a function is continuous on a closed bounded interval, then the function must have a maximum and a minimum on the interval (Figure 1.f.), you can see the proof at Extreme Value Theorem.

Fermat’s Theorem

Fermat’s Theorem. If a function ƒ(x) is defined on the interval (a, b), it has a local extremum (relative extrema) on the interval at x = c, and ƒ′(c) exists, then x = c is a critical point of f(x) and f'(c) = 0 (Figure 1.a.)

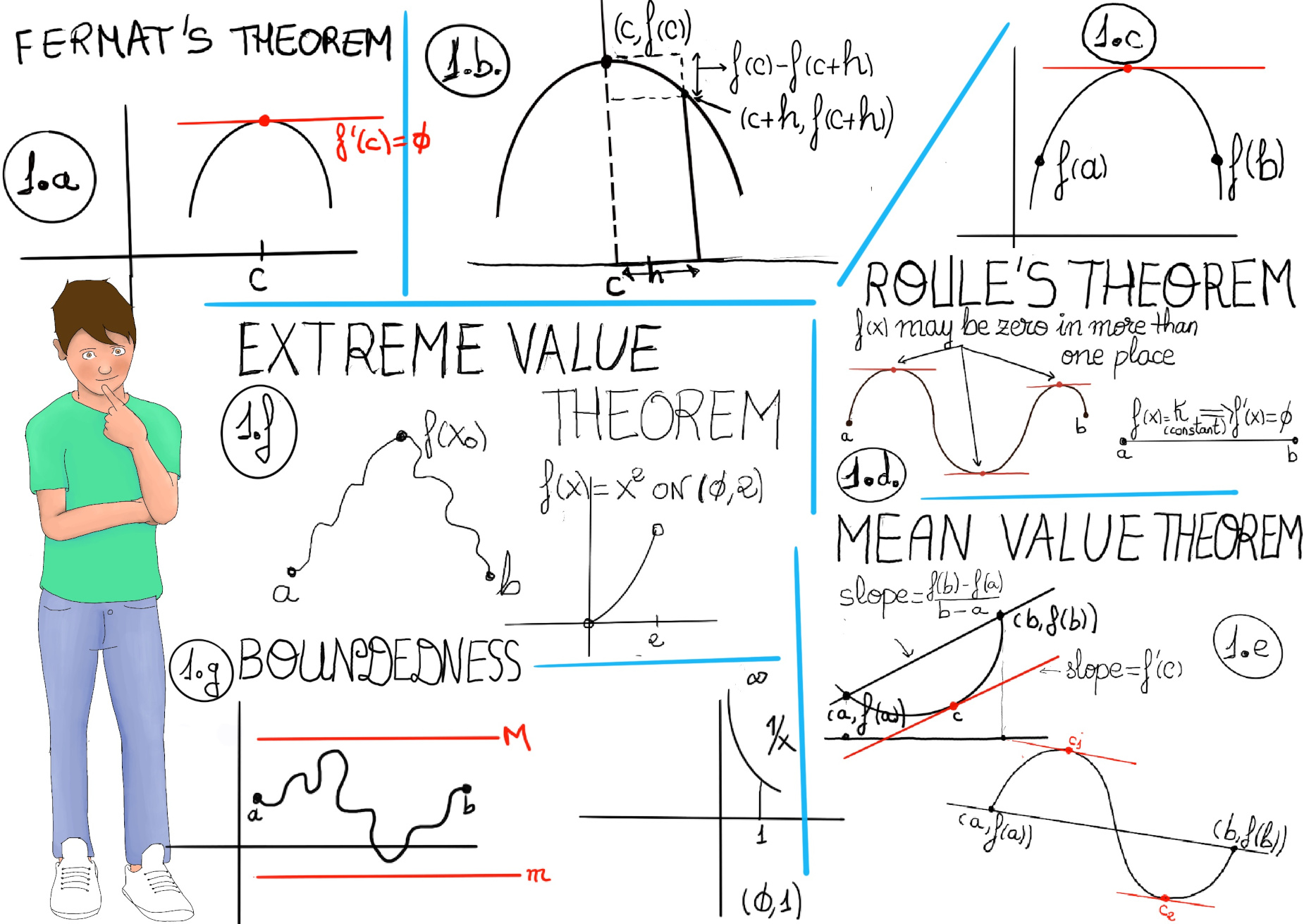
Proof:

Let’s assume that f(x) has a relative maximum on the interval at x = c. The proof for a relative minimum is pretty identical. In other words, there is no loss of generality.

$f’(c)=\lim_{h \to 0}=\frac{f(c+h)-f(c)}{h}$=[By assumption, the limit exists] $\lim_{h \to 0^{+}}\frac{f(c+h)-f(c)}{h}≤0$ because we are dividing f(c+h)-f(c) ≤ 0 -c is a relative maximum. f(c) ≥ f(c+h)- and h>0 (Figure 1.b.). Therefore, f’(c) ≤ 0.

$f’(c)=\lim_{h \to 0}=\frac{f(c+h)-f(c)}{h}=\lim_{h \to 0^{-}}\frac{f(c+h)-f(c)}{h}≥0$ because we are dividing f(c+h)-f(c) ≤ 0 -c is a relative maximum- and h<0. Therefore, f’(c) ≥ 0. We have already shown that f’(c) ≤ 0 and f’(c) ≥ 0, so f’(c) = 0 ∎

• The converse of this theorem is not true. We can have a critical point c such that f(c) is not a local maximum or minimum, e.g., f(x) = x³ (Figure i) has a critical point at x = 0 (f’(x) = 3x², f’(0) = 0), yet (0, f(0)) is neither a local maximum nor minimum.

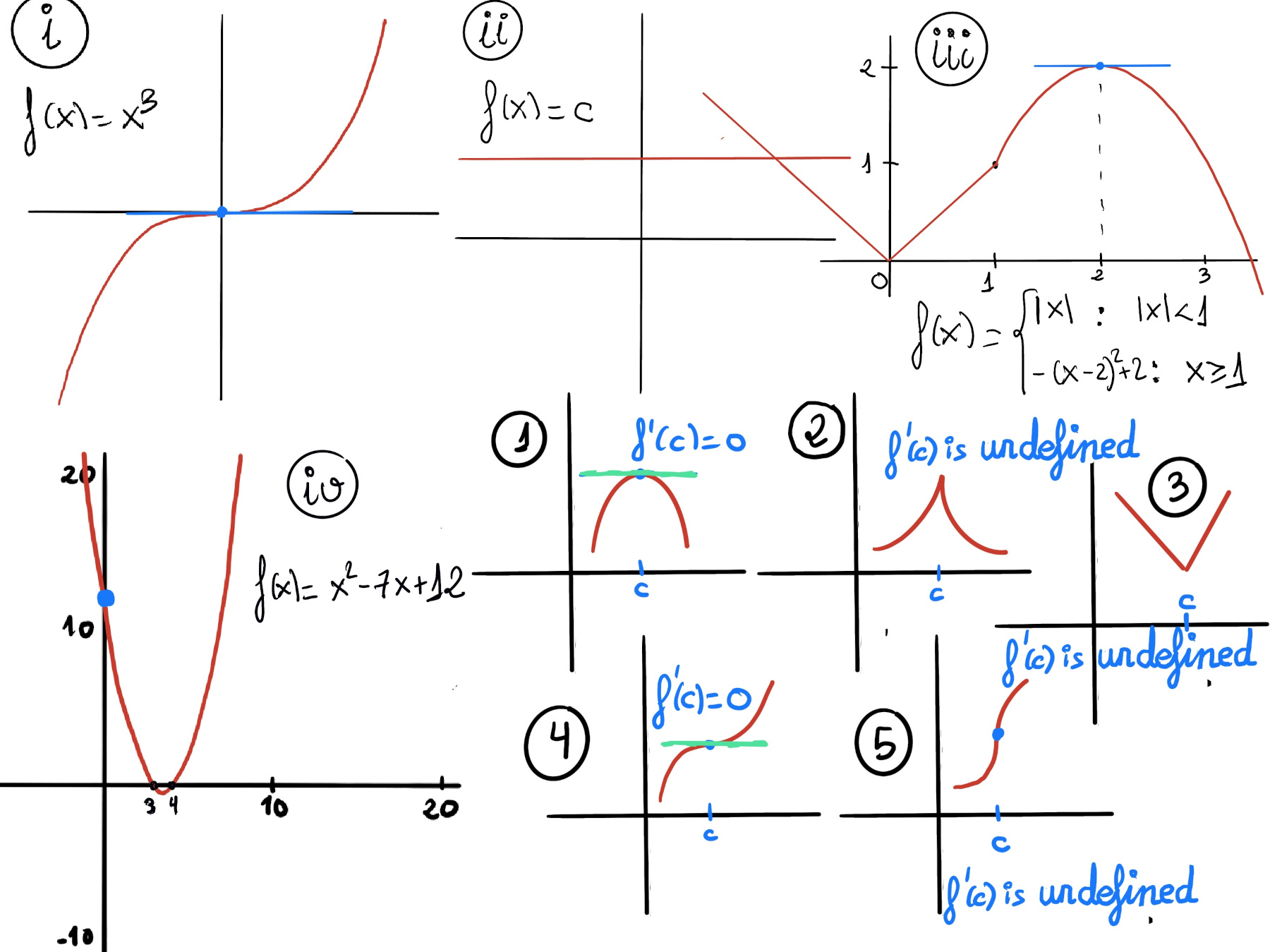
• Extreme cases. Constant functions, f(x) = c (Figure ii), are such that every point is critical (f’(x) = 0 ∀x ∈ ℝ), global and local maximum and minimum, and y = c is both the minimum and maximum value.

• Consider the following piece-wise function, $f(x) = \begin{cases} |x|, &x < 1 \\ -(x - 2)^2 + 2, &x ≥ 1 \end{cases}$

$f’(x) = \begin{cases} -1, &x < 0 \\ 1, &0 < x < 1 \\ 2(x -2), &1 < x \end{cases}$

f has a local minimum at x = 0 and a local maximum at x = 2 and three critical points, namely 0 and 1 (because f’(0) and f’(1) are not defined), and 2 (f’(x) = 0 ↭ 2·(x-2) = 0↭ x = 2). Since f’(2) exists, we already knew that f’(2) = 0 (Figure iii).

• Find the maximum value of the function f(x) = x² -7x + 12 on the interval [0, 1].

1. f is continuous and differentiable, f’(x) = 2x -7 = 0 ↭ x = $\frac{7}{12}$.
2. Since there are no critical points of f on the given interval and by Extreme Value Theorem [If f is a continuous function on an interval [a,b], then f has both a maximum and minimum values on [a,b]. ], we only need to check the endpoints, f(0) = 12, f(1) = 6 ⇒ f(0) = 12 is a maximum value of f on the interval [0, 1] (Figure iv).

If a function f is continuous on a closed interval, then the Extreme Value Theorem guarantees that f has both a maximum and a minimum value on that interval. By Fermat’s theorem, every local extremum in the interior of the domain of a differentiable function is necessarily a critical point. In our particular case (no critical values), this means that their extreme values can be found by evaluating the function at the endpoints of the interval.

• In Figure 1-5, we see several different possibilities for critical points. In some cases, the functions have local extrema (maximum -1-, -2- or minimum -3-) at critical points, whereas in other cases (4, 5) the functions do not.

How to find Absolute Extrema given a function f on a close interval [a, b]

1. Verify the function is continuous on [a, b].
2. Calculate the derivate and determine all its critical values.
3. Evaluate the function at the previous critical values and the endpoints, namely “a” and “b”.
4. Obviously, the absolute maximum value and absolute minimum value of f corresponds to the largest and smallest y-values respectively found in the previous step.

Solved exercises

• Find any absolute extrema for f(x) = |x| on the interval [-1, 1] -Figure 1-.

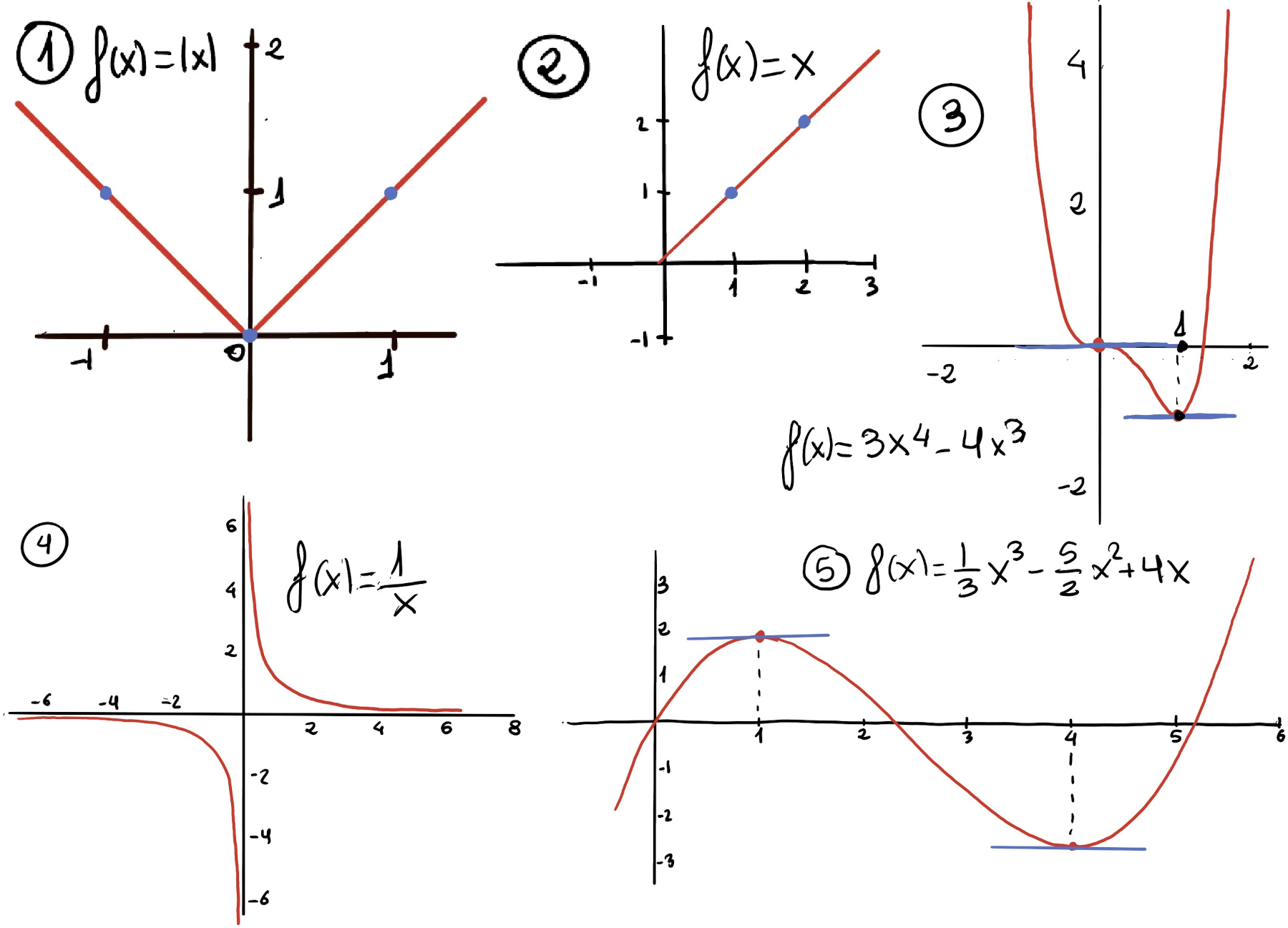
f is continuous, so by the Extreme Value Theorem f has an absolute maximum and an absolute minimum. Critical points: 0 (f’(0) is undefined). Endpoints: (1, 1) and (-1, 1) ⇒[To find any absolute extrema, we can simply evaluate the function at 0 -critical point-, 1, and -1 -endpoints-] The absolute maximums are at the points x = ± 1 and the absolute minimum is at x = 0 on the interval [-1, 1].

0 ∈ [-1, 1] is a local extremum, but f’(0) does not exist. This is an example of (3) in a previous diagram, 0 ∈ [-1, 1] is a local extremum, but f'(0) does not exist.

• Find any absolute extrema for f(x) = x on the interval [1, 2] -Figure 2-.

f is continuous and differentiable, so by the Extreme Value Theorem f has an absolute maximum and an absolute minimum, but f’(x) = 1 ≠ 0 ⇒ no critical points ⇒ [To find any absolute extrema, we can simply evaluate the function at 1 and 2] f(1) = 1 is an absolute minimum and f(2) = 2 an absolute maximum on the interval [1, 2].

• Find any absolute extrema for f(x) = 3x⁴-4x³ on the interval [-1, 2] -Figure 3-.

f is continuous and differentiable, so by the Extreme Value Theorem f has an absolute maximum and an absolute minimum. f’(x) = 12x³ -12x² = 0 ↭ x(x -1) = 0 ↭ x = 0, 1 are critical points.

To find any absolute extrema, we can simply evaluate the function at its critical values (0 and 1) and the endpoints (-1 and 2), and we get (0, 0), (1, -1), (-1, 7) and (2, 16). Therefore, f has an absolute maximum at 2 (2, 16) and an absolute minimum at 1. This is an example of (4), f'(0) = 0, but f has not a local extrema on the interval [-1, 2] at x = 0.

• Find any absolute extrema for f(x) = $\frac{1}{x}$ on the interval [-1, 1] -Figure 4-.

f is not continuous at x = 0 ⇒ we cannot apply the Extreme Value Theorem. Futhermore, $\lim_{x \to 0⁺} \frac{1}{x} = ∞, \lim_{x \to 0⁻} \frac{1}{x} = -∞$ ⇒ f does not have any absolute extrema on [-1, 1].

• Find any absolute extrema for f(x) = $\frac{1}{3}x^3-\frac{5}{2}x^2 +4x$ on the interval [0, 5] -Figure 5-.

f is continuous and differentiable, so by the Extreme Value Theorem, f has an absolute maximum and an absolute minimum. f’(x) = $x^2-5x +4 = (x-4)(x-1)$ ⇒ the critical points are 1 and 4.

To find any absolute extrema, we can simply evaluate the function at its critical values (1 and 4) and the endpoints (0 and 5), and we get (1, $\frac{11}{6}$≈1.83), (4, $\frac{-8}{3}$≈-2.66), (0, 0), (5, $\frac{-5}{6}$≈-0.83). Therefore, f has an absolute maximum at 1 (1, $\frac{11}{6}$≈1.83), and an absolute minimum at (4, $\frac{-8}{3}$≈-2.66) on the interval [0, 5].

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.