The dihedral group

Do you still remember that I am still only fourteen?” I said, starting to lose my temper and grasping how Mum should feel like when Dad says things like, “Such a sophisticated perfume honey, how many litres and for how long did you need to soak in it? Come to my localhost, I will turn off my firewall, disable my antivirus, grant you sudo access, and show you my source code,” Apocalypse, Anawim, #justothepoint

Definitions

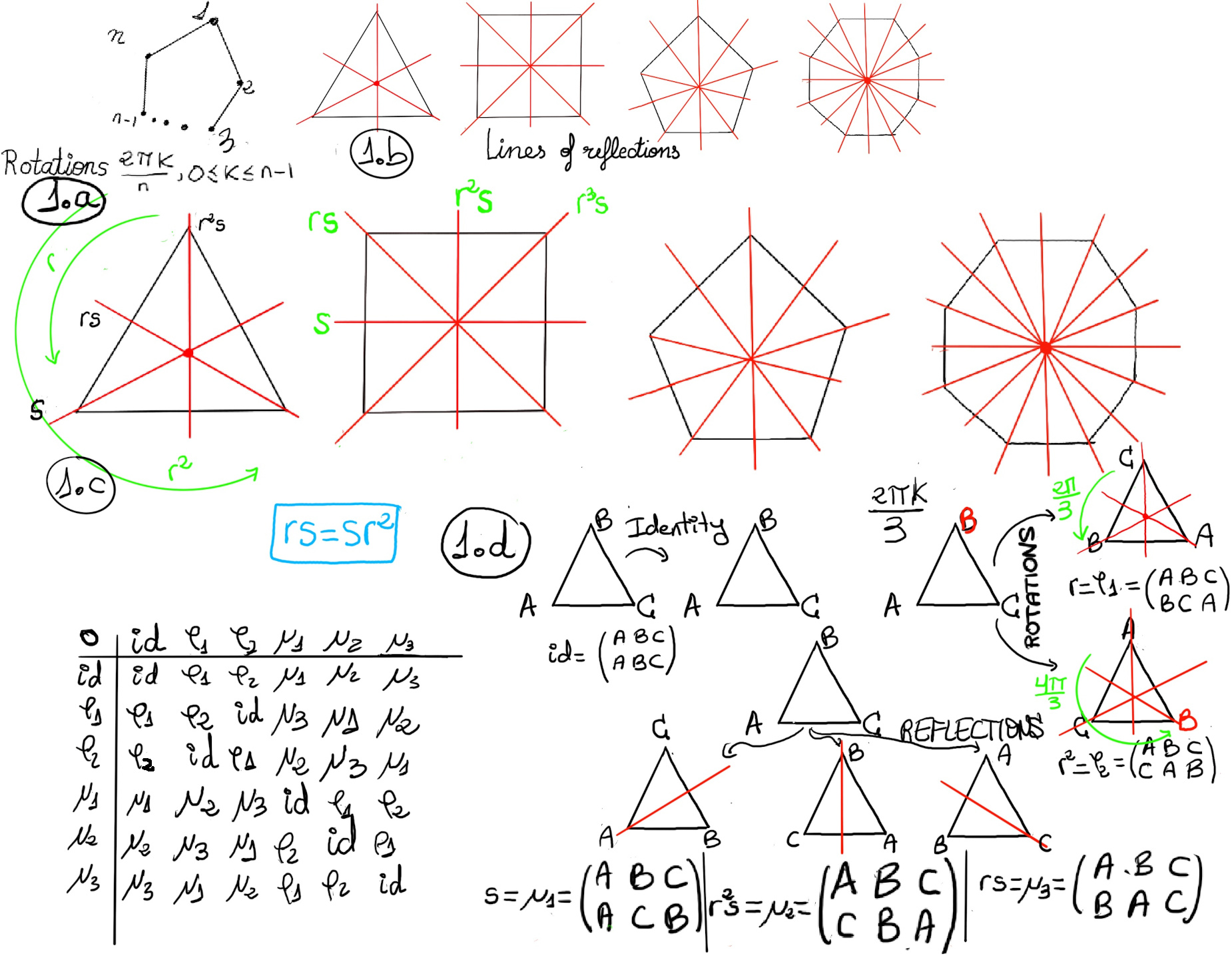
A polygon is a two-dimensional or plane figure that has a finite number of sides. It is described by a finite number of straight line segments connected to form a closed polygonal chain. A regular polygon is a polygon that is both equiangular (all angles are equal in measure) and equilateral (all sides have the same length).

The dihedral group D_n is the group of symmetries of a regular polygon with n vertices, which includes rotations and reflections or, in other words, the right motions taking a regular n-gon back to itself, or the arrangement of the figure preserving sides, vertices, distances, and angles.

A regular polygon can be rotated around its center in n different ways to come back to itself. More specifically, we can rotate it around the center by $\frac{2kπ}{n}$ radians where 0 ≤ k ≤ n − 1 (Figure 1.a).  

Any regular n-gon can be inscribed into a circle whose center coincides with the center of the n-gon. As the side lengths of the polygon are irrelevant in terms of symmetry, we could assume that our polygon is inscribed in the unit circle.

Let be r the counterclockwise rotation by θ = ^2π⁄_n, then the n rotations in D_n are e, r, r²,…, r^n-1, namely, 1, e^2π/n, e^2(2π/n), e^3(2π/n),···, e^(n-1)(2π/n), Figure 01.

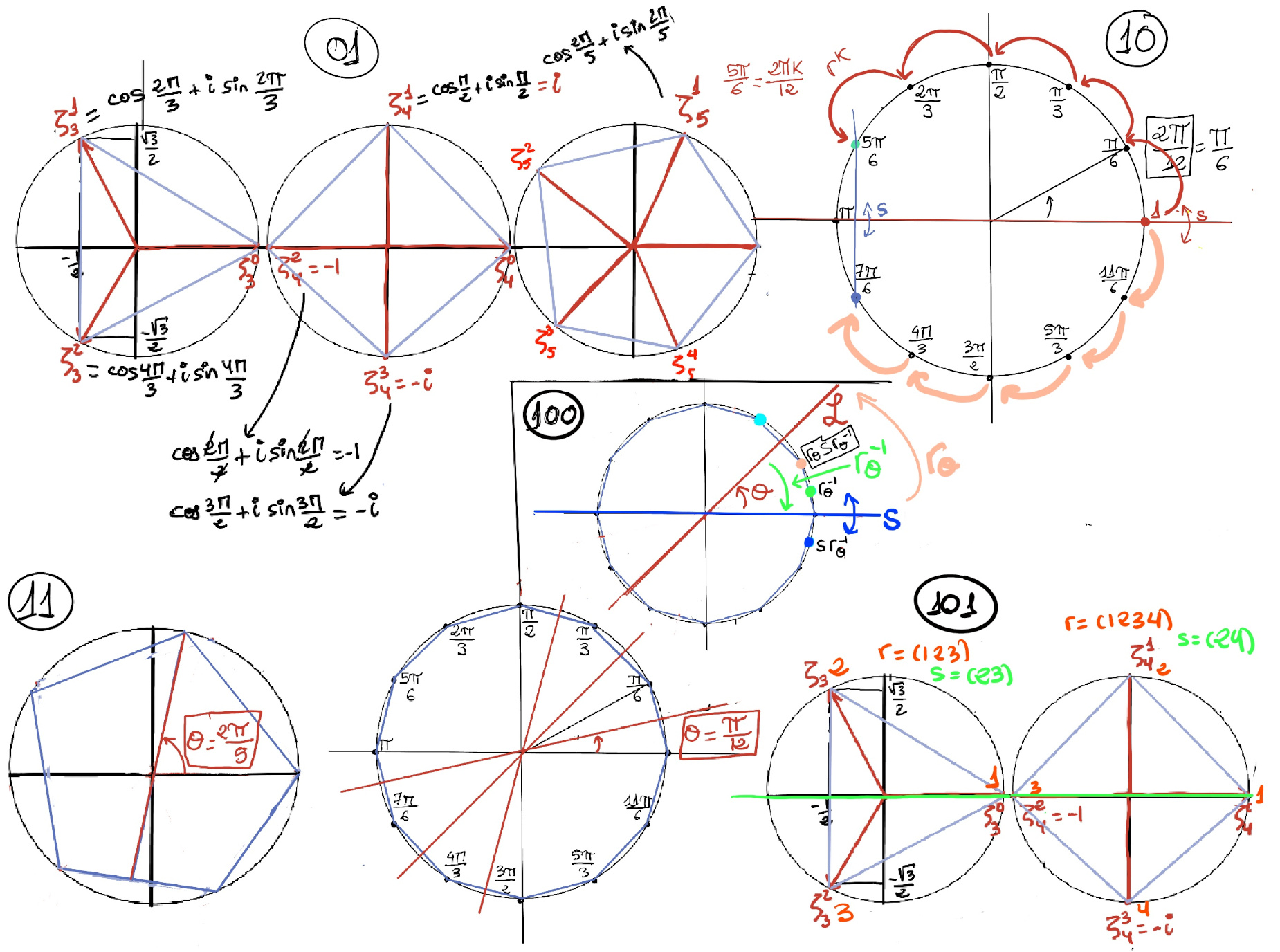
Theorem. Let s be a reflection across the real axis. Let D_n be the dihedral group. Then, sr^ks^-1 = r^-k. In particular, sr^k = r^-ks (by multiplying the previous equation by s).

Proof.

Consider sr^ks^-1 = [s² = 1 ⇒ s = s^-1] sr^ks = [sr^ks means to reflect across the x-axis, then rotate by θ = ^2πk⁄_n counterclockwise, that is, k rotations by r = ^2π⁄_n counterclockwise, and finally reflect across the x-axis back, but this is just a rotation by θ but clockwise, that is, k rotations by r^-1 clockwise, Figure 10. It is illustrated with P(1, 0)] (r^-1)^k = r^-k ∎

Theorem. D_n is generated by the symmetries r and s, D_n = ⟨r, s⟩. In particular, every symmetry σ can be expressed in the form σ = r^ks^l for k, l ∈ ℤ.

Proof.

We already know that the only symmetries of the unit circle are rotations and reflections. These are the only types of symmetries for the regular n-gon which is a subset of the unit circle.

1. Rotations. All counterclockwise rotational symmetries of the n-gon are power of r because they fix the center of the circle and every vertex of the n-gon needs to land on another vertex. Besides, all clockwise rotational symmetries of the n-gon are powers of r^-1.
2. Let ρ be a reflection across the line L. If ρ is a symmetry of the n-gon, then L must pass through both by the origin and a by vertex or a midpoint of an edge of the polygon. In either case, the angle θ that L makes with the positive real axis equals $k\frac{π}{n}$ for some k (Figure 11).
   It is not $k\frac{2π}{n}$ because L could pass thought the origin and a midpoint of an edge of the polygon.

Let r_θ be the rotation counterclockwise by θ. ρ = $r_θsr_θ^{-1}$ (Figure 100, r_θ^-1 is the rotation clockwise by θ) = [By the previous lemma, sr^ks^-1 = r^-k, sr^k = r^-ks, and sr^-k = s²r^ks^-1 = r^ks^-1 = r^ks, the angle θ that L makes with the positive real axis equals $k\frac{π}{n}$ for some k] r_θr_θs = r_2θs = [2θ = 2kπ/n, r is the rotation of 2π/n counterclockwise] r^ks ⇒ Every symmetry of our n-gon is generated by both r and s.

Each product of r’s and s’s is called a word, and we can simplify words by collapsing down adjacent r’s and s’s together, and we can consider that we don’t need inverses since s²=1 (s = s^-1) and sr^k = r^-ks. Therefore, a generic word in D_n has the following form, $σ=r^{k_0}sr^{k_1}sr^{k_2}···sr^{k_m}$ (k₀ and k_m could be zero, that is, a generic word can start and/or end with a rotation or a reflection).

Claim: σ = r^ks^l for k, l ∈ ℤ.

Let’s induct on the number of s’s in σ.

Case base. The number of s’s is 0 ⇒ σ = r^k₀ = r^k₀s⁰.

Suppose that if σ involves m-1 s’s, then σ = r^ks^l for some k, l ∈ ℤ.

$σ=r^{k_0}sr^{k_1}sr^{k_2}···sr^{k_m}=(r^{k_0}sr^{k_1}sr^{k_2}···sr^{k_{m-1}})sr^{k_m}$ = [By our induction hypothesis] $(r^ks^l)sr^{k_m}=r^ks^{l+1}r^{k_m}$ =

Notice: s···_{l+1 times}···sr···_{km times}···r = … [By the previous lema, sr^k=r^-ks each of the k_m r’s can be flipped by an s and needs to be moved l+1 times] = s···_{l times lefts to go}···(r^-1s)·r···_{km-1 times}···r = r^(-1)l+1s···_{l+1 times}···sr···_{km-1 times}···r

= $r^kr^{(-1)^{l+1}}··_{k_m}··r^{(-1)^{l+1}}s^{l+1} = r^kr^{(-1)^{l+1}k_m}s^{l+1}$ ∎

Lemma. Every symmetry σ can be expressed in the form σ = r^ks^l for k, l ∈ ℤ. It is called the normal form of σ and is unique up to modulo n on k and modulo 2 on l.

Proof.

Let’s suppose by reduction to the absurd that σ = r^ks^l = r^k’s^l’ ⇒ r^-k’r^k = s^l’s^-l, the product of rotations is itself a rotation, and the product of reflections is also a reflection, that’s impossible, therefore the only option left is the identity.

r^-k’r^k = s^l’s^-l ⇒ r^-k’r^k = s^l’s^-l = id ⇒ r^k = r^k’ and s^l’ = s^l ⇒ k ≡ k’ (mod n) and l ≡ l’ (mod 2) since s² = rⁿ = e∎

Theorem. The size of D_n is 2n.

Proof.

We have already demonstrated in the previous lemma that ∀σ ∈ D_n, σ = r^ks^l and this expression is unique up to modulo n on k and module 2 on l since s² = rⁿ = e, so the options are 0 ≤ k ≤ n-1 and 0 ≤ l ≤ 2 ⇒ |D_n| = 2n ∎

Theorem. Let s be reflection across a line through a vertex. The n reflections in D_n are s, rs, r²s,..., r^n-1s. Figure 1.b and 1.c.

Proof. The rigid motions s, rs, r²s,…, r^n-1s are different since e, r, r²,…, r^n-1 are different. Futhermore, s is not a rotation. Then, we claim that r^ks is not a rotation either.

Suppose for the sake of contradiction, r^ks is a rotation ⇒ r^ks = r^l ⇒ s = r^l-k, but s is not a rotation, but a reflection ⊥ (contradiction).

Therefore, D_n = {e, r, r²,…, r^n-1, s, rs, r²s,…, r^n-1s}

A reflection has order 2, so s² = 1 and s^-1 = s. The elements of D_n are rotations or reflections and the product of a rotation and a reflection is always a reflection. The geometric interpretation of s, rs, r²s,…, r^n-1s is as follows: starting from a vertex fixed by s, we draw all lines of reflections for a regular n-gon by moving clockwise $\frac{2kπ}{n}$ radians where 0 ≤ k ≤ n − 1.

The rigid motions r and s do not commute, but sr^n-1 = rs, and therefore D_n = {e, r, r²,…, r^n-1, s, rs, r²s,…, r^n-1s} = ⟨r, s | rⁿ = s² = e, rs = sr^n-1⟩.

A reflection is a transformation that acts like a mirror. A line that reflects a figure onto itself is called a line of symmetry.

Exercise. Let n = 6. Compute rsr⁴sr³ = [∴ Associativity] (rs)r⁴sr³ = [∴ n=6, rs=sr^n-1=sr⁵] sr⁵r⁴sr³ = sr⁹sr³ = [∴ r⁹ = r³, 9 ≡₆ 3] sr³sr³ = (sr³)² = [A rotation compose with a reflection is always a reflection and a reflection compose with itself is the identity] e.

Theorem. r^ks = sr^n-k, 1 ≤ k ≤ n-1.

Proof. Induction. Base case (k = 1) is already based on the definition of the dihedral group, D_n = ⟨r, s | rⁿ = s² = e, rs = sr^n-1⟩.

Let’s assume that the hypothesis holds for k.

r^k+1s = r (r^ks) = [k induction hypothesis] r(sr^n-k) = [Associativity] (rs)r^n-k = sr^n-1r^n-k = sr^n+n-(k+1) = [rⁿ = e] sr^n-(k+1) ∎

The dihedral group D₃

D₃ is the symmetry group of the equilateral triangle. An equilateral triangle is a triangle in which all three sides are the same length, that is, a regular polygon with three equal sides with angles of the same measure (60°).

D₃ = {id (e), rotations (ρ₁ -120° around the center anticlockwise-, ρ₂ -240°-), reflections or mirror images on all its vertices (μ₁, μ₂, and μ₃)} = {e, r, r², s, rs, r²s} = ⟨r, s | r³ = s² = e, rs = sr²⟩.

• 1 = e = ().
• 120° around the center anticlockwise, r = ρ₁ = $(\begin{smallmatrix}A & B & C\\ B & C & A\end{smallmatrix}) = (\begin{smallmatrix}1 & 2 & 3\\ 2 & 3 & 1\end{smallmatrix}) = $ (123).
• r² = ρ₂ = $(\begin{smallmatrix}A & B & C\\ C & A & B\end{smallmatrix}) = (\begin{smallmatrix}1 & 2 & 3\\ 3 & 1 & 2\end{smallmatrix}) = $(132).
• s = μ₁ = $(\begin{smallmatrix}A & B & C\\ A & C & B\end{smallmatrix}) = (\begin{smallmatrix}1 & 2 & 3\\ 1 & 3 & 2\end{smallmatrix})$ = (23).
• rs = μ₃ = $(\begin{smallmatrix}A & B & C\\ B & A & C\end{smallmatrix}) = (\begin{smallmatrix}1 & 2 & 3\\ 2 & 1 & 3\end{smallmatrix})$ = (12).
• r²s = μ₂ = $(\begin{smallmatrix}A & B & C\\ C & B & A\end{smallmatrix}) = (\begin{smallmatrix}1 & 2 & 3\\ 3 & 2 & 1\end{smallmatrix})$ = (13). Figure 101.

D₃ is not Abelian, e.g., ρ₁μ₁ = (123)(23) = (12) = μ₃ ≠ μ₁ρ₁ = (23)(123) = (13) = μ₂

The dihedral group D4

A square is a regular quadrilateral (four-sided polygon), which means that it has four equal sides and four equal right angles (90° angles, π/2 radian angles). The dihedral group D4 is the symmetry group of the square.

D4 = {id (e), rotations (ρ₁ -90° around the center anticlockwise-, ρ₂ -180°-, and ρ₃ -270°-), reflections or mirror images in the x -horizontal- and y -diagonal- axes (μ₁, μ₂), and reflections in the diagonals δ₁ and δ₂ respectively} = {e, r, r², r³, s, rs, r²s, r³s} = ⟨r, s | r⁴ = s² = e, rs = sr³⟩.

• 1 = e = R₀ = ().
• r = ρ₁ = R₉₀ -90° around the center anticlockwise- = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 2 & 3 & 4 & 1\end{smallmatrix})$ = (1234).
• r² = ρ₂ = R₁₈₀ -180° around the center anticlockwise- = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 3 & 4 & 1 & 2\end{smallmatrix})$ = (13)(24).
• r³ = ρ₃ = R₂₇₀ -270° around the center anticlockwise- = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 4 & 1 & 2 & 3\end{smallmatrix})$ = (1432).
• s = μ₁ = H = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 2 & 1 & 4 & 3\end{smallmatrix})$ = (12)(34).
• rs = δ₁ = D = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 3 & 2 & 1 & 4\end{smallmatrix})$ = (1234)(12)(34) = (13).
• r²s = μ₂ = V = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 4 & 3 & 2 & 1\end{smallmatrix})$ = (13)(24)(12)(34) = (14)(23).
• r³s = δ₂ = D’ = $(\begin{smallmatrix}1 & 2 & 3 & 4\\ 1 & 4 & 3 & 2\end{smallmatrix})$ = (1432)(12)(34) = (24)

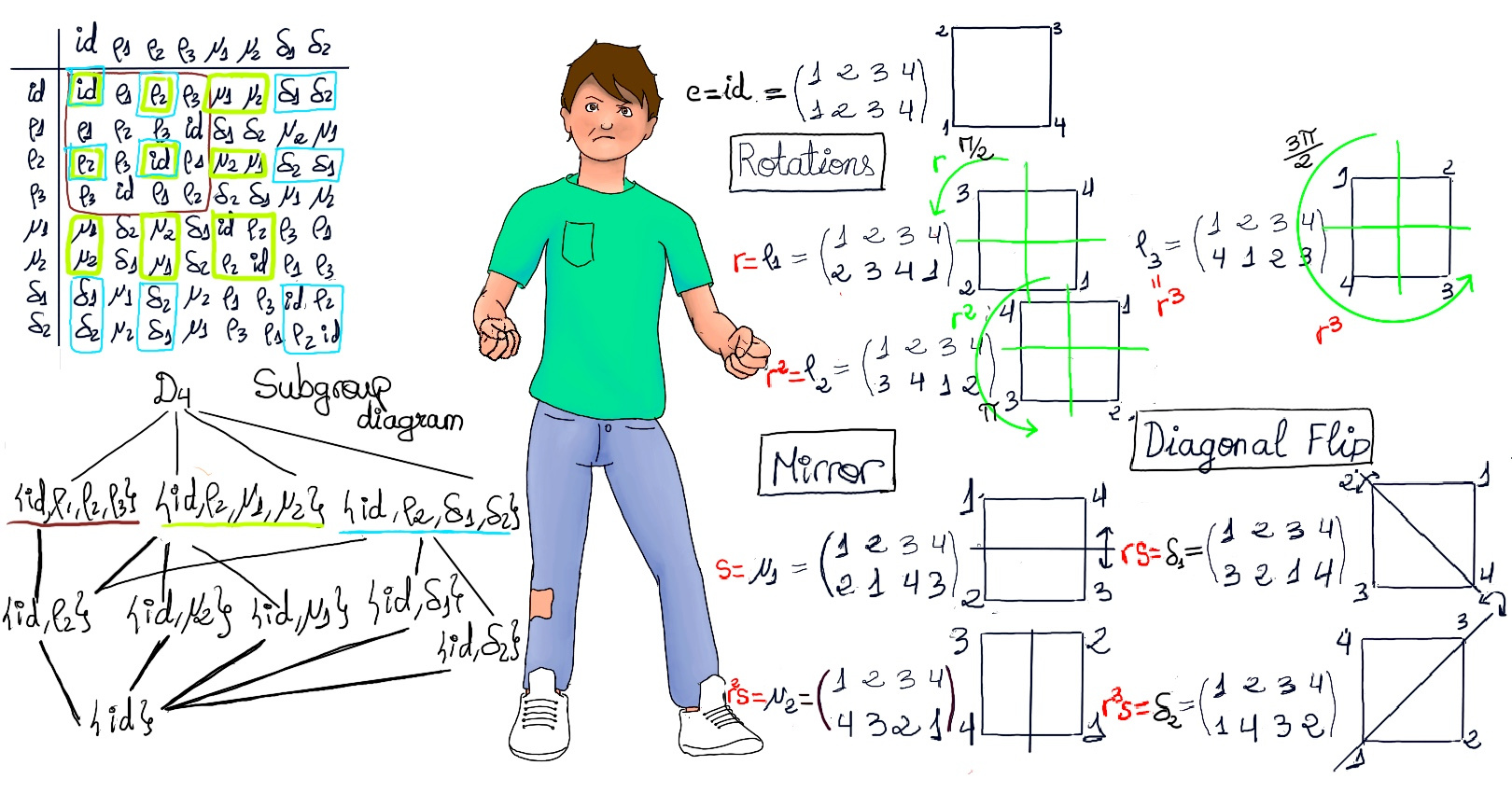
D4 is not Abelian, e.g. μ₁ρ₁ = (12)(34)(1234) = (24) = δ₂ ≠ ρ₁μ₁ = (1234)(12)(34) = (13) = δ₁.

Cosets

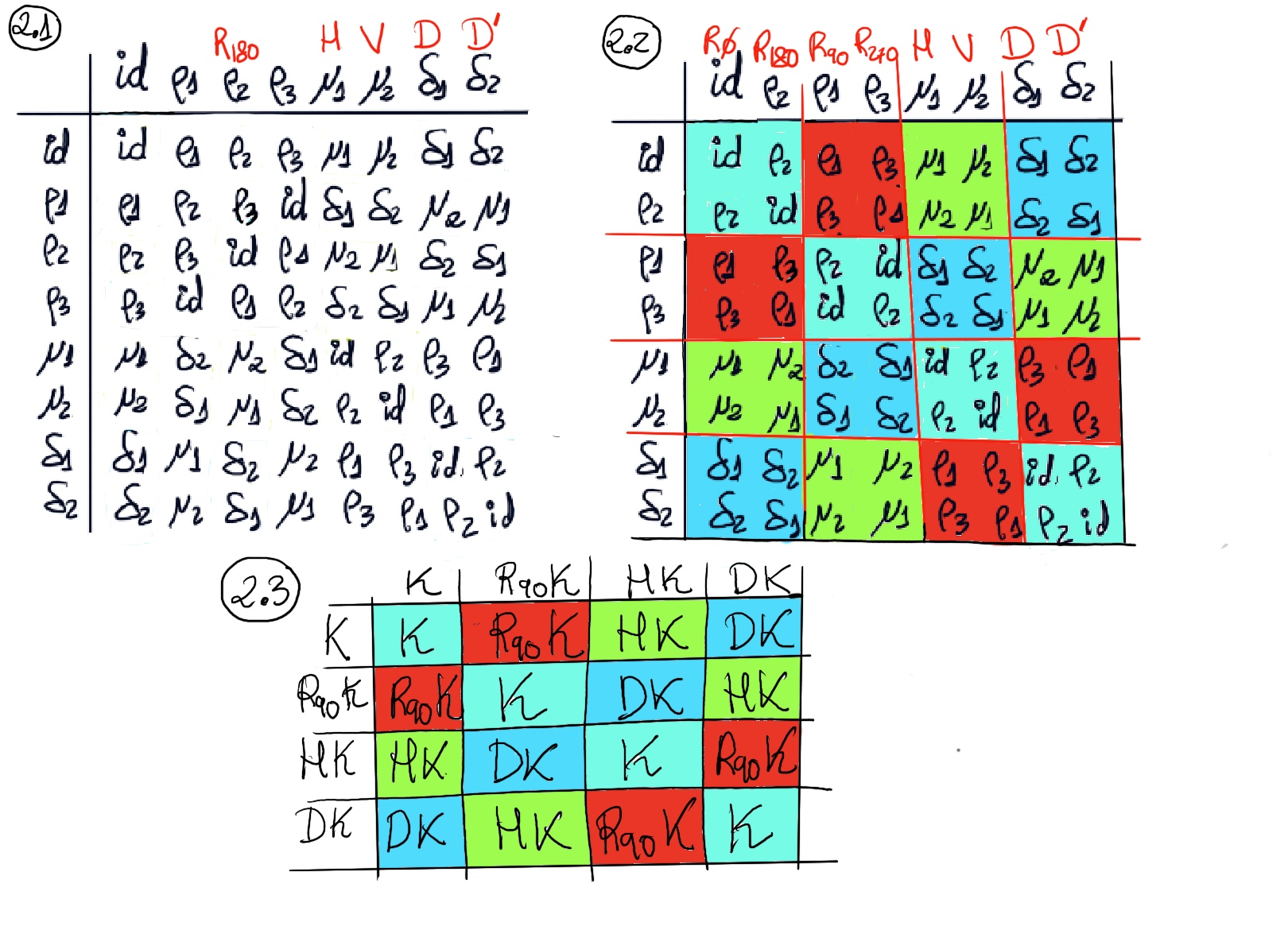
$K$ = {R₀, R₁₈₀} = ⟨R₁₈₀⟩. Let $K$ be the subgroup of D₄ generated by R₁₈₀, this subgroup is normal, $K$ ◁ D₄.

$D_4/K$ = {$K, R_{90}K, HK, DK$} where $K$ = {R₀, R₁₈₀}, $R_{90}K$ = {R₉₀, R₂₇₀}, $HK$ = {HR₀, HR₁₈₀} = {H, V}, $DK$ = {DR₀, DR₁₈₀} = {D, D’}.

Its multiplication table is given in Table 2.3. Observe that the multiplication table for D₄ can be simplified into small boxes that are cosets of $K$. We can represent an entire box by a single element of the box!

Center

Definition. The center of a group, G, is the set of elements that commute with all the elements of G. Z(G) = {g ∈ G | gx = xg, ∀x ∈ G}.

Center of D_n ℤ(D_n) = $ \begin{cases} e, n~is~ odd\\\\ e~ and~ α^{\frac{n}{2}}, n~is~ even \end{cases}$

Abstract

The dihedral group D_n is the group of symmetries of a regular polygon with n vertices, which includes rotations and reflections or, alternatively, the rigid motions taking a regular n-gon back to itself. D_n = {e, r, r²,…, r^n-1, s, rs, r²s,…, r^n-1s} = ⟨r, s | rⁿ = s² = e, rs = sr^n-1⟩.

1. 1, r, r²,…, r^n-1 are all distinct, rⁿ = 1, |r| = n.
2. |s| = 2.
3. s ≠ rⁱ ∀i, srⁱ ≠ sr^j, ∀i, j: 0 ≤ i, j ≤ n-1, i ≠ j.
4. rs = sr^-1
5. rⁱs = sr^-i ∀i, j: 0 ≤ i ≤ n

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.