Differential equations

The real problem of humanity is the following: We have Paleolithic emotions, medieval institutions and godlike technology. And it is terrifically dangerous, and it is now approaching a point of crisis overall, Edward O. Wilson.

Now I Am Become Death, the Destroyer of Worlds, Oppenheimer.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.  

Differential equations

Definition. Differential. An equation involving one dependent variable, one or more independent variable and the differential coefficient (derivatives) of dependent variable with respect to an independent variable is called differential equation, e.g., $\frac{dy}{dx} = 3x +5y, \frac{dy}{dx} = x^2y+y, etc.$

$\frac{dy}{dx}=f(x)$. This is the ratio between the change in y and the change in x ↭ the ratio of delta-y over delta-x as delta-x approaches 0. The solution is the antiderivate or the integral, y = $\int f(x)dx$

Another way of putting it would be, $\frac{dy}{dx}=f(x) ⇒ dy = f(x)dx ⇒ y = \int dy = \int f(x)dx$

Examples

• $\frac{dy}{dx} = x^2y+y$ ⇒[Let’s separate variables] $\frac{dy}{dx} = y(x^2+1) ⇒ \frac{1}{y}·\frac{dy}{dx} = x^2 + 1 ⇒ \int \frac{dy}{y} = \int (x^2 + 1)dx ⇒ ln|y| = \frac{x^3}{3}+x + c.$

• $\frac{dy}{dx} = x^3·y^2$ ⇒[Let’s separate variables] $\frac{1}{y^2}·\frac{dy}{dx} =x^3 ⇒ \int \frac{dy}{y^2} = \int x^3dx ⇒ \frac{-1}{y} = \frac{x^4}{4} + C.$

• $\frac{dy}{dx}+xy=0$.

$\frac{dy}{dx}=-xy$🚀 ⇒ $\frac{dy}{y}=-xdx$ ⇒ $\int \frac{dy}{y}=-\int xdx ⇒ ln|y| = \frac{-x^2}{2}+C ⇒ $ (where y ≠ 0)

In fact, $ln|y|+c_1 = \frac{-x^2}{2}+c_2 ⇒ ln|y| = \frac{-x^2}{2}+c$ where c = c₂ - c₁. In other words, two constants can always be combined.

$e^{ln|y|}= e^{\frac{-x^2}{2}+C} ⇒ |y| = ae^{\frac{-x^2}{2}} ⇒ y = ±ae^{\frac{-x^2}{2}}$ where a = e^c. Besides, the solution c works for any a because $\frac{dy}{dx}=a(-x)e^{\frac{-x^2}{2}}=-x|y|$🚀 Therefore, we have a general solution or a “family” of solutions. If we know a initial condition, say y(0) = 3 ⇒ 3 = y = $ae^{\frac{-x^2}{2}} = a$ ⇒ y = $3e^{\frac{-x^2}{2}}$ and the ambiguity of the general solution is indeed solved.

• $\frac{dy}{dx} = \frac{e^x}{y},$ y(0) = 1, y ≠ 0.

$\frac{dy}{dx} = \frac{e^x}{y}$ ⇒[Let’s separate variables] $y·\frac{dy}{dx} = e^x ⇒ \int y·dy = \int e^x dx ⇒ \frac{y^2}{2} = e^x + C$.

y(0) = 1, $\frac{1}{2} = e^0 + C = 1 + C ⇒ C = -\frac{1}{2} ⇒ \frac{y^2}{2} = e^x -\frac{1}{2}.$

Separation of Variables

$\frac{dy}{dx}=f(x)g(y) ⇒ \frac{dy}{g(y)}=f(x)dx ⇒ H(y) = \int \frac{dy}{g(y)};~ F(x) = \int f(x)dx $. Finally, we know that if these are both antiderivates of the same thing, then they have to differ by a constant, say H(y) = F(x) + C -implicit equation-, where C is a constant. Previously y is defined implicitly, you may want to do it an explicit equation, y = H^-1(F(x) + C).

Differential Equations: Integral Factors

Integrating factors are a useful method for solving linear ordinary differential equations (ODEs) of the form:

$\frac{dy}{dx} +P(x)y = Q(x)$ where P(x) and Q(x) are continuous functions of x. The integrating factor, μ(x), is defined as $μ(x) = e^{\int P(x)dx}$

The solution to the differential equation is obtained by multiplying both sides of the equation by the integrating factor $μ(\frac{dy}{dx} +P(x)y) = μ·Q(x)$, which becomes $\frac{d}{dx}(μ·y)=μ·Q(x)$ (💡Recognize the left side as the derivative of a product.) and then integrating both sides with respect to x, $μ·y = \int μ·Q(x)dx$, and now the ODE can be solved.

• $\frac{dy}{dx} -3y = 6$. First, we notice that it’s in the form $\frac{dy}{dx} +P(x)y = Q(x)$ where P(x) = -3 and Q(x) = 6.

Second, we find the integrating factor, μ(x). It is defined as $μ(x) = e^{\int P(x)dx} = e^{\int -3dx} = e^{-3x}$

Third, we write the differential equation in the form $\frac{d}{dx}(μ·y)=μ·Q(x)$ by multiplying both sides of the differential equation by the integrating factor, $e^{-3x}(\frac{dy}{dx} -3y) = 6·e^{-3x} ↭ \frac{d}{dx}(e^{-3x}·y) = 6·e^{-3x}$.

Fourth, we can solve the differential equation integrating with respect to x, $e^{-3x}·y = \int 6·e^{-3x}dx$ =[u = -3x, du = -3dx ⇒ $dx = \frac{-du}{3}$] $\int -2e^udu = -2e^u = -2e^{-3x} + C ⇒ e^{-3x}·y = -2e^{-3x} + C$ where C is the constant of integration.

Finally, solving for y, we get y = $-2 + C·e^{3x}$

• $\frac{dy}{dx} + 2y = x^2.$ First, we notice that it’s in the form $\frac{dy}{dx} +P(x)y = Q(x)$ where P(x) = 2 and Q(x) = x².

Second, we find the integrating factor, μ(x). It is defined as $μ(x) = e^{\int P(x)dx} = e^{\int 2dx} = e^{2x}$

Third, we write the differential equation in the form $\frac{d}{dx}(μ·y)=μ·Q(x)$ by multiplying both sides of the differential equation by the integrating factor, $e^{2x}(\frac{dy}{dx} + 2y) = e^{2x}·x^2 ↭ \frac{d}{dx}(e^{2x}·y) = e^{2x}·x^2$.

Fourth, we can solve the differential equation integrating with respect to x, $e^{2x}·y = \int e^{2x}·x^2 dx$ =[Recall Integration by parts formula $\int udv = uv - \int vdu$, u = x², dv = $e^{2x}dx$] $x^2\frac{1}{2}e^{2x}- \int \frac{1}{2}e^{2x}2xdx = \frac{1}{2}x^2e^{2x}- \int e^{2x}xdx$

$\int e^{2x}xdx$ =[Apply integration by parts again, u = x, dv = $e^{2x}dx, du = dx, v = \frac{1}{2}e^{2x}$] $\frac{1}{2}xe^{2x} -\int \frac{1}{2}e^{2x}dx = \frac{1}{2}xe^{2x} -\frac{1}{4}e^{2x} + C.$

Therefore, $e^{2x}·y = \frac{1}{2}x^2e^{2x}- \int e^{2x}xdx = \frac{1}{2}x^2e^{2x} -\frac{1}{2}xe^{2x} +\frac{1}{4}e^{2x} - C = e^{2x}(\frac{1}{2}x^2-\frac{1}{2}x+\frac{1}{4}) - C$ ⇒[Finally, we can solve for y] $y = \frac{1}{2}x^2-\frac{1}{2}x+\frac{1}{4} - C·e^{-2x}$

Solved exercises

• Let f(x) be a function such that the slope of the tangent to the curve at any point is twice the slope the ray from the origin.

$\frac{dy}{dx}=2\frac{y}{x}😄 ⇒ \frac{dy}{y} = \frac{2dx}{x} ⇒ \int \frac{dy}{y} = \int \frac{2dx}{x} ⇒ ln(y) = 2ln(x) + C ⇒ e^{ln(y)} = e^{2ln(x) + C} ⇒ y = ax^2~ where~ a=e^c$. If we want to be very strict, |y| = ax² ↭ y = ± ax² .

Futhermore, $\int \frac{dy}{y} = \int \frac{2dx}{x} ⇒ ln|y| = 2ln|x| + C$. Besides, y = ax² ⇒ $\frac{dy}{dx}=2ax=\frac{2ax^2}{x}=\frac{2y}{x}$😄 and it works for a > 0, a = 0, or a < 0. However, this is an unresolved problem when x = 0.

• Calculate the family of curves perpendicular or orthogonal to the family of parabolas y = ax². Differentiating y = ax² we get, $\frac{dy}{dx}=2ax$ =[Substituting a = $\frac{y}{x^2}$] = $2(\frac{y}{x^2})x = \frac{2y}{x}$

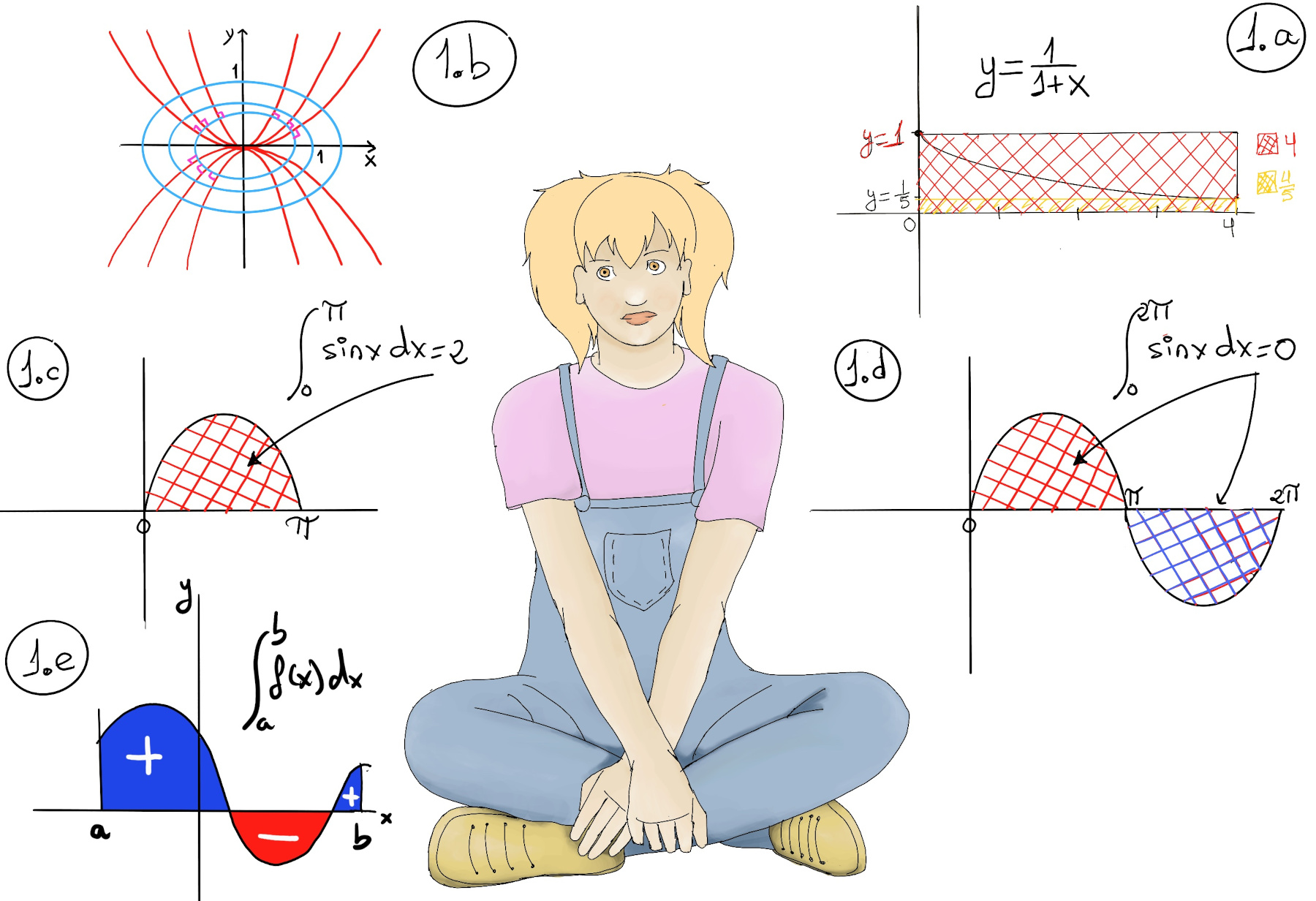
So the slope dy/dx at any point (x, y) of a curve orthogonal to the parabola passing through that point is $\frac{dy}{dx} = \frac{-1}{slope-of-tangent-to-parabola} = \frac{-1}{2y/x} =\frac{-x}{2y}$ ⇒[Separate variables] 2ydy = -xdx ⇒[Taking antiderivates] $\int 2ydy = \int -xdx ↭y^2 = \frac{-x^2}{2} + C ⇒ \frac{x^2}{2}+y^2 = C$ (Figure 1.b.).

Consider that the slope at any point (x, y) of an orthogonal curve is the negative reciprocal of the slope at the point (x, y) of the parabola passing through that point.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.