Higher derivatives

Listen to many advisors, but trust a few. Love all. Do wrong to none. Fear not, but trust god because He is faithful. Be courageous and strong, Anawim, #justtothepoint.

Recall

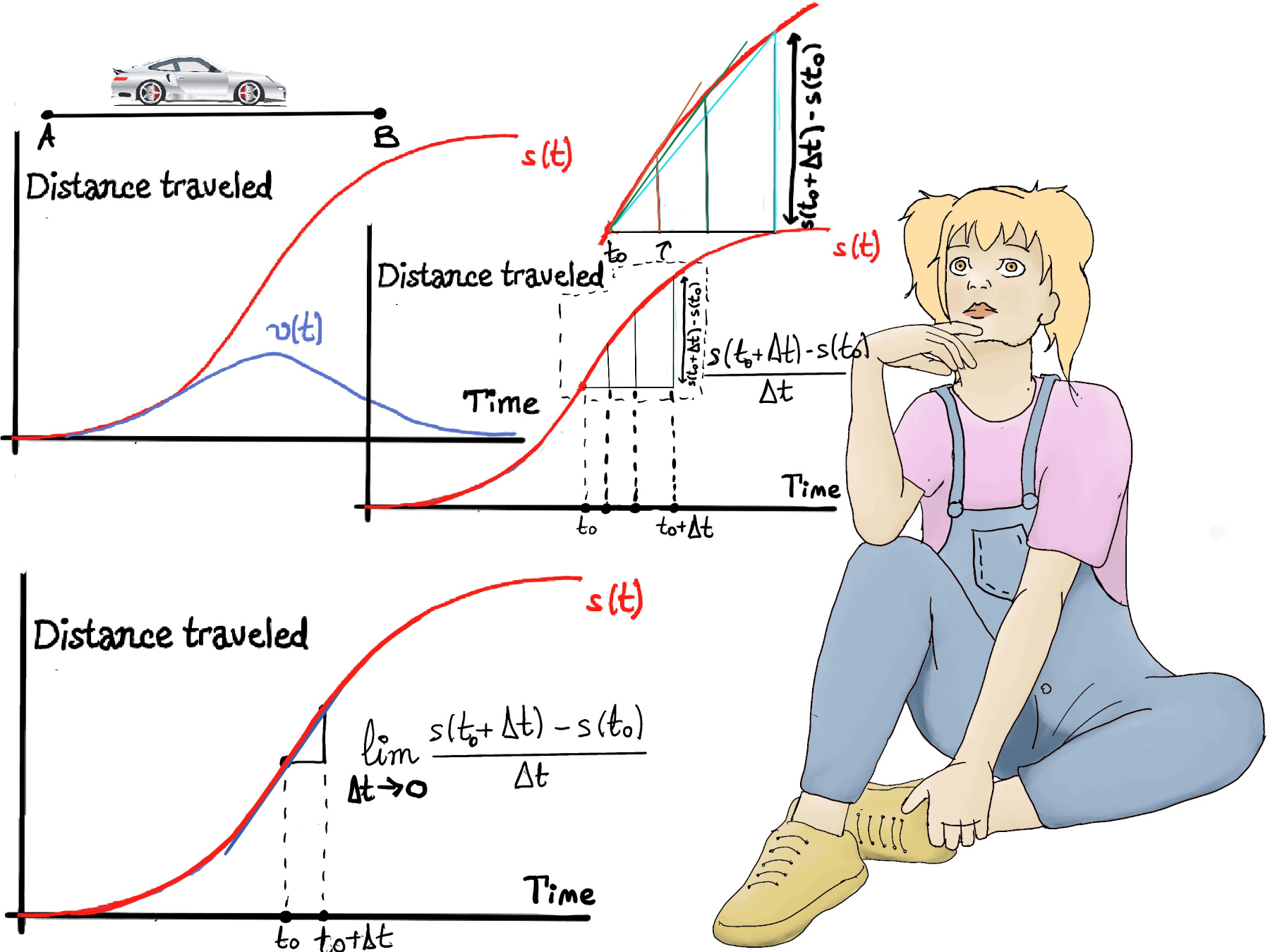
The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

Higher Order Derivatives.

Because the derivative of a function y = f(x) is itself a function, we can take its derivate, which is generally referred to as the second derivative of f and written as f"(x), f²(x), or even simply f". This differentiation process can be continued to find the third, fourth, and so on, which are called higher order derivatives of f.

Collectively the second, third, fourth, etc. derivatives are called higher order derivatives.

Other notations: f’= f’(x) = y’ = $\frac{dy}{dx}=\frac{d}{dx}y$. This is the differential operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.

y" = $\frac{d}{dx}\frac{dy}{dx}=\frac{d}{dx}\frac{d}{dx}y = (\frac{d}{dx})^{2}y = \frac{d^{2}y}{dx^{2}}.$

y³ = $\frac{d^{3}y}{dx^{3}} = D^{3}y$ and so on.

Interpretation

The first derivative of a function f(x), denoted as f'(x), represents the rate of change of f(x) with respect to x. Geometrically, it is the slope of the tangent line to the graph of f(x) at each point x. For example, if we are studying the motion of an object and we plot the distance traveled against time s(t), the slope of the graph represents the speed of the object, $\frac{ds}{dt}$. A steeper slope indicates a higher speed, while a flatter slope indicates a lower speed.

For example, if the rate of change of a company’s revenue is increasing, then it is likely that the company will continue to experience growth in the future.

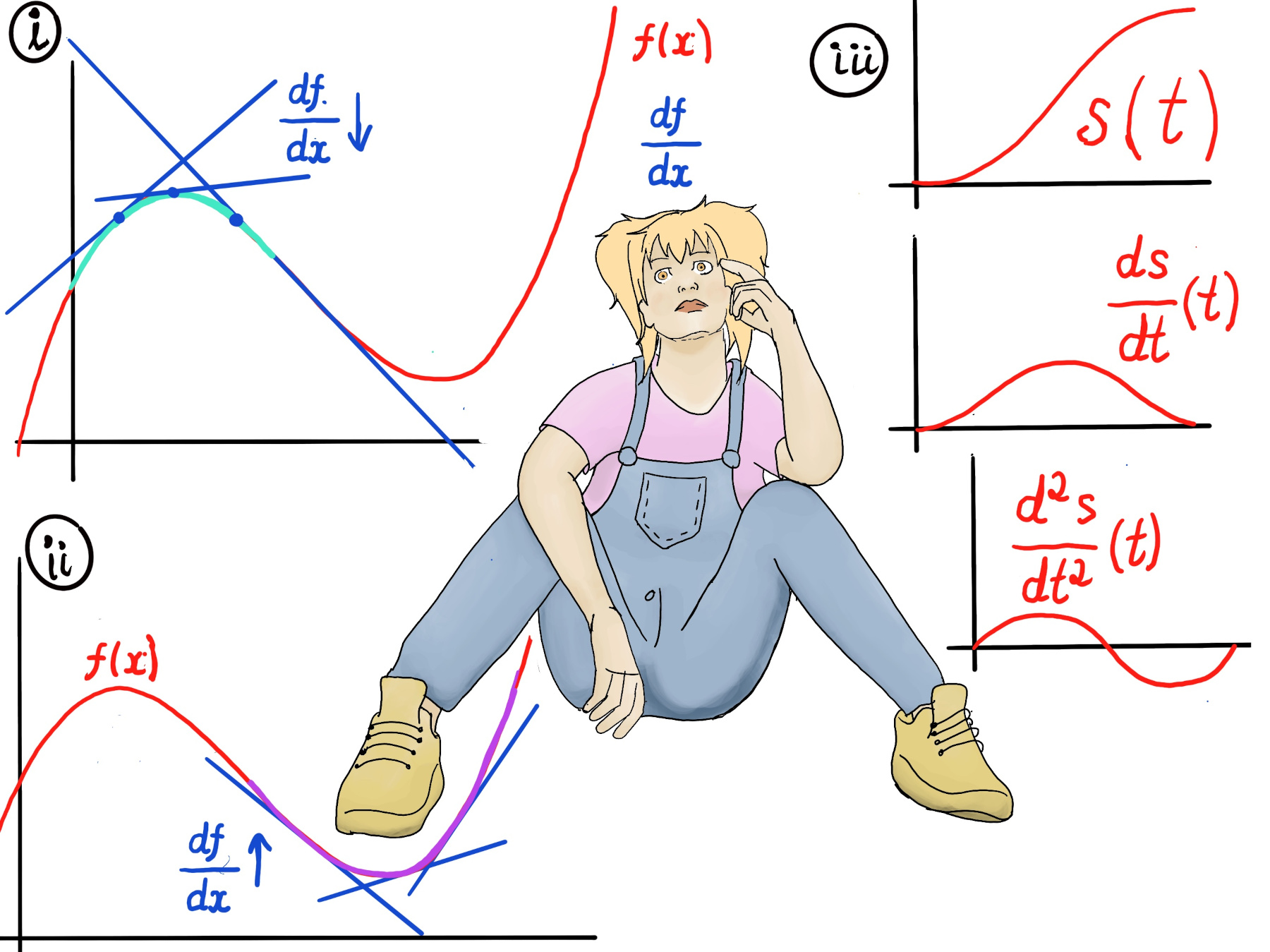
The second derivative, denoted as f’’(x) or $\frac{d^2f}{dx^2}$ represents the rate of change of the first derivative f’(x). It describes how the slope of the tangent line to the graph of f(x) is changing at each point x or, in other words, the curvature of the function.

At points where it curves upwards, the slope is increasing and that means the second derivative is positive. On the other hand, at points where it curves downwards, the slope is decreasing and that means the second derivative is negative.

Back to our previous example, if we are studying the motion of an object and we plot the distance traveled against time s(t), the second derivate is the object’s acceleration $\frac{d^2s}{dt^2}$, how the velocity changes as time passes. Therefore, we have positive acceleration whenever the car is speeding up (increasing velocity) and negative acceleration whenever the car is slowing down (decreasing velocity).

Let’s imagine a car 🚗 that starts at some city A (Madrid), speeds up, and then slows down to a stop at some city B (Barcelona). We could graph this motion (s(t)), letting the vertical axis (y) represents the distance traveled by the vehicle (measured in units such as meters, kilometers, miles, etc.), and the horizontal axis (x) represents the time taken to travel the distance (measured in units such as seconds, minutes, hours, etc.).

Initially the curve is quite shallow (commercial cars are typically slow to start), then for the next seconds, as the car speeds up, the distance traveled in a given time get larger or, in other words, the curve become steeper, and finally, as the car slows towards the end, the curve shallows out again, so the graph $\frac{ds}{dt}$ might look like a bump, increasing up to some maximum, then decreasing back to zero (Figure iii).

The acceleration’s curve is positive for the first half of the journey which indicates our vehicle is speeding up, then negative which indicates the car is slowing down.

Solved exercises

• $y = x^{m}.$ Let m = 1, $y’ = mx^{m-1}.~ y^{(’’)} = m(m-1)x^{m-2}.~ y^{(’’’)} =m(m-1)(m-2)x^{m-3}.~ y^{(n)}=m·(m-1)···(m-n+1)x^{m-n}.$

Induction. The formula is valid for n = 1. Assuming that it is true for n, let’s differentiate again.

$y^{(n+1)}=m·(m-1)···(m-n+1)(m-n)x^{m-n-1} = m·(m-1)···(m-n+1)(m-n)x^{m-(n+1)}$, that is, the derivative of (n+1)-th order is expressed by the same formula as the n-th order derivative (n is just replaced by n +1 ).

• y = sin(x), y’ = cos(x), y" = -sin(x), y³ = -cos(x), y⁴ = sin(x). We observe that the derivatives of sin(x) repeat every four derivatives due to the nature of the sine function. In other words, $y^{(4n)}=\frac{d^{4n}}{dx^{4n}} (sin(x))= sin(x), y^{(4n+1)}=\frac{d^{4n+1}}{dx^{4n+1}} (sin(x)) = cos(x), y^{(4n+2)}=\frac{d^{4n+2}}{dx^{4n+2}} (sin(x))= -sin(x), y^{(4n+3)}=\frac{d^{4n+3}}{dx^{4n+3}} (sin(x))= -cos(x)$, e.g., n = 50 = 4·12 + 2, $y^{(4n+2)} = y^{(4·12+2)} = -sin(x),$ n = 51 = 4·12 + 3, $y^{(4n+3)} = y^{(4·12+3)} = -cos(x).$

• Find the 99th and 100th derivate of y = sin(3x), y’ = 3cos(3x), y" = -3²sin(x), y³ = -3³cos(3x), y⁴ = 3⁴sin(3x) [···] We observe that the pattern repeats every four derivatives due to the nature of the sine function. Applying a similar argument to that used in the previous example, y⁹⁹ = y^{4·24 +3} =[y³ = -3³cos(3x)] -3⁹⁹cos(3x), y¹⁰⁰ = y^5·24 =[y⁴ = 3⁴sin(3x)] = 3¹⁰⁰sin(3x).

• Find the 100th derivate of y = e^-2x.

y’ = -2e^-2x, y’’ = (-2)²e^-2x, y’’’ = (-2)³e^-2x […] y⁽¹⁰⁰⁾ = (-2)¹⁰⁰e^-2x = 2¹⁰⁰e^-2x.

• y = $\frac{7}{x^2}$

y’ = $7·(-2)x^{-3} = \frac{(-1)^1·7·2·1}{x^3} = \frac{-14}{x^3}, y’’=-14·(-3)x^{-4} = \frac{42}{x^4} = \frac{(-1)^2·7·3·2·1}{x^4}, y’’’ = 42·(-4)x^{-5} = \frac{-168}{x^{5}} = \frac{(-1)^3·7·4·3·2·1}{x^4}$, and so on. As you can see, the pattern continues with alternating signs and increasing powers of x in the denominator. The nth derivative can be generally expressed as: $f^{(n)}(x) = (-1)^n \frac{7·(n+1)!}{x^{n+2}}$

• y = $\frac{1}{x-1}$

It is really quite similar, but you know what they say, practice makes perfect😄.

y’ = $(-1)(x-1)^{-2}, y’’=2·(x-1)^{-3}, y’’’ = 2·(-3)(x-1)^{-4} = (-6)(x-1)^{-4}, y’’’’ = (-6)·(-4)(x-1)^{-4}=24·(x-1)^{-4}$, and so on, hence $f^{(n)}(x) = (-1)^n·n!(x-1)^{-(n+1)} = \frac{(-1)^n·n!}{(x-1)^{(n+1)}}$

• y = $xe^x$

y’ = $e^x+xe^x =(x+1)e^x, y’’ =e^x +(x+1)e^x = (x+2)e^x, y’’’ = e^x + (x+2)e^x = (x+3)e^x ⇒ y^{(n)} = (x+n)e^x.$

Taylor series

An application of higher-order derivatives is in the Taylor series expansions, which are used to approximate functions with polynomials. The Taylor series of a function at a point x=a is: $f(x) = f(a) + f’(a)(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + ··· + \frac{f^{(n)}(a)}{n!}(x-a)^n + ···$.

Taylor series are a way to represent a function as an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. For most common functions, the function and the sum of its Taylor series are (almost) equal near this point, e.g., e^x =[e’(x) = e(x), e’’(x) = e(x), and so on] $\sum_{n=0}^∞ \frac{f^{(n)}(0)}{n!}x^n = \sum_{n=0}^∞ \frac{1}{n!}x^n$; sin(x) =[sin’(x) = cos(x), sin’’(x) = -sin(x), sin’’’(x) = -cos(x), sin⁴(x) = sin(x) and the pattern repeat, at x = 0, we get sin(0) = 0, sin’(0) = 1, 0, -1, 0] $\sum_{n=0}^∞ \frac{f^{(n)}(0)}{n!}x^n = x - \frac{x^3}{3!} + \frac{x^5}{5!}-\frac{x^7}{7!}+··· = \sum_{n=0}^∞ \frac{(-1)^n·x^{2n+1}}{(2n+1)!}$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.