Cyclic Groups II. Fundamental Theorem.

An expert is a person who has made all the mistakes that can be made in a very narrow field, Neils Bohr.

Recall

Definition. Let G be a group. A cyclic group G is a group that can be generated by a single element a. More formally, G is cyclic if there exists at least an element a ∈ G: G = ⟨a⟩ = {aⁿ | n ∈ ℤ}. We call such an element a generator of G.

The order of a is the number of elements in ⟨a⟩, that is, the order of the cyclic subgroup that it generates. For a finite cyclic group G of order n we have ⟨a⟩ = {e, a, a²,…, a^n-1}, where e is the identity element, aⁱ = a^j whenever i ≡ j (mod n). In particular, aⁿ = a⁰ = e and a^-1 = a^n-1. In other words, the order of a is the smallest positive integer n such that aⁿ = e, and we write it as |a| = n. If no such positive integer exists, we say that a has infinite order, |a| = ∞.

Theorem: Every cyclic group is Abelian.

Proof: If g and h ∈⟨a⟩ ⇒ g = a^m, h = aⁿ for some m, n ∈ Z ⇒ gh = a^m+n = a^n+m = aⁿa^m = hg∎

Theorem. Every subgroup of a cyclic group is cyclic.

Proof. Let G be cyclic, there exists at least an element a ∈ G: ⟨a⟩ = G. Suppose that H is a subgroup of G, H ≤ G. There are two possibilities, namely:

1. If H is the trivial subgroup, H = {e} ⇒ H = ⟨e⟩, and H is obviously cyclic.

2. Otherwise, if H is not the trivial subgroup, H ≠ {e} ⇒ ∃g ∈ H: g ≠ e, g = aⁿ ⇒ [Well-ordering principle. Every non-empty set of positive integers contains a least element.] Let m be the smallest natural number such that h = a^m ∈ H

We claim that H = ⟨h⟩ = ⟨a^m⟩. Let h’ be an arbitrary element of H, h’ ∈ H ⇒ h’ = a^k.

By the division algorithm, ∃q, r: k = mq + r where 0 ≤ r < m ⇒ a^k = a^mq+r = a^mqa^r = (a^m)^qa^r = h^qa^r ⇒ a^r = a^kh^-q ∈ H [h’ = a^k and h^-q∈ H], but r < m, and h = a^m is the smallest element in H ⇒ r = 0 ⇒ k = mq, h’ = a^k = a^mq = h^q, and therefore, since h’ was an arbitrary element of H and it is generated by h = a^m ⇒ H = ⟨h⟩ = ⟨a^m⟩∎

Theorem. Let G be a finite cyclic group, G = ⟨g⟩. Then, G has exactly one subgroup of order d for each d | |G|, namely H = ⟨g^n/d⟩ ≤ G

Proof

Let |G| = n. By assumption d | n, let us consider h = g^n/d. It is obvious that h^d = (g^n/d)^d = gⁿ = [G = ⟨g⟩, |G| = n] e.

If a ∈ ℤ, 1 ≤ a < d ⇒ [a < d ⇒ an/d < dn/d(=n)] 1 ≤ an/d < n. Thus, h^a = g^na/d ≠ e because 1 ≤ an/d < n and no power less than n can get g to the identity. Then, d is the smaller power that can get h to the identity ⇒ [By definition] |h| = d ⇒ |⟨h⟩| = d. So there is at least one such subgroup.

Let’s prove uniqueness. Let k ∈ G: |k| = d. G is cyclic so ∃m: k = g^m. g^dm = (g^m)^d = k^d = e ⇒ [g^a =e ↭ |g| | a] n | dm ⇒ ∃l ∈ ℤ: nl = dm ⇒ (n/d)l = m ⇒ k = g^m = (g^n/d)^l = h^l ∈ ⟨h⟩ ⇒ k = h^l ∈⟨h⟩ ⇒ ⟨k⟩ ⊆ ⟨h⟩, but these are two finite sets with the same order, so they are the same set ∎

Corollary. The subgroups of ℤ are exactly nℤ and the subgroups of ℤ_n are exactly mℤ_n.

Proof.

(ℤ, +) is an infinite cyclic group. nℤ = {nk | k ∈ ℤ} are all cyclic subgroups of ℤ by definition, but we have demonstrated that being ℤ cyclic (ℤ = ⟨1⟩), then all its subgroups are necessarily cyclic ⇒ These are exactly all the subgroups of ℤ, and more importantly, there are no other subgroups left.

By similar reasoning, ℤ_n is a cyclic finite group, all their cyclic groups are mℤ_n = {mk | k ∈ ℤ_n} by definition, and as was reasoned before, their only subgroups are cyclic subgroups, so the subgroups of ℤ_n are exactly mℤ_n.

Theorem. Let G be a finite cyclic group generated by an element a, G = ⟨a⟩, |G| = n. Then a^k = e iff n divides k.

Proof.

⇒) Let’s suppose that a^k = e. By the division algorithm, k = nq +r, where 0 ≤ r < n ⇒ a^k = a^nq+r = a^nqa^r ⇒ [a^k = e, a^nq=a⁰=e because aⁿ = e or it could also be argued that nq≡0 (mod n)] e = a^r ⇒ r = 0 because r < n and n is the smallest integer m such that a^m = e ⇒ k = nq ⇒ n | k.

⇐) Conversely, let’s suppose n divides k ⇒ k = ns for some integer s ⇒ a^k = a^ns = (aⁿ)^s = e^s = e∎

Exercise: Suppose G is cyclic, a ∈ G, a is an element of order n, and a²⁴ = e. What are the possibilities of n?

a²⁴=e ⇒ k = 24 ⇒ n|24 ⇒ n needs to be 1, 2, 3, 4, 6, 8, 12 or 24.

Proposition. Let G be an arbitrary group, a ∈ G, and let m, n ∈ ℤ. If aⁿ = e and a^m = e, then a^{gcd(m, n)} = 1.

Proof.

By the Euclidean Algorithm, there exists r, s ∈ ℤ such that d = mr + ns, d = gcd(m, n) =_notation (m, n) ⇒ a^d = a^mr+ns = a^mra^ns = (a^m)^r(aⁿ)^s = [By assumption, a^m = e, aⁿ = e] e^re^s = e∎

Theorem. Let a be an arbitrary element of order n in a group G, and let k be a positive integer. Then, ⟨a^k⟩=⟨a^gcd(n,k)⟩ and |⟨a^k⟩| = $\frac{n}{gcd(n,k)}.$

Proof.

Let b = a^k and d = gcd(k, n). We need to know the smallest integer m such that e = b^m = a^km. By the previous theorem, [Theorem. Let G be a finite cyclic group generated by an element a, G = ⟨a⟩, |G| = n. Then a^k = e iff n divides k.] this is the smallest integer m such that n divides km or n/d divides m(k/d). d = gcd(k, n), and therefore n/d and k/d are coprimes, [n/d|m(k/d), (n/d,k/d)=1]the smallest m s.t. n/d | m is m = n/d ⇒ [Let G be a finite cyclic group, G = ⟨g⟩. Then, G has exactly one subgroup of order d for each d | |G|, namely H = ⟨g^n/d⟩ ≤ G] ⟨a^k⟩ = ⟨a^n/d⟩ = ⟨a^n/gcd(k,n)⟩.

Example. Suppose |a|=24 and k=10. ⟨a^k⟩= ⟨a¹⁰⟩= ⟨a^gcd(n,k)⟩ = ⟨a^{gcd(24, 10)}⟩ = ⟨a²⟩ = {a², a⁴, a⁶, … a²², a⁰} and |⟨a¹⁰⟩| = $\frac{24}{gcd(24,10)}=\frac{24}{2}=12.$

Corollaries:

1. In a finite cyclic group, the order of an element divides the order of the group. Example: U₁₄ = {1, 3, 5, 9, 11, 13}, |U₁₄| = 6, so the order of their elements are 1, 2, 3, and 6. |⟨1⟩|=1; |⟨3⟩| = 6 and ⟨3⟩ = {3, 9, (3³ = 27 % 14 = 13) 13, 11, 5, 1} = ⟨5⟩, |⟨5⟩| = 6, |⟨9⟩|=3 and ⟨9⟩ = {9, 11, 1}, |⟨11⟩|=3, ⟨11⟩ = {11, 9, 1}, |⟨13⟩| = 2, ⟨13⟩ = {13, 1}.
2. Let |a| = n. Then ⟨aⁱ⟩=⟨a^j⟩ iff $\frac{n}{gcd(n,i)}=\frac{n}{gcd(n,j)}$ ↭ gcd(n, i) = gcd(n, j) and |aⁱ| = |a^j| = $\frac{n}{gcd(n,i)}$. Since G = ⟨a⟩ is a cyclic group, it has exactly one subgroup of order d for each d| |⟨a⟩|. Example: Suppose |a| = 15. Compute the orders of a⁶ and a⁸. |a⁶|= $\frac{15}{gcd(15, 6)}=\frac{15}{3}=5$. |a⁸|= $\frac{15}{gcd(15, 8)}=\frac{15}{1}=15$. In U₁₄, |3²| = $\frac{|3|}{gcd(|3|, 2)}=\frac{6}{gcd(6,2)}=\frac{6}{2} = 3$. In U₁₄, |⟨9⟩|=3 and ⟨9⟩ = {9, 11, 1}.
3. Let |a|=n. Then ⟨a⟩=⟨a^j⟩ iff $\frac{n}{gcd(n, j)}=n$ ↭ gcd(n, j) = 1. In particular, the number of generators of ⟨a⟩ is φ(n) where φ is Euler’s φ-function. Example: ⟨5⟩ = U₁₄ = {1, 3, 5, 9, 11, 13}, |U₁₄| = 6. Which other element generates U₁₄? gcd(6, j) = 1 ⇒ j = 1 (⟨5¹⟩ = ⟨5⟩ = U₁₄) and j = 5 (⟨5⁵⟩= [5² = 25 ≡₁₄ 11, 5³ = 55 ≡₁₄ 13, 5⁴ = 65 ≡₁₄ 9, 5⁵ = 45 ≡₁₄ 3] ⟨3⟩ = U₁₄.
4. An integer k ∈ ℤ_n is a generator of ℤ_n iff gcd(n, k) = 1. Addition notation, G = ℤ_n = ⟨1⟩, |G| = n, k ∈ ℤ_n ⇒ k = 1 + 1 + ··ₖ·· + 1 = k·1, ⟨k⟩ = G ↭ gcd(n, k) = 1.

As a result, the generators of ℤ_n are the integers k such that |⟨a^k⟩| =[a = 1 in ℤ_n = ⟨1⟩, k = k·1] |⟨k⟩| n/d = n where d = gcd(k, n) = 1. In other words, the generators of ℤ_n are the integers k that are relatively prime to n.

Examples:

• 1 and 3 are generators of ℤ₄ (φ(4) = 2), 1 and 5 are generators of Z₆ (φ(6) = 2), and 1, 5, 7, and 11 are the generators of ℤ₁₂ (φ(12) = 4).
• In ℤ₁₂, |⟨2⟩|= 12/gcd(12, 2)= 6, ⟨2⟩ = {0, 2, 4, 6, 8, 10}; |⟨3⟩|= 12/gcd(12, 3)= 4, ⟨3⟩ = {0, 3, 6, 9}; |⟨4⟩|= 12/gcd(12, 4)= 3, ⟨4⟩ = {0, 4, 8}; |⟨6⟩|= 12/gcd(12, 6)= 2, ⟨6⟩ = {0, 6}; |⟨9⟩|= 12/gcd(12, 9)= 12/3 = 4, ⟨3⟩ = ⟨9⟩ = {0, 3, 6, 9}.

Theorem. Let G be a cyclic group with generator a. If the order of G is infinite, then G is isomorphic to (ℤ, +). Otherwise, G is isomorphic to (ℤ_n, +_n)

Proof.

If the order of G is infinite, ∀m ∈ ℤ, m ≠ 0, a^m ≠ e. We claim that ∀h, k ∈ ℤ, a^h ≠ a^k. Suppose a^h = a^k and h > k ⇒ a^ha^-k = a^h-k = e ⊥ .i.e, contrary to our assumption that G is infinite. Therefore, ∀g ∈ G, g = a^m for a unique power m ∈ ℤ.

The map Φ: (G,·) → (ℤ, +), Φ(g) = Φ(a^m) = m is well defined (We have already demonstrated that ∀g ∈ G, g = a^m for a unique power m ∈ ℤ), homomorphism (∀g₁, g₂ ∈ G, ∃!m₁, m₂ s.t. g₁ = a^m₁, g₂ = a^m₂ ⇒ Φ(g₁·g₂) = Φ(a^m₁·a^m₂) = Φ(a^m₁+m₂) = m₁ + m₂ = Φ(g₁)+Φ(g₂)), one to one (m₁ = m₂ ⇒ g₁ = a^m₁ = a^m₂ = g₂), and onto ℤ (∀m ∈ ℤ, m ≠ 0, a^m≠e, a → m, e → 0) ⇒ G ≋ ℤ.

Let’s suppose the order of G is finite. a^m= e for some m ∈ ℤ, m > 0. Let n be the smallest positive integer such that aⁿ = e. The map Φ: G → ℤⁿ, given by Φ(aⁱ)=i, for i=0, 1, 2,…n-1 is well-defined, homomorphism, one to one, and onto ℤ_n ⇒ G ≋ ℤ_n

We claim that a⁰ (e), a, a², a³,… a^n-1 are all distinct and comprise all elements of G = ⟨a⟩, |G| = n.

Hint: s = nq + r, 0 ≤ r < n, a^s = a^nqa^r = (aⁿ)^qa^r =e^qa^r = a^r, a^r-s = e. If 0 < s < r < n, a^r-s = e and 0 < r-s < n so it contradicts our choice of n, r = 0 and s = nq. Besides, a⁰ (e), a, a², a³,… a^n-1 are all distinct.

is Φ homomorphism? Φ(g·g’) = Φ(g)+_nΦ(g’)? ∀g, g’ ∈ H, ∃i, j such that g = aⁱ, g’ = a^j

Let k = i +_n j, aⁿ = a⁰ = e ⇒ [a^k-(i+j) = a^l·n = e] a^k = a^i+j ⇒ aⁱa^j = a^k ⇒ Φ(aⁱa^j) = k = i +_n j = Φ(aⁱ) + Φ(a^j).

Corollary. Any two cyclic groups of the same order are isomorphic.

Proof

Let ⟨a⟩ and ⟨b⟩ be cyclic groups of order n, then the map Φ: ⟨a⟩ → ⟨b⟩ defined by, Φ(a^k) = b^k is well-defined and is an isomorphism (you may want to check this).

Is it well-defined? If a^r = a^s ⇒ Φ(a^r) = Φ(a^s) ↭ b^r = b^s

a^r = a^s ⇒ a^r-s = e ⇒ n | (r -s), say r -s = tn ⇒ r = tn +s ⇒ Φ(a^r) = Φ(a^tn+s) = b^tn+s = b^tnb^s = (bⁿ)^tb^s = b^s.

Classification of subgroups of cyclic groups

Fundamental Theorem of Cyclic Groups. Every subgroup of a cyclic group is cyclic. If ⟨a⟩=n, then the order of any subgroup of ⟨a⟩ is a divisor of n. For each positive divisor k of n, the group ⟨a⟩ has exactly one subgroup of order k, namely, ⟨a^n/k⟩

Example. Suppose G = ⟨a⟩ and |G|=20. List the subgroups G and their orders.

Orders of subgroups of G: 1, 2, 4, 5, 10, and 20.

• Order 1: ⟨a^n/k⟩ = ⟨a^20/1⟩ = ⟨a²⁰⟩ = {e}.
• Order 2: ⟨a^n/k⟩ = ⟨a^20/2⟩ = ⟨a¹⁰⟩ = {a¹⁰, e}.
• Order 4: ⟨a^n/k⟩ = ⟨a^20/4⟩ = ⟨a⁵⟩ = {a⁵, a¹⁰, a¹⁵, e}.
• Order 5: ⟨a^n/k⟩ = ⟨a^20/5⟩ = ⟨a⁴⟩ = {a⁴, a⁸, a¹², a¹⁶, e}.
• Order 10: ⟨a^n/k⟩ = ⟨a^20/10⟩ = ⟨a²⟩ = {a², a⁴, a⁶, a⁸,… e}.
• Order 20: ⟨a^n/k⟩ = ⟨a^20/20⟩ = ⟨a⟩ = G.

Corollary. For each positive divisor k of n, the set ⟨n/k⟩ is the unique subgroup of ℤ_n of order k.

Let φ(1) = 1 and for any n ∈ ℤ, n > 1, let φ(n) denote the number of positive integers less than n and relative prime to n, φ is the Euler phi function. If d is a positive divisor of n, the number of elements of order d in a cyclic group of order n is φ(d).

Proof.

By a previous result, Let G be a finite cyclic group, G = ⟨g⟩. Then, G has exactly one subgroup of order d for each d | |G|, namely H = ⟨g^n/d⟩ ≤ G. Hence, for each d | |G|, G = ⟨g⟩ has exactly one subgroup of order d, say ⟨a⟩, and we have also demonstrated that a^k generates ⟨a⟩ ↭ gcd(k, d) = 1 and this is by definition precisely φ(d)∎

Examples

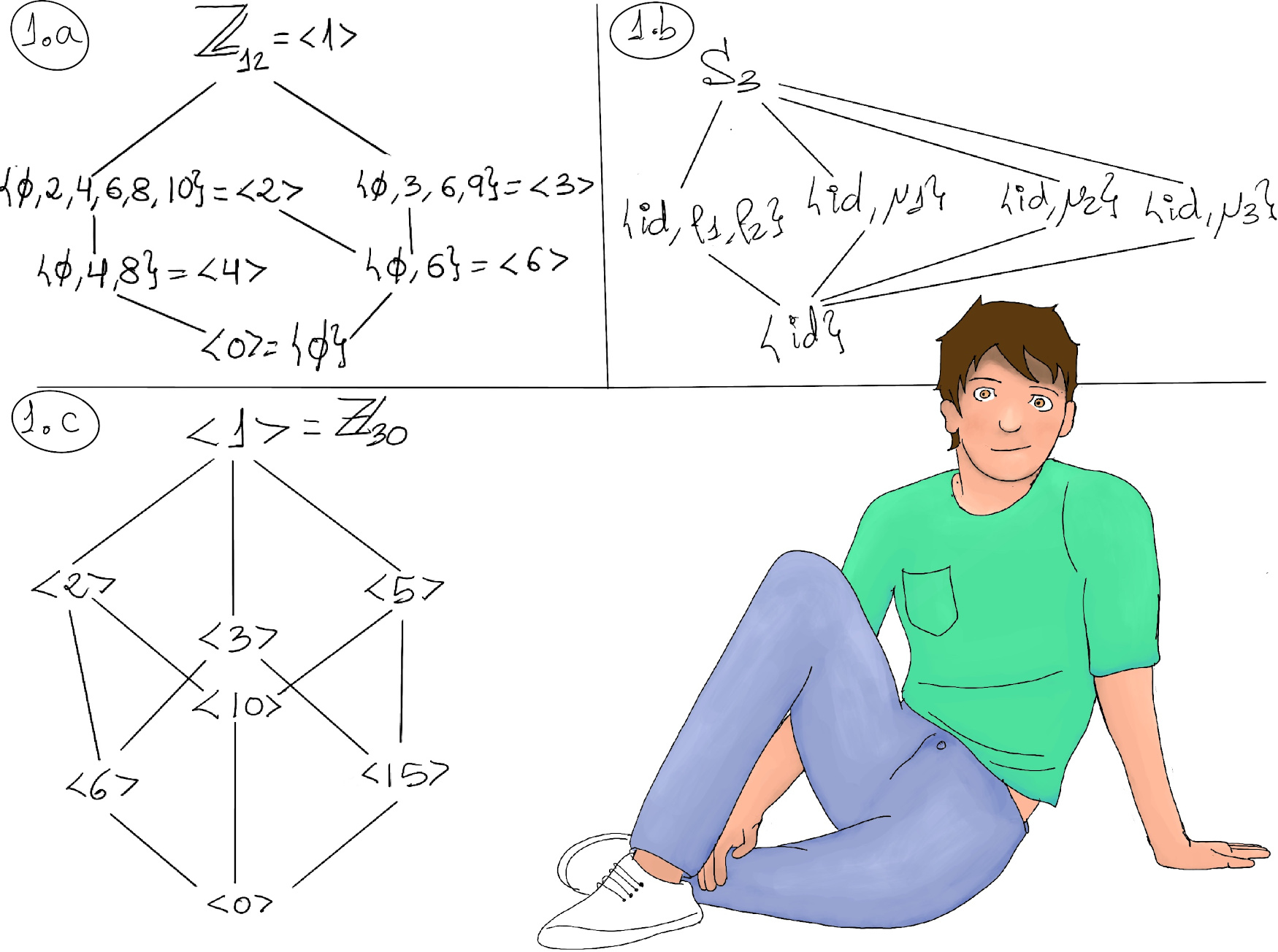
• ℤ₁₂. Order of subgroups are: 1, 2, 3, 4, 6, and 12. The number of elements of order 2, 3, 4, 6, 12, are φ(1)= 1 (0), φ(2)= 1 (6, |⟨6⟩| = 2), φ(3)= 2 (4, 8), φ(4)= 2 (3, 9), φ(6)= 2 (2, 10), φ(12)= 4 (1, 5, 7, 11) respectively (Figure 1.a.)

• ℤ₂₄. Order of subgroups are: 1, 2, 3, 4, 6, 8, 12, and 24. Let’s list all generators for the subgroup of order 8.

⟨n/k⟩ is the unique subgroup of ℤ_n of order k. ⟨24/8⟩=⟨3⟩ is the unique subgroup of ℤ₂₄ of order 8. 3 is obviously a generator, but it does not need to be the only one. ⟨3⟩=⟨3j⟩, 3j is a generator of a group of order 8 of ℤ₂₄ where 24/gcd(8, j) = 24, that is, gcd(8, j) = 1, so 3 (j=1), 9(j=3), 15(j=5), 21(j=7). ⟨3⟩=⟨9⟩=⟨15⟩=⟨21⟩ = {3, 6, 9, 12, 15, 18, 21, 1}. There are four generators for the unique subgroup of ℤ₂₄ of order 8, φ(8) = 4.

To sum up, in ℤ₂₄, the number of elements of order 8 is φ(8) = 4. They are ⟨3⟩=⟨9⟩=⟨15⟩=⟨21⟩ = {3, 6, 9, 12, 15, 18, 21, 1}.

• ℤ₃₀. Order of subgroups are: 1, 2, 3, 5, 6, 10, and 15. The number of elements of order 1, 2, 3, 5, 6, 10, and 15, are φ(1)= 1 (0), φ(2)= 1 (15), φ(3)= 2 (10, 20), φ(5)= 4 (6, 12, 18, 24), φ(6)= 2 (5, 25), φ(10)= 4 (3, 9, 21, 27) respectively (Figure 1.c.)

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.