Computing Galois group II. Determine Galois and normal extension.

There is nothing more practical than a good theory, Leonid Brezhnev.

Recall

Theorem. Let K/F be a finite extension. The following statements are equivalent:

1. K/F is Galois.
2. F is the fixed field of Aut(K/F), i.e., F = K^Gal(K/F)
3. A finite extension K/F is Galois iff the order of the Galois group equals the degree of the extension, i.e., |Gal(K/F)| = [K : F]
4. K/F is a normal, finite, and separable extension.
5. K is the splitting field of a separable polynomial f ∈ F[x] over F.
6. Let Char(F)=0 or F be finite (or more generally F is perfect). Then, a finite extension K/F is Galois if and only if K/F is normal.

Fundamental Theorem of Galois Theorem. Let K/F be a finite separable extension, i.e., a Galois extension. Let G = Gal(K/F) be the Galois group. Then, the following statements holds, (1) There is an inclusion-reversing bijective map or correspondence from subgroups of G and intermediate fields of K/F, given by H → K^H, its inverse is defined by L → Gal(K/L). H₁ ⊇ H₂ ⇒ K^H₁ ⊆ K^H₂ and L₁ ⊆ L₂ ⇒ Gal(K/L₁) ⊇ Gal(K/L₂). Futhermore, it satisfies the following equality |H| = [K : K^H] and [G : H] = [K^H : F]

(2) Suppose an intermediate field L (F ⊆ L ⊆ K) corresponds to the subgroup H under the Galois correspondence. K/L is always normal (hence Galois). L is Galois over F if and only if H = Gal(K/L) is a normal subgroup of G, H = Gal(K/L) ◁ G In this case, the Galois group of L/F is isomorphic to the quotient group G/H, i.e., Gal(L/F) ≋ G/Gal(K/L)

• $K = \mathbb{Q}(\sqrt{3},\sqrt{5})$, $σ: \sqrt{3} → -\sqrt{3}, τ: \sqrt{5} → -\sqrt{5}, μ = στ: \sqrt{3} → -\sqrt{3}, \sqrt{5} → -\sqrt{5}, \sqrt{15} → \sqrt{15}$. Gal($\mathbb{Q}(\sqrt{3},\sqrt{5})/\mathbb{Q}$) = {id, σ, τ, μ} ≋ ℤ/ℤ₂xℤ/ℤ₂. Then, G = Gal(K/F), [K/F is Galois if F = K^G] Gal(K/K^G) = Gal($\mathbb{Q}(\sqrt{3},\sqrt{5})/ℚ$) and the extension is obviously Galois.

  [K: ℚ] = 4, and K as a vector space over ℚ has a basis {$1, \sqrt{3}, \sqrt{5}, \sqrt{15}$} and dim_ℚK = 4, so every element a ∈ K can be written uniquely as $a + b\sqrt{3} + c\sqrt{5} + d\sqrt{15}$. σ is defined uniquely as $a + b\sqrt{3} + c\sqrt{5} + d\sqrt{15} → a - b\sqrt{3} + c\sqrt{5} - d\sqrt{15}$, τ: $a + b\sqrt{3} + c\sqrt{5} + d\sqrt{15} → a + b\sqrt{3} - c\sqrt{5} - d\sqrt{15}$, μ: $a + b\sqrt{3} + c\sqrt{5} + d\sqrt{15} → a - b\sqrt{3} - c\sqrt{5} + d\sqrt{15}$

Why [K : ℚ] = 4? We build the tower, $\mathbb{Q} ⊆ \mathbb{Q}(\sqrt{3}) ⊆ \mathbb{Q}(\sqrt{3}, \sqrt{5})$. A) $\sqrt{3}∉\mathbb{Q}$, x² -3 is irreducible in ℚ, and degree(x²-3) = 2 ⇒ [$\mathbb{Q}(\sqrt{3}) : \mathbb{Q}$] = 2. B) $\sqrt{5}∉\mathbb{Q}(\sqrt{3})$, x² -5 is irreducible in $\mathbb{Q}(\sqrt{3})$, and degree(x²-5) = 2 ⇒ [$\mathbb{Q}(\sqrt{3}, \sqrt{5}):\mathbb{Q}(\sqrt{3})$] = 2 ⇒ C) [K : ℚ] = [$\mathbb{Q}(\sqrt{3}, \sqrt{5}):\mathbb{Q}(\sqrt{3})$][$\mathbb{Q}(\sqrt{3}) : \mathbb{Q}$] = 2·2 = 4

K/ℚ is normal. Then K/ℚ is a finite normal extension if and only if it is the splitting field of some polynomial f(x) ∈ K[x]. It suffices to consider f(x) = (x² -3)(x² -5). Its splitting field must contain $\sqrt{3}$ and $\sqrt{5}$ and since K is the smallest field containing both of them, K must be in fact the splitting field of f(x) ⇒ K is normal over ℚ.

• A completely similar argument as a previous example shows that $K = \mathbb{Q}(\sqrt{2},\sqrt{3})$, $σ: \sqrt{2} → -\sqrt{2}, τ: \sqrt{3} → -\sqrt{3}, μ = στ: \sqrt{2} → -\sqrt{2}, \sqrt{3} → -\sqrt{3}, \sqrt{6} → \sqrt{6}$. Gal($\mathbb{Q}(\sqrt{2},\sqrt{3})/\mathbb{Q}$) = {id, σ, τ, μ} ≋ ℤ/ℤ₂xℤ/ℤ₂. Then, G = Gal(K/F) = [K/F is Galois if F = K^G] Gal(K/K^G) = Gal($\mathbb{Q}(\sqrt{2},\sqrt{3})/ℚ$) and the extension is obviously Galois.

Futhermore, K has 3 subfields L such that [K : L] = 2 (⇒ [L : ℚ] = 2), namely $ℚ(\sqrt{2}),ℚ(\sqrt{3}),ℚ(\sqrt{6})$, and $\mathbb{Q}(\sqrt{2},\sqrt{3})=\mathbb{Q}(\sqrt{2} +\sqrt{3})$

K/ℚ is normal. Then K/ℚ is a finite normal extension if and only if it is the splitting field of some polynomial f(x) ∈ K[x]. It suffices to consider f(x) = (x² -2)(x² -3). Its splitting field must contain $\sqrt{2}$ and $\sqrt{3}$ and since K is the smallest field containing both of them, K must be in fact the splitting field of f(x) ⇒ K is normal over ℚ.

• Let K = $\mathbb{Q}(\sqrt[3]{2}, w)$, F = ℚ, and w is the primitive third root of unity $w = e^\frac{2πi}{3}$

  Reclaim: Any degree 2 extension is normal, but it does not necessarily have to be Galois.

[$\mathbb{Q}(\sqrt[3]{2}, w): \mathbb{Q}$] = 2 · 3 = 6. We know K is the splitting field of x³ - 2 over ℚ (the roots are $\sqrt[3]{2}, \sqrt[3]{2}w, \sqrt[3]{2}w^2$, they are all in K and if you remove any of them, you don’t get K, it is generated by all its roots) ⇒ K/ℚ is normal.

The possible images of $\sqrt[3]{2}$ are $\sqrt[3]{2}, \sqrt[3]{2}w, \sqrt[3]{2}w^2$, and w can be mapped to w and w². There exists a homomorphism K → K for every choice of images $\sqrt[3]{2}$ and w, so there are 6 (3 x 2 choices) automorphism K → K, |Gal(K/ℚ)| = 6 = [K : ℚ] ⇒ K/ℚ is Galois

$\sqrt[3]{2}$ and w are linear independent, and their images are to be chosen independently (the conjugates of a root, say α, are the images of α under the field homomorphism) of each other because $\sqrt[3]{2}$ ∈ ℝ, and w is not real. Futhermore, there exists a homomorphism K → K for every choice of images of w and $\sqrt[3]{2}$, it will send any root to one of its conjugates.

Finally, what is Gal(K/ℚ)? There are only two groups of order 6 up to isomorphism, namely the cyclic group ℤ/6ℤ (Abelian), and the symmetric group of order 3, S₃.

• σ₀: $\sqrt[3]{2}→\sqrt[3]{2}$, w → w.
• σ₁: $\sqrt[3]{2}→\sqrt[3]{2}w$, w → w.
• σ₂: $\sqrt[3]{2}→\sqrt[3]{2}w^2$, w → w.
• σ₃: $\sqrt[3]{2}→\sqrt[3]{2}$, w → w².
• σ₄: $\sqrt[3]{2}→\sqrt[3]{2}w$, w → w².
• σ₅: $\sqrt[3]{2}→\sqrt[3]{2}w^2$, w → w².

σ₄∘σ₅ = σ₂ ≠ σ₁ = σ₅∘σ₄ ⇒ Gal(K/ℚ) is not Abelian ⇒ Gal(K/ℚ) ≋ S₃

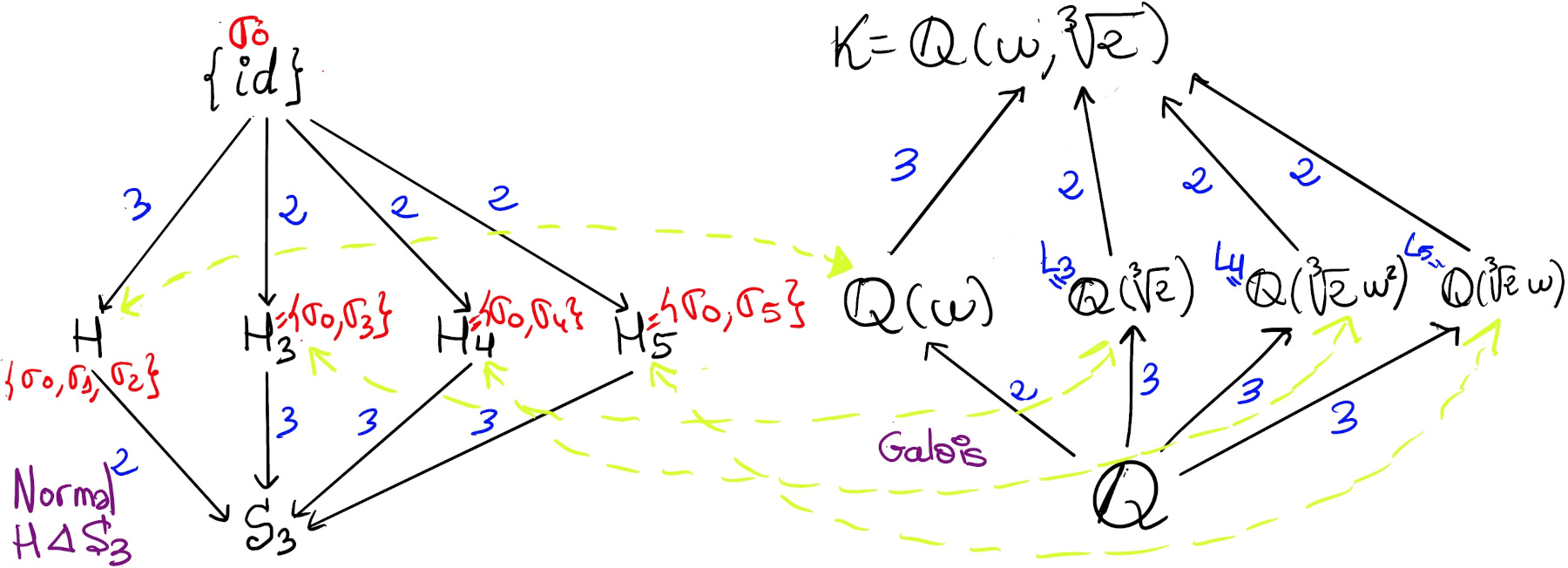
Let’s have a look at the subgroups. The trivial subgroups are S₃ (whose extension is ℚ) and {σ₀ = id} (whose extension is K). The order of the proper subgroups can only be a divisor of 6 by Lagrange’s Theorem, so we are left with 2 or 3.

It is left to the reader to check that σ₃² = σ₄² = σ₅² = σ₀

Therefore, we have the following subgroups of order 2, namely H₃ = {σ₀, σ₃}, H₄ = {σ₀, σ₄}, and H₅ = {σ₀, σ₅}. None of them are normal (H◁G iff ∀g ∈ G, gNg^-1 ⊆ N), e.g., H₄ is not normal because σ₅∘σ₄∘σ₅^-1 = [σ₅² = σ₀ = id] σ₅∘σ₄∘σ₅ = σ₁∘σ₅ = σ₅ ∉ H₄. Therefore, the corresponding field extensions (L_i is the extension whose Galois group is H_i) are not Galois.

Notice that $σ_3(\sqrt[3]{2}) = \sqrt[3]{2} ⇒ ℚ(\sqrt[3]{2}) ⊆ L_3$

Therefore, $ℚ(\sqrt[3]{2}) ⊆ L_3$ and [L₃ : $ℚ(\sqrt[3]{2})$] = 1 ⇒ L₃ = $ℚ(\sqrt[3]{2})$. Following a similar argument, we can demonstrate that L₄ = $ℚ(\sqrt[3]{2}w^2)$ (Notice: $σ_4(\sqrt[3]{2}w^2) = \sqrt[3]{2}ww^4 = \sqrt[3]{2}w^2$), and L₅ = $ℚ(\sqrt[3]{2}w)$ ($σ_5\sqrt[3]{2}w = \sqrt[3]{2}w^2w^2 = \sqrt[3]{2}w$). In fact, these three extensions are isomorphic because they adjoin roots to ℚ of the same irreducible polynomial (x³ -2), that is, ℚ(α₁) ≋ ℚ(α₂) ≋ ℚ(α₃) ≋ ℚ[x]/⟨x³ -2⟩.

As for subgroups of order 3 (they are isomorphic to ℤ₃), we just need to find non trivial elements of order 3. It is left to the reader to show that σ₁ and σ₂ are elements of order 3, σ₁∘σ₂ = σ₂∘σ₁ = σ₀, so we have only one subgroup of order 3, namely, L = {σ₀, σ₁, σ₂}. σ_i(w) = w, 0 ≤ i ≤ 2 ⇒ ℚ(w) ⊆ L

Therefore, L = ℚ(w). Futhermore, since H ◁ G (all subgroups of index 2 are normal) ⇒ ℚ(w)/ℚ is a Galois extension (the splitting field of a separable polynomial x² +x +1). The following are two diagrams with the subgroups of S₃ ≋ Gal(K/ℚ) and their corresponding fixed fields.

• Let K = $\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})$, F = ℚ. Computing Gal(K, ℚ) is relatively easy, it is Gal(K, ℚ) = ⟨σ₂, σ₃, σ₅⟩ with σ_k the automorphism K → K that interchanges $\sqrt{k}→-\sqrt{k}$ (k = 2, 3, and 5) and does not move the rest of the elements. A far more detail explanation is given in Consequences Galois III. Exercises. ℚ(√2+√3+√5)

Gal(K, ℚ) = ⟨σ₂, σ₃, σ₅⟩ ≋ ℤ/2ℤ x ℤ/2ℤ x ℤ/2ℤ. You can think (a, b, c) ∈ ℤ/2ℤ x ℤ/2ℤ x ℤ/2ℤ as representing $\sqrt{2}→(-1)^a,\sqrt{3}→(-1)^b, \sqrt{5}→(-1)^c$.

K/ℚ is a Galois extension (normal and separable) since K is the splitting field of the polynomial (x² -2)(x² -3)(x² -5) and ℚ is the base field (char(ℚ) = 0). Another way of seeing this is [K : ℚ] = 8 = |Gal(K/ℚ)|.

Fact: The square roots of different primes are linearly independent over the field of rationals

• Let K = $\mathbb{Q}(\sqrt[4]{2})$, F = ℚ. [K : F] = 4. It is not normal, f(x) = x⁴ -2 has a root but not all of them ($±\sqrt[4]{2}, ±\sqrt[4]{2}i$) since K ⊆ ℝ. Futhermore, possible images of $\sqrt[4]{2}$ in K are $\sqrt[4]{2}, -\sqrt[4]{2}$, so there are only two possibilities: identity, σ: $\sqrt[4]{2} → -\sqrt[4]{2}$ ⇒ [K : ℚ] = 4 > |Gal(K/ℚ)| = 2 ⇒ K/ℚ is not Galois, Gal(K/ℚ) ≋ ℤ/ℤ₂

What is K^Gal(K/ℚ). We know [K : K^Gal(K/ℚ)] = |Gal(K/ℚ)| = 2

Since [K : ℚ] = 4 ⇒ [K^Gal(F/ℚ) : ℚ] = 2.

Notice that $σ(\sqrt{2}) = σ(\sqrt[4]{2}\sqrt[4]{2})= σ(\sqrt[4]{2})^2 = (-\sqrt[4]{2})^2 = \sqrt{2} ⇒\sqrt{2}$ is fixed by 1 and σ ⇒ $\mathbb{Q}(\sqrt{2})⊆\mathbb{K}^{Gal(\mathbb{K}/\mathbb{Q})}$

$\mathbb{Q}(\sqrt{2})⊆\mathbb{K}^{Gal(\mathbb{K}/\mathbb{Q})}$ ⇒ $\mathbb{Q}(\sqrt{2})=\mathbb{K}^{Gal(\mathbb{K}/\mathbb{Q})}$

• Let p be a prime number, r a positive integer, r ≥ 1, $K=\mathbb{F}_{p^r}, F = \mathbb{F}_p,$ [K : F] = r.

F finite, p = char(F) > 0. [Classification of finite fields. Let F be a finite field of order q = p^r. Then, K is the splitting field of the polynomial x^q-x ∈ $\mathbb{F}_p[x]$.] K is the splitting field of $x^{p^{r}}-x~ over~ \mathbb{F_p}$ ⇒ the extension is normal.

Let σ: K → K, σ(α) = α^p, σ is a field homomorphism (x + y)^p = x^p + y^p because when p is prime ⇒ p | ${p \choose k}$, injective ⇒ If a set X is finite, an injective map f: X → X is also surjective. Futhermore, σ(a) = a ∀a ∈ F_p ⇒ σ is an F-automorphism of K, i.e., σ ∈ Gal(K/F).

σ is injective because F field, Φ: F→ F, Ker(Φ) is an ideal of F, a field ⇒ KerΦ={e} or KerΦ = F ⇒ Φ is 1-1 because ker(Φ) is the trivial ideal, or Φ is zero (⊥ because ker(Φ) = F).

Notice σ²(α) = σ(σ(α)) = σ(α^p) = (α^p)^p = $α^{p^{2}}, σ^i(α)=α^{p^{i}}$ ∀α ∀i ≥ 1

Let’s suppose order of σ is n, σⁿ = id, i.e, σⁿ(α) = α ∀α ∈ K ⇒ $σ^n(α)=α^{p^{n}}=α$ ⇒ ∀α ∈ K, α is a root of f(x) = $x^{p^{n}}-x$ in K. Since deg(f(x)) = pⁿ, f(x) has at most pⁿ roots. However, every element of K is a root of f ⇒ |K| = p^r ≤ pⁿ ⇒ r ≤ n.

Theorem. A polynomial f of degree n over a field F has at most n roots in F.

Futhermore, [Classification of finite fields. Let F be a finite field of order q = p^r. Then, F is the splitting field of the polynomial x^q-x ∈ $\mathbb{F}_p[x]$. K is the splitting field of $x^{p^{r}}-x~ over~ \mathbb{F_p}$] $σ^r(α)=α^{p^{r}}=α$ ⇒ σ^r = 1 ⇒ order(σ) ≤ r ⇒ n = r ⇒ The subgroup generated by σ in $Gal(\mathbb{F_{p^r}}/\mathbb{F_p})$ = {1, σ, σ²,···, σ^r-1} has order r ⇒ $|Gal(\mathbb{F_{p^r}}/ \mathbb{F_p})|$ ≥ r.

$r = [\mathbb{F_{p^r}} : \mathbb{F_p}] ≥ [F_{p^r} : F_{p^r}^G] = |Gal(\mathbb{F_{p^r}}/ \mathbb{F_p})|≥ r ⇒ [\mathbb{F_{p^r}} : \mathbb{F_{p^r}^G}] = r~ and~ [F_{p^r}^G : \mathbb{F_p}] = 1 ⇒ \mathbb{F_{p^r}^G} = \mathbb{F_p} ⇒ \mathbb{F_{p^r}}/ \mathbb{F_p}$ is Galois.

Futhermore, $Gal(\mathbb{F}_{p^r}/ \mathbb{F}_p)≋ℤ/rℤ$ because we have already found an automorphism of order r, so it is cyclic.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).