Coding Theory

Whatsoever thy hand findeth to do, do it with thy might; for there is no work, nor device, nor knowledge, nor wisdom, in the grave, whither thou goest, Ecclesiastes 9:10.

Coding Theory is the use of algebraic techniques to protect data transmission affected by noise, e.g., human error, imperfect or noisy channels, interference, etc.

The communication that occurs in our day-to-day life is in the form of signals. These signals, such as sound signals, generally, are analog in nature. However, digital communications are often transmitted as a sequence of binary numbers.

When the communication needs to be established over a distance, then the analog signals are sent through wire. The conventional methods of communication used analog signals for long distance communications, which suffer from many losses such as distortion, interference, and security breaches.

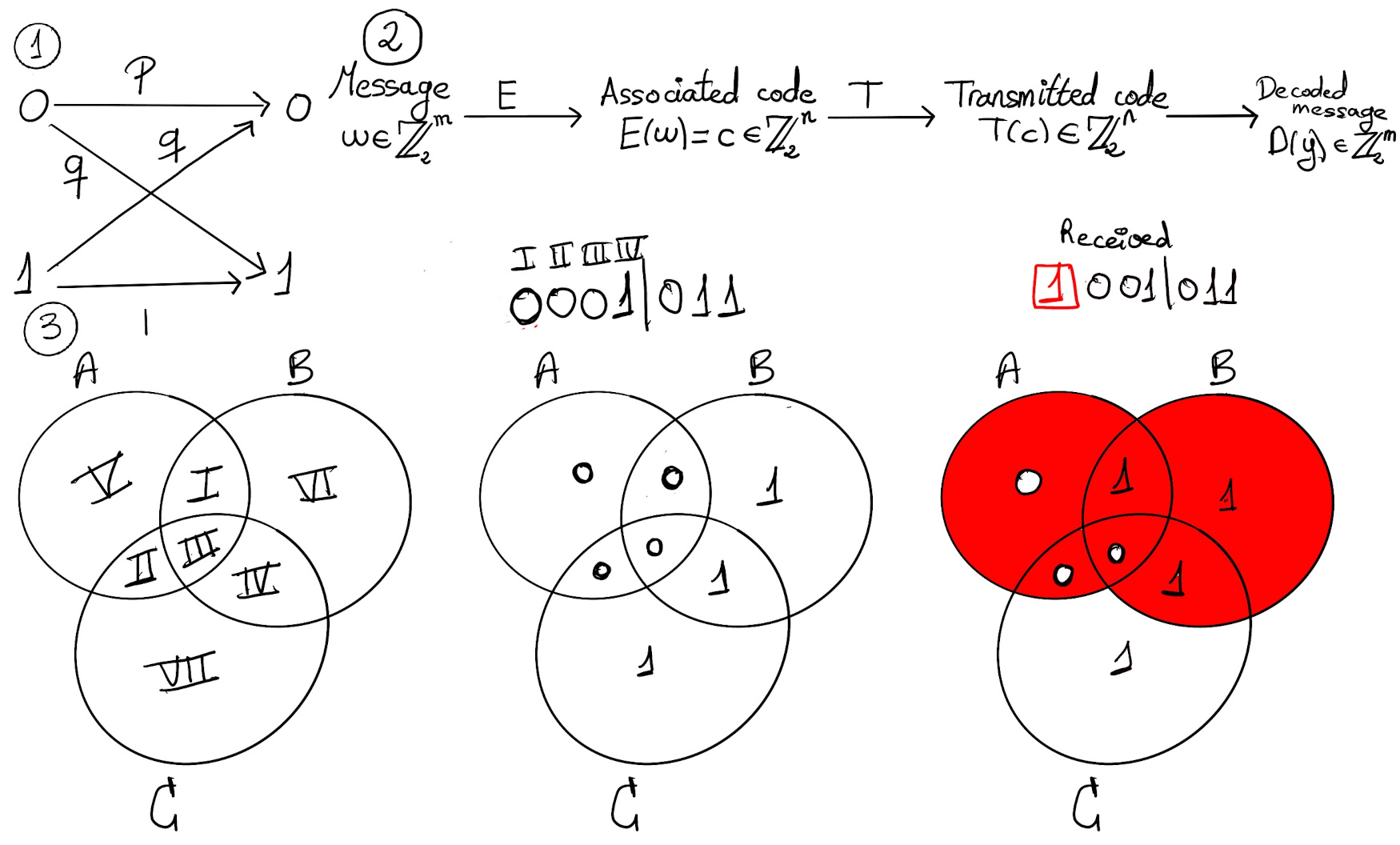
A binary symmetric channel T is a model used in coding theory. In this model, a transmitter wishes to send a binary signal, and the receiver will receive a bit. Let p be the probability that a bit is transmitted correctly, and q = 1-p is the probability that a bit is flipped, that is, transmitted incorrectly (Figure 1).  

This is an example of a Bernoulli trial, that is, a random experiment with exactly two possible outcomes, “success” and “failure”, in which the probability of success is the same every time the experiment is conducted.

Let X be the random variable which counts the number of failures, the probability that k errors will occur if n bits are transmitted through the binary symmetric channel T is: $P(X=k)={n \choose k}p^{n-k}q^k$

Example. Let p = 0.995, n = 500, that is, the message is 500 bits long:

• What is the probability that the message is sent without any errors? $P(X=0)={500 \choose 0}0.995^{500}(0.005)^0≈0.08157$
• What is the probability that the message is sent with at least one error, i.e., one error or more? $1-P(X=0)≈0.91842$
• What is the probability that the message is sent with exactly one error? $P(X=1)={500 \choose 1}0.995^{499}(0.005)^1≈0.20495$
• What is the probability that the message is sent having one or two errors? P(1 ≤ X ≤ 2) = P(X = 1) + P(X = 2). What is the probability that the message is sent having more than two errors? P(X > 2) = 1 - P(X = 0) - P(X =1) - P(X =2), and so on.

A sequence of m-bits b₁b₂…b_m can be identified naturally with the m-tuple (b₁, b₂, …, b_m) ∈ $ℤ_2^m$

An (n, m)-block code C could be understood as a subset of $ℤ_2^n$ paired with two functions E: $ℤ_2^m → ℤ_2^n$ and D: $ℤ_2^n → ℤ_2^m$, called the encoding and decoding function respectively, such that E is injective, D∘E = $Id_{ℤ_2^m}$, and $E(ℤ_2^m)=C.$ We call the elements of C codewords.

This is the typical model of communication system (Figure 2):  

Ideally, D∘T∘E = $Id_{ℤ_2^m}$, but it will not always be possible since T is not a mathematical function, but typically there would be some errors or random noise.

A k-error detecting code is a code which reports an error when D∘T∘E ≠ $Id_{ℤ_2^m}$ for k or fewer errors, but there is no guarantee to correct those errors. An l-error correcting code is a code for which D∘T∘E = $Id_{ℤ_2^m}$ even in the presence of l or fewer errors.

ASCII

ASCII, abbreviated from American Standard Code for Information Interchange, is a character encoding standard for electronic communication. It is an (8, 7)-block code, yielding 2⁸ possible codewords.

Originally based on the English alphabet, ASCII encodes 128 characters into seven-bit integers. Most of the encoded characters are printable and include the digits, lowercase letters a to z, uppercase letters A to Z, and punctuation symbols. The eight bit, placed on the left, is called the parity check bit, and it is the sum of the other seven bits modulo n.

The mappings E: ℤ₂⁷ → ℤ₂⁸, E(b₁, b₂,…b₇) = (b₁ + b₂ + …+ b₇ (mod 2), b₁, b₂,…b₇), D: ℤ₂⁸ → ℤ₂⁷, D(c₁, c₂,…c₈) = (c₂, c₃,…c₈) are the encoding and decoding mapping respectively. ASCII forms a code which can detect a single error in a transmission. Unfortunately, this code cannot detect the presence of two or more error.

Let’s see ASCII in action. Let E(w) = 0100 0001 = c, T(c) = 0100 1001, then we have an even number of ones (“3”), but the parity check bit is a zero!!! However, T(c) = 0100 1101 is also incorrect, but the code is unable to detect it 😞

• The triple repetition code is one of the most basic error-correcting codes. In order to transmit a message over a noisy channel, the idea is to just repeat the message three times. The mappings E: ℤ₂^m → ℤ₂^3m, E(b₁, b₂,…b_m) = (b₁, b₂,…b_m, b₁, b₂,…b_m, b₁, b₂,…b_m), D: ℤ₂^3m → ℤ₂^m, D(c₁, c₂,…c_3m) = (c₁, c₂,…c_m) are the encoding and decoding mapping respectively.

This (3m, m)-block code is a 1 error correcting code, and if there is an error with a bit, the code can correct itself by checking and outputting the most common value. However, because of its low code rate (ratio between useful information or data and actual transmitted symbols) and the fact that it cannot detect nor correct if two or more errors occur for the same bit, other error correction codes are preferred in most cases.

The Hamming Metric

The Hamming (7, 4) code. A message consists of all possible 4-tuples of 0s and 1s, (x₁, x₂, x₃, x₄). Encoding will be done by multiplying each of this messages (2⁴ = 16) on the right (these messages will be interpreted as 1 x 4 matrices with entries from ℤ₂) by the matrix G, that is possible since 1 x 4 · 4 x 7 = 1 x 7.

$[ \left( \begin{smallmatrix}x_1& x_2& x_3& x_4\end{smallmatrix} \right) G = \left(\begin{smallmatrix}x_1& x_2& x_3& x_4\end{smallmatrix} \right)\left( \begin{smallmatrix}1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right) ]$

Examples:

$[ \left(\begin{smallmatrix}0 & 0 & 0 & 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right) = \left(\begin{smallmatrix}0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right), \left(\begin{smallmatrix}0 & 0 & 1 & 0\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right) = \left(\begin{smallmatrix}0 & 0 & 1 & 0 & 1 & 1 & 1\end{smallmatrix} \right), \left(\begin{smallmatrix}0 & 1 & 1 & 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right) = \left(\begin{smallmatrix}0 & 1 & 1 & 1 & 0 & 0 & 1\end{smallmatrix} \right) ]$

The reader should take into consideration that:

1. All calculations are done modulo 2.
2. The resulting 7-tuples are called code words.
3. The first four digits of each code words is the original message (the first 4 columns of G is just the identity matrix).
4. The last three digits corresponds to the redundancy features. It uses the nearest-neighbor decoding message, that is, for any received word v, it is assumed that the word sent is the code word v' that differs from v in the fewest number of positions, e.g., 1001011 (there is an error in the first bit) would still be decoded as 0001011
5. The decoding function is pretty simple. It takes v = (v₁, v₂, …, v₇) as an argument, and deletes the last three digits, (v₁, v₂, v₃, v₄).

This code can be illustrated with Venn diagrams. Begin by placing the four message digits in the four regions I, II, III, and IV, with the digit in position 1 in region 1 (e.g., 0), the digit in position 2 in region 2 (e.g., 0), and so on. V, VII, and VII are assigned 0s or 1s so that the number of 1s in each circle is even.  

When there is an error (e.g., 1001011), we can detect that the regions A and B have an odd number of ones, e.g., the regions A and B have 1 and 3 respectively number of ones.

Definition. An (n, k) linear code over a finite field F is a k-dimensional subspace V of the vector space Fⁿ = F ⊕ F ⊕ ··· ⊕ F such that the elements in V are the code words. When F is ℤ₂, we have a binary code.

An (n, k) linear code over F (say F is a finite field of order q, |F| = q) is a set of n-tuples consisting of two parts: the message part (k digits, so we have q^k code words since every element of the code is uniquely expressed as a linear combination of the k basis vectors with coefficients from F) + the redundancy part (n -k remaining digits).

Examples: The Hamming (7, 4) is a binary code, the set {0000, 0101, 1010, 1111} is a (4,2) binary code. The set {0000, 0121, 0212, 1022, 1110, 1201, 2011, 2102, 2220} is a (4,2) linear code over ℤ₃.

The Hamming distance between two vectors in Fⁿ is the number of components in which they differ. In particular, x, y ∈ ℤ₂ⁿ, the Hamming distance between x and y is the number of positions or bits in which x and y differ, e.g., x = 0011, y = 1010, its Hamming distance is d(x, y) = 2.

The Hamming weight of a vector wt(u), u ∈ Fⁿ is the number of nonzero entries in u. In particular, the weight of x in ℤ₂ⁿ, denoted by w(x), is the total number of 1’s in x (1 is the only symbol that is different from 0 in ℤ₂), e.g., w(x) = w(y) = 2. Futhermore, d(u, v) = wt(u-v) (d(u, v) and wt(u-v) both equal the number of positions in which u and v differ).

The Hamming weight of a linear code is the minimum weight of any nonzero vector in the code. The minimum distance of a code C, denoted d_min is the minimum of all Hamming distances d(x, y) where x and y are distinct codewords in C.

Example. The Hamming distance of a code. Consider the code = {c₀, c₁, c₂, c₃}, where c₀ = (000000), c₁ = (101101), c₂ = (010110), c₃ = (111011). This code has a minimum distance d = 3 because 3 = min{d(c₀, c₁), d(c₀, c₂), d(c₀, c₃), d(c₁, c₂), d(c₁, c₃), d(c₂, c₃)} = min{4, 3, 5, 5, 3, 4}. Futhermore, w(c₀) = 0, w(c₁) = 4, w(c₂) = 3, w(c₃) = 5.

Definition. A metric space is an ordered pair (M, d) where M is a set and d is a metric on M, i.e., a function d: M x M → ℝ, satisfying the following axioms ∀x, y, z ∈ M,

1. The distance from a point to itself is zero, d(x, x) = 0.
2. Positivity. The distance between two distinct points is always positive. If x ≠ y ⇒ d(x, y) > 0
3. Symmetry. The distance from x to y is always the same as the distance from y to x, d(x, y) = d(y, x)
4. The triangle inequality holds, d(x, z) ≤ d(x, y) + d(y, z).

Theorem. The Hamming distance is a metric (a distance function) in F_n.

Proof.

1. d(u, v) ≥ 0, with equality d(u, v) = 0 ↭ u - v = 0 ↭ u = v
2. d(u, v) = d(v, u)
3. d(u, w) = wt(u -w) ≤ wt(u -v) + wt(v -w) = d(u, v) + d(v, w).

To see that wt(u -w) ≤ wt(u -v) + wt(v -w), realize that if (for any arbitrary i) u_i, w_i are different (u and w differ in the ith position), then u_i, v_i or v_i, w_i are different (otherwise, u_i=v_i and v_i=w_i ⇒ u_i=w_i ⊥)

Theorem. Suppose the Hamming weight of a linear code is at least 2t + 1. Then, it can correct any t or fewer errors. Futhermore, it can be used to detect 2t or few errors.

Proof.

We are going to use the nearest neighbor decoding. Suppose u is transmitted and v is received. Decode it as the nearest code word, that is, we will assume that the corresponding code word sent is a code word v’ such that the Hamming distance d(v, v’) is a minimum.

If there is more than one such v’, do not decode. There are too many errors.

Suppose that there is no more than t errors, so that d(u, v) ≤ t. Let w be a code word other than u.

[By assumption, the Hamming weight of the linear code is at least 2t + 1, that is, ∀u, w, u ≠ w] 2t + 1 ≤ d(u, w) ≤ d(u, v) + d(v, w) ≤ [We are supposing that there is no more than t errors] t + d(v, w) ⇒ t + 1 ≤ d(v, w) ⇒ If w is a code word other than u (u ≠ w), d(v, w) > t, but d(u, v) ≤ t that is, the closest word to the received v is u, and v is correctly decoded as u.

Futhermore, if u is transmitted as v with at least one error, but fewer than 2t error, then it cannot be another code word since d(u, v) ≤ 2t and, by assumption, the minimum distance between distinct code words is at least 2t + 1. Because only code words are transmitted, errors will be detected whenever a received word is not a code word.

Remark. Suppose the Hamming weight of a linear code is at least 2t + 1. We can correct any t or fewer errors or detect 2t or few errors, but we cannot use it to do both simultaneously, e.g., the Hamming (7, 4) code’s weight is 3 = 2·1 + 1, t = 1, so we may decide either to detect any one or two errors and refuse to code or correct and decode any single error.

Suppose that we receive 1101011, there are two options:

1. If we want error detection, we can tell this is not a correct message, so we simply refuse to code.
2. If we want error correction, we would assume (maybe we would be wrong, and it was 0001011 because there were two errors in the transmission) that there was only one error, so the code word is 1100011.

Systematic code

We encode a word (x₁···x_k) as

$[ \left( \begin{smallmatrix}x_1& x_2& ···& x_k\end{smallmatrix} \right) G = \left(\begin{smallmatrix}x_1& x_2& ···& x_k\end{smallmatrix} \right)\left( \begin{smallmatrix}1 & 0 & ··· & 0 | & a_{11} & ··· & a_{1n-k}\\ 0 & 1 & ··· & 0 | & a_{21} & ··· & a_{2n-k}\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\ 0 & 0 & ··· & 1 | & a_{k1} & ··· & a_{kn-k}\end{smallmatrix} \right) ]$ where G = {I_k | A}. It carries a subspace V of F^k to a subspace of Fⁿ, and the vector vG will agree with v in the first k components and will use the last n-k components to create some redundancy for error detection or correction.

In other words, the first k digits are the message digits. Such an (n, k) linear code is called a systematic code, and the matrix is called the standard generator matrix.

Examples.

• From the set of messages (x₁, x₂, x₃) ∈ ℤ₂³, we may construct a linear code with the standard generator matrix G and get the resulting code words {000000, 001111, 010101, 100110, 110011, 101001, 011010, 111100}. 000 (message) → 000000 (code word), 001 → 001111, 010 → 010101, etc.

$[ \left( \begin{smallmatrix}x_1& x_2& x_3\end{smallmatrix} \right) G = \left(\begin{smallmatrix}x_1& x_2& x_3\end{smallmatrix} \right)\left( \begin{smallmatrix}1 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 1 & 1 & 1\end{smallmatrix} \right) ]$

The reader should realize that all nonzero code words have weight at least 3 ⇒[Theorem. Suppose the Hamming weight of a linear code is at least 2t + 1. Then, it can correct any t or fewer errors. Futhermore, it can be used to detect 2t or few errors. t = 1] It will correct single errors or detect up to two errors.

• From the set of messages {00, 01, 02, 10, 11, 12, 20, 21, 22}, we may construct a linear code with the standard generator matrix G and get the resulting code words, {0000, 0122, 0211, 1021, 1110, 1202, 2012, 2101, 2220}, e.g., 00 → 00, 01 → 0122, 02 → 0244 →ℤ₃ 0211, etc.

$[ \left( \begin{smallmatrix}x_1& x_2\end{smallmatrix} \right) G = \left(\begin{smallmatrix}x_1& x_2\end{smallmatrix} \right)\left( \begin{smallmatrix}1 & 0 & 2 & 1\\0 & 1 & 2 & 2\end{smallmatrix} \right) ]$

All nonzero code words have weight at least 3 ⇒ It will correct single errors or detect up to two errors.

Parity-Check Matrix Decoding

Suppose that V is a systematic linear code over the field F given by the standard generator matrix G = $\left( \begin{smallmatrix}1 & 0 & ··· & 0 | & a_{11} & ··· & a_{1n-k}\\ 0 & 1 & ··· & 0 | & a_{21} & ··· & a_{2n-k}\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\ 0 & 0 & ··· & 1 | & a_{k1} & ··· & a_{kn-k}\end{smallmatrix} \right)$ = [I_k | A], I_k is the identity matrix k x k. Let H = [$\begin{smallmatrix}-A\\ I{n-k}\end{smallmatrix}$] be the parity-check matrix for V.

The decoding algorithm is as follows:

1. If w is received, compute wH.
2. is wH the zero vector? If wH = 0 ⇒ We assume no errors took place during the transmission 😀, good!
3. If there is exactly one instance of a non-zero element of the field, say s ∈ F*, such that wH equals s times the ith row of H, then decode w as w - se_i where e_i is the ith row of I_n = w - (0 ··· s_{ith component or position} ··· 0). If there is more that one such instance, do not decode. If the code is binary, we simply change the ith position of w.
4. If the last two cases do not happen, assume more than two error occur, and do not decode.

Example. Let us consider the Hamming (7, 4) code given by the standard generator matrix $G = \left( \begin{smallmatrix}1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1 & 1\end{smallmatrix} \right)$ and the corresponding parity-check matrix, $H = \left( \begin{smallmatrix}-A\\ I{n-k}\end{smallmatrix} \right) = \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right)$

If w = 0000110 is received, then $wH = \left( \begin{smallmatrix}0\\ 0\\ 0\\ 0\\ 1 \\ 1\\ 0\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 1\\ 0\end{smallmatrix} \right)$ is the first row of H ⇒ [We assume that an error has occurred in the transmission in the first position of v] we decode it as (000110) - (1000000) = 1000110 ⇒ The original message is 1000.

If w = 1011111 is received, then $wH = \left( \begin{smallmatrix}1\\ 0\\ 1\\ 1\\ 1 \\ 1\\ 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 0\\ 1\end{smallmatrix} \right)$ is the second row of H ⇒ [We could assume that an error has occurred in the transmission in the second position of v] we decode it as (1011111) - (0100000) = 1111111 ⇒ The original message is 1111.

If u = 1001101 is sent, and z = 1001011 is received ⇒$zH = \left( \begin{smallmatrix}1\\ 0\\ 0\\ 1\\ 0 \\ 1\\ 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 1\\ 0\end{smallmatrix} \right)$, the first row. We will wrongly decode it as 0001011, and assume the original message was 0001.

Orthogonality Lemma. Let C be a systematic (n, k) linear code over F with a standard generator matrix G and parity-check matrix H. Then, ∀v ∈ Fⁿ, v ∈ C ↭ vH = 0.

Proof.

G = $\left( \begin{smallmatrix}1 & 0 & ··· & 0 | & a_{11} & ··· & a_{1n-k}\\ 0 & 1 & ··· & 0 | & a_{21} & ··· & a_{2n-k}\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\· & · & ··· & · | & · & · & ·\\ 0 & 0 & ··· & 1 | & a_{k1} & ··· & a_{kn-k}\end{smallmatrix} \right)$ = [I_k | A], I_k is the identity matrix k x k, H = [$\begin{smallmatrix}-A\\ I{n-k}\end{smallmatrix}$] has rank n - k, so we may think that H is a linear transformation from Fⁿ onto F^n-k ⇒ [Theorem Dimension Formula. Let L: V → W be a linear transformation with V a finite-dimensional vector space, then dim(V) = dim(ker(L)) + dim(Img(L)) = dim(Ker(L)) + rank(L)] n = dim(Ker(H)) + (n-k) ⇒ dim(Ker(H)) = k.

GH = [I_k | A] [$\begin{smallmatrix}-A\\ I{n-k}\end{smallmatrix}$] = -A + A = [0] 🚀

By construction, ∀v ∈ C, v = mG where m is a message vector ⇒ vH = (mG)H = m(GH) =[🚀] m[0] = 0 ⇒∀v ∈ C, v ∈ Ker(H) ⇒ C ⊆ Ker(H) ⇒ [dim(Ker(H)) = k = dim(C)] C = Ker(H), that is, v ∈ C ↭ vH = 0∎

Theorem. Parity-check matrix decoding will correct any single error iff if the rows of the parity-check matrix are nonzero and no one row is a scalar multiple of any other.

Proof (only the binary case)

Let H be the parity-check matrix, suppose that the rows are non-zero and distinct (we are going to demonstrate only the binary case), and the transmitted code word v was received with only one error in the ith position, say w.

Let e_i be the vector that has a 1 in ith position and 0s elsewhere (0 ··· 1_{ith position or place} ··· 0), so we may rewrite the received word as w = v + e_i (for simplicity’s sake, we are working only in the binary case) ⇒ [By the previous lemma, ∀v ∈ Fⁿ, v ∈ C ↭ vH = 0, therefore vH = 0] wH = (v + e_i)H = vH + e_iH = 0 + e_iH = e_iH, and this is precisely the ith row of H. Thus, if there is exactly one error in transmission, we can use the rows of the parity-check matrix not only to identify, but to correct the location of the error, provided that these rows are distinct. Of course, if two rows are the same, say the ith and jth rows, then we can tell that an error has indeed occurred, but we do not know in which row, that is, we cannot correct it.

Conversely, let’s suppose that the parity-check matrix method correctly decodes and corrects words in which at most one error has occurred. For the sake of contradiction, let’s suppose the ith row of the parity-check matrix H was the zero vector. If the codeword v = 0···0 is sent, and an error changes the ith bit, resulting in the message e_i being transmitted, the receiver could not detect the error because wH = (v + e_i)H = vH + e_iH = 0 + e_iH = e_iH = 0···0 = ith row of H, and erroneously concludes that the message e_i was sent ⊥

Let’s suppose that the ith and jth rows of H are equal, i ≠ j. When the codeword 00··· 0 is sent, and an error changes the ith bit, resulting in the message e_i being received, wH = (v + e_i)H = vH + e_iH = 0 + e_iH = e_iH= 0···0 = ith row of H = jth row of H ⇒ our decoding algorithm tell us not to decode ⊥ (By assumption, the parity-check matrix method correctly decodes and corrects words in which at most one error has occurred).

Coset Decoding

Let’s consider the fact that an (n, k) linear code C over a finite field F is a subgroup of the additive group of V = Fⁿ.

Consider the (6,3) binary linear code C = {000000, 100110, 010101, 001011, 110011, 101101, 011110, 111000}.

We are going to create a table, the standard array, as follows,

• The first row is the set C of code words. In other words, it starts with the zero codeword first.

  Coset Leader			Words
  000000	100110	010101	001001	110011	101101	011110	111000

• Each new row (rth) is a new coset of C, that is, to form a new row choose an element v ∈ V not listed in the table thus far, e.g., 100000. Among all elements of the coset v + C, let’s pick one of minimum weight, the coset leader or representative, say v’, which is not already included in the first r-1 rows, e.g., 100000 has minimum weight among the elements of the coset v + C, that is, 100000 + C = {100000, 000110, 110101, 101011, 0110011, 001101, 111110, 011000}.

  Coset Leader			Words
  000000	100110	010101	001011	110011	101101	011110	111000
  100000	000110	110101	101011	010011	001101	111110	011000

• Continue the algorithm until all the vectors in V are included in the table.

  Coset Leader			Words
  000000	100110	010101	001011	110011	101101	011110	111000
  100000	000110	110101	101011	010011	001101	111110	011000
  010000	110110	000101	011001	100011	111101	001110	101000
  001000	101110	011101	000011	111011	100101	010110	110000
  000100	100010	010001	001111	110111	101001	011010	111100
  000010	100100	010111	001001	110001	101111	011100	111010
  000001	100111	010100	001010	110010	101100	011111	111001
  100001	000111	110100	101010	010010	001100	111111	011001

The decoding algorithm is quite simple. One can decode a received word as the code word (first row) in the vertical column containing the received word, e.g., 101001, 101100, and 001100 are decoded as 101101; 011000, 101000, and 011001 are decoded as 111000.

Theorem. The coset decoding is the same algorithm as nearest-neighbor decoding.

Proof.

Let C be a linear code (i.e., our coset), w be a received word. If v is the coset leader of the coset containing w, then w + C = v + C ⇒ ∃c ∈ C: w = v + c, and w is decoded as c.

Let c’ be any arbitrary code word (c’∈ C) ⇒ w - c’ ∈ w + C = v + C ⇒ [By assumption, the coset leader v was chosen as a vector of minimum weight among the members of v + C] wt(w - c’) ≥ wt(v) ⇒ d(w, c’) = wt(w - c’) ≥ wt(v) = wt(w -c) = d(w, c). Therefore, w is decoded as the code word c which has minimum distance to w among all code words.

Definition. Let C be an (n, k) linear code over F with a parity-check matrix H. Given any vector u ∈ Fⁿ, the vector uH is called the syndrome of u.

Theorem. Let C be an (n, k) linear code over F with a parity-check matrix H. Then, two vectors of Fⁿ are in the same coset of C if and only if they have the same syndrome.

Proof:

Let u, v ∈ Fⁿ are in the same coset of C ↭ u - v ∈ C ⇒ [By the Orthogonality Lemma ∀v ∈ Fⁿ, v ∈ C ↭ vH = 0.] u and v are in the same coset ↭ 0 = (u -v)H = uH -vH ↭ uH = vH, that is, they both have the same syndrome.

Syndrome decoding for a received word w:

1. Compute wH, the syndrome.
2. Find the coset leader v such that wH = vH.
3. Decode the vector as w -v (wH = vH ↭ w -v∈ H, both the coset and our code).
   We are using C ≤ Fⁿ, a subgroup of the additive group of V = Fⁿ, we could use additive notation w+H = v+H ↭ w -v∈ H

Example.

$H = \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right).$

$\left( \begin{smallmatrix}1\\ 0\\ 0\\ 0 \\ 0\\ 0\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 1\\ 0\end{smallmatrix} \right)$

To decode w = 101001,

$wH=\left( \begin{smallmatrix}1\\ 0\\ 1\\ 0 \\ 0\\ 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 0\\ 0\end{smallmatrix} \right) = \left( \begin{smallmatrix}0\\ 0\\ 0\\ 1 \\ 0\\ 0\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) $ ⇒ w - v (coset leader) = (101001) - (000100) = 101101 was the original message sent.

To decode w = 011001,

$wH=\left( \begin{smallmatrix}0\\ 1\\ 1\\ 0 \\ 0\\ 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 1\\ 1\end{smallmatrix} \right) = \left( \begin{smallmatrix}1\\ 0\\ 0\\ 0 \\ 0\\ 1\end{smallmatrix} \right) \left( \begin{smallmatrix}1 & 1 & 0\\1 & 0 & 1\\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{smallmatrix} \right) $ ⇒ w - v (coset leader) = (011001) - (100001) = 111000 was the original message sent.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.