Automorphisms

They came up through long discussions, painstaking research, in-depth analysis, some tragic murderers and mysterious disappearances, and trial and error experimentation with abducted human beings involving their genitalia with the Ten Immutable, Absolute, and Transcendent Laws of Physics, Psychology, Philosophy, and Reality that I will so kindly share with you and show you below [···]

Males are fucked when getting married, no matter what species. The game is rigged. [···] There is a special place in hell for people who don’t flush the toilet. [···] Males can love females, but not understand them and have delusions of adequacy and conceit. On the other hand, females are crazy. The reason why females are crazy is because their male partners make them want to chew their veins violently and without mercy. [···] Most properties apply to the empty set, some less properties apply to finite sets, Apocalypse, Anawim, #justothepoint.

Recall

Let (A, *) and (B, ⋄) be two binary algebraic structures. A homomorphism is a structure-preserving map between two algebraic structures of the same type (groups, rings, fields, vector spaces, etc.) or, in other words, a map ϕ: A → B, such that ∀x, y ∈ S : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y).

Notice that ϕ may not be one to one (injection), nor onto (surjection). An isomorphism is a bijective homomorphism, i.e., one-to-one and onto. In other words, let (S, *) and (S’, ⋄) be two binary algebraic structures of the same type. An isomorphism of S with S' is a 1-1 function ϕ mapping from S onto S′ such that the homomorphism property holds: ∀x, y ∈ S : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y). S and S’ are said to be isomorphic binary structures and we denote or write it by S ≋ S'.

In particular, two groups (G, *) and (G', ⋄) are isomorphic if there exist a bijective homomorphism, i.e., a one-to-one and onto map Φ: G → G’ such that the group operation is preserved, that is, ∀x, y ∈ G : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y). Isomorphic groups are equivalent, that is, they share the same algebraic and group theoretic properties.

Definition. An automorphism is an isomorphism from a group to itself.

Examples:

1. There are two automorphism of ℤ: the identity, and the mapping n → -n.
2. The conjugation map, i.e., Φ: ℂ → ℂ, Φ(a + bi) = a - bi is an automorphism of (ℂ, +).
3. Let ℝ² = {(a, b) | a, b ∈ ℝ}, Φ: ℝ² → ℝ², Φ(a, b) = Φ(b, a), the reflection across the vertical line y = x, is an automorphism of (ℝ², +).
4. f: ℝ → ℝ, ∀x ∈ ℝ, f(x) = αx, f is a group automorphism ↭ α ≠ 0.
5. There is an automorphism Φ: ℤ₅ → ℤ₅, for each choice of Φ(1) ∈ {1, 2, 3, 4}. Notice that Φ(0) = 0 (Φ always carries the identity).

Definition. Let G be a group, and let a be a fixed or given element of G, a ∈ G.An inner automorphism of G (induced or given by a) is defined by the conjugation action of the fixed element a, called the conjugating element i.e., Φ_a defined by Φ_a(x) = a·x·a^-1 ∀x ∈ G.

Proof. Φ_a is an automorphism of G.

1. Φ_a is a group homomorphism, ∀x₁, x₂ ∈ G, Φ_a(x₁x₂) =[By definition] a·(x₁x₂)·a^-1 = a·(x₁·a^-1·a·x₂)·a^-1 =[Associativity] (ax₁a^-1)(ax₂a^-1) = Φ_a(x₁)Φ_a(x₂)
2. It has an inverse, namely Φ_a^-1. Thus, Φ_a is bijective, and so is an automorphism∎

We can also prove that is injective Φ_a(x₁) = Φ_a(x₂) ↭ a·x₁·a¹ = a·x₂·a^-1 ↭ [Cancellation laws] x₁ = x₂. Besides, ∀x∈ G, since G is closed a^-1·x·a ∈ G, then Φ_a(a^-1·x·a) = [By definition] a·(a^-1·x·a)·a^-1 = [Associativity] (a·a^-1)·x·(a·a^-1) = x ⇒ surjective∎

Example. Let’s compute the inner automorphism of D₄ induced by R_90°. It is shown in the following Figure 1.a.

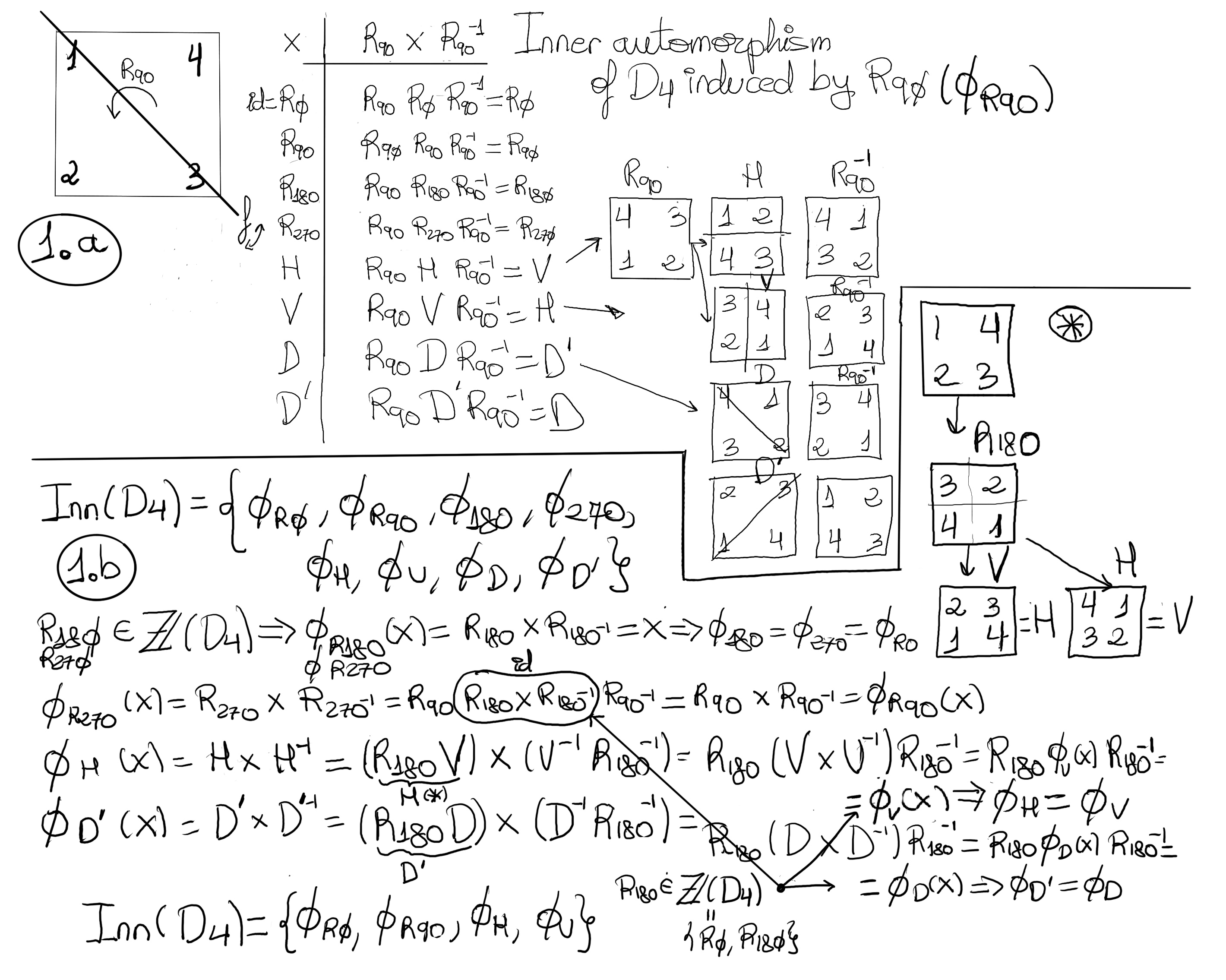
Definition. Let G be a group, we use Aut(G) and Inn(G) to express or denote the set of all automorphisms and inner automorphisms respectively. They are both groups under composition.

Aut(G) = {Φ: G → G’: Φ is an isomorphism}

Inn(G) = {Φ_g: G → G’: Φ(x) = g·x·g^-1}

Proof (Aut(G) forms a group).

1. Let be id: G → G, id(a) = a, ∀a ∈ G. Then, id∘Φ = Φ∘id = Φ, and therefore id ∈ Aut(G)
2. Associativity follows from the associativity of the compositions of functions.
3. ∀Φ ∈ Aut(G), Φ is an isomorphism ⇒ Φ has an inverse for composition of functions ∘, say Φ^-1. is Φ^-1 a group homomorphism? ∀a, b ∈ G, ∃a’, b’: Φ(a’) = a, Φ(b’) = b ⇒ Φ^-1(ab) = Φ^-1(Φ(a’)Φ(b’)) =[Φ is a group homomorphism] Φ^-1(Φ(a’b’)) = a’b’ = Φ^-1(a)Φ^-1(b). Φ is bijective ⇒ Φ^-1 is bijective ⇒ Φ^-1 ∈ Aut(G).
4. ∀Φ, Φ’ ∈ Aut(G), (Φ ∘ Φ’)(ab) = Φ(Φ’(ab)) = [In particular, Φ’ is a group homomorphism] Φ(Φ’(a)Φ’(b)) = [Φ is group homomorphism] Φ(Φ’(a))Φ(Φ’(b)) = (Φ ∘ Φ’)(a)(Φ ∘ Φ’)(b) ⇒ Φ ∘ Φ’ ∈ Aut(G)∎

Theorem. Let G be a group. Then, the set Inn(G) of all inner automorphisms forms a normal subgroup of the automorphism group, Inn(G) ◁ Aut(G).

Proof. (Let’s use the subgroup test, H ≤ G iff ∀ x, y ∈ H, xy^-1 ∈ H)

∀ Φ_a, Φ_b ∈ Inn(G). We claim (Φ_b)^-1 = Φ_b^-1

∀g ∈ G, (Φ_b∘Φ_b^-1)(g) = (Φ_b)((Φ_b^-1)(g)) = (Φ_b)(b^-1gb) = b(b^-1gb)b^-1 =[Associativity] (bb^-1)g(bb^-1) = g.

∀g ∈ G, (Φ_b^-1∘Φ_b)(g) = (Φ_b^-1)((Φ_b)(g)) = (Φ_b^-1)(bgb^-1) = b^-1(bgb^-1)b =[Associativity] (b^-1b)g(b^-1b) = g. Therefore, ∀g ∈ G, (Φ_b∘Φ_b^-1)(g) = (Φ_b^-1∘Φ_b)(g) = g ⇒ (Φ_b)^-1 = Φ_b^-1

∀ Φ_a, Φ_b ∈ Inn(G), ∀g ∈ G, Φ_a∘(Φ_b)^-1(g) = Φ_a∘Φ_b^-1(g) = Φ_a(Φ_b^-1(g)) = a(b^-1gb)a^-1 =[Associativity] (ab^-1)g(ba^-1) =[The Socks and Shoes Principle] (ab^-1)g(ab^-1)^-1 = Φ_ab^-1(g) ⇒ Φ_a∘(Φ_b)^-1 ∈ Inn(G) ⇒ Inn(G) ≤ Aut(G)

∀Φ ∈ Aut(G), ∀Φ_a ∈ Inn(G), Φ∘Φ_a∘Φ^-1 ∈ Inn(G)? Claim: Φ∘Φ_a∘Φ^-1 = Φ_Φ(a)

∀g ∈ G, (Φ∘Φ_a∘Φ^-1)(g) = (Φ∘Φ_a)(Φ^-1(g)) = Φ(Φ_a(Φ^-1(g))) = Φ(a·Φ^-1(g)·a^-1) =[In particular, Φ is a group homomorphism] Φ(a)·Φ(Φ^-1(g))·Φ(a^-1) =[∀n ∈ ℤ, ∀a ∈ G, Φ(aⁿ) = (Φ(a))ⁿ] Φ(a)·g·Φ(a)^-1 = Φ_Φ(a)(g) ⇒ ∀Φ ∈ Aut(G), ∀Φ_a ∈ Inn(G), Φ∘Φ_a∘Φ^-1 = Φ_Φ(a) ∈ Inn(G) ⇒ Inn(G) ◁ Aut(G) ∎

Example. Let’s compute Inn(D₄). Observe that the complete list of inner automorphism is {Φ_R0, Φ_R90, Φ_R180, Φ_R270, Φ_H, Φ_V, Φ_D, Φ_D’} where R₀, R₉₀, R₁₈₀ and R₂₇₀ are rotations of a square, H and V denote the horizontal reflections, and D and D’ denote the diagonal reflections. This list may have repeated automorphisms.

Recall, ℤ(D_n) = $ \begin{cases} e, n~is~ odd\\\\ e~ and~ α^{\frac{n}{2}}, n~is~ even \end{cases}$

Therefore, ℤ(D₄) = {e, α²} = {R₀, R₁₈₀} ⇒ Φ_R180(x) = R₁₈₀xR₁₈₀^-1 [R₁₈₀ ∈ ℤ(D₄) ↭ R₁₈₀x = xR₁₈₀] = x ⇒ Φ_R180 = Φ_R0.

Φ_R270(x) = R₂₇₀xR₂₇₀^-1 =[R₂₇₀ = R₉₀R₁₈₀] R₉₀R₁₈₀xR₁₈₀^-1R₉₀^-1 = R₉₀(R₁₈₀xR₁₈₀^-1)R₉₀^-1 = R₉₀xR₉₀^-1 ⇒ Φ_R270 = Φ_R90.

Inn(D₄) = [Figure 1.b, and considering H = R₁₈₀V, and D’ = R₁₈₀D] {Φ_R0, Φ_R90, Φ_H, Φ_D}.

Example. Let’s compute Aut(ℤ₁₀)

Let be α ∈ Aut(ℤ₁₀). Once we know α(1), we know α(k) for any k, because α(k) = α(1+··_k··+1) = α(1)+··_k··+α(1) = kα(1)

We have already demonstrated that ∀Φ isomorphism from G to G’, |a| = |Φ(a)| ∀a in G, i.e., isomorphisms preserve order and also map generators to generators -Properties of Isomorphisms acting on elements- ⇒ |α(1)| = |1| = 10 ⇒ There are four candidates for α(1) -4 generators of ℤ₁₀, numbers less than 10 and coprime with 10-, namely α(1)=1 (let’s name this isomorphism as α₁), α(1)=3 (α₃), α(1)=7 (α₇), and α(1)=9 (α₉).

A similar argument will reveal that the possible automorphisms of ℤ₈ are α(1) = 1 (id), α(1) = 3 (α₃), α(1) = 5 (α₅), and α(1) = 7 (α₇).

α₁ is the identity. is α₃ an automorphism?

α₃(1)=3, α₃(k) = kα₃(1) = 3k mod 10.

1. Is it well defined? [x]_ℤ10 = [y]_ℤ10 ⇒ x mod 10 = y mod 10 ⇒ 3x mod 10 = 3y mod 10.
2. Is α₃ onto? Yes, it is, because α(1) = 3 and 3 is a generator of ℤ₁₀.
3. Is α₃ one to one? 3a mod 10 = 3b mod 10 ⇒ (3a-3b) mod 10 = 0 mod 10 ⇒ a-b mod 10 = 0 mod 10 ⇒ [a]_ℤ10 = [b]_ℤ10
4. Is it a homomorphism? α₃(a + b) = 3(a + b) = 3a + 3b = α₃(a)α₃(b)

Therefore α₃ is an automorphism. The same argument shows that α₇ and α₉ are automorphisms, too. Aut(ℤ₁₀) = {α₁, α₃, α₇, α₉}

What is it structure? (α₃α₃)(1) = α₃(α₃(1)) = α₃(3) = 3·3 = 9 = α₉(1) ⇒ α₃α₃ = α₉. Further calculations show that α₃³ = α₇ and α₃⁴ = α₁. Thus, Aut(ℤ₁₀) is cyclic, Aut(ℤ₁₀) = ⟨α₃⟩. Actually, it is isomorphic to U₁₀ = {1, 3, 7, 9}.

Theorem. ∀n ∈ ℤ, n > 0, Aut(ℤ_n)≋ U_n or ℤ_n^x, the group of the integers relatively prime to n under multiplication mod n. In particular, |Aut(ℤ_n)| = Φ(n) where Φ(n) is Euler’s totient function, which gives the number of positive integers less than or equal to n that are relatively prime to n.

Proof.

Let α ∈ Aut(ℤ_n). α(0) = 0. Once we know α(1), we know α(k) for any k∈ℤ_n because α(k) = α(1+1+··_k··+1) = α(1)+α(1)+··_k··+α(1) = kα(1). Any automorphism α is determined by α(1). Besides, α(1) ∈ U_n because it needs to be a generator of ℤ_n, that is, an integer less than n and coprime to n, but these integers are precisely the elements of U_n.

We claim that Φ: Aut(ℤ_n) → U_n, defined by Φ(α) = α(1) is an isomorphism.

1. is Φ one-to-one? Let α, β ∈ Aut(ℤ_n), and suppose Φ(α) = Φ(β) ⇒ α(1) = β(1) ⇒ α(k) = kα(1) = kβ(1) = β(k), ∀k ∈ ℤ_n ⇒ α = β
2. is Φ onto? Let r ∈ U_n, consider α: ℤ_n → ℤ_n defined as α(s) = sr (mod n), ∀s ∈ ℤ_n. It can easily be demonstrated that α ∈ Aut(ℤ_n), and Φ(α) = α(1) = r.
3. is Φ operation-preserving? ∀α, β ∈ Aut(ℤ_n), Φ(αβ) = (αβ)(1) = α(β(1)) = α(1+1+··_β(1)··+1) =[In particular, α is a group homomorphism] α(1)+α(1)+··_β(1)··+α(1) = α(1)β(1) = Φ(α)Φ(β) ∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.