Areas between curves

He may look like an idiot and talk like an idiot but don’t let that fool you. He really is an idiot, Groucho Marx.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Areas between curves

We want to determine the area between y = f(x) and y = g(x) on the interval [a, b]. For simplicity sake, we are also going to assume that f(x) ≥ g(x).

We could draw “small” rectangles whose areas are dx·(f(x)-g(x)) (Area = base·height). The total area on the interval [a, b] is the definite integral $\int_{a}^{b} (f(x)-g(x))dx$ -Figure 1.d.-.

In general, the area between two curves representing two arbitrary functions, say f and g, can be found by taking the definite integral of the absolute difference between the two functions over the interval of interest.  

How to calculate the area between two curves

• Find the area of the region enclosed by the curves and lines y = x² +1, y = x, x = 0, x = 1 (Figure 4).

1. Identify the region bounded by the given curves. Determine the points of intersection, if any, as they will define the limits of integration, e.g., $x^2+1 = x ↭ x^2-x+1=0 ↭ x = \frac{1±\sqrt{1-4}}{2}=\frac{1±\sqrt{-3}}{2}$. Since the discriminant is negative, the solutions are complex, which means the curves do not intersect in the real plane. The interval of interest is from x = 0 and x = 1, therefore a = 0 and b = 1.
2. Identify which function lies above the other in each segment of the given interval, e.g., in this case, y = x² + 1 lies above y = x.
3. Calculate the integral over the interval [a, b]. The integrand will be the absolute difference between the functions f(x) and g(x), Area = $\int_{a}^{b} |f(x)-g(x)|dx = \int_{0}^{1} x^2+1-xdx = \frac{x^3}{3}-\frac{x^2}{2}+x\bigg|_{0}^{1} = \frac{1}{3}+\frac{-1}{2}+1 = \frac{2}{6}+\frac{-3}{6}+\frac{6}{6} = \frac{5}{6}.$

Solved exercises

• Find the area between y = x² -4x and y = 2x (Figure 5).

First, we need to calculate the points of intersection of the two curves. $2x = x^2 -4x ⇒ x^2 -6x = 0 ⇒ x(x-6)=0 ⇒ x = 0, 6$. These are the points of intersection.

For x ∈ [0, 6], the upper function is y = 2x, and the lower function is y = x² - 4x.

The integral to find the area is $\int_{0}^{6} 2x-(x^2-4x)dx = \int_{0}^{6} (-x^2+6x)dx = \frac{-x^3}{3}+\frac{6x^2}{2} = \frac{-x^3}{3}+3x^2\bigg|_{0}^{6} = \frac{(-6)^3}{3}+3·6^2 = 36$.

• Calculate the blue-shaded area (Figure B).

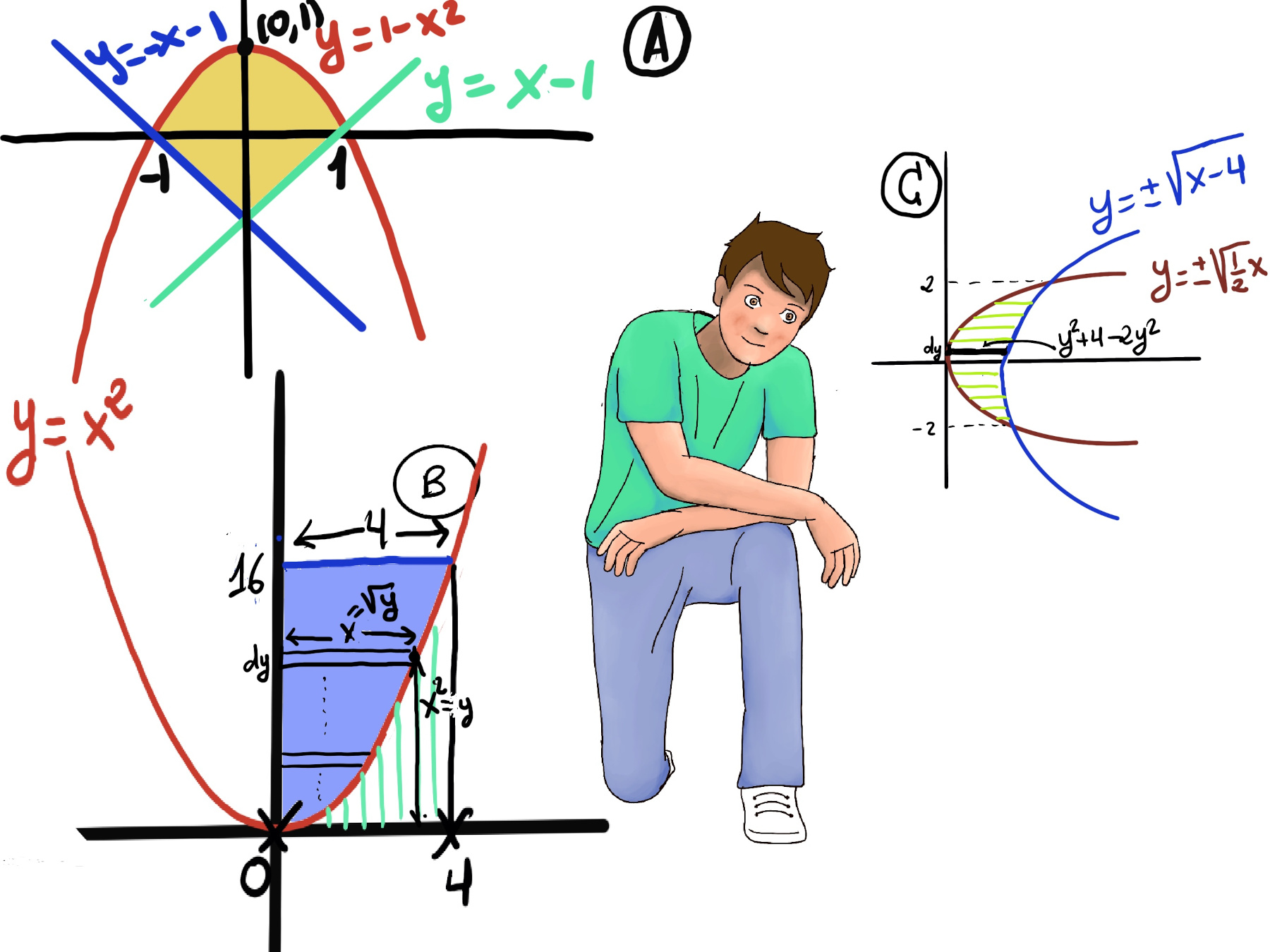
The easiest method is by subtraction. Area = $4*16-\int_{0}^{4} x^2dx = 64 -\frac{x^3}{3}\bigg|_{0}^{4} = 64 -\frac{4^3}{3} = \frac{128}{3}units^2$

We can also use horizontal slices with “small” heights dy and widths $\sqrt{y}$ from (0, 0) to (16, 4). Area = $\int_{0}^{16} \sqrt{y}dy = \frac{y^{\frac{3}{2}}}{\frac{3}{2}} = \frac{2}{3}y^{\frac{3}{2}}\bigg|_{0}^{16} = \frac{2}{3}16^{\frac{3}{2}} = \frac{2}{3}(16^{\frac{1}{2}})^3 = \frac{2}{3}(4^3) = \frac{64·2}{3} = \frac{128}{3}~units^2.$

• Calculate the green-shaded area (Figure C)

$y = ± \sqrt{\frac{1}{2}x} ↭ y^2 = \frac{1}{2}x ↭ x = 2y^2.~ y = ± \sqrt{x -4} ↭y^2 = x -4 ↭ x = y^2+4$

We are going to integrate with respect to y or, in other words, we will use horizontal slices with “small” heights dy and widths $y^2+4-2y^2$ from -2 to 2.

Area = $\int_{-2}^{2} (y^2+4-2y^2)dy = \int_{-2}^{2} (-y^2+4)dy = \frac{-y^3}{3}+4y\bigg|_{-2}^{2} = \frac{-8}{3}+8-(\frac{8}{3}-8) = \frac{-16}{3}+16 = \frac{-16}{3}+\frac{48}{3} = \frac{32}{3}~units^2.$

• Find the area between x = y² and y = x -2.

Calculate the points of intersection, in our particular case where x = y² and y = x -2 intersect. y = x -2 ⇒ x = y +2 =[x = y²] y² ↭ y + 2 = y² ↭ y² -y -2 = 0, (y -2)(y +1) = 0, y = 2 (4, 2) or y = -1 (1, -1).

Area =[Figure 1.e. Using vertical slices] $\int_{0}^{1} (\sqrt{x}-(-\sqrt{x}))dx$ (Left section, green area) + $\int_{1}^{4} (\sqrt{x}-(x-2))dx$ (Right section, red area) = $\int_{0}^{1} 2\sqrt{x}dx + \int_{1}^{4} (\sqrt{x}-(x-2)) = \int_{0}^{1} 2\sqrt{x}dx + \int_{1}^{4} (\sqrt{x}-x+2) = \left[ \frac{4}{3}x^{\frac{3}{2}} \right]_{0}^{1} +$

$\left[ \frac{2}{3}x^{\frac{3}{2}} - \frac{1}{2}x^2 + 2x \right]_{1}^{4} = \frac{4}{3}(1)^{\frac{3}{2}} - \frac{2}{3}(0)^{\frac{3}{2}} + \frac{2}{3}(4)^{\frac{3}{2}} - \frac{1}{2}(4)^2 + 2(4) - \frac{2}{3}(1)^{\frac{3}{2}} + \frac{1}{2}(1)^2 - 2(1)= \frac{4}{3}+\frac{2}{3}8 + -8 + 8 -\frac{2}{3}+\frac{1}{2}-2 = \frac{2}{3} +\frac{2}{3}8 + +\frac{1}{2}-2 = \frac{4+32+3-12}{6} = \frac{27}{6} = \frac{9}{2}$

Area =[Using horizontal slices with “small” heights dy and widths (y+2) -y² from (1, -1) to (4, 2), Figure 1.f] $\int_{-1}^{2} (y+2-y^2)dy = (\frac{y^2}{2}+2y-\frac{y^3}{3})\bigg|_{2}^{-1} = \frac{1}{2}(2)^2 + 2(2) - \frac{1}{3}(2)^3 -(\frac{1}{2}(-1)^2 + 2(-1) - \frac{1}{3}(-1)^3)= \frac{10}{3}+\frac{7}{6} = \frac{20}{6}+\frac{7}{6} = \frac{27}{6} = \frac{9}{2}.$

• Compute the area between f(x) = -x² + 4x and g(x) = x²-6x+5 over the interval [0, 1] (Figure 3)

1. Calculate the points of intersection of the two curves $-x^2+4x = x^2-6x+5 ↭ 2x^2-10x +5 = 0↭ x = \frac{10±\sqrt{100-40}}{4}= \frac{5±\sqrt{15}}{2}, x = \frac{5-\sqrt{15}}{2} ∈ [0, 1]$. For the sake of brevity, i = $\frac{5-\sqrt{15}}{2}$.

2. Determine the intervals of interest: $[0, \frac{5-\sqrt{15}}{2}], [\frac{5-\sqrt{15}}{2}, 1]$

3. Take the absolute difference between the two functions and integrate over each interval separately to find the area.

$\int_{0}^{i} x^2-6x+5 -(-x^2+4x)dx + \int_{i}^{1} -x^2+4x - (x^2-6x+5)dx = \int_{0}^{i} (2x^2-10x+5)dx + \int_{i}^{1} (-2x^2+10x-5)dx = \frac{2x^3}{3}-\frac{10x^2}{2}+5x\bigg|_{0}^{i}$ +

$-\frac{2x^3}{3}+\frac{10x^2}{2}-5x\bigg|_{i}^{1} = $… = $\frac{-52}{3}+5\sqrt{15}$

• Calculate the area of the shaded region bounded by three curves, y = -x-1, y = 1 -x², y = x -1 (Figure A)

To calculate the area of the shaded region bounded by the curves y = -x-1, y = 1 -x², y = x -1, we need to find the points of intersection. For y = -x-1, y = 1 -x², -x -1 = 1 -x² ↭ x²-x -2 = 0 ↭ (x-2)(x+1) = 0 ↭ x = 2, -1. For y = 1 -x² and y = x -1, 1 -x² = x -1 ↭ x² + x -2 = 0 ↭ (x+2)(x-1) = 0 ↭ x = -2, x = 1.

The shaded region is composed of two segments: The segment between y = 1 - x² and y = x −1 from x = -1 to x = 0. The segment between 1 - x² and y = x - 1 from x = 0 to x = 1.

$\int_{-1}^{0} ((1-x^2)-(-x-1))dx + \int_{0}^{1} ((1-x^2)-(x-1))dx =$[Because the graph is symmetric respect to the y-axix] $2\int_{0}^{1} (-x^2-x+2)dx = 2(\frac{-x^3}{3}-\frac{x^2}{2}+2x)\bigg|_{0}^{1} = 2(\frac{-1}{3} -\frac{1}{2}+2)= 2(\frac{-2}{6}-\frac{3}{6}+\frac{12}{6}) = 2·\frac{7}{6} = \frac{7}{3}.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.