Groups III. Symmetries. Group Actions.

To raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advance in science, Albert Einstein.

Proposition. Suppose G is a group. If ∀a, b ∈ G (ab)² = a²b², then ab = ba.

Proof.

a(ab)b = a²b² = [By assumption] (ab)² = (ab)(ab) = [Associative] a(ba)b

a(ab)b = a(ba)b ⇒ [Cancellation laws ↭ multiplying both sides by a^-1, and then, by b^-1] ab = ba∎

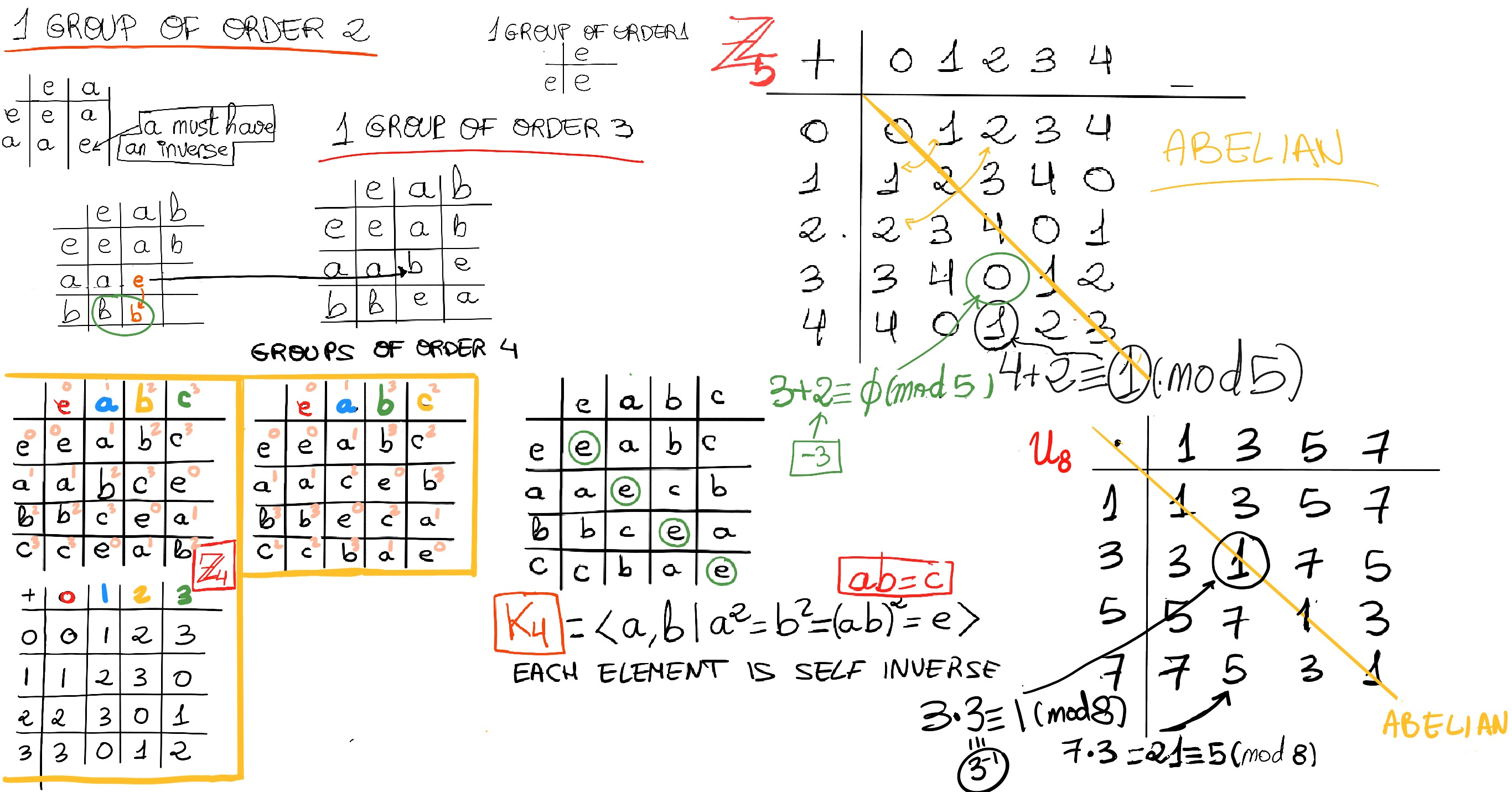
Proposition. If every non-identity element of G has order 2, then G is Abelian.

Proof.

G is Abelian ↭ ∀a, b ∈ G, ab = ba.

∀a, b ∈ G ⇒ [G group, it is closed under the group operation] ab ∈ G ⇒ [∀a ∈ G, a² = e, notice that e²= e, too] (ab)² = e ⇒ ab = (ab)^-1 = [Shoes and socks principle] b^-1a^-1 = [Every element is its own inverse] ba∎

Cayley Tables

A Cayley table describes the structure of a finite group by arranging all the possible products of all the group’s elements in a square table.

Let G = {a₁, a₂, ···, a_n}. The group operation (e.g., +, x, *, ·, ∘) is placed in the upper left corner of the table. Next, we place the elements of the set in the head row and the head column. The i, j entry, that is, the intersection of row i and column j corresponds to the group element a_i · a_j. For example, let’s say the group G ({1, -1, i, -i}, x), -1·-1 = 1, -1·i = -i, -1·-i = i, etc.

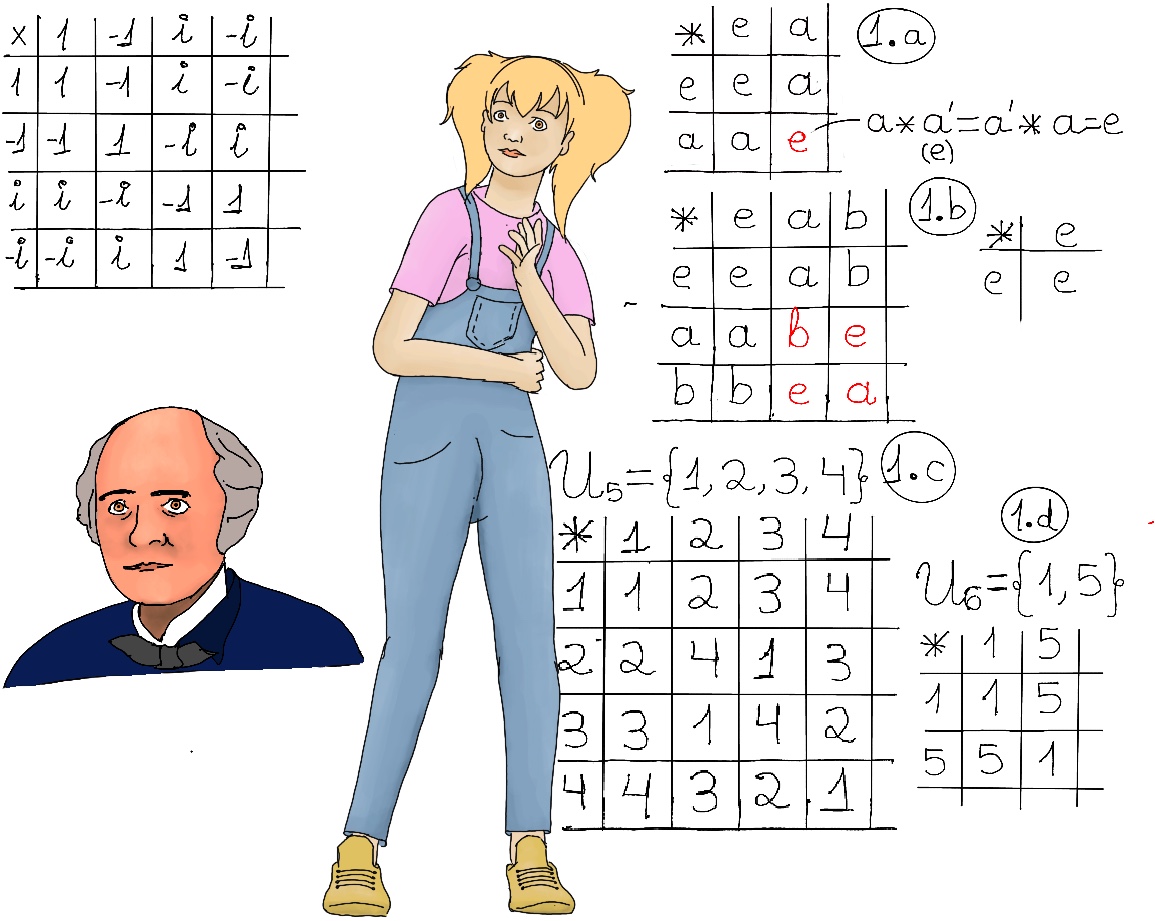
Let’s take into consideration the Cayley table for G ({1, -1, i, -i}, x).

1. The first row and first column are trivial; since e does nothing, the first row matches the head row, and the first column matches the head column.
2. Every row and every column contains the identity element (1) because every element in a group has an inverse.
3. There is no duplicate elements in any row or column. Let’s suppose there’s a row with duplicate elements a∘x = a∘y, x ≠ y ⇒ a^-1∘(a∘x) = a^-1∘(a∘y) ⇒ (a^-1∘a)∘x = (a^-1∘a)∘y ⇒ x = y ⊥.
4. A binary operation is commutative if and only if the entries in the table are symmetric with respect to the principal diagonal that starts at the upper left corner of the table (1 x 1 = 1) and ends at the lower right corner (-i x -i = -1).

Finite Groups

1. |G| = 0 ⊥ It is simply not possible, a minimal set that might give rise to a group needs to contain, at the very least, the identity by definition.
2. |G| = 1. It is easily defined by e∘e = e. This “small” group is called the trivial group (Figure 1.b).
3. |G| = 2. Observe that every row and column must contain all the group elements (no duplicates), and therefore a ∘ a = e. Besides, a must have an inverse. There’s only one group of order 2, and this group is isomorphic to ℤ₂ = {0, 1} under addition modulo 2. Both Cayley’s tables are structurally the same, just replace e by 0, and a by 1, (Figure 1.a).
4. |G| = 3. Let the set be {e, a, b}. It can be easily demonstrated that the table must be filled in as shown in 1.b. if each row and column are to contain each element exactly once (Figure 1.b. Observe that a·a = b and the rest follows immediately).
5. There are exactly 2 groups of order 4, up to isomorphism: ℤ₄, the cyclic group of order 4 and K₄, the Klein 4-group.

Symmetries

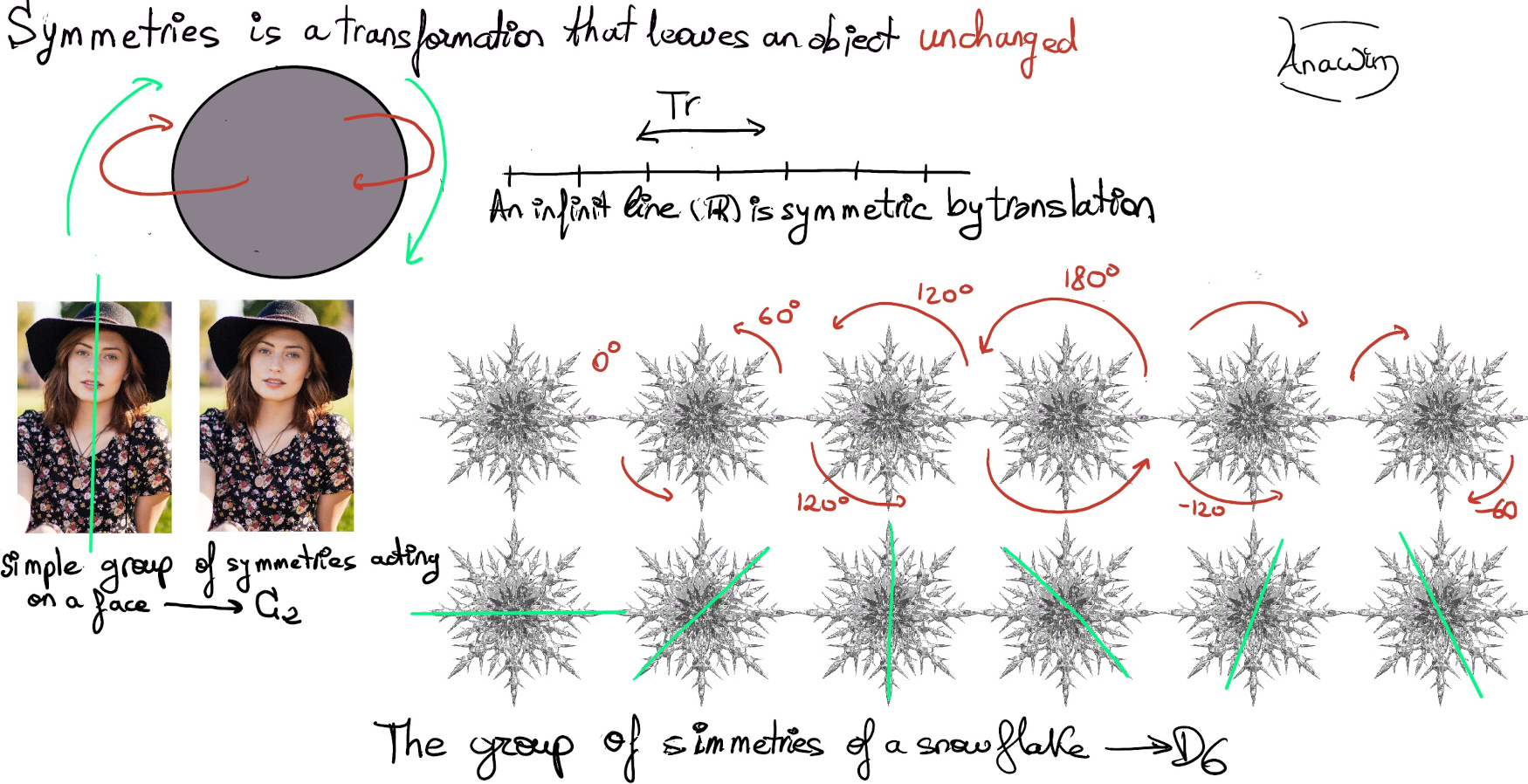
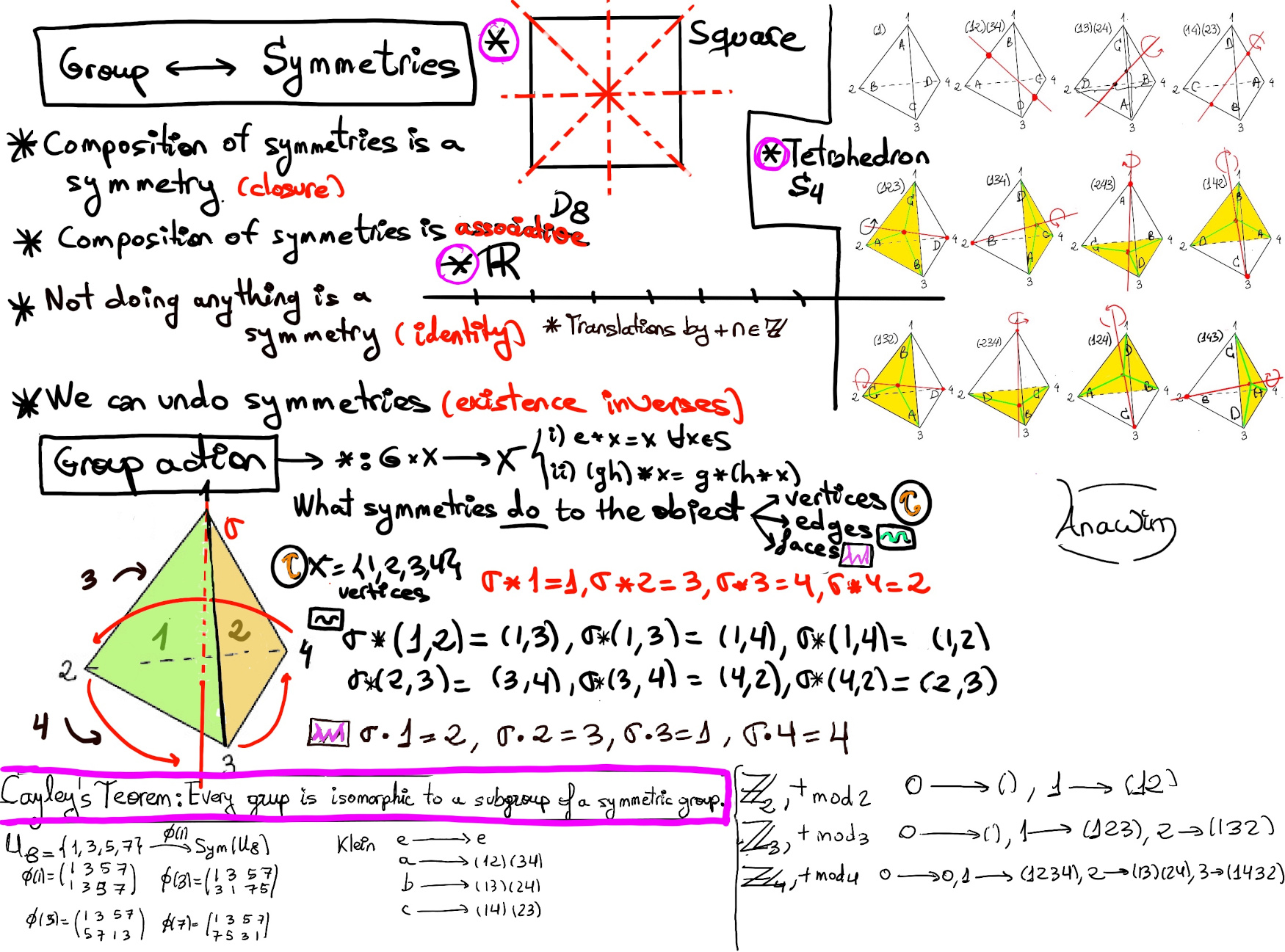
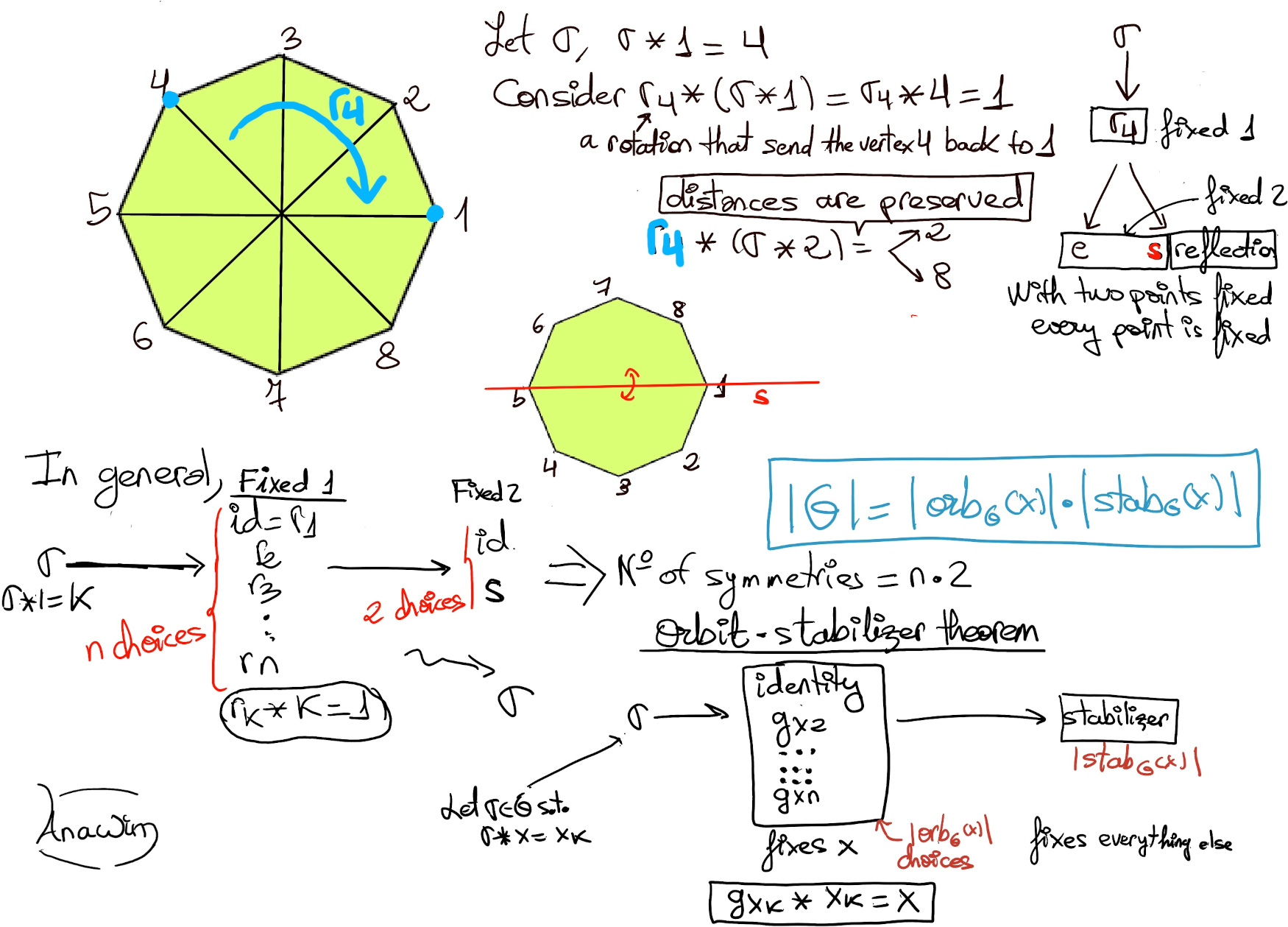
Indeed group theory is the mathematical language of symmetry. We can think groups as symmetries (a transformation that preserves both distances and the object itself). Futhermore, symmetries of an object (a plane figure -square-, a solid figure -tetrahedron- or a real number line ℝ) do form a group (💡Source: Mathemaniac YouTube’s channel, Essence of Group Theory).

1. X = {1, 2, 3} vertices, σ: G x X → X, σ rotation with respect to the 1 vertex (rotations acting on vertices), σ * 1 = 1, σ * 2 = 3, σ * 3 = 4, σ * 4 = 2.
2. X = {(1, 2), (1, 3), (1, 4), (2, 3), (3, 4), (4, 2)} edges (rotations acting on edges), σ * (1, 2) = (1, 3), σ * (1, 3) = (1, 4), σ * (1, 4) = (1, 2), σ * (2, 3) = (3, 4), σ * (3, 4) = (4, 2), σ * (4, 2) = (2, 3)
3. X = {1, 2, 3} faces (rotations acting on faces), σ: G x X → X, σ * 1 = 2, σ * 2 = 3, σ * 3 = 1, σ * 4 = 4.

Group Actions

Definition. A group action of a group G on a set A, written as g·a or simply ga (g acts on a), is a map or function from G x A to A such that the following two conditions hold:

1. g₁·(g₂·a) = (g₁g₂)·a, ∀g₁, g₂ ∈ G, a ∈ A.
2. e·a = a, ∀a ∈ A.

Proposition. Let the group G act on a set A. For each fixed element of G, say g ∈ G, we get a permutation σ_g: A → A defined by σ_g(a) = g·a. Besides, the map from Φ: G → S_A defined by g → σ_g is a homomorphism. It is called the permutation representation associated to the given action.

Proof. We know that the map f: A → B is a bijection if and only if there exists g: B → A, the inverse of f, such that f∘g is the identity map on B and g∘f is the identity map on A.

∀g ∈ G, ∃g^-1, we claim that σ_g^-1 is the inverse of σ.

(σ_g^-1∘σ_g)(a) = [By definition of function composition] σ_g^-1(σ_g(a)) = σ_g^-1(g·a) = g^-1·(g·a) = [By property 1 of a group action] (g^-1g)·a = e·a = [By property 2 of a group action] a

Since g was chosen arbitrary, we may interchange the roles of g and g^-1 ⇒ σ_g is a permutation of A.

is the map Φ: G → S_A a homomorphism? We have already proved that σ_g ∈ S_A.

Φ(g₁g₂) = Φ(g₁)∘Φ(g₂)?

∀a ∈ A, Φ(g₁g₂)(a) = σ_g1g2(a) = (g₁g₂)·a = [By property 1 of an action] g₁·(g₂·a) = σ_g1(σ_g2(a)) = (Φ(g₁)∘Φ(g₂))(a)

Basically, a group action just means that every element g in G acts as a permutation on A in a way that is consistent with the group operation in G. Let Φ: G → S_A be any homomorphism from a group G to the symmetric group on a set, then the map from G x A to A defined by ∀g ∈ G, a ∈ A, g·a = Φ(g)(a) is a group action of G on A, and therefore actions on a group and homomorphisms from this group into the symmetric group S_A are basically the same construct or, more formally, in bijective correspondence.

Examples:

• Let G be a group, A a non empty set, the trivial action is defined as g·a = a ∀g ∈ G, a ∈ A. Observe that distinct elements of the group G induce the same permutation, that is, the identity permutation. The associated permutation representation Φ: G → S_A is the trivial homomorphism. It maps every element g ∈ G to the identity permutation.

Definition. If G acts on a set A and distinct elements of G induce distinct permutations of A, that is, when g₁ ≠ g₂ in G, there is an a ∈ A such that g₁·a ≠ g₂·a, the action is called faithful. The kernel of the action of G on A is {g ∈ G | ga = a ∀a ∈ A}

• The symmetric group (G =) S_A acting on A, S_A x A → A, by σ·a = σ(a) ∀σ ∈ S_A, a ∈ A. The associated permutation representation Φ: S_A → S_A is the identity map.

• We can make ℝⁿ act on itself by translations, for v ∈ ℝⁿ, let T_v: ℝⁿ → ℝⁿ, defined by T_v(w) = w + v. The axioms for a group action are: T₀(w) = w and T_v1(T_v2(w)) = T_v1+v2(w). These are true properties of vector addition: w + 0 = w, (w + v₂) + v₁ = w + (v₁ + v₂).

• For n ≥ 3, D_n acts on a regular n-gon as rigid motions. We can also view D_n as acting just on the n vertices of a regular n-gon. This does not lose any information at all, since knowing where each and every vertex go under a rigid motion determines completely where everything else goes. By focusing on the action of D_n on the n vertices, and labelling them by 1, 2, ···, n, we make D_n act on {1, 2, ···, n} (See the previous illustration).

• We can make G act on itself by left multiplication. We let A = G and g·a = ga is merely the usual product of g and a in G.

• Let G = ℤ/4ℤ act on itself by additions. For instance, addition by 1 has the effect 0 → 1 → 2 → 3 → 0. Addition by 1 on ℤ/4ℤ is a 4-cycle (0123). Addition by 2 has the effect 0 → 2 → 4, 1 → 3, it is a product of two 2-cycles, (02)(13). The composition of these two permutations is (0123)(02)(13) = (0321) which is the permutation of G described by addition by 3.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.