Limits of Rational Functions

Men lie, women lie, numbers don’t, Lil B

Recall

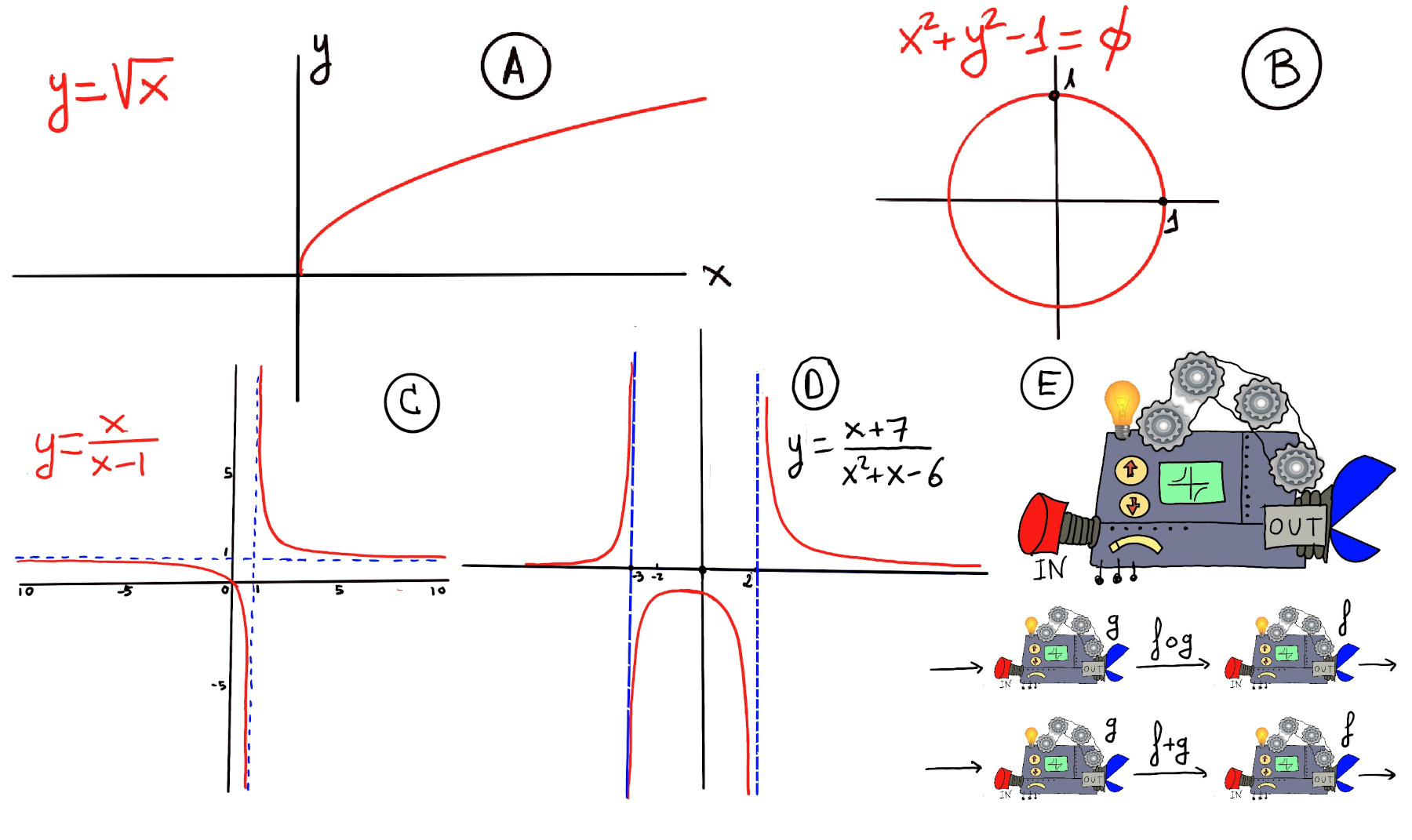
Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

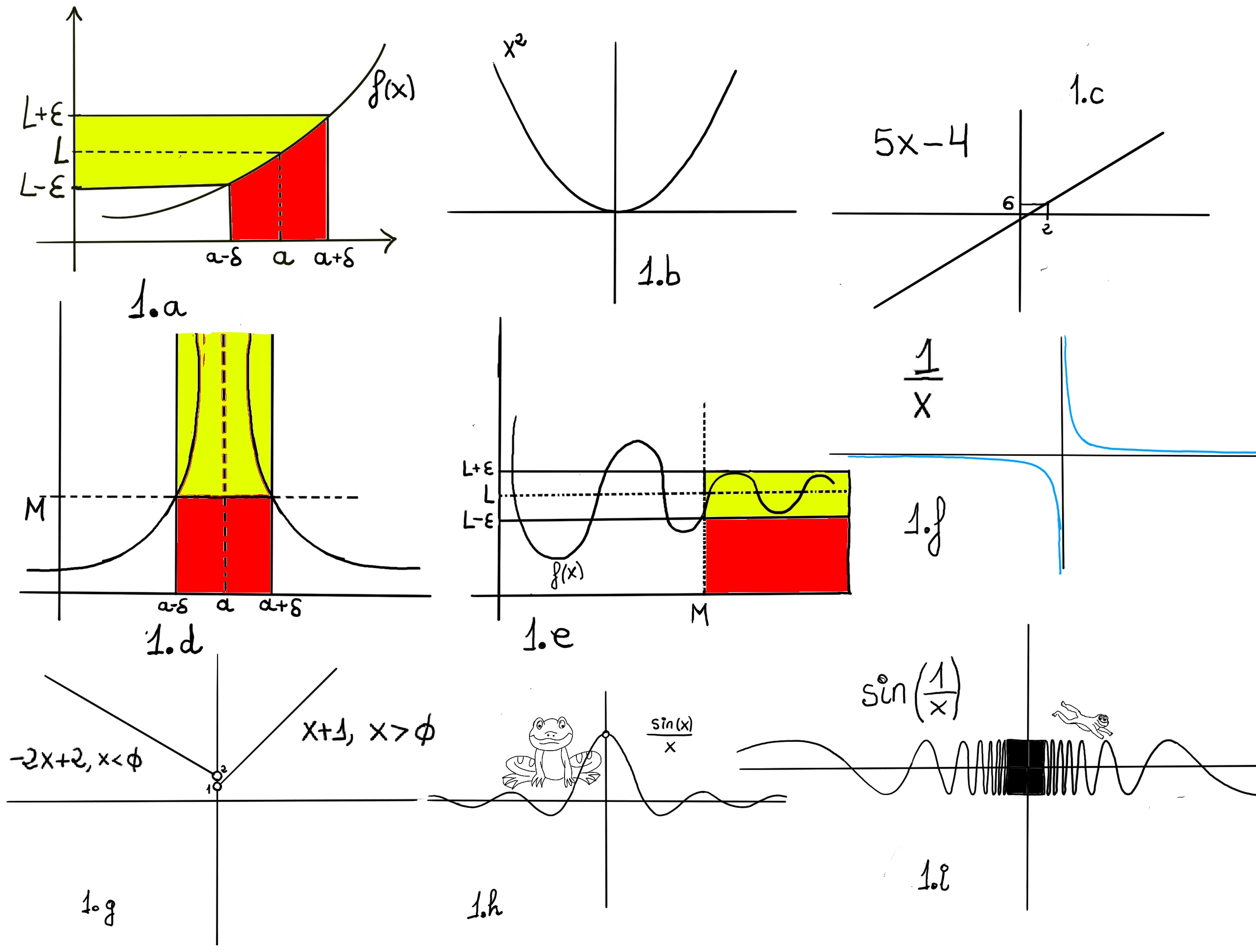
Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x)=L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$   

Definition of Rational Functions

Definition. Rational functions are ratios of two polynomial functions, f(x) = $\frac{p(x)}{q(x)} = \frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0}$ where a_n ≠ 0, b_m ≠ 0, and q(x) ≠ 0, e.g., $\frac{3-2x}{x-2}, \frac{x^3 + x^2 - 2x + 12}{x+3}.$

Limits of Rational Functions.

Let’s try to calculate $\lim_{x \to a} f(x)$:

• Direct substitution. If a ∈ Dom(f), we substitute or plug the value into the expression.

1. $\lim_{x \to 1} \frac{3-2x}{x-2} = \frac{3-2}{1-2} = -1$.
2. $\lim_{x \to 2} \frac{4x}{2x-3} = \frac{4·2}{4-3} = 8.$

• If a ∉ Dom(f) and substitution produces a zero in both denominator and numerator -indeterminate form-, it sometimes works to factor and then cancel.

1. $\lim_{x \to -4} \frac{x^2+3x-4}{x+4} = \lim_{x \to -4} \frac{(x-1)(x+4)}{x+4} = \lim_{x \to -4} (x-1) = -5$
2. $\lim_{x \to 3} \frac{x^2-x-6}{x-3} = \lim_{x \to 3} \frac{(x+2)(x-3)}{x-3} = \lim_{x \to 3} (x+2) = 5$
3. $\lim_{x \to -3} \frac{x^3 + x^2 - 2x + 12}{x+3} = \lim_{x \to -3} \frac{(x+3)(x^2-2x+4)}{x+3} = \lim_{x \to -3} (x^2-2x+4) = 9+6+4=19$

• When the expression inside the limit contains a sum or difference of fractions, it sometimes works to combine the fractions.

1. $\lim_{x \to 2} \frac{\frac{1}{x}-\frac{1}{2}}{x-2} = \lim_{x \to 2} \frac{\frac{2-x}{2x}}{x-2} = \lim_{x \to 2} \frac{-1}{2x} = \frac{-1}{4}$
2. $\lim_{x \to 2}(\frac{1}{4x-8}-\frac{1}{x^2-4}) = \lim_{x \to 2} (\frac{1}{4(x-2)}-\frac{1}{(x-2)(x+2)}) = \lim_{x \to 2} (\frac{(x+2) - 4}{4(x-2)(x+2)}) = \lim_{x \to 2} \frac{x-2}{4(x-2)(x+2)} = \lim_{x \to 2} \frac{1}{4(x+2)} = \frac{1}{16}.$
3. $\lim_{x \to 2} \frac{4}{x^2-4}-\frac{1}{x-2}$=[∞-∞] $\lim_{x \to 2} \frac{4-(x+2)}{(x-2)(x+2)} = \lim_{x \to 2} \frac{(2-x)}{(x-2)(x+2)} = \lim_{x \to 2} \frac{-1}{(x+2)} = \frac{-1}{4}.$

• The conjugate method (Rationalization). When the expression inside the limit contains a radical expression, it sometimes works to rationalize, that is, multiply numerator and denominator by a radical that will get rid of the radical in the denominator (or numerator).

1. $\lim_{x \to 0} \frac{\sqrt{1+x}-1}{x} = \lim_{x \to 0} \frac{\sqrt{1+x}-1}{x}·\frac{\sqrt{1+x}+1}{\sqrt{1+x}+1} = \lim_{x \to 0} \frac{(1+x)-1}{x(\sqrt{1+x}+1)} = \lim_{x \to 0} \frac{x}{x(\sqrt{1+x}+1)} = \lim_{x \to 0} \frac{1}{(\sqrt{1+x}+1)} = \frac{1}{2}$.
2. $\lim_{x \to 0} (\frac{3}{x\sqrt{9-x}}-\frac{1}{x})$[Combine the fractions] $\lim_{x \to 0} (\frac{3-\sqrt{9-x}}{x\sqrt{9-x}}) = \lim_{x \to 0} (\frac{3-\sqrt{9-x}}{x\sqrt{9-x}}·\frac{3+\sqrt{9-x}}{3+\sqrt{9-x}}) = \lim_{x \to 0} \frac{9-(9-x)}{(x\sqrt{9-x})(3+\sqrt{9-x})} = \lim_{x \to 0} \frac{x}{(x\sqrt{9-x})(3+\sqrt{9-x})} = \lim_{x \to 0} \frac{1}{(\sqrt{9-x})(3+\sqrt{9-x})} = \frac{1}{\sqrt{9}(3+\sqrt{9})} = \frac{1}{3·6} = \frac{1}{18}$
3. $\lim_{x \to 2} \frac{3-\sqrt{2x+5}}{x-2} = \lim_{x \to 2} \frac{3-\sqrt{2x+5}}{x-2}\frac{3+\sqrt{2x+5}}{3+\sqrt{2x+5}} = \lim_{x \to 2} \frac{9-(2x+5)}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2x+4}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2(x-2)}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2}{(3+\sqrt{2x+5})} = \frac{-2}{3+\sqrt{9}} = \frac{-2}{6} = \frac{-1}{3}$
4. $\lim_{x \to 9} \frac{x-9}{\sqrt{x}-3} = \lim_{x \to 9} \frac{(x-9)(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)} = \lim_{x \to 9} \frac{(x-9)(\sqrt{x}+3)}{x-9} = \lim_{x \to 9} \sqrt{x}+3 = \sqrt{9} + 3 = 6.$
5. $\lim_{x \to 0} \frac{1}{x\sqrt{x+1}}-\frac{1}{x} =$ [∞-∞] $\lim_{x \to 0} \frac{1-\sqrt{x+1}}{x\sqrt{x+1}} = \lim_{x \to 0} \frac{1-\sqrt{x+1}}{x\sqrt{x+1}} \frac{1+\sqrt{x+1}}{1+\sqrt{x+1}} = \lim_{x \to 0} \frac{1-(x+1)}{x\sqrt{x+1}(1+\sqrt{x+1})} = \lim_{x \to 0} \frac{-x}{x\sqrt{x+1}(1+\sqrt{x+1})} = \lim_{x \to 0} \frac{-1}{\sqrt{x+1}(1+\sqrt{x+1})} = \frac{-1}{2}$

Limits at infinite

The value of $\lim_{x \to ∞} f(x)$ can be determined by dividing the numerator and denominator by the highest power of x appearing in the denominator. This determines which term(s) in the overall expression dominate(s) the behavior of the function at large values of x.

$\lim_{x \to ∞} \frac{2x^2}{(x^2+1)(x-3)} = \lim_{x \to ∞}\frac{2x^2}{x^3-3x^2+x-3}$ =[Apply L’Hôpital’s rule or divide by x³] = $\lim_{x \to ∞}\frac{\frac{2}{x}}{1-3\frac{1}{x}+\frac{1}{x^2}-3\frac{1}{x^3}} = 0$.

$\lim_{x \to -∞} \frac{7x^3-x+2}{2x^2-5x-6}$ =[Apply L’Hôpital’s rule or divide by x²] = $\lim_{x \to -∞}\frac{7x-\frac{1}{x}+\frac{2}{x^2}}{2-\frac{5}{x}-\frac{6}{x^2}} = -∞$.

$\lim_{x \to -∞} \frac{7x^3-x+2}{2x^3-5x-6}$ =[Apply L’Hôpital’s rule or divide by x³] = $\lim_{x \to -∞}\frac{7-\frac{1}{x^2}+\frac{2}{x^3}}{2-\frac{5}{x^2}-\frac{6}{x^3}} = \frac{7}{2}$.

The limits at infinity for a rational function, say f(x) = $\frac{p(x)}{q(x)} = \frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0}$ can be exclusively determined or calculated based on its degrees:

• The degree of the numerator and the denominator are the same, $\lim_{x \to ∞} f(x) = \lim_{x \to ∞} \frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0} = \frac{a_n}{b_m}$ where m = n, a_n and b_n = b_m are the leading coefficients of p and q respectively. The line $ y = \frac{a_n}{b_m}$ is a horizontal asymptote.

1. $\lim_{x \to ∞} \frac{2x^7+4x^3+2x+1}{3x^7+4x^2+3x+5} = \lim_{x \to ∞} \frac{2x^7}{3x^7} = \lim_{x \to ∞} \frac{2}{3} = \frac{2}{3}.$
2. $\lim_{x \to ∞} \frac{4x^2+2x+7}{3x^2+3x+2} = \frac{4}{3}.$
3. $\lim_{x \to ∞} \frac{2x^5+3x^4+2x^3+7x+1}{2x^5+12x^4+3x^2+2x+8} = 1.$

• The degree of the numerator is smaller than the degree of the denominator, $\lim_{x \to ∞} f(x) = \lim_{x \to ∞} \frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0} = 0$. The line y = 0 is a horizontal asymptote.

1. $\lim_{x \to ±∞} \frac{2x^6+4x^3+2x+1}{3x^7+4x^2+3x+5} = \lim_{x \to ±∞} \frac{2x^6}{3x^7} = \lim_{x \to ±∞} \frac{2}{3x} = 0.$
2. $\lim_{x \to ∞} \frac{4x^2+2x+7}{3x^3+3x+2} =0.$
3. $\lim_{x \to ∞} \frac{2x^5+3x^4+2x^3+7x+1}{2x^7+2x^4+3x^2+2x+8} = 0.$

• The degree of the numerator is bigger than the degree of the denominator, $\lim_{x \to ∞} f(x) = \lim_{x \to ∞} \frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0} = ±∞$.

1. $\lim_{x \to ∞} \frac{2x^5+8x^2+8}{9x^3+4x^2+3x+5} = \lim_{x \to ∞} \frac{2x^5}{9x^3} = \lim_{x \to ∞} \frac{2x^2}{9} = ∞.$
2. $\lim_{x \to -∞} \frac{4x^3+2x+7}{3x^2+3x+2} = \lim_{x \to -∞} \frac{4x^3}{3x^2} = \lim_{x \to -∞} \frac{4x}{3} = -∞.$
3. $\lim_{x \to ∞} \frac{4x^3+2x+7}{3x^2+3x+2} = \lim_{x \to ∞} \frac{4x^3}{3x^2} = \lim_{x \to ∞} \frac{4x}{3} = ∞.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.