Symmetry of Graphs.

“Life is good and there’s no reason to think it won’t be, right until the moment when a blonde, non experienced nurse is going to insert a catheter in your penis like a Spanish matador,” Dad retorted. [···]

“Unless your name is Google, stop pretending you know everything. Unless your name is Facebook, stop sharing it because unless your name is Amazon, we are not buying it,” the class’ bully teased me once again, Apocalypse, Anawim, #justtothepoint.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ.

Graphing functions involves the visual representation of a curve that reflects the behavior of a mathematical function on a coordinate plane, also known as the Cartesian plane. It is a two-dimensional space defined by two axes - the x-axis (horizontal) and the y-axis (vertical).

A systematic approach to graphing a function begins by constructing a table containing selected input values and their corresponding output values. By extending this table, we can plot the points on the coordinate plane and observe the pattern they form. Connecting these points reveals the shape of the curve, allowing us to gain insights into the behavior of the function across its domain. This process provides a visual means of understanding the relationships between different variables and aids in interpreting the overall characteristics of the function.

Symmetry of Graphs

Symmetry in graphs refers to the property where certain transformations, such as reflections or rotations, result in an identical graph. There are different types of symmetry commonly observed in mathematical graphs:

1. Even functions. A function f(x) is even if f(-x) = f(x) for all the values of x in the domain, (x, y) = (-x, y) Even functions allow us to view the y-axis as a mirror, they are symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis, e.g., x², x⁴, |x|, $e^{-x^2}$ -the Gaussian function- and cos(x).

   All constant functions are even functions. The constant function f(x)=0 is both even and odd.

2. Odd functions. A function f(x) is odd if f(-x) = -f(x) for all the values of x in the domain. Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin. Some examples are x, x³, sng(x) -the sign function-, sin(x), and ¹⁄_x.

   Another way to visualize origin symmetry is to imagine a reflection about the x-axis, followed by a reflection across the y-axis.

    

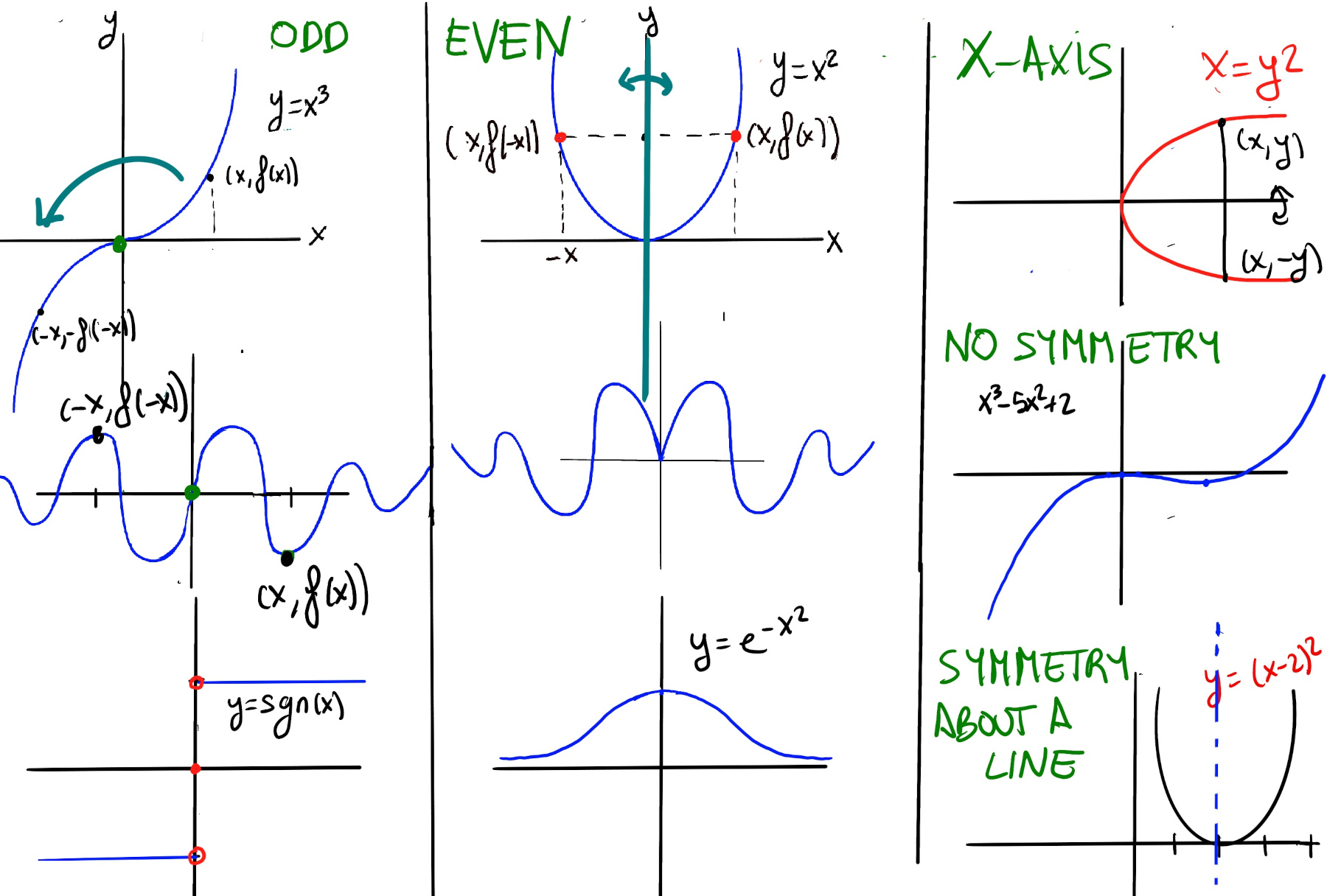
3. Symmetry with Respect to the x-axis. A graph is symmetric with respect to the y-axis if whenever a point (x, y) is on the graph, the point (x, -y) is also on the graph, e.g., x = y² ↭ y = ±$\sqrt{x}$.

   By definition, no function can be symmetric about the x-axis (or any other horizontal line), since anything that is mirrored around a horizontal line will violate the Vertical Line Test.

4. A function can be symmetric about a vertical line or about a point, e.g., y =(x-2)² is symmetric about the line x = 2, 1/x is symmetric about the lines y = x and y = -x. It is also symmetric about the origin.

   An axis of symmetry is an imaginary line that divides a figure into two identical parts that are mirror images of one another. The axis of symmetry of a parabola is the line that divides the curve into two mirror images. It passes through the center of a parabola and bisects it into two equal halves. The equation for the axis of symmetry of a parabola is y = -b/2a.

   Examples: e.g., y = (x-2)² = x²-4x +4, y = -b/2a = 4/2 = 2. x²-6x+27 is symmetric about y = -b/2a = 6/2 = 3. y = x² + 12x +32 is symmetric about y = -b/2a = -12/2 = -6.

5. No Symmetry or asymmetry. Some graphs do not exhibit any particular symmetry, e.g., f(x) = x³ -5x² +2 (f(-x) ≠ f(x), f(-x) ≠ -f(x)). Keep in mind, most graphs of equations do not have symmetry across the x-axis, y-axis, or the origin.

Test for Symmetry.

1. A function is symmetric to the y-axis if it is an even function. That is, if f(x) = f(-x). So, replace x with (-x) and simplify, e.g., f(x) = x⁴ +2x² -3. Then, f(-x) = (-x)⁴ +2(-x)² -3 = x⁴ +2x² -3 = f(x) so f is symmetric to the y-axis. However, f(x) = x³ + 2x² +x is not symmetric to the y-axis.

2. A graph will have symmetry about the y-axis if we get an equivalent equation when all the x’s are replaced with – x, e.g., e.g., y = x² we replace with y = (-x)² = x² so that y = x² is symmetric with respect to the y axis.

3. A graph will have symmetry about the origin if it is an odd function. A graph will have symmetry about the origin if we get an equivalent equation when all the y’s are replaced with –y and all the x’s are replaced with –x or, even better keep it simple, just check f(-x) = -f(x), that is, replace x with -x and simplify, e.g., f(x) = 3x³ -3x. f(-x) = 3(-x)³ -3(-x) = -3x³ + 3x = -f(x), so it is symmetric to the origin.

Examples

• Let f(x) = 3x -x³. f(-x) =-3x - (-x)³ = -3x +x³ = - (3x -x³) = -f(x), so f is an odd function, it has symmetry about the origin.The plot is shown in Figure 1.e.

• f(x) = x³ + 5x is an odd function because f(-x) = (-x)³ +5(-x) = -x³ -5x = -f(x).

• f(x) = 3x² -7 is an even function because f(-x) = 3(-x)² -7 = 3x³ -7 = f(x).

• f(x) = x² + y² = 4. To check for symmetry to the x-axis: first, it cannot be a function, since you cannot have two different y values for a given x-value in a function (it will violate the Vertical Line Test). However, if replacing y with -y gives you the same equation as the original equation, then it will be symmetric to the x-axis, e.g., y² = x or x² + y² = 4.

• x -2y = 5. If replacing y with -y gives you the same equation as the original equation, then it will be symmetric to the x-axis, x -2(-y) = 5 ↭ x +2y = 5, so it is not symmetric to the x-axis.

• x² + y² = 1 is a circle centered at the origin so it’s got symmetry about the x and y-axis and about the origin, but it is not a function.

• f(x) = -4x³ +1 is neither even nor odd and is not symmetric with respect to the y-axis. f(-x) = -4(-x)³ +1 = 4x³ +1 ≠ f(x) and ≠ -f(x).

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.