Exponential functions

“Don’t patronize me. My face makes onions and blind kids cry, vultures vomit, grannies ran past me, ghosts shiver, Medusa turn to stone, and the mother of all assholes very proud,” Apocalypse, Anawim, #justtothepoint.

The reports of my death have been greatly exaggerated, Mark Twain.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element x in a set D, x ∈ D (called the domain) exactly one element y in a set E, y ∈ E (called the codomain or range).

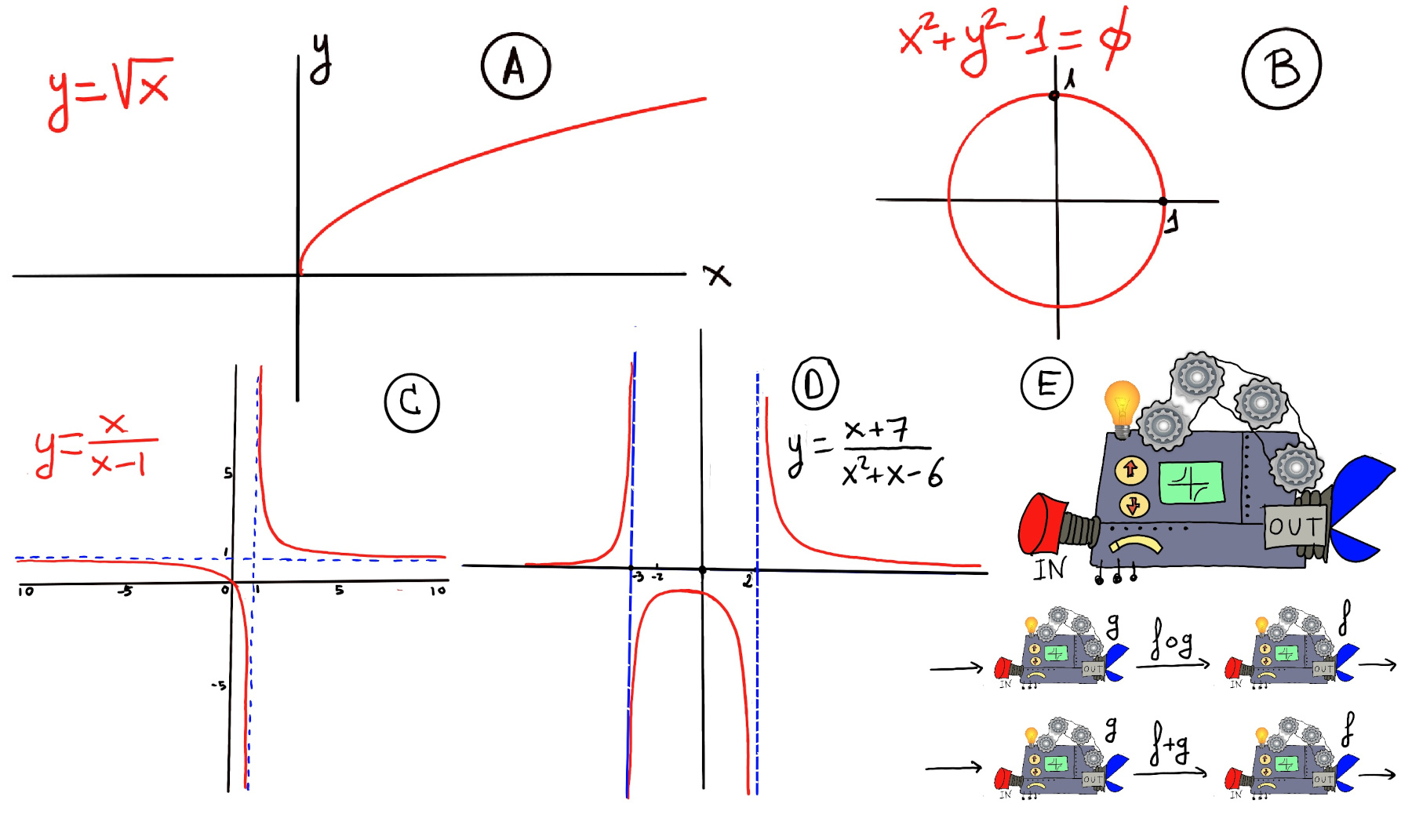
• The pair (x, y) is denoted as y = f(x) where: x is the independent variable (input) and y is the dependent variable (output). Often, both the domain D and codomain E are the set of real numbers ℝ or subsets of ℝ. A mathematical function can be thought of as a black box (or machine) that takes an input from its domain and produces exactly one output in its codomain. Inside the machine lives a specific rule (formula, procedure, or mapping) that dictates or tells you which output corresponds to each input, and a key property is uniqueness —each input maps to a single, deterministic output. No input can ever produce two different results (Figure E). The function f(x) = x² accepts any real number x (domain: ℝ) and returns exactly one non-negative value x² (output in codomain: [0,∞)). The input 3 always yields 9, never any other value.

• D is the domain, the set of all possible inputs. E is the codomain or range, the set of all possible outputs.

• Key property💡: Each input has exactly one output. (No input is assigned two different outputs — this is the vertical line test!)

• Examples: constant, f(x) = c, horizontal line, slope = 0; linear, f(x) = mx + b, straight line, constant slope m and y-intercept b; quadratic $f(x) = ax^2 + bx + c$, u-shaped or inverted U, opens up (a > 0) or down (a < 0), vertex at x = $\frac{-b}{2a}$, symmetry about vertical axis through vertex; polynomial, $f(x) = a_n x^n + \dots + a_0$, a smooth and continuous curve, n roots (counting multiplicity), end behaviour determined by its leading term $a_n x^n$; exponential function, $f(x) = a \cdot b^x, a \ne 0, b \gt 0$, rapid growth (b > 1) or decay (0 < b < 1); trigonometric functions, $\sin(x), \cos(x), \tan (z)$ oscillatory, periodic behavior (period 2π for sin/cos, π for tan), sin and cos are bounded between -1 and 1, but tan is unbounded; step function $f(x) = \lfloor x \rfloor$, greatest integer ≤ x, constant on intervals [n, n+1), jumps at integers, its graph is a staircase shape; absolute value f(x) = |x|, V-shaped graph, slope changes at 0.

• Functions can be expressed in multiple forms, each useful in different contexts: verbal description, table of values (list of pairs), algebraic formula, graph, piecewise definition, recursive definition, parametric or integral form, and series representation.

• Evaluating a function means finding or computing the output value f(x) for a given input value x. f(x) = $x^2-2x +4, f(2) = 2^2 -2\cdot 2 + 4 = 4 - 4 + 4 = 4, f(0) = 0^2 -2\cdot 0 + 4 = 4, f(1) = 1^2 -2\cdot 1 + 4 = 1 -2 +4 = 3$

• The x-intercept is any point on the graph that intersects or crosses the x-axis. In other words, it is the value of x when the function (y-coordinate or y-value) is zero. The y-intercept is the point where the graph intersects or crosses the y-axis. y-coordinate of the point whose x-coordinate is 0, e.g., 2x - 3y = 6. x-intercept: set y = 0 → 2x = 6 ⇒ x=3, so (3, 0). y-intercept: set x = 0 → −3y = 6 ⇒ y = −2, so (0, −2).

• f is said to have a local or relative maximum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≥ f(x) $∀ x \in (a, b) ∩ D$. f is said to have a local or relative minimum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≤ f(x) $∀ x \in (a, b) ∩ D$.💡Local extrema can only occur where the function stops rising or falling —either because the derivative is zero, the derivative doesn't exist, or you're at the edge of the domain.

• First Derivative Test. Let f be differentiable on an open interval containing c, except possibly at c itself, and let c be a critical point (so f′(c) = 0 or f′ is undefined). Then:

1. If f′(x) > 0 for x just to the left of c and f′(x) < 0 for x just to the right of c, then f(c) is a local maximum.
2. If f′(x) < 0 for x just to the left of c and f′(x) > 0 for x just to the right of c, then f(c) is a local minimum.
3. If f′(x) does not change sign at c (stays positive or stays negative), then f(c) is not a local extremum.

• Second Derivative Test. If the first derivate of a function at a point c is zero (f'(c) = 0) and the second derivate at this point exists, then: (i) If f''(c) > 0, then f(c) is a local minimum. (ii) If f''(c) < 0, then f(c) is a local maximum. (iii) If f''(c) = 0, the test is inconclusive.
• Vertical asymptotes are vertical lines (perpendicular to the x-axis) of the form x = a (where a is a constant) near which the function grows without bound when x approaches a from at least one side. The line x = a is a vertical asymptote of f if at least one of the one-sided limits is infinite: $\lim_{x \to a^{-}}f(x)=\pm\infty$ or $\lim_{x \to a^{+}}f(x)=\pm\infty$.
• Horizontal asymptotes are horizontal lines (y = c, parallel to the x-axis) that the graph of the function approaches as x grows very large (positively or negatively). In other words, the function values get arbitrarily close to c as long as x is sufficiently large or more formally: $\lim_{x \to \infty}f(x)=c$ and/or $\lim_{x \to -\infty}f(x)=c$.
• A line y = m+b is an oblique (slant) asymptote as $x \to \infty$ if $\lim_{x\to\infty} [f(x) - (mx+b)] = 0.$ This means that the curve of f(x) gets more and more closer to the line y = mx + b as x grows large. For an asymptote y = mx + b as $x \to \infty, m = \lim_{x\to\infty} \frac{f(x)}{x}, b = \lim_{x\to\infty} \bigl(f(x) - m x\bigr)$, provided both limits exist.

Exponential functions

A famous story —often used to illustrate exponential growth— says the ruler of India many years ago was extremely delighted with the newly created game of chess and he generously offered the inventor any reward of his choosing.

The wise man appeared humble when he asked the king for grains of wheat as a reward: a single grain of rice to be placed on the first square of the chessboard on the first day, two grains on the second square on the next day, four grains on the third, and so on, doubling the amount of grains each day until all 64 squares had been filled.

The king, quite perplexed by what appeared to be a trivial request for such a captivating game, swiftly agreed and instructed his treasurer to fulfill the agreement. However, a week later, the inventor returned to the king, inquiring about his yet-to-be-received reward. The king, infuriated by the apparent disobedience of the treasurer, promptly summoned him for an explanation.

The treasurer clarified that the stipulated sum could not be paid at all because the quantity of grains required had already surpassed the entire kingdom’s grain supply. The astounding reality is that the number of grains on the n-th square is $2^{n-1}$. Thus, on the 64th square, the number of grain required is 9,223,372,036,854,780,000 ≈ 9.22×$10^{18}$. That’s 9.223 quintillion! There isn’t enough rice in the world for this one square alone, never mind the rest of the board. Doubled growth is extremely rapid. What seems modest at the beginning becomes astronomically large soon after.

Upon absorbing this information, the king pondered the situation and eventually made a decision. In what some might consider a ruthless act, he chose to have the inventor executed. The intention behind this harsh decision was to serve as a stark lesson on the severe consequences of attempting to outsmart the king.

The exponential function is a type of mathematical function which is helpful in modelling population growth (bacteria, rabbits, humans, etc.), compound interest, radioactive decay, drug concentration in the bloodstream, spread of diseases, cancer cell growth, etc. For instance, a population of rabbits doubles every month, we would start with 2 rabbits, then 4, then 8, 16, 32, 64, 128, 256, etc! When time is measured in whole steps (like days, weeks, months or years), we get sequences like $2^n$. When time is continuous, we extend this idea to functions like $2^x$ or $e^x$, where x can be any real number. Exponential growth generally starts relatively slow but, once it gets going, it accelerates dramatically.

Definition. An exponential function is a mathematical function of the form f(x) = b·a^x, where the independent variable is the exponent, and a and b ($b\neq 0$, we want only nontrivial functions) are constants. a is called the base of the function and it should be a positive real number (a > 0).

For a = 1, we could treat it separately as a degenerate exponential, which is just the constant function f(x) = b. We normally want “exponential” to mean “genuinely growing or decaying” rather than just a constant function.

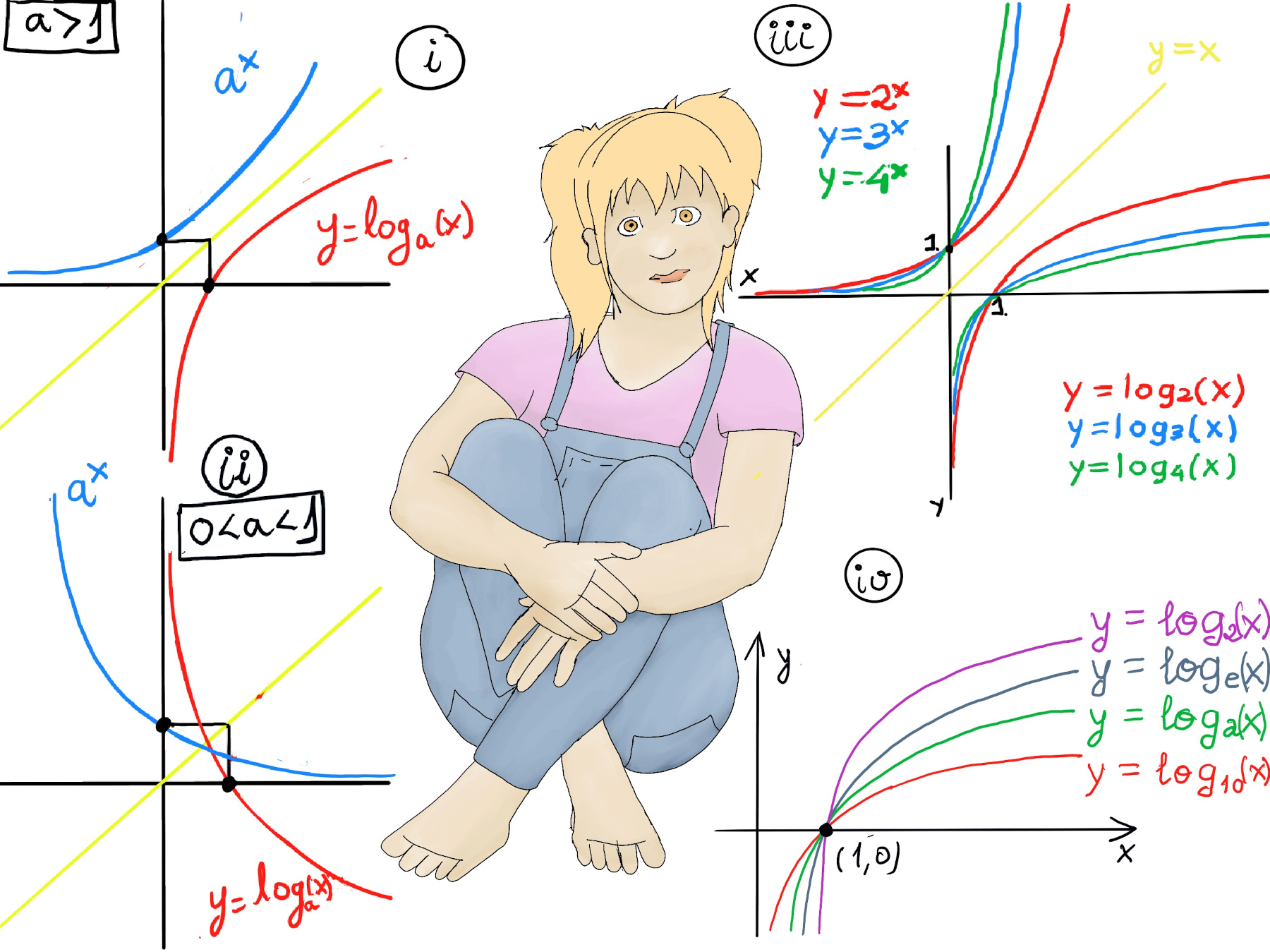
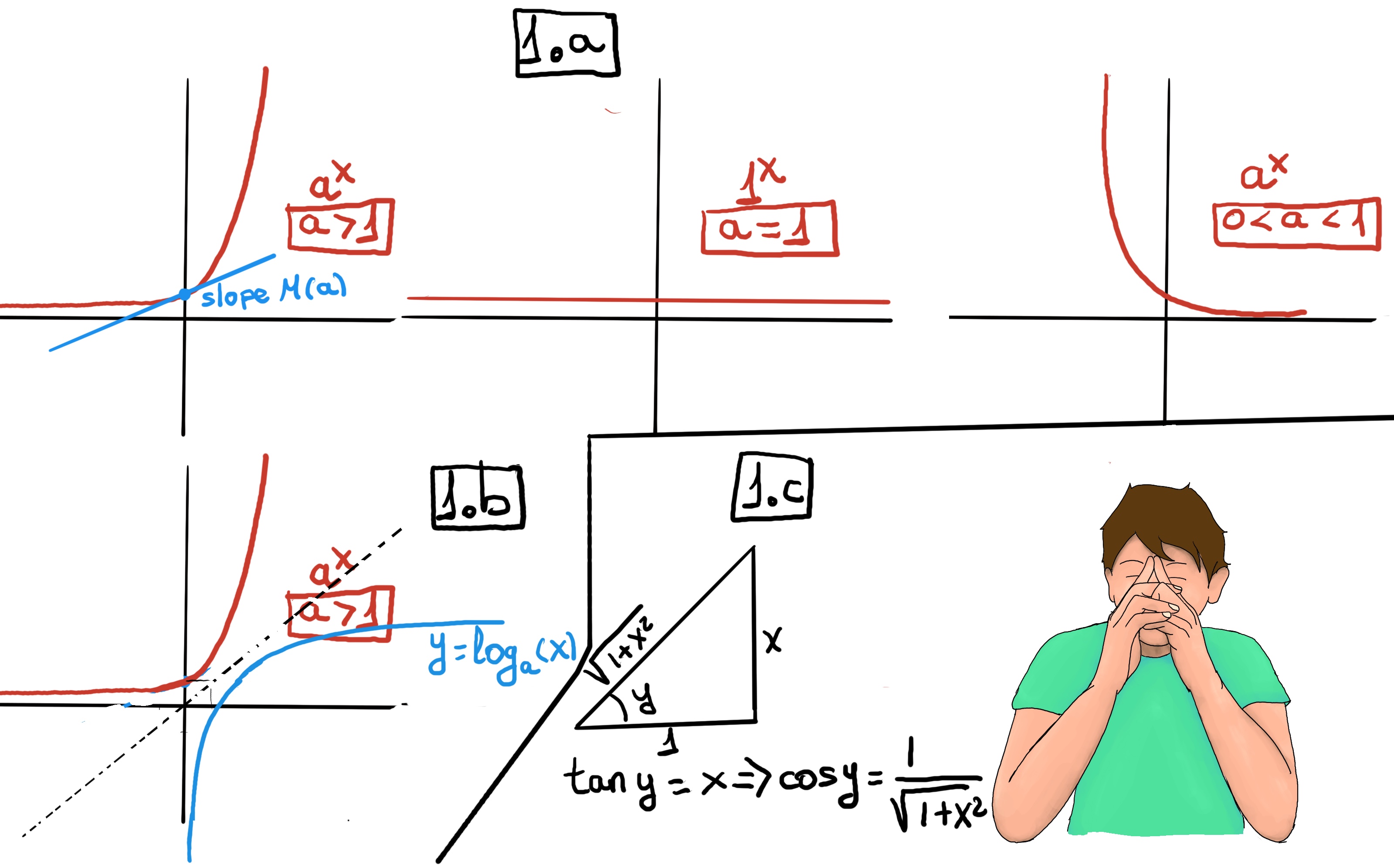
Examples are 2^x, 7^x, and (¹⁄₄)^x. There are three kinds of exponential functions depending on whether a > 1, a = 1, or 0 < a < 1 -Figure 1.a.- The more important example is the natural exponential function, f(x) = e^x where e is the Eulers Number, a mathematical constant approximately equal to 2.71828.

$\frac{d}{dx}e^x=e^x$ It’s the unique (up to scaling) function equal to its own derivative. $e=\lim _{n\rightarrow \infty }\left( 1+\frac{1}{n}\right) ^n$. Furthermore, $a^x=e^{x\ln (a)}$, so every exponential function is just a rescaled version of e^x.

1. Case a > 1. It can be observed that as the exponent increases, the curve get steeper. As x increases, f(x) heads to infinity, $\lim_{x \to ∞} a^x = ∞$. As x decreases, f(x) heads to zero, $\lim_{x \to -∞} a^x = 0$. It is strictly increasing ((e^x)’ = e^x > 0, (a^x)’ = a^x·ln(a) > 0) and has a horizontal asymptote along the x-axis.

   It is important to realize that as x approaches negative infinity, the results become very small but never actually attain zero, e.g., 2^-5 ≈ 0.03125, 2^-15 ≈ 0.00003052. Besides, the base of an exponential function determines the rate of growth or decay. For a > 1, the larger the base, the faster the function grows (Figure iii).

    
2. Case 0 < a < 1. As x increases, f(x) heads to zero, $\lim_{x \to ∞} a^x = 0$. As x decreases, f(x) heads to ∞, $\lim_{x \to -∞} a^x = ∞$. It is strictly decreasing and has a horizontal asymptote along the x-axis. $a^x=\left( \frac{1}{b}\right) ^x=b^{-x}, \text{ where } b = \frac{1}{a}>1$, decay is just growth reflected in the y-axis.
3. When a = 1, the graph is a horizontal line, y = 1. This is technically an exponential function, but it doesn’t model growth or decay, so we usually exclude a = 1 when talking about exponential growth/decay.  

Properties

1. The domain of an exponential function is the set of all real numbers, $Dom(a^x) = \mathbb{R}$.
2. It is always positive, a^x > 0, ∀x ∈ ℝ, i.e., the range is the set of all the positive real numbers, $Range(a^x) = (0, \infty)$.
3. It always intersects the y-axis at y = 1 (a⁰ = 1), that is, its graph passes through (0, 1). Furthermore, a¹ = a, in other words it also passes through (1, a).
4. Monotonicity. If a > 1, $a^x$ is strictly increasing and the function represents exponential growth. $\lim_{x \to \infty} a^x = \infty, \lim_{x \to -\infty} a^x = 0$. They have graphs that rise rapidly, e.g., 2^x, 2·3^x. If 0 < a < 1, $a^x$ is strictly decreasing and the function represents exponential decay, e.g., (¹⁄₂)^x, 7·(0.9)^x. They have graphs that decrease rapidly. $\lim_{x \to \infty} a^x = 0, \lim_{x \to -\infty} a^x = \infty$.
5. Asymptote: horizontal asymptote y = 0.
6. Exponential growth is bigger and faster than (or dominates) polynomial growth. This means that, no matter what the degree is on a given polynomial, a given exponential function will eventually grow bigger than the polynomial. Formally, for any base a > 1 and any polynomial degree k > 0, $\lim_{x \to ∞} \frac{x^k}{a^x} = 0$ (just apply l’hospital rule several times in succession. Each differentiation of the numerator reduces the degree by 1, but each differentiation of the denominator multiplies by $\ln(a)$ but keeps the exponential form).
7. Exponent rules. For any positive bases a, b > 0 and real exponents x, y, the following identities hold: a⁰ = 1, a^xa^y=a^x+y, $\frac{a^{x}}{a^{y}}=a^{x-y}$, $(a^{x})^{y}=a^{xy}=(a^{y})^{x}$, $a^{x}b^{x}=(ab)^{x}, (\frac{a}{b})^x=\frac{a^x}{b^x}$.

Exponential Function derivate and series

$\frac{d(a^x)}{dx} = \lim_{h \to 0} \frac{a^{x+h}-a^h}{h} = \lim_{h \to 0} \frac{a^xa^h-a^x}{h} = \lim_{h \to 0} \frac{a^x(a^h-1)}{h} = a^x\lim_{h \to 0} \frac{a^h-1}{h} = f'(0)·a^x$. This sucks!😞 We need to know the derivate in order to get the derivate!

Recall that e is the unique positive number for which $f'(0) = \lim_{h \to 0} \frac{e^h-1}{h} = 1$ ⇒ If f(x) = e^x ⇒ f’(x) = e^x·1 = e^x.

f(x) = a^x⇒ [a = e^ln(a)] f(x) = $(e^{lna^{x}}) = e^{(ln(a)·x)}$ ⇒[Chain Rule] f’(x) = $(e^{lna^{x}})·ln(a) = a^x·ln(a),$ hence f'(x) = $a^x·ln(a)$.

• f’(x) = $a^x·ln(a)$ and a^x > 0. If a > 1 ⇒ ln(a) > 0 ⇒ f’(x) > 0 ⇒ f is strictly increasing. If 0 < a < 1 ⇒ ln(a) < 0 ⇒ f’(x) < 0 ⇒ f is strictly decreasing.

• The derivative of the exponential function is the function itself, $(e^{x})'=e^x$ ⇒ e^x > 0, The exponential is strictly increasing.

• $e^x =$[Taylor Series] $\sum_{n=0}^\infty \frac{(x-a)^n}{n!}f^{n}(a)$ =[a = 0, $(e^{x})'=e^x$, e⁰ = 1] $\sum_{n=0}^\infty \frac{x^n}{n!}$. In particular, e = $\sum_{n=0}^\infty \frac{1}{n!}$

Exercises

• Simplify the expression $\frac{27^{2x-3}}{9^{x-4}}$.

$\frac{27^{2x-3}}{9^{x-4}} = \frac{3^{3^{2x-3}}}{3^{2^{x-4}}}$ ⇒[$(a^{x})^{y}=a^{xy}=(a^{y})^{x}$] $\frac{3^{3(2x-3)}}{3^{2(x-4)}} = \frac{3^{6x-9}}{3^{2x-8}}$ ↭[$\frac{a^{x}}{a^{y}}=a^{x-y}$] = $3^{6x-9-(2x-8)} = 3^{4x-1}$

• Solve the equation, (1/4)^x = 64.

(1/4)^x = 64 ↭[$(\frac{a}{b})^x=\frac{a^x}{b^x}$] $\frac{1^x}{4^x} = 64↭ 4^{-x} = 4^3$ ⇒[a = 4 > 1, the exponential is strictly increasing (⇒ one-to-one)] x = -3.

• Solve the equation, 32^(x/3) = 8^(x-12).

$32^{\frac{x}{3}} = 8^{x-12} ↭ 2^{5^{(\frac{x}{3})}} = 2^{3^{(x-12)}}$ ⇒[$(a^{x})^{y}=a^{xy}=(a^{y})^{x}$] $2^{\frac{5x}{3}}=2^{3(x-12)}$ ⇒[a = 2 > 1, the exponential is strictly increasing (⇒ one-to-one)] $\frac{5x}{3} = 3(x-12)↭ 5x = 9(x-12) ↭ 5x = 9x -108 ↭ 4x = 108 ↭ x = \frac{104}{4} = 27.$

• Solve the equation, 3^2x -6·3^x -27 = 0.

Notice that $3^{2x} = 3^{x^{2}}$ ⇒ the given equation is a quadratic equation, let y = 3^x, y² -6y -27 = (y +3)(y -9) = 0 ⇒ There are two options y = -3 or y = 9 ⇒ $3^x = -3⊥, 3^x = 9$ ⇒ x = 2.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.