Conservative vector field

Learn everything you can, anytime you can, from anyone you can – there will always come a time when you will be grateful you did, Sarah Caldwell.

Enjoy the little things, for one day you may look back and realize they were the big things, Robert Brault.

Conservative vector field

The gradient of a scalar function f is a vector that points in the direction of the greatest rate of increase of the function, and its magnitude represents the rate of change in that direction. ∇f = ($\frac{∂f_1}{∂x_1},\frac{∂f_1}{∂x_2},$) where $\frac{∂f_1}{∂x_i}$ denotes the partial derivative of f with respect to the i-th variable.

A conservative vector field is a vector field that is the gradient of some function, say $\vec{F}$ = ∇f. This scalar function is referred to as the potential function or potential energy function associated with the vector field.

In this case, we can simplify the evaluation of $\int_{C} \vec{F}dr$

Theorem. Fundamental theorem of calculus for line integral. If f is a conservative vector field in a simply connected region of space (i.e., a region with no holes), and if f is a scalar potential function for F in that region, then $\int_{C} ∇f·dr = f(P_1)-f(P_0)$ where P₀ and P₁ are the initial and final points of the curve C, respectively.

Proof:

$\int_{C} ∇f·dr = \int_{C}\frac{∂f}{∂x}dx + \frac{∂f}{∂y}dy = $[Notation^] $\int_{C}f_xdx + f_ydy$ and we want to parametrize the trajectory C, x = x(t), y = y(t), t₀≤ t ≤ t₁, dx = x’(t)dt, dy = y’(t)dt

$\int_{C} ∇f·dr =\int_{C}f_xdx + f_ydy = \int_{C}f_xdx + f_ydy =\int_{C} (f_x\frac{dx}{dt}+f_y\frac{dy}{dt})dt$ =[The Chain Rule] $\int_{C} \frac{df}{dt}dt = \int_{t_0}^{t_1} df$ =[The fundamental Theorem of Calculus] =$f(x(t), y(t))\bigg|_{t_0}^{t_1} = f(P_1)-f(P_0)$

Recall our previous exercise $\vec{F}= y\vec{i}+x\vec{j}$ = ⟨x, y⟩ amd we want the work done as we move along C = C₁+ C₂ + C₃ in the unit circle (Figure D)

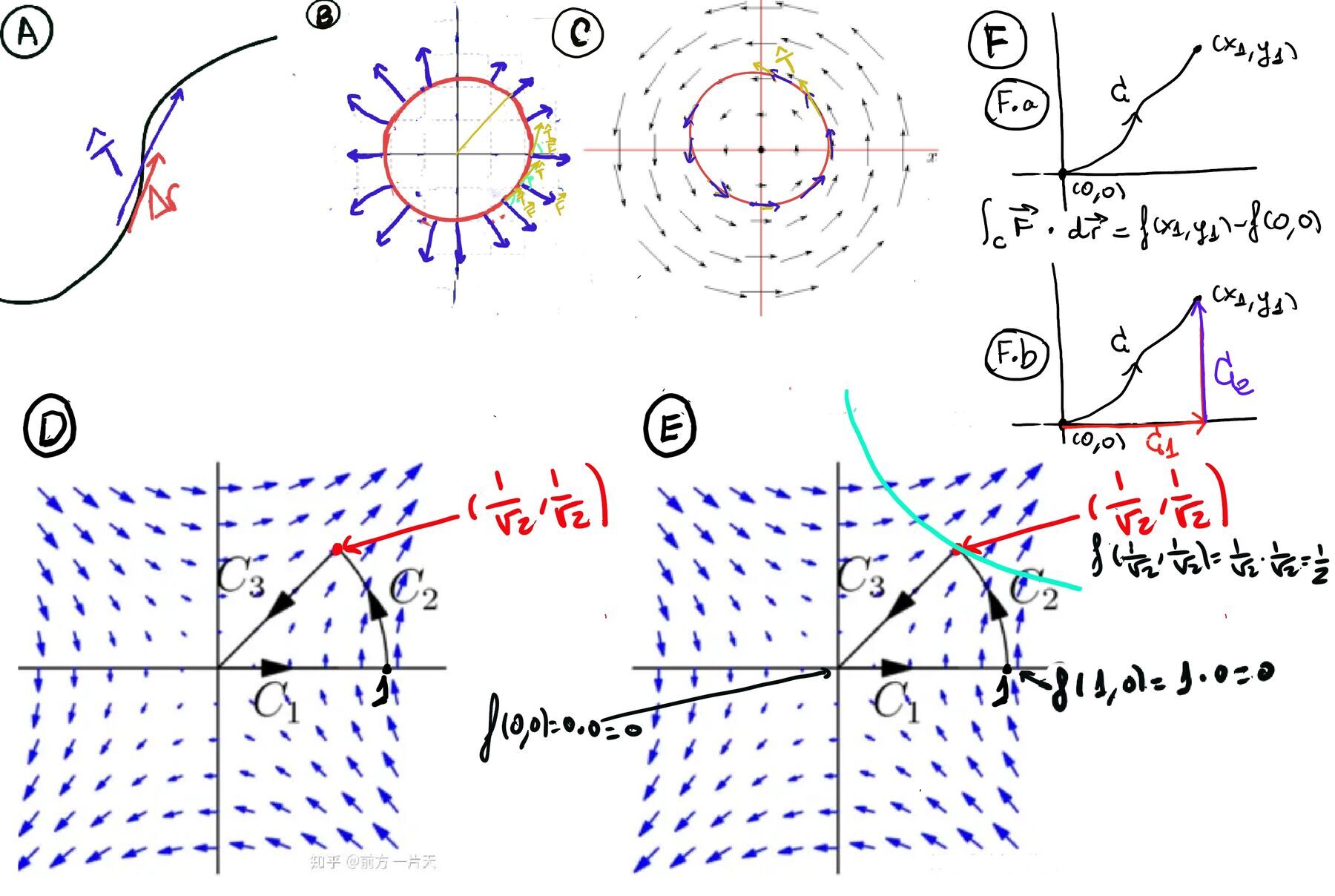
The main idea is that $\vec{F}= ∇f$ where f(x, y) = xy, and $\int_{C} ∇f·dr = f(P_1)-f(P_0)$ =[Figure E] 0 -0 = 0. In particular, $\int_{C_2} \vec{F}·d\vec{r} = f(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})-f(1,0) = \frac{1}{2}-0 = \frac{1}{2}.$

The significance and main idea of conservative vector fields lies in their path independence, which means that the work done by the vector field along any path between two points depends only on the endpoints and not on the path taken, $\int_{C_1} ∇f·dr = \int_{C_2} ∇f·dr$ as long as C₁ and C₂ have the same start and end points.

In general, the work done by a conservative vector field is zero along any closed curve C, $\int_{C} ∇f·dr = f(EndPoint)-f(OriginPoint) = 0$ because both points are the same point.

• Counterexample. Recall the previous example. Let $\vec{F} = -y\vec{i}+x\vec{j}$, and the curve x = t, y = t², 0 ≤ t ≤ 1 (Figure 4.a, C is the blue parabola).

W = $\int_{C} \vec{F}·d\vec{r} = \int_{C} \vec{F}·\hat{\mathbf{T}}ds =$ [$\vec{F}//\hat{\mathbf{T}}⇒\vec{F}·\hat{\mathbf{T}} = |\vec{F}|$] = $\int_{C} |\vec{F}|ds = \int_{C} 1·ds$ =[C is the unit circle] 2π ≠ 0, so it is not a conservative field ↭ no path independence ↭ $\vec{F}$ is not a gradient of any function.

Application

If the force $\vec{F}$ acting on an object is the gradient of a potential function, $\vec{F} = ∇V$, then the work done by this force on the object is indeed equal to the change in the value of the potential function.

This relationship could be expressed using the fundamental theorem of calculus for line integrals. Let C be a smooth curve in space along which the object that moves under the influence of the force $\vec{F}$. If P₁ and P₂ are two points on the curve C with position vectors $\vec{r_1}~\text{and}~\vec{r_2}$respectively, then the work done by $\vec{F}$ as the object moves from P₁ to P₂ = $\int_{C} \vec{F}·d\vec{r} =$ [By the fundamental theorem of calculus for line integral, $\vec{F} = ∇V$ ] = $V\vec(r_2)-\vec(r_1)$

In other words, the work done by the force $\vec{F}$ is equal to the difference in the values of the potential function V evaluated at the final and initial positions of the object.

In both gravitational and electrical systems, the total energy is conserved (Conservation of energy). It states that the total energy of a closed system remains constant over time. More precisely, g = -∇V where g is the gravitational field (the force experienced by objects due to gravity ≈ 9.8 m/s² directed downwards) and V is the gravitational potential.

A force $\vec{F}$ is considered conservative ( $\int_{C} \vec{F}·d\vec{r} = 0$ along all closed curves C) if and only if it is path-independent (the work done by the force in moving an object from one point to another is the same, regardless of the path taken).

This statements holds true. If $\vec{F}$ is path-independent and I consider a closed curve, path independence tells me instead of going all around, I just may prefer stay where I am, and then, the work would be just zero. Conversely, if $\vec{F}$ is conservative, I have two points P₁, P₂ and two paths between them, C₁ and C₂ respectively, but this implies that C₁ -C₂ is a closed path (I come back to my original point P₁). $\vec{F}$ is conservative ⇒ $\int_{C_1-C_2} \vec{F}·d\vec{r} = 0 ⇒ \int_{C_1-C_2} \vec{F}·d\vec{r} = \int_{C_1} \vec{F}·d\vec{r} -\int_{C_2} \vec{F}·d\vec{r} =0 ⇒ \int_{C_1} \vec{F}·d\vec{r} = \int_{C_2} \vec{F}·d\vec{r}.$

If $\vec{F}$ is conservative, $\vec{F} = ∇f$ where F = ⟨M, N⟩ = $⟨\frac{∂f}{∂x}, \frac{∂f}{∂y}⟩ = ⟨f_x, f_y⟩$ represents a vector field in two dimensions, f is the potential function associated with the vector field $\vec{F}$, and $\int_{C} \vec{F}·d\vec{r}$ is the line integral of the vector field $\vec{F}$ along the path C and measures the work done by the vector field in moving an object along the path C. Then, $\int_{C} \vec{F}·d\vec{r} = Mdx +Ndy$.

We already know that f_xy = f_yx ⇒[A criteria to check that $\vec{F}$ is conservative] M_y = N_x. Conversely, if $\vec{F}$ = ⟨M, N⟩, M_y = N_x, and it is defined and differentiable everywhere, then $\vec{F}$ is conservative (a gradient field) -we are not going to prove this last statement-.

Recall the previous example. Let $\vec{F} = -y\vec{i}+x\vec{j}$, and C is the unit circle, we are going to check that this vector is not a gradient. M = -y, N = x, and we see that $\frac{∂M}{∂y} = -1 ≠ 1 = \frac{∂N}{∂x}$.

Exercise. Let $\vec{F}=(4x^2+axy)\vec{i}+(3y^2+4x^2)\vec{j}$, what value of a makes $\vec{F}$ a gradient. M = 4x²+axy, N = 3y²+4x². M_y = ax, N_x = 8x, ax =8x ↭ a = 8.

Finding a potential function for conservative vector fields

First, ensure that the field you are dealing with is conservative. We introduce the procedure for finding it via an example, the vector field previously studied $\vec{F}= (4x^2+8xy)\vec{i}+(3y^2+4x^2)\vec{j}$. There are two methods.

One is computing line integrals. Let’s suppose that C is a trajectory between the origin (0, 0) and (x₁, y₁) -Figure F.a-, and let’s compute $\int_{C} \vec{F}·d\vec{r} = f(x_1, y_1) -f(0, 0) ⇒ f(x_1, y_1) = \int_{C} \vec{F}·d\vec{r} + f(0, 0)$ where f(0, 0) is just a constant.

It is far easy to compute the integral by diving C into two path, one C₁ along the x-axis (from (0, 0) to (x₁, 0)) and a second one C₂ parallel to the y-axis (from (x₁, 0) to (x₁, y₁)) -Figure F.b-.

$\vec{F}=⟨4x^2+8xy, 3y^2+4x^2⟩ ⇒ \int_{C} \vec{F}·d\vec{r} = \int_{C} (4x^2+8xy)dx + (3y^2+4x^2)dy = \int_{C_1} (4x^2+8xy)dx + (3y^2+4x^2)dy + \int_{C_2} (4x^2+8xy)dx + (3y^2+4x^2)dy$

$\int_{C_1} (4x^2+8xy)dx + (3y^2+4x^2)dy$ = [0 ≤ x ≤ x₁, y = 0 ⇒ dy = 0] $\int_{0}^{x_1} 4x^2dx =\frac{4}{3}x_1^3$

$\int_{C_2} (4x^2+8xy)dx + (3y^2+4x^2)dy$ = [0 ≤ y ≤ y₁, x = x₁ ⇒ dx = 0] $\int_{0}^{y_1} (3y^2+4x_1^2)dy = (y^3+4x_1^2y)\bigg|_{0}^{y_1} = y_1^3+4x_1^2y_1$

$f(x_1, y_1) = \int_{C} \vec{F}·d\vec{r} + f(0, 0) ⇒ f(x_1, y_1) = \int_{C} \vec{F}·d\vec{r} + c ↭ f(x, y) = \int_{C} \vec{F}·d\vec{r} + c = \frac{4}{3}x^3 + y^3+4x^2 + c$.

The second method is to use antiderivatives and we will use the same example [Recall If $\vec{F}$ is conservative, $\vec{F} = ∇f$ where F = ⟨M, N⟩ = $⟨\frac{∂f}{∂x}, \frac{∂f}{∂y}⟩ = ⟨f_x, f_y⟩$] where f_x = 4x^2 +8xy (i), f_y = 3y² +4x² (ii).

(1) ⇒ f = $\frac{4}{3}x^3+4x^2y+g(y)$. g(y) is a constant for x, but not necessarily for y ⇒[(ii)] f_y = 4x² + g’(y) = 3y² +4x² ⇒ g’(y) = 3y² ⇒ g(y) = y³ +c and c is a real constant.

Therefore, f = $\frac{4}{3}x^3+4x^2y+g(y) = \frac{4}{3}x^3+4x^2y+ y^3 +c$

Recall that If $\vec{F}$ is conservative, $\vec{F} = ∇f$ where F = ⟨M, N⟩ = $⟨\frac{∂f}{∂x}, \frac{∂f}{∂y}⟩ = ⟨f_x, f_y⟩$ represents a vector field

Definition. Given the vector field $\vec{F}$, the curl is defined to be $curl(\vec{F}) = N_x - M_y$

Test of conservatiness. A vector field $\vec{F}$ is said to be conservative if $curl(\vec{F}) = N_x - M_y$ = 0.

A physical interpretation of the curl us is as follows. Suppose that $\vec{F}$ is a velocity field, then $curl(\vec{F})$ represents the rotation component of the motion, e.g., $\vec{F} = ⟨a, b⟩$ where a and b are constants, $curl(\vec{F}) = 0.$; $\vec{F} = ⟨x, y⟩, curl(\vec{F}) = N_x - M_y = \frac{∂}{∂x}(y) - \frac{∂}{∂y}(x) = 0 -0 = 0; \vec{F} = ⟨-y, x⟩, curl(\vec{F}) = N_x - M_y = \frac{∂}{∂x}(x) - \frac{∂}{∂y}(-y) = 1 +1 = 2$ ↭ we are rotating, that is, curl measures 2x angular velocity of the rotation component of the velocity field (Figures 1, 2, and 3 respectively).

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.