
|
 |
 |
|
 |
When you have eliminated the impossible, whatever remains, however improbable, must be the truth, Sherlock Holmes
Theorem: Let f(x) be the general nth degree polynomial in F[x] of deg(f) = n ≤ 4, then f is solvable (by radicals).

Mod p Irreducible Test. Let p be a prime and suppose that f(x)∈ ℤ[x] with deg f(x) ≥ 1. Let f′(x) be the polynomial in ℤp[x] obtained from f(x) by reducing all the coefficients of f(x) modulo p. If f′(x) is irreducible over ℤp and deg f(x)= deg f′(x), then f(x) is irreducible over ℚ.
Resolvent cubic is a cubic polynomial defined from a monic polynomial of degree four, g(x) = (x -β1)(x -β2)(x -β3) ∈ K[x]. We define β1 = α1α2 + α3α4, β2 = α1α3 + α2α4, β3 = α1α4 + α2α3, βi∈ K.
| D square ∈ F | D square ∉ F | |
|---|---|---|
| g is reducible over F | D2 | G = D4 or G = C4 |
| g is irreducible over F | G = A4 | G = S4 |
Corollary. If g splits completely in F ↭ G = D2. If g has exactly one root in F ↭ G = D4 or C4. g is irreducible ↭ G = S4 or A4
Disc(x4 +cx +d) = 256d3 -27c4. Resolvent cubic of x4 +cx + d = x3 -4dx -c2
K = $ℚ(\sqrt[4]{2}, \sqrt[4]{2}i) = ℚ(\sqrt[4]{2}, i)$, and this can be easily seen because i = $\frac{i\sqrt[4]{2}}{\sqrt[4]{2}}$ so $ℚ(\sqrt[4]{2}, i) ⊆ ℚ(\sqrt[4]{2}, \sqrt[4]{2}i)$, but obviously it is also the case that $\sqrt[4]{2}i = \sqrt[4]{2}·i$ so $ℚ(\sqrt[4]{2}, \sqrt[4]{2}i) ⊆ ℚ(\sqrt[4]{2}, i)$.
$β_1 = 2i\sqrt{2}, β_2=0, β_3=-2i\sqrt{2}, g = (x -2i\sqrt{2})(x + 2i\sqrt{2})x = x^3+8x$, g is reducible, and has exactly one root in ℚ ⇒ Gal(f) = D2 (it is not possible because it is not completely reducible -Corollary-) D4 or C4. To discriminate between these two choices, further analysis is required.
Therefore, [K: ℚ] = [K : ℚ(i, ∜2)]·[ℚ(∜2) : ℚ] = 8 ⇒ Gal(f) = D4.
The dihedral group D4 is the symmetry group of the square. D4 = ⟨r, s : r4 = s2 = id, rs = sr-1⟩.
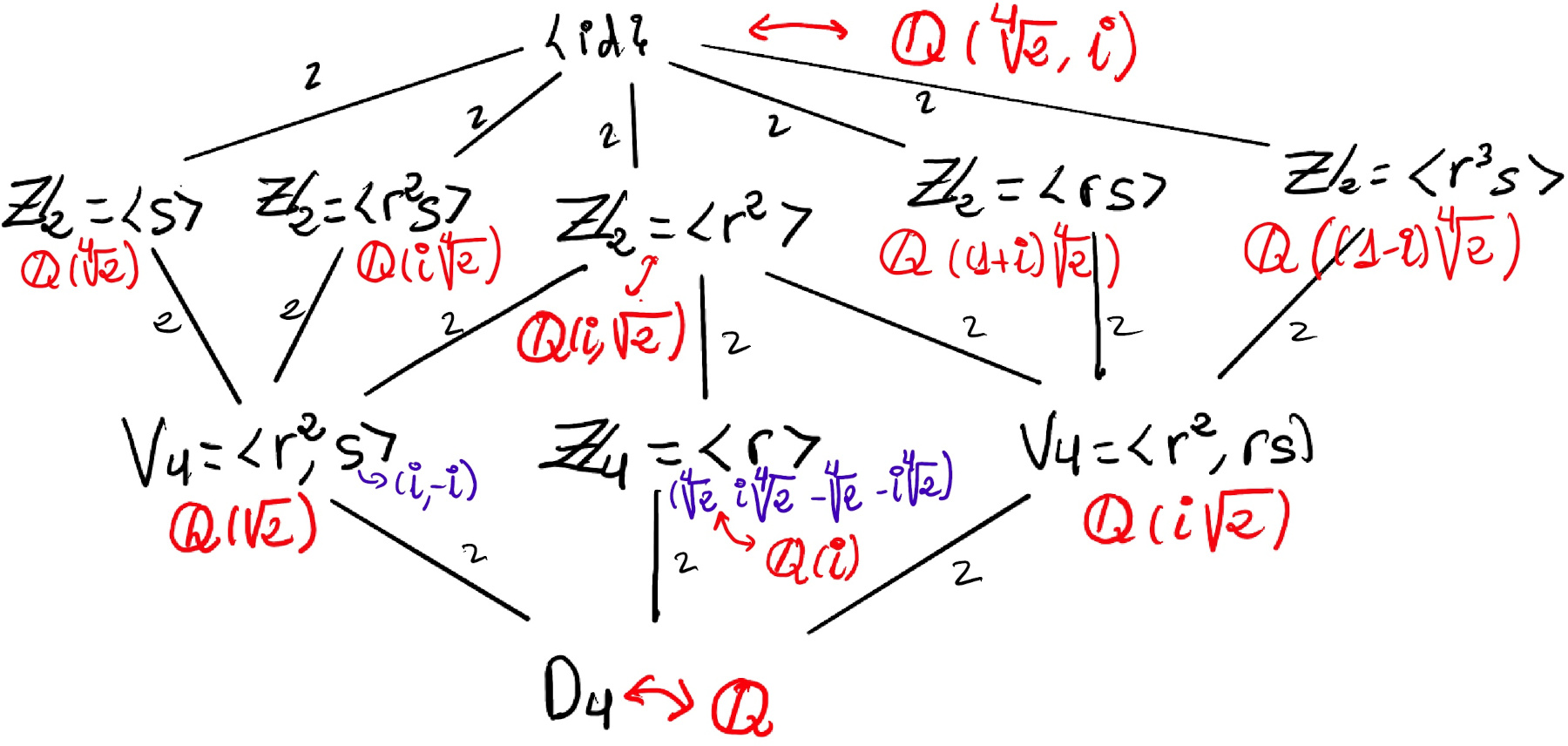
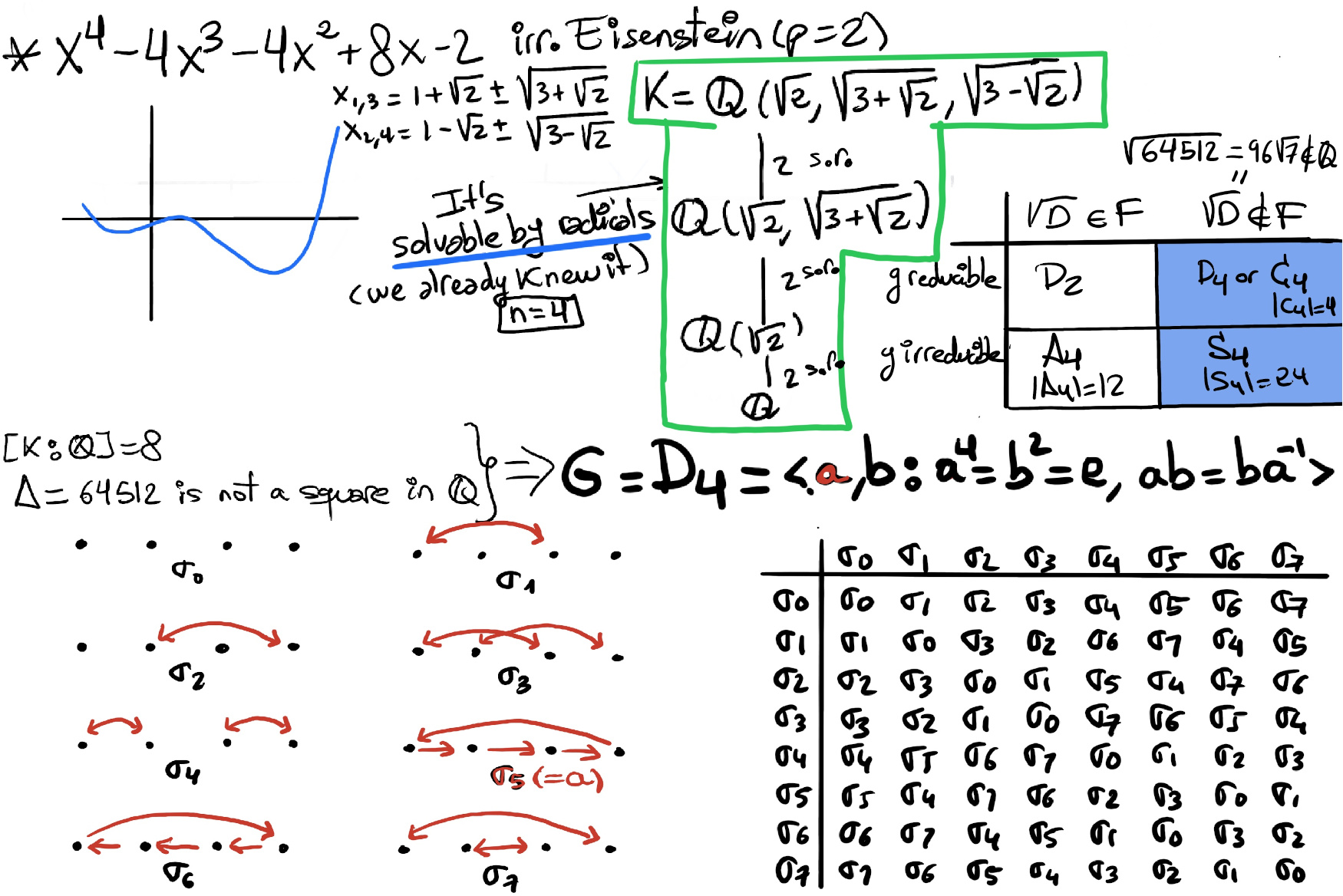
Since [K : ℚ] = 8, and Δ is not a square in F (G = D4, C4 -|C4| = 4, or S4 -|S4| = 24), the only option with order 8 is D4 = ⟨a, b: a4 = b2 = e, ab = ba-1⟩.
It is obviously solvable by radicals: $\mathbb{Q}⊆\mathbb{ℚ}(\sqrt{2})⊆{ℚ}(\sqrt{2},\sqrt{3+\sqrt{2}})⊆{ℚ}(\sqrt{2},\sqrt{3+\sqrt{2}},\sqrt{3-\sqrt{2}})$

f(x) = x4 +1, roots: ±1, ±i, g = x3 -4x. g is completely reducible in ℚ, its roots are -2, 0, and 2 ⇒ Gal(f) = D2. Another way of obtaining the same result is seeing that K = ℚ(i), [K : ℚ] = 2, K/ℚ ≋ D2.
f(x) = x4 -16x2 + 4. It is irreducible modulo 3 (or over ℤ3, Mod p Irreducible Test) ⇒ f is irreducible in ℚ[x]. Its discriminant (Disc(f) = Disc(g) = ) Δ = 19202, so $\sqrt{Δ} = 1920 ∈ \mathbb{Q}$. Futhermore, the resolvent is g = x3 -128x2 +3840x, so it is reducible over ℚ ⇒ Gal(K/Q) ≋ D2.
f(x) = x4 -4x2 +2, is irreducible by Eisenstein, p = 2 | -4, 2 |2, but 2 ɫ an = 1, p2 = 22 = 4 ɫ a0 = a2
x4 -4x2 +2 = (x4 -4x +4) -2 = (x2-2)2 -2 = 0 ⇒ (x2-2)2 = 2 ⇒ $(x^2-2)=±(\sqrt{2}) ⇒ x^2 = 2±(\sqrt{2})$ ⇒ Its roots are $±α = ±\sqrt{2+\sqrt{2}}, ±β = ±\sqrt{2-\sqrt{2}}.$ Notice that β = $\frac{α^2-2}{α}∈ℚ(α)$, so K = [🚀] $ℚ(α)=ℚ(\sqrt{2+\sqrt{2}})$. An automorphism Φ: ℚ(α) → ℚ(α) is defined by permuting the four roots, e.g., σ: α → β, β → -α, Gal(K/ℚ) ≋ [Since [K : ℚ] = 4, the options with order 4 are Gal(K/ℚ) ≋ D2 or C4] D2 or C4
🚀 ℚ(α) = $ℚ(\sqrt{2+\sqrt{2}}), β = \sqrt{2-\sqrt{2}} = \frac{(\sqrt{2-\sqrt{2}})·(\sqrt{2+\sqrt{2}})}{(\sqrt{2+\sqrt{2}})}=\frac{\sqrt{2}}{\sqrt{2+\sqrt{2}}}$. It is obvious that α ∈ ℚ(α) = $ℚ(\sqrt{2+\sqrt{2}}) ⇒ α^2 = 2 + \sqrt{2} ∈ ℚ(α) ⇒ \sqrt{2} ∈ ℚ(α) ⇒ β = \frac{\sqrt{2}}{\sqrt{2+\sqrt{2}}} ∈ ℚ(α)$ ⇒ K = ℚ(±α, ±β) = ℚ(α).
Let σ be defined by σ: α → β, β → -α. σ2(α) = σ(β) = -α, σ3(α) = σ(-α) = -β, σ4(α) = σ(-β) = α. σ2(β) = σ(-α) = -β, σ3(β) = σ(-β) = α, σ4(β) = σ(α) = β ⇒ σ4 = id ⇒ σ has order 4 ⇒ [D2 has all elements of order 2 except the identity, but C4 has an element of order 4] Gal(K/Q) ≋ C4.
x4 +4x2 +2 = 0 ↭ $x^4 +4x^2 +4 -2 = 0 ↭ (x+2)^2 = 2 ↭ x = ±\sqrt{-2 ±\sqrt{ 2 }}, α_1 = \sqrt{-2 +\sqrt{ 2 }}, α_2 = -\sqrt{-2 +\sqrt{ 2 }}, α_3 = \sqrt{-2 -\sqrt{ 2 }}, α_4 = -\sqrt{-2 -\sqrt{ 2 }}$
By a similar reasoning than before K = ℚ(α1) because $α_1^2 = -2 + \sqrt{2} ∈ K ⇒ \sqrt{2} ∈ K$. Futhermore, α1α3 = $(\sqrt{-2 +\sqrt{ 2 }})(\sqrt{-2 -\sqrt{ 2 }}) = i(\sqrt{2 -\sqrt{ 2 }})i(\sqrt{2 +\sqrt{ 2 }}) = -\sqrt{2} ⇒ α_3 = \frac{-\sqrt{2}}{α_1} ∈ K, α_4 = -α_3 ∈ K$, so K is the splitting field of the irreducible polynomial f over ℚ ⇒ [K : ℚ] = deg(f) = 4 = |Gal(f)|. Since [K : ℚ] = 4, the options with order 4 are Gal(K/ℚ) ≋ D2 or C4
Next, σ ∈ Gal(f), σ(α1) = α3 is an element of order 4 ⇒ [D2 has all elements of order 2 except the identity, but C4 has an element of order 4] Gal(K/Q) ≋ C4.
Besides, the discriminant is Δ = 2048, so $\sqrt{Δ}∉\mathbb{Q}$, and the resolvent is g = x3 +32x2 + 128x which is reducible over ℚ ⇒ Gal(K/ℚ) ≋ D2 or C4.
f(x) = x4 -x -1 ∈ ℚ[x], f(x) = x4 -x -1 is irreducible modulo 2 (Mod p Irreducible Test, 0-0-1=-1≠0, 1-1-1=-1≠0) ⇒ f is irreducible in ℚ[x]. [Disc(x4+ cx +d) = 256d3 -27d4. Resolvent cubic(x4+ cx +d) = x3 -4dx -d2] Disc(f) = -283 is not a square in ℚ, g = x3 +4x -1 ∈ ℚ[x] is irreducible [By rational root test, any root must be ±1, but none of them are roots] ⇒ g is irreducible, Disc(f) is not a square ⇒ Gal(f) ≋ S4.
f(x) = x4 + x3 + 1. It is irreducible modulo 2 or over ℤ2 (Mod p Irreducible Test) ⇒ f is irreducible over ℚ. Disc(f) = 229 is not a square in ℚ, g = x3 -3x2 -61x -1 ∈ ℚ[x] is irreducible [By rational root test, any root must be ±1, but none of them are roots] ⇒ g is irreducible, Disc(f) is not a square ⇒ Gal(f) ≋ S4.
f(x) = x4 +8x + 12 ∈ ℚ[x] is irreducible (not easy). Disc(f) = 576, $\sqrt{576}=24∈ ℚ$. The resolvent is g = x3 -48x -64, g’= [g modulo 5] x3 -3x -4 = x3 + 2x +1 is irreducible modulo 5: 0+0+1=1≠0, 1+2+1=4≠0, 8+2+1=1≠0, 27+6+1=34=4≠0, 64+8+1=73=3≠0 ⇒ g is irreducible in ℚ and Disc(f) ∈ ℚ ⇒ Gal(f) ≋ A4.
f(x) = x4 +24x +36 ∈ ℚ[x] is irreducible modulo 17 or over ℤ17 (Mod p Irreducible Test, tedious 😞). Disc(f) = 17282, $\sqrt{Δ}=1728 ∈ ℚ$. The resolvent g is g = x3 -2304x -36864 is irreducible modulo 3 or over ℤ3 ⇒ g is irreducible in ℚ and Disc(f) ∈ ℚ ⇒ Gal(f) ≋ A4.
f(x) = x6 -2x5 -x4 +4x2 +2x -4 = (x3-2)(x -1)(x +1)(x -2) so it has three roots in ℚ (namely 1, -1, and 2) and two non-real-roots ⇒ [Insolvability of quintics II Let f ∈ ℚ[x] be an irreducible polynomial of prime degree p with exactly one pair of non-real complex conjugate roots. Then, f is not solvable by radicals, G ≋ ℤp] Gal(f) = S3
f(x) = x5 -7 is irreducible over ℚ (Eisenstein criteria). This is based on an exercise on Fields and Galois Theory, John. M. Howie, Springer. The primitive root w = $e^{\frac{2πi}{5}}$ has minimum polynomial x4 +x3 + x2 +x +1 ⇒ |ℚ(w) : ℚ| = 4.
Futhermore, x5 -7 is irreducible over ℚ(w). Suppose for the sake of contradiction, x5 -7 is reducible over ℚ(w) ⇒ [Abel’s Theorem. Let F be a field of characteristic 0, let p be a prime number, and a ∈ F. If xp -a is reducible over F, then it has a linear factor x -c in F[x].] ∃b∈ ℚ(w): b = $\sqrt[5]{7}$. However, x5 -7 is irreducible over ℚ ⇒ [ℚ($\sqrt[5]{7})$: ℚ] ≥ 5, but [ℚ($\sqrt[5]{7})$: ℚ] ≤Since b ∈ ℚ(w) [ℚ(w) : ℚ] = 4⊥
The roots of x5 -7 in ℂ are α, αw, αw2, αw3, αw4, where α = $\sqrt[5]{7}$ and w = $e^{\frac{2πi}{5}}$. The Galois group consist of σp, q: α → αwp, w → wq, 0 ≤ p, q ≤ 4, σ0,1 = id.
σp,q∘σr,s(α) = σp,q(αwr) = σp,q(α)(σp,q(w))r = αwpwqr = αwp+qr. σp,q∘σr,s(w) = σp,q(ws) = wqs. Therefore, σp,q∘σr,s = σp+qr,qs where the addition and multiplication p+qr,qs is in mod 5 ⇒ σ1,12 = σ2, 1. More generally, σ1, 1p = σp, 1. Similarly, σ0, 22 = σ0, 22, and in general, σ0, 2q = σ0, 2q, and σp, 1σ0, 2q = σp, 2q.
The Galois group is generated by β = σ1, 1 and γ = σ0, 2 with presentation ⟨β, γ| β5 = γ4 = β2γβ-1γ-1 = id⟩