Factorization of Polynomials

“How are you doing pal?” “Sucking air, pumping blood, and slowly maintaining an undignified, insignificant existence while pretending but fooling nobody, to overcome a life of suppressed rage, unknown biases, dark areas, emotional rollercoaster, and most importantly, blatant denial,” Apocalypse, Anawim, #justtothepoint.

Recall. A unit or invertible element of a ring R is an element u ∈ R which has an inverse u^-1 ∈ R, so that uu^-1 = u^-1u = 1. An integral domain is a nontrivial commutative ring in which the product of any two nonzero elements is nonzero.

Definition. Let D be an integral domain. An irreducible polynomial is, roughly speaking, a polynomial that cannot be factored into the product of two non-constant polynomials. A non-zero and non-unit polynomial f(x) ∈ D[x] is said to be irreducible if it cannot be written or expressed as the product of two non-units. In other words, whenever f(x) is expressed as a product of two polynomials g(x)h(x) with g(x) and h(x) ∈ D[x], then either g(x) or h(x) is a unit in D[x].

A non-constant polynomial f(x) ∈ F[x], F field, is said to be irreducible if f(x) cannot be expressed a as a product of two polynomials g(x), h(x) ∈ F[x] of lower degree, that is, f(x) = g(x)h(x), deg(g(x)) < deg(f(x)) and deg(h(x)) < deg(f(x)).

Examples

• x²-1 ∈ ℚ[x] is reducible: x² -1 = (x-1)(x +1) where deg(x²-1) = 2, deg(x -1) = deg(x +1) = 1. x²-5x +6 ∈ ℚ[x] is reducible, x²-5x +6 = (x-2)(x-3).
• 2x² + 4 is irreducible over ℚ[x], but reducible over ℤ[x] because 2x² + 4 = 2(x² + 2). 2 is a unit in ℚ[x] (it has inverse 1/2) but not in ℤ[x]. It is also reducible over ℂ, 2x² + 4 = $2(x+i\sqrt{2})(x-i\sqrt{2}).$

  ℂ is algebraically closed, so all polynomials factors into linear terms.

• x² - 2, x² -3 are irreducibles in ℚ[x], but reducibles in ℝ[x], since x² - 2 = $(x-\sqrt{2})(x+\sqrt{2})$ and x² - 3 = $(x-\sqrt{3})(x+\sqrt{3})$
• x² + 1 is irreducible in ℚ[x] or ℝ[x], but reducible in ℂ[x] because x² + 1 = (x - i)(x + i).

Reducibility test for polynomials with degrees two or three. Let F be a field. If f(x) ∈ F[x] and deg(f(x)) = 2 or 3, then f(x) is reducible over F iff f has a zero in F or f(x) is irreducible over F iff f(α) ≠ 0 ∀α ∈ F.

Proof.

⇒) Suppose that f(x) is reducible ⇒∃g(x), h(x) ∈ F[x] such that f(x) = g(x)h(x). Since deg(f(x)) = deg(g(x)) + deg(h(x)) = 2 or 3 ⇒ At least one of g(x) and h(x) has degree 1 (2 = 1 + 1, 3 = 1 + 2). Without losing generality, we can assume ∃a∈ F, a ≠ 0_F such that g(x) = ax + b and f(x) = h(x)(ax +b) ⇒[a ≠ 0_F] -a^-1b is a zero of both g(x) and f(x).

⇐) Suppose that f has a zero in F, ∃α ∈ F: f(α) = 0 ⇒ [By the Factor theorem, f ∈ F[x], α ∈ F zero or root of f (f(α) = 0) ↭ (x -α)|f(x)] (x -α) is a factor of f(x), and therefore, f(x) is reducible over F ∎

Examples

• x² + 1 is irreducible over ℤ₃[x] (0² + 1 = 1, 1² + 1 = 2, and 2² + 1 = 2), but reducible over ℤ₅[x] because 2 and 3 are roots (2² + 1 = 3² + 1 = 0), and therefore x² + 1 = (x -2)(x -3) in ℤ₅[x].

• In ℤ₂[x], f(x) = x³ +x² + x + 1 is reducible because f(1) = 0, but g(x) = x³ + x + 1 is irreducible because g(1) = g(0) = 1.

• Polynomials of degree larger than 3 may be reducible over a field, even though they do not have zeros, e.g., x⁴ + 2x² + 1 = (x² + 1)² and x⁴ -5x² + 6 = (x² -2)(x² -3) in ℚ[x], but they do not have any zeros in ℚ[x]. In ℤ₂[x], f(x) = x⁷ + x⁵ + x³ + x² + 1 = (x⁴ + x + 1)(x³ + x + 1) is reducible even though f(0) = f(1) = 1.

• f(x) = x³ +3x + 2 ∈ ℤ₅[x] is irreducible because deg(f(x)) = 3, f(α) ≠ 0 ∀α ∈ ℤ₅[x] (Figure 1.b.)  

Motivation

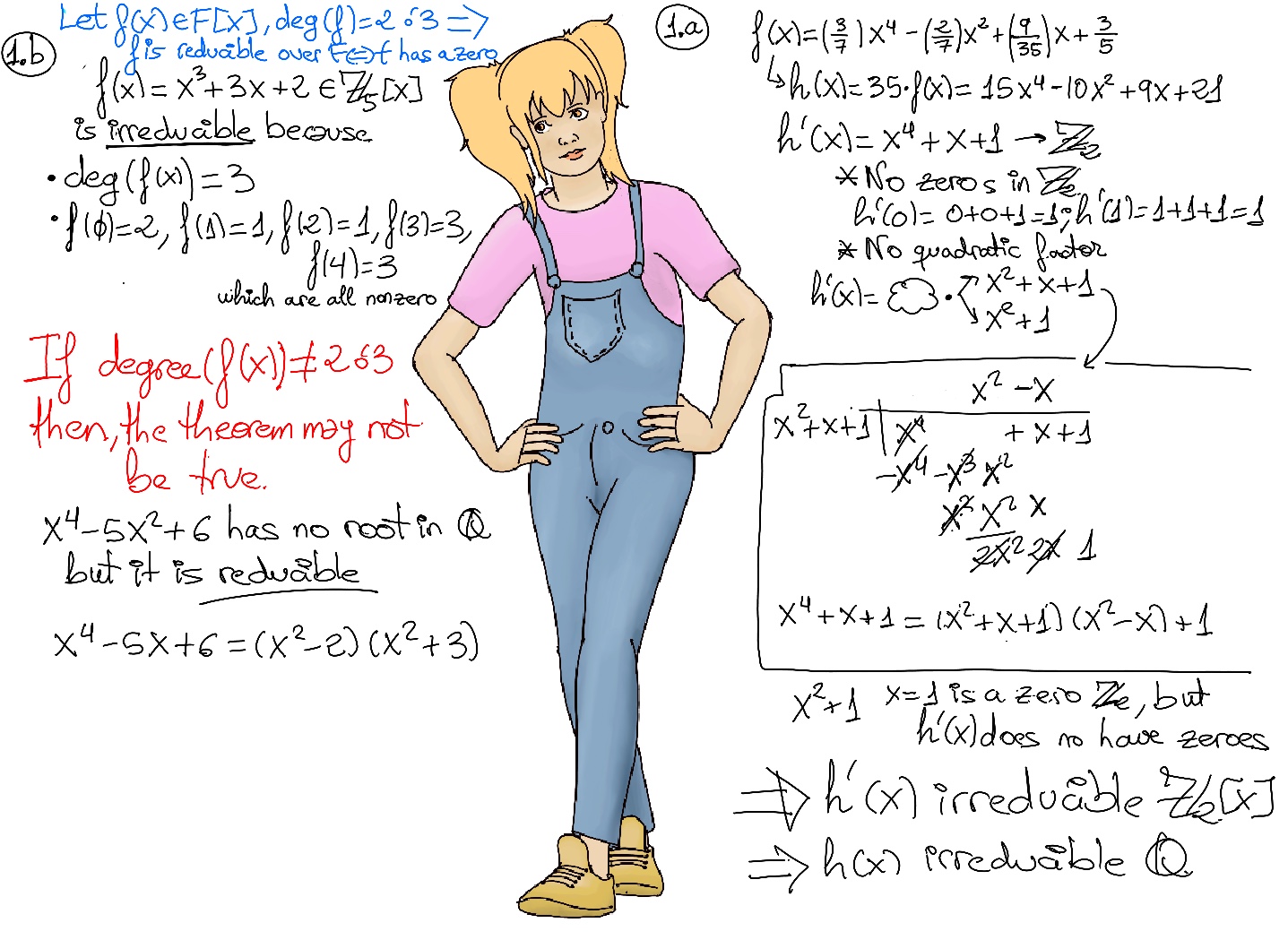
We know that if F is a field, then F[x] is a UFD, a unique factorization domain or factorial ring, that is, an integral domain (a nontrivial commutative ring in which the product of any two non-zero elements is non-zero) in which every non-zero non-unit element can be written as a product of prime or irreducible elements uniquely up to order and units.

An element p of a commutative ring R is said to be prime if it is not the zero element or a unit and whenever p divides ab for some a, b ∈ R ⇒ p divides a or p divides b.

Gauss’ lemma will say that if F is a field of fractions of R, then any polynomial f ∈ R[x] is in the UFD F[x], and so can be written as a product of irreducible factors in an essential unique manner. However, it produces factors of f in Irred(F[x]), but not necessarily in Irred(R[x]), and we only get uniqueness up to associates in F[x], which is a weaker result than uniqueness up to associates in R[x]. It turns out that the way to get around this problem is to consider primitive polynomials.

Definition. Let D be an integral domain. The content of a non-zero polynomial f(x) = a_nxⁿ + a_n-1x^n-1 + ··· + a₀ ∈ D[x] is the greatest common divisor of its coefficients a_n, a_n-1, ··· a₀. A primitive polynomial is an element of D[x] with content equals to 1, that is, gcd(a₀, a₁, ···, a_n) = 1, e.g., 3x² -6x +9 is not primitive, 3x² -6x +10 is primitive.

Gauss’s Lemma. Let D be a unique factorization domain. Let f(x), g(x) ∈ D[x]. Then, the content of f(x)g(x) equals the product of the content of f(x) and the content of g(x). In particular, if f(x), g(x) ∈ D[x] are primitive, then f(x)g(x) is also primitive.

In particular, Gauss’s lemma over the integers states that if f(x) is a polynomial with integer coefficients, then F is called primitive if the greatest common divisor of all its coefficients is 1. If f and g are primitive polynomials over the integers, then their product fg is also primitive.

Proof.

Let f(x) = [We are basically factoring in its content, and everything left behind in f₁ is relatively prime] cf₁(x) and g(x) = dg₁(x) where c and d are the content of f and g, respectively, and f₁ and g₁ are primitive polynomials.

Thus, f(x)g(x) = (cd)f₁(x)g₁(x). Therefore, it suffices to prove Gauss Lemma when f and g are primitive, and as a consequence, the content of fg would be equal to c·d·1. and we would have already proved the theorem for the general case.

Let f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₀ and g(x) = b_mx^m + b_m-1x^m-1 + ··· + b₀. Suppose for the sake of contradiction, there’s a prime, say p, dividing all the coefficients of f(x)g(x). Since f and g are primitives, p does not divide all coefficients of f and g, so let r and s be the smallest integers such that p ɫ a_r and p ɫ b_s.

The coefficient of x^r+s in f(x)g(x) is given as,

c_r+s = $\sum_{i+j=r+s} a_ib_j = a_0b_{r+s}+a_1b_{r+s-1}+···a_rb_s+···+a_{r+s-1}b_1+a_{r+s}b_0$

Since p divides a₀, ···, a_r-1 and b₀, ···, b_s-1 ⇒ p | (c_r+s -a_rb_s) ⇒ [By assumption, p divides all coefficients of f(x)g(x), i.e. p | c_r+s] p | a_rb_s ⇒ [By Euclid’s lemma] p | a_r or p | b_s ⊥ (r and s be the smallest integers such that p ɫ a_r and p ɫ b_s.)

Therefore, the content of f(x)g(x) has no prime divisors in D, that is, the content is a unit.

Corollary. Let D be a UFD and F = Frac(D). Let f(x) ∈ D[x]. If there exists polynomials α, β ∈ F[x] such that f(x) = α(x)·β(x), then there exist polynomials a, b ∈ D[x] such that deg(α) = deg(a), deg(β) = deg(b), and f(x) = e·a(x)·b(x).

Notice that D[x] is in F[x] and f(x) = a(x)b(x) is a D-factorization. In particular, if f(x) ∈ ℤ[x] is reducible over ℚ, then it is reducible over ℤ. Example: f(x) = 2x⁵ + 5x⁴ -8x³ -14x² +6x +9 ∈ ℤ[x], x = 3/2 is a root, therefore f(x) = (x -3/2)(2x⁴ +8x³ + 4x² -8x + 6) = (2x -3)(x⁴ +4x³ + 2x² -4x + 3), and this last one is a factorization over ℤ[x].

Proof:

Suppose that there exist polynomials α, β ∈ F[x] such that f(x) = α(x)β(x). Recall. Let D an integral domain ⇒ F the field of quotients of D, S = {(a, b)| a, b ∈ D and b ≠ 0}, (a, b) ~ (c, d) ↭ ad = bc, F = {[(a, b)]: (a, b) ∈ S}.

Let c, d ∈ D such that cα(x), dβ(x) ∈ D[x] where α, β are polynomials over the field of fractions (c and d are the least common multiple between all of the coefficients of the “denominators” of α and β respectively).

Next, we can factor out the greatest common factor of both polynomials, namely cα(x) = c₁a(x), cβ(x) = d₁b(x), where a(x), b(x) ∈ D[x] are primitive polynomials. We can see clearly that deg(a)=deg(α) and deg(b)=deg(β).

(cd)f(x) =[f(x) = α(x)β(x)] cα(x)·dβ(x) = c₁a(x)·d₁b(x) and by Gauss’ Lemma the content of c₁a(x)·d₁b(x) is c₁d₁ (a(x), b(x) ∈ D[x] are primitive) ⇒ the content of (cd)f(x) is c₁d₁ ⇒ cd | c₁d₁ ⇒ say (cd)e = c₁d₁ ⇒ [(cd)f(x) = (cd)ea(x)b(x), By cancellation] f(x) = ea(x)·b(x) is a factorization in D[x] and deg(a)=deg(α) and deg(b)=deg(β) ∎

Theorem. Let R be a unique factorization domain and F its field of fractions. A non-constant polynomial f in R[x] is irreducible in R[x] if and only if it is both irreducible in F[x] and primitive in R[x]. In particular, a non-constant polynomial in Z[x] is irreducible in Z[x] if and only if it is both irreducible in Q[x] and primitive in Z[x].

2x -4 and 3x + 3 are both irreducibles over ℚ, but 2x -4 = 2(x-2), and 3x + 3 = 3(x +1) are valid factorizations over ℤ (2 and 3 are not units in ℤ because 1/2 ∉ ℤ and 1/3 ∉ ℤ), and therefore 2x -4 and 3x + 3 are not irreducibles over ℤ. The problem is that 2x -4 and 3x + 3 are not primitives.

Theorem. D is a unique factorization domain if and only if D[x] is a unique factorization domain. Examples: ℤ is a UFD (fundamental theorem of arithmetic) ⇒ ℤ[x] is a UFD.

Proof.

⇐) D[x] is a UFD. All polynomials factors uniquely as a product of prime polynomials. In particular, the constant polynomials factors uniquely, and the constant polynomials are exactly the elements of the base domain D.

⇒) First, we need to prove the property of factorization. Let D be a UFD, then D is an integral domain and let F be its field of fractions. We know that F[x] is a Euclidean Domain, hence a PID, hence a UFD.

∀p(x) ∈ D[x], let’s view it inside F[x] ⇒ We can factor p(x), p(x) = f₁(x)··· f_n(x) with f_i(x) ∈ F[x] irreducible.

Let’s take a_i ∈ D such that a_if_i(x) ∈ D[x] (basically we “clear” the denominators by multiplying these polynomials by their corresponding least common multiples of their denominators).

Next, we take b_i ∈ D such that a_if_i(x) = b_ig_i(x) where g_i(x) ∈ D[x] are all both primitives (in a similar fashion as before by factoring out the greatest common factors of these polynomials coefficients) and irreducibles (f_i is irreducible and g_i is primitive ⇒ g_i is irreducible).

A non-constant polynomial f in R[x] is irreducible in R[x] if and only if it is both irreducible in F[x] and primitive in R[x]. a_if_i(x) = b_ig_i(x) where g_i(x) ∈ D[x] are primitives, f_i(x) ∈ F[x] irreducibles ⇒ g_i(x) ∈ D[x] are irreducibles.

a₁···a_np(x) = a₁f₁(x)···a_nf_n(x) = b₁g₁(x)···b_ng_n(x) = b₁···b_ng₁(x)···g_n(x) where g₁(x)···g_n(x) is primitive (g₁(x), g₂(x),···, g_n(x) are all primitives)

Set a = a₁···a_n, b = b₁···b_n, ap(x) = bg₁(x)···g_n(x) ⇒[g₁(x)···g_n(x) is primitive] a | b ⇒ ∃c ∈ D: b = ac ⇒ ap(x) = acg₁(x)···g_n(x) ⇒[By cancellation law, D is an integral domain] p(x) = cg₁(x)···g_n(x) ⇒ [D is a UFD, c ∈ D] p(x) = c₁···c_mg₁(x)···g_n(x) where g_i(x) ∈ D[x] are irreducibles.

It is left to the reader to prove the uniqueness of this factorization.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.