Abacus

An abacus, also called a counting frame, is a mechanical device for performing simple mathematical operations.

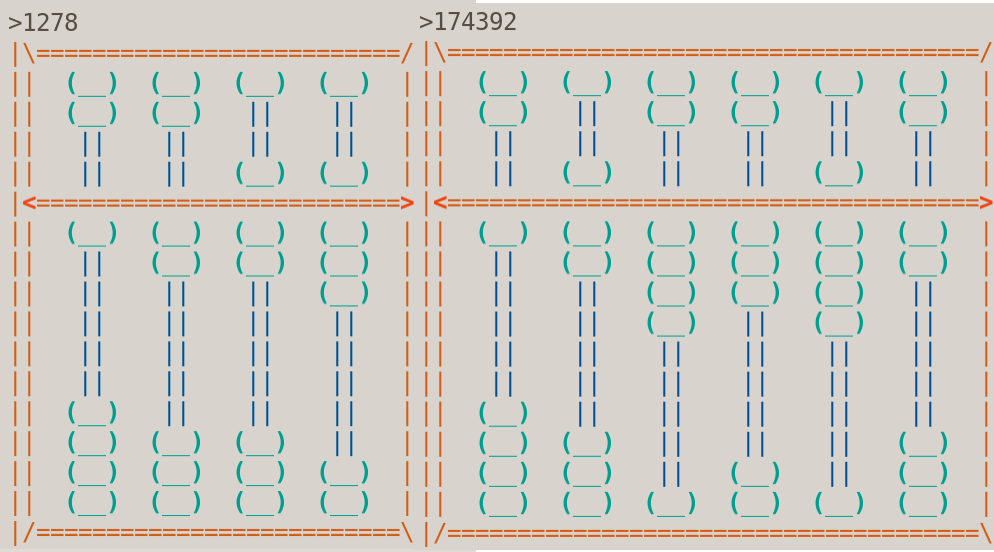
The typical abacus has two decks. Each deck, separated by a beam, has several rods on which are mounted beads. It has 2 beads on the upper deck and 5 on the lower deck. The lower beads are called “Earthly beads” and are each worth one in the first column. They represent a single unit for the rod or pole (1 for the ones pole, 10 for the tens pole, 100 for the hundreds pole, etc.)

The upper beads are called"Heavenly beads" and are worth five in the first column. Each bead in the upper position represents 5 units for the pole (5 for the ones pole, 50 for the tens pole, 500 for the hundreds pole, etc.)

Our end result

Let’s create a Python script that represent numbers on an abacus (code abacus.py).

from rich import print
# This code is inspired by @Nayuki, codegolf.stackexchange.com.
bead = "[bright_red] (__) [/bright_red]"
pole = "[sandy_brown]  ||  [/sandy_brown]"

templateHeader = "[blue]|\\%s/|[/blue]\n"
templateFooter = "[blue]|/%s\\|[/blue]\n"
template = "[blue]|| %s ||[/blue]\\n"
templateTransverseRod = "[blue]|<%s>|[/blue]\\n"

def addSymbol(condition):
    return bead if condition else pole

def abacusAux(digits):
    board = ['', '', '', '', '', '', '', '', '', '', '', '', '']

    for d in digits: # It loops over the digits of the number
        earthDigit = d % 5
        # Let's start with the heavenly beads. To show the numbers zero, one,... four, the heavenly beads are up in heaven. The numbers six, seven... nine are represented by moving the second heaven bead (worth 5) downward towards the crossbar. 
        board[0] += addSymbol(d < 5) # It draws a bead if d < 5, otherwise it draws a pole.
        board[1] += addSymbol(d > 4) # It is the opposite of the previous line. It draws a pole if d < 5, otherwise it draws a bead.
        
        |\\====================/| (*a)
        ||  (__)  (__)  (__)  || (*b) 
        ||   ||   (__)  (__)  || (*c) 734
        ||   ||    ||    ||   || (*d)
        ||  (__)   ||    ||   || (*e)
        
        for i in range(5):
            board[2+i] += addSymbol(earthDigit > i)
            board[7+i] += addSymbol(earthDigit <= i)

Let's represent 4567812390, earthDigit = d % 5 = 4012312340. The first line is (*f).

     
        4     5     6     7     8     1     2      3     9     0
   |<==============================================================>| 
   ||  (__)   ||   (__)  (__)  (__)  (__)  (__)  (__)  (__)   ||   ||

(i=0) The 1st row has a bead for all digits except 0 and 5. Observe that 0 % 5 <= 0 and 5 % 5 <= 0.

 
   ||  (__)   ||    ||   (__)  (__)   ||   (__)  (__)  (__)   ||   ||

(i=1) The 2nd row has a bead for digits 2, 3, 4, 7, 8, and 9. 1 and 6 are excluded because 1 % 5 <= 1 and 6 % 5 <= 1.

 
   ||  (__)   ||    ||    ||   (__)   ||    ||   (__)  (__)   ||   ||

(i=2) The 3rd row has a bead for digits 3, 4, 8, and 9. 2 % 5 <= 2 and 7 % 5 <= 2.

 
   ||  (__)   ||    ||    ||    ||    ||    ||    ||   (__)   ||   ||

(i=3) The 4rd row has a bead for digits 4 and 9. 3 % 5 <= 3 and 8 % 5 <= 3.

 
   ||   ||    ||    ||    ||    ||    ||    ||    ||    ||    ||   ||

(i=4) The 5th row has a pole for all digits. 4 % 5 <= 4 and 9 % 5 <= 4.

 
   ||   ||   (__)   ||    ||    ||    ||    ||    ||    ||   (__)  ||

(i=0) The 6th row has a pole for all digits except 0 (0 % 5 <= 0) and 5 (5 % 5 <= 0).

 
   ||   ||   (__)  (__)   ||    ||   (__)   ||    ||    ||   (__)  ||

(i=1) The 7th row has a pole for digits 2, 3, 4, 7, 8, 9. 1 % 5 <= 1 and 6 % 5 <= 1.

 
   ||   ||   (__)  (__)  (__)   ||   (__)  (__)   ||    ||   (__)  ||

(i=2) The 8th row has a pole for digits 3, 4, 8, and 9. 2 % 5 <= 2 and 7 % 5 <= 2.

 
   ||   ||   (__)  (__)  (__)  (__)  (__)  (__)  (__)   ||   (__)  ||

(i=3) The 9th row has a pole for digits 4 and 9. 3 % 5 <= 3 and 8 % 5 <= 3.

 
   ||  (__)  (__)  (__)  (__)  (__)  (__)  (__)  (__)  (__)  (__)  ||

(i=4) The 10th row has a bead for all digits. 4 % 5 <= 4 and 9 % 5 <= 4.

 
   |/==============================================================\\|
    for i in range(12):
        board[i] = template % "".join(board[i])
    return board

def abacus(number):
    digits = [int(d) for d in number] # It returns a list with the digits of number, e.g., number = '1278', digits = [1, 2, 7, 8]
    count = len(digits) # count is the number of digits.
    board = abacusAux(digits)
    equalsigns = "=" * (count * 6 + 2)
    output = ""
    output += templateHeader % "".join(equalsigns) # It draws (*a)
    output += template % (bead * count) # (*b)
    output += board[0] (*c)
    output += template % (pole * count) (*d)
    output += board[1] (*e)
    output += templateTransverseRod % "".join(equalsigns) (*f)
    for i in range(5):
        output += board[2+i]
    for i in range(5):
        output += board[7+i]
    footer = templateFooter % "".join(equalsigns)
    output += footer

    print(output)

Ascii Art

ASCII art is a type of artwork that is created using the 95 printable (from a total of 128) characters defined by the ASCII, the American Standard Code for Information Interchange.

Other ASCII Art can be found in @yuanquing, github.com.

dic = {
    "0": [
        "XX***XX",
        "X**X**X",
        "X**X**X",
        "X**X**X",
        "X**X**X",
        "X**X**X",
        "XX***XX"
    ],
    "1": [
        "XXX*XXX",
        "XX***XX",
        "XXX*XXX",
        "XXX*XXX",
        "XXX*XXX",
        "XXX*XXX",
        "XXX*XXX"
    ],
    "2": [
        "XXX***X",
        "X*XX**X",
        "XXXXX*X",
        "XXXX**X",
        "XXX**XX",
        "XX**XXX",
        "X*****X"
    ],
    "3": [
        "XX***XX",
        "X*XX**X",
        "XXXXXX*",
        "XXX***X",
        "XXXXXX*",
        "X*XX**X",
        "XX***XX"
    ],
    "4": [
        "XXXX**X",
        "XXX***X",
        "XX*X**X",
        "X*XX**X",
        "*******",
        "XXXX**X",
        "XXXX**X"
    ],
    "5": [
        "*****XX",
        "**XXXXX",
        "****XXX",
        "XXX*XXX",
        "XXXX*XX",
        "*XX*XXX",
        "***XXXX"
    ],
    "6": [
        "XX***XX",
        "X**XXXX",
        "X***XXX",
        "X*XX*XX",
        "X*XXX*X",
        "X*XX*XX",
        "XX**XXX"
    ],
    "7": [
        "XX****X",
        "XXXXX**",
        "XXXXX**",
        "XXXX**X",
        "XXX**XX",
        "XX**XXX",
        "X**XXXX"
    ],
    "8": [
        "X*****X",
        "**XXX**",
        "**XXX**",
        "X*****X",
        "**XXX**",
        "**XXX**",
        "X*****X"
    ],
    "9": [
        "XX***XX",
        "**XX**X",
        "**XXX**",
        "**XX**X",
        "X****XX",
        "XX**XXX",
        "***XXXX"
    ]
}

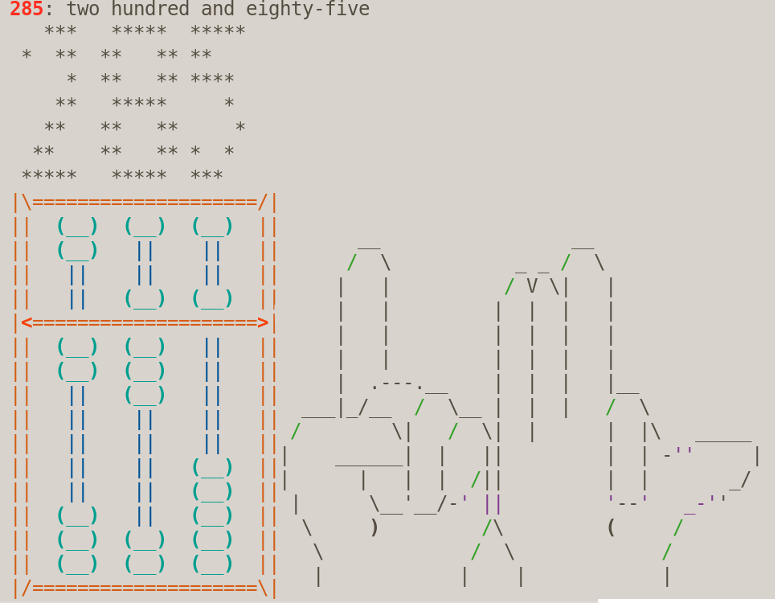
def drawNumber(number):
    """ It draws the number using ASCII Art."""
    for i in range(7): # Each number is drawn using seven lines.
        s = ""
        for j in str(number): # It loops through all its digits.

It replaces X for " “. This is done because each number needs to be drawn with the same number of characters (including empty spaces), i.e., 7 rows x 7 columns, so it will print each and every number, no matter the number of digits, in a consistent and beautiful way.

            print(dic[j][i].replace("X", " "), end=" ")
        print(s)

from fingerbinary import finger_binary
from abacus import abacus, drawNumber
    def show(self):

It shows “number” in a variety of ways. This is a method from the myNumber.

        print(str(self.number) + ": " + num2words(self.number))

num2words is a library that converts numbers like 42 to words like forty-two.

        drawNumber(str(self.number)) # It draws the number using ASCII Art.
        abacus(str(self.number)) # It represents the number on the abacus.
        print(finger_binary(self.number))

It uses the Finger Binary ASCII art generator for Python project. Finger binary is a system for counting and displaying binary numbers on the fingers and thumbs of one or more hands. It is possible to count from 0 to 1023(210−1). You need to download the file fingerbinary.py.

AsciiArt

def drawNumber2(number):
    """ It draws the number using ASCII Art."""
    for i in range(7): # Each number is drawn using seven lines.
        s = ""
        for j in str(number): # It loops through all its digits.
            # It replaces X for " ". This is done because **each number needs to be drawn with the same number of characters (including empty spaces)**, i.e., 7 rows x 7 columns, so it will print each and every number, no matter the number of digits, in a consistent and beautiful way. 
            print(dic[j][i].replace("X", " ").replace("*", str(j)), end=" ")
        print(s)

285: two hundred and eighty-five
   222   88888  55555   
 2  22  88   88 55      
     2  88   88 5555    
    22   88888     5    
   22   88   88     5   
  22    88   88 5  5    
 22222   88888  555  

    @classmethod
    def from_input(cls):
    """ It creates objects of the myNumber class from the user input."""
        while True:
            inputNumber = str(input('Introduce a number: '))
            inputBase = int(input('Introduce a base: '))
            try:
                object = cls(inputNumber, inputBase)
            except ValueError as e:
                print(e)
                continue
            except TypeError as e:
                print(e)
                continue
            if object is not None:
                break
        return object

Set of numbers

What is a set? It is a collection of things or objects, such as animals, plants, vowels (a, e, i, o, u), swearwords, etc. Yes, you’ve guessed it, I am not going to give examples of these pesky words! Basically, it is a list or a group of unordered items which means: The order is irrelevant, {1, 2} is the same set as {2, 1}; and the elements are not repeated.

class myNumber:
    [...]
    # Sets need two methods to make an object hashable: __hash__ and __eq__
    def __eq__(self, other):
        return self.number == other.number
    
    # It returns a unique identifier for the object. It is an integer number representing the value of the object.     
    def __hash__(self):
        return hash(self.number)
    
def main():
    myFirstNumber = myNumber("101", 2)
    print("The hash is: %d" % hash(myFirstNumber))  # >>> The hash is: 5
    mySecondNumber = myNumber("12", 8)
    my_set = set()
    my_set.add(myFirstNumber)
    my_set.add(mySecondNumber)
    my_set.add(myNumber("5"))
    print(my_set)  # >>> {10, 5}

The number of elements that make up or are contained in a set is called the cardinality. The cardinality of my_set is two.

    print("The cardinality of " + str(my_set) + " is: " + str(len(my_set))) # >>> The cardinality of {10, 5} is: 2
    print(myNumber("5") in my_set) # It returns True because 5 is in my_set.
    print(myNumber("9") in my_set) # It returns False because 9 is not in my_set.

Set Operations

The intersection A ∩ B of two sets A and B is a new set containing all the elements common to both sets. Formally, mySet ∩ yourSet = {element: element ∈ mySet and element ∈ yourSet}. set1.intersection(set2) and set1 & set2 both return the set of elements common to both set1 and set2.

    print(my_set & {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")}) # >>> {10}

The union A ∪ B of two sets A and B is a new set containing all the elements of A plus all the elements of B and nothing else. Formally, mySet ∪ yourSet = {element: element ∈ mySet or element ∈ yourSet}. set1.union(set2) and set1 | set2 both return the set of elements in either set1 or set2.

    print(my_set | {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")}) # >>> {2, 4, 5, 6, 8, 10, 12}

The difference A - B between two sets A and B is the set containing all the elements that are in the first set, but not in the second one. We can formulate it as: mySet - otherSet = {element: element ∈ mySet and element ∉ otherSet}. set1.difference(set2) and set1 - set2 both return the set of elements that are in set1 but not in set2.

    print(my_set - {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")}) # >>> {5}

The symmetric difference A △ B of two sets A and B is the set containing all the elements that are in either of the sets, but not in both sets. Strictly speaking: A △ B = { element: (element ∈ A ∧ element ∉ B) or (element ∉ A ∧ element ∈ B) }. set1.symmetric_difference(set2) and set1 ^ set2 both return the set of elements in either set1 or set2 but not in both.

     print(my_set ^ {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")}) # >>> {2, 4, 5, 6, 8, 12}

If the intersection of two sets is empty (A ∩ B = ∅), the sets are said to be disjoint because they do not have any common members or elements.

    print(my_set.isdisjoint({myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")})) # It returns False because {10, 5} and {2, 4, 6, 8, 10, 12} are not disjoint -they share the element 10!

    print(my_set.issubset({myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")})) # It returns False because {10, 5} is not a subset of {2, 4, 6, 8, 10, 12}. 

    my_other = {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")} # my_other = {2, 4, 6, 8, 10, 12}.

    my_other.add(myNumber("5")) # my_other = {2, 4, 5, 6, 8, 10, 12}. We can add (my_set.add(element)) and remove (my_set.remove(element) elements to and from a set. The last one raises an exception if element is not in my_set.

    print(my_set.issubset(my_other)) # It returns True because {10, 5} is not a subset of {2, 4, 5, 6, 8, 10, 12}.

    print(my_other.pop()) # It returns 2 because the method pop() removes a random element from a set and returns it.
    print(my_other) # {4, 5, 6, 8, 10, 12}

    print(my_other.clear()) # It returns None because the method clear() removes all elements from a set. 
    cartesian_product = [(a, b) for a in my_set for b in {myNumber("2"), myNumber("4"), myNumber("6"), myNumber("8"), myNumber("10"), myNumber("12")}]

    print(cartesian_product) # It returns the cartesian product of both sets: [(10, 2), (10, 4), (10, 6), (10, 8), (10, 10), (10, 12), (5, 2), (5, 4), (5, 6), (5, 8), (5, 10), (5, 12)]
if __name__ == '__main__':
    main()

Abacus, Ascii Art, Set of numbers

Abacus

Ascii Art

Set of numbers

Set Operations

Related Posts