Logarithm functions

You have to be Odd, to be number one. Copy from one, it’s plagiarism; copy from three or more, it’s research.

American actress Ilka Chase enjoyed success as a novelist. In one encounter, an anonymous actress said to her: “I enjoyed reading your book. Who wrote it for you?” …to which Chase replied: “Darling, I’m so glad that you liked it. Who read it to you?”

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element x in a set D, x ∈ D (called the domain) exactly one element y in a set E, y ∈ E (called the codomain or range).

• The pair (x, y) is denoted as y = f(x) where: x is the independent variable (input) and y is the dependent variable (output). Often, both the domain D and codomain E are the set of real numbers ℝ or subsets of ℝ. A mathematical function can be thought of as a black box (or machine) that takes an input from its domain and produces exactly one output in its codomain. Inside the machine lives a specific rule (formula, procedure, or mapping) that dictates or tells you which output corresponds to each input, and a key property is uniqueness —each input maps to a single, deterministic output. No input can ever produce two different results (Figure E). The function f(x) = x² accepts any real number x (domain: ℝ) and returns exactly one non-negative value x² (output in codomain: [0,∞)). The input 3 always yields 9, never any other value.

• D is the domain, the set of all possible inputs. E is the codomain or range, the set of all possible outputs.

• Key property💡: Each input has exactly one output. (No input is assigned two different outputs — this is the vertical line test!)

• Examples: constant, f(x) = c, horizontal line, slope = 0; linear, f(x) = mx + b, straight line, constant slope m and y-intercept b; quadratic $f(x) = ax^2 + bx + c$, u-shaped or inverted U, opens up (a > 0) or down (a < 0), vertex at x = $\frac{-b}{2a}$, symmetry about vertical axis through vertex; polynomial, $f(x) = a_n x^n + \dots + a_0$, a smooth and continuous curve, n roots (counting multiplicity), end behaviour determined by its leading term $a_n x^n$; exponential function, $f(x) = a \cdot b^x, a \ne 0, b \gt 0$, rapid growth (b > 1) or decay (0 < b < 1); trigonometric functions, $\sin(x), \cos(x), \tan (z)$ oscillatory, periodic behavior (period 2π for sin/cos, π for tan), sin and cos are bounded between -1 and 1, but tan is unbounded; step function $f(x) = \lfloor x \rfloor$, greatest integer ≤ x, constant on intervals [n, n+1), jumps at integers, its graph is a staircase shape; absolute value f(x) = |x|, V-shaped graph, slope changes at 0.

• Functions can be expressed in multiple forms, each useful in different contexts: verbal description, table of values (list of pairs), algebraic formula, graph, piecewise definition, recursive definition, parametric or integral form, and series representation.

• Evaluating a function means finding or computing the output value f(x) for a given input value x. f(x) = $x^2-2x +4, f(2) = 2^2 -2\cdot 2 + 4 = 4 - 4 + 4 = 4, f(0) = 0^2 -2\cdot 0 + 4 = 4, f(1) = 1^2 -2\cdot 1 + 4 = 1 -2 +4 = 3$

• The x-intercept is any point on the graph that intersects or crosses the x-axis. In other words, it is the value of x when the function (y-coordinate or y-value) is zero. The y-intercept is the point where the graph intersects or crosses the y-axis. y-coordinate of the point whose x-coordinate is 0, e.g., 2x - 3y = 6. x-intercept: set y = 0 → 2x = 6 ⇒ x=3, so (3, 0). y-intercept: set x = 0 → −3y = 6 ⇒ y = −2, so (0, −2).

• f is said to have a local or relative maximum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≥ f(x) $∀ x \in (a, b) ∩ D$. f is said to have a local or relative minimum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≤ f(x) $∀ x \in (a, b) ∩ D$.💡Local extrema can only occur where the function stops rising or falling —either because the derivative is zero, the derivative doesn't exist, or you're at the edge of the domain.

• First Derivative Test. Let f be differentiable on an open interval containing c, except possibly at c itself, and let c be a critical point (so f′(c) = 0 or f′ is undefined). Then:

1. If f′(x) > 0 for x just to the left of c and f′(x) < 0 for x just to the right of c, then f(c) is a local maximum.
2. If f′(x) < 0 for x just to the left of c and f′(x) > 0 for x just to the right of c, then f(c) is a local minimum.
3. If f′(x) does not change sign at c (stays positive or stays negative), then f(c) is not a local extremum.

• Second Derivative Test. If the first derivate of a function at a point c is zero (f'(c) = 0) and the second derivate at this point exists, then: (i) If f''(c) > 0, then f(c) is a local minimum. (ii) If f''(c) < 0, then f(c) is a local maximum. (iii) If f''(c) = 0, the test is inconclusive.
• Vertical asymptotes are vertical lines (perpendicular to the x-axis) of the form x = a (where a is a constant) near which the function grows without bound when x approaches a from at least one side. The line x = a is a vertical asymptote of f if at least one of the one-sided limits is infinite: $\lim_{x \to a^{-}}f(x)=\pm\infty$ or $\lim_{x \to a^{+}}f(x)=\pm\infty$.
• Horizontal asymptotes are horizontal lines (y = c, parallel to the x-axis) that the graph of the function approaches as x grows very large (positively or negatively). In other words, the function values get arbitrarily close to c as long as x is sufficiently large or more formally: $\lim_{x \to \infty}f(x)=c$ and/or $\lim_{x \to -\infty}f(x)=c$.
• A line y = m+b is an oblique (slant) asymptote as $x \to \infty$ if $\lim_{x\to\infty} [f(x) - (mx+b)] = 0.$ This means that the curve of f(x) gets more and more closer to the line y = mx + b as x grows large. For an asymptote y = mx + b as $x \to \infty, m = \lim_{x\to\infty} \frac{f(x)}{x}, b = \lim_{x\to\infty} \bigl(f(x) - m x\bigr)$, provided both limits exist.

Definition. An exponential function is a mathematical function of the form f(x) = b·a^x, where the independent variable is the exponent, and a and b ($b\neq 0$, we want only nontrivial functions) are constants. a is called the base of the function and it should be a positive real number (a > 0).

For a = 1, we could treat it separately as a degenerate exponential, which is just the constant function f(x) = b. We normally want “exponential” to mean “genuinely growing or decaying” rather than just a constant function.

Examples are 2^x, 7^x, and (¹⁄₄)^x. There are three kinds of exponential functions depending on whether a > 1, a = 1, or 0 < a < 1 -Figure 1.a.- The more important example is the natural exponential function, f(x) = e^x where e is the Eulers Number, a mathematical constant approximately equal to 2.71828.

$\frac{d}{dx}e^x=e^x$ It’s the unique (up to scaling) function equal to its own derivative. $e=\lim _{n\rightarrow \infty }\left( 1+\frac{1}{n}\right) ^n$. Furthermore, $a^x=e^{x\ln (a)}$, so every exponential function is just a rescaled version of e^x.

1. Case a > 1. It can be observed that as the exponent increases, the curve get steeper. As x increases, f(x) heads to infinity, $\lim_{x \to ∞} a^x = ∞$. As x decreases, f(x) heads to zero, $\lim_{x \to -∞} a^x = 0$. It is strictly increasing ((e^x)’ = e^x > 0, (a^x)’ = a^x·ln(a) > 0) and has a horizontal asymptote along the x-axis.

   It is important to realize that as x approaches negative infinity, the results become very small but never actually attain zero, e.g., 2^-5 ≈ 0.03125, 2^-15 ≈ 0.00003052. Besides, the base of an exponential function determines the rate of growth or decay. For a > 1, the larger the base, the faster the function grows (Figure iii).

    
2. Case 0 < a < 1. As x increases, f(x) heads to zero, $\lim_{x \to ∞} a^x = 0$. As x decreases, f(x) heads to ∞, $\lim_{x \to -∞} a^x = ∞$. It is strictly decreasing and has a horizontal asymptote along the x-axis. $a^x=\left( \frac{1}{b}\right) ^x=b^{-x}, \text{ where } b = \frac{1}{a}>1$, decay is just growth reflected in the y-axis.
3. When a = 1, the graph is a horizontal line, y = 1. This is technically an exponential function, but it doesn’t model growth or decay, so we usually exclude a = 1 when talking about exponential growth/decay.  

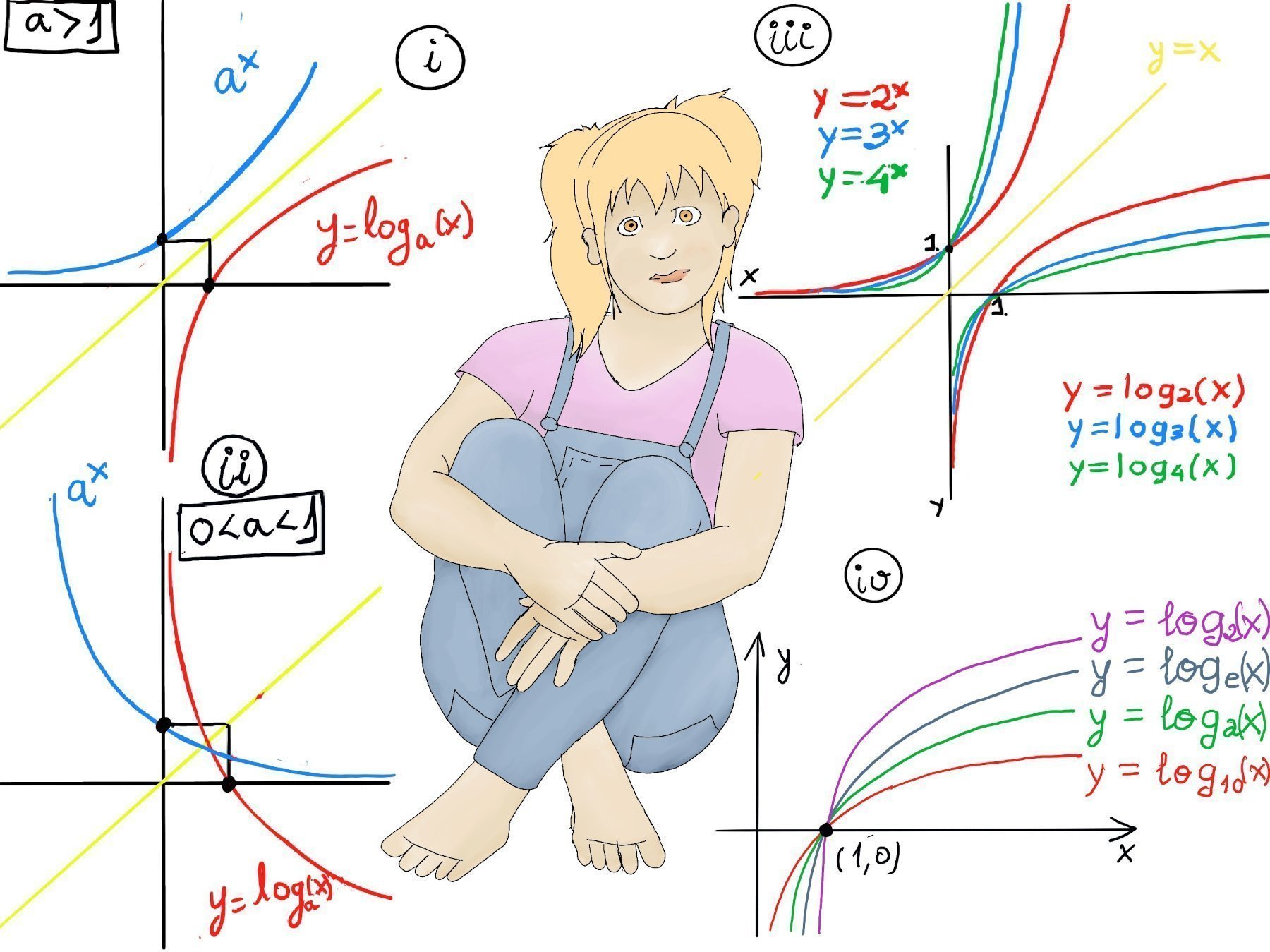
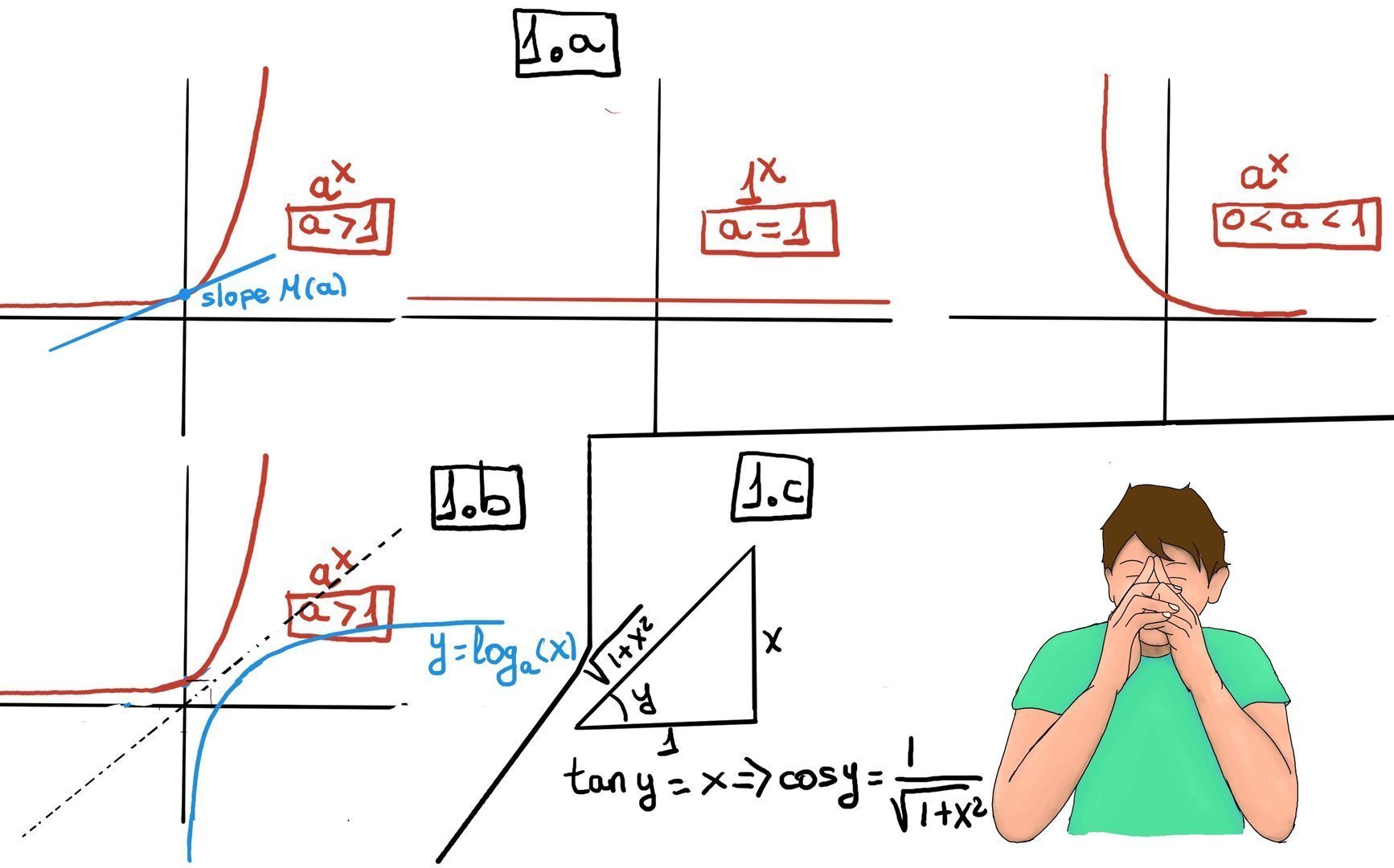
Loosely speaking, the inverse function of a function f is a function that undoes the operation of the original function. If a function f maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted by $f^{-1}$, maps each such element y back to its corresponding x.

Formally, if f(x) = y, then $f^{-1}(y) = x$. This relationship can be summarized by the identities $f^{-1}(f(x)) = x, \forall x \in \mathrm{Dom}(f),$ and $f(f^{-1}(y)) = y, \forall y \in \mathrm{Dom}(f^{-1}).$

Logarithm function

In mathematics, the logarithm is the inverse operation of exponentiation. We call the inverse of a^x the logarithmic function with base a, that is, log_ax = y ↔ a^y = x. In words, the logarithm of a number x to the base a, log_ax, is the exponent to which a must be raised to produce x, e.g., log₄(64) = 3 because 4³ = 64, log₂(16) = 4 because 2⁴ = 16, log₈(512) = 3 because 8³ = 512, but log₂(-3) is undefined in the real numbers (logs require positive arguments).

The logarithm function is a fundamental mathematical tool that serves as the inverse of exponential growth, transforming multiplicative relationships into additive ones. Its applications span virtually every scientific discipline: in finance, logarithms calculate compound interest; in biology, they describe population dynamics and drug elimination from the body; in physics, they quantify radioactive decay and measure earthquake magnitudes. This remarkable versatility makes logarithms essential for solving real-world problems where quantities change at rates proportional to their current values.

Although the base of a logarithm can be any number, the most commonly used bases are 10 and e:

• The logarithm with base e is the natural logarithm. The natural logarithm is the inverse of e^x, that is, ln(x) = y ↔ e^y=x where e is the Eulers Number, a mathematical constant approximately equal to 2.71828.
• The logarithm with base 10 is the common logarithm. $log_{10}(x)$ often written simply log(x) in some contexts (engineering / log tables).

Domain, range, intercepts and asymptotes

• Domain: $(0, \infty)$. The logarithm’s domain consists of real positive numbers.
• Range: $(-\infty,\infty)$. Its range is ℝ.
• x-intercept: (1, 0) because $\log_a(1) = 0$.
• y-intercept: none, logarithm is not defined at x = 0.
• Vertical asymptote. It has a vertical asymptote along the y-axis at x = 0, i.e., the graph “blows up” as $x\to0^+$ (figure i and ii).

Monotonicity and limits

Let a > 0 with $a \neq 1$.

1. If a > 1, e.g. a = 2, e, 10. $\log_a(x)$ is strictly increasing. As x increases, f(x) heads to infinity, $\lim_{x \to ∞} log_a(x) = \infty$. $\lim_{x \to 0+} log_a(x) = -\infty$.

   The bigger the logarithm base, the graph approaches the asymptote x = 0 quicker (Figure iii and iv).

2. If 0 < a < 1, $\log_a(x)$ is strictly decreasing. As x increases, f(x) heads to minus infinity, $\lim_{x \to ∞} log_a(x) = -\infty$. As x decreases, f(x) heads to infinite, $\lim_{x \to 0+} log_a(x) =\infty$.

Basic identities

1. Product Rule. log_a(xy)=log_a(x) + log_a(y).

   Proof: Let $u = \log_a(x), v = \log_a(y)$. Then, $a^{u} = x, a^{v} = y.$ So $xy = a^{u}a^{v} = a^{u+v}$. Taking $\log_a$ gives $\log_a(xy) = u + v = \log_a(x)+\log_a(y)$.

2. Quotient Rule. log_a(^x⁄_y) = log_a(x) - log_a(y).
3. Power Rule. log_a(x^r) = r·log_a(x) ($r \in \mathbb{R}$).
4. Log of 1 and base. log_a(1) = 0 ↭ a⁰ = 1. log_a(a) = 1 ↭ a¹ = a.
5. Change of base formula. $log_b(x)=\frac{log_a(x)}{log_a(b)}$. In particular, $\log_{b}(x) = \frac{\ln(x)}{\ln(b)}$.

   Let y = log_b(x) ↭ b^y = x and z = log_a(x) ↭ a^z = x. Then, z = log_a(x) = $log_a(b^y) = y·log_a(b) ⇒ log_b(x) = y = \frac{z}{log_a(b)} = \frac{log_a(x)}{log_a(b)}$

6. Inversion identities / inverse property. $a^{\log_a(x)} = x, \log_a(a^{t}) = t.$

Differentiation, integration, and series expansion

Derivative of the Natural Logarithm

For x > 0, let y = ln(x) ⇒[By definition] e^y = x ⇒[Differentiating both sides of this equation with respect to x. Recall (e^x)’=e^x] $\frac{d}{dx}(e^y) = \frac{d}{dx}(x) \implies[\text{Applying the chain rule}] e^y\frac{dy}{dx} = 1 \implies[\text{Sove for } \frac{dy}{dx}] \frac{dy}{dx} = \frac{1}{e^y} = \frac{1}{x}.$ Thus, $\boxed{\frac{d}{dx}ln(x) = \frac{1}{x}}, \forall x \gt 0$

Derivative of the Logarithm with Base a

For x > 0, a > 0, and a ≠ 1, let y = log_a(x) ⇒[By definition] a^y = x ⇒ ln(a^y) = ln(x) ⇒[Power Rule. log_a(xⁿ) = n·log_a(x).] y·ln(a) = ln(x) ⇒ y = $\frac{ln(x)}{ln(a)}⇒$[¹⁄_ln(a) is a constant] $\frac{dy}{dx} = \frac{1}{ln(a)}\cdot \frac{1}{x} = \frac{1}{xln(a)}$. Thus, $\boxed{\frac{d}{dx}log_a(x) = \frac{1}{xln(a)}}, \forall x \gt 0$

Integrals and series expansion

• Natural logarithm, $\boxed{\int \ln(x) dx = x\ln(x) - x + C}$. Differentiate xln(x) - x to verify: $\frac{d}{dx}(xln(x) -x) = ln(x) + x\cdot \frac{1}{x} -1 = ln(x).$
• Logarithm with base a (a > 0, $a \ne 1$): $\boxed{\int \log_a(x) dx = \frac{x\ln(x) - x}{\ln(a)} + C}$. $\int \log_a(x) dx = \frac{1}{ln(a)} \int ln(x)dx = \frac{xln(x)-x}{ln(a)} + C$.
• For |t| < 1, the Taylor series of ln(1 + t) about t = 0 is $\boxed{\ln(1+t)=t-\frac{t^2}{2}+\frac{t^3}{3}-\frac{t^4}{4}+\cdots;}$ This gives good approximations for $\ln$ near 1, radius of convergence 1, excluding -1.

For |u| < 1, we have the geometric series: $\frac{1}{1+u} = 1 - u + u^2 -u^3 \cdots$. This is just the usual geometric series applied with x = -u.

$ln(1+t) = \int_{0}^{t} \frac{du}{1+u}$. This follows from these statements:

1. Derivative property: $\frac{d}{dt} \ln(1+t)=\frac{1}{1+t}$ (by the chain rule, since the derivative of ln(x) is 1/x).
2. Initial condition: $\ln(1 + 0) = \ln(1) = 0$.
3. By the Fundamental Theorem of Calculus any function F(t) satisfying $F'(t) = \frac{1}{1+t}$ and F(0) = 0 must be given by the integral $\int_{0}^{t} \frac{du}{1+u}$. Hence, ln(1 + t) is precisely such a function.

Since the geometric series converges uniformly on |u| < 1, we are allowed to integrate term-by-term: $\int_{0}^{t}\frac{du}{1+u} = \int_{0}^{t} (1 - u + u^2 -u^3)du = t-\frac{t^2}{2}+\frac{t^3}{3}-\frac{t^4}{4}+\cdots$

The geometric series converges only for |u| < 1. Since the integration is done over the interval from 0 to t, we need the entire path to stay inside the disk |u| < 1. That requires: |t| < 1. The endpoint t = -1 is excluded because $\ln(1+t)$ has a singularity at t =-1. Thus, the radius of convergence is exactly 1.

Examples:

• f(x) = $ln(\frac{x}{x+1})$

f(x) = $ln(\frac{x}{x+1}) = ln(x)-ln(x+1)$

f’(x) = $\frac{1}{x}-\frac{1}{x+1} = \frac{x+1}{x(x+1)} -\frac{x}{x(x+1)} = \frac{1}{x(x+1)}$

• f(x) = $ln(\frac{x^2·sin(x)}{2x+1})$

f(x) = $ln(\frac{x^2·sin(x)}{2x+1}) = ln(x^2·sin(x))-ln(2x+1) = ln(x^2)+ln(sin(x))-ln(2x+1)= 2ln(x) +ln(sin(x))-ln(2x+1)$

f’(x) = $\frac{2}{x} + \frac{cos(x)}{sin(x)} -\frac{2}{2x+1} = \frac{2}{x} + cot(x) -\frac{2}{2x+1}$

• f(x) = x^x.

y = x^x ⇒ ln(y) = ln(x^x) ⇒ ln(y) = xln(x) ⇒ $\frac{d}{dx} ln(y) = \frac{d}{dx} xln(x) ⇒ \frac{y'}{y} = ln(x)+1 ⇒ y' = y(ln(x)+1) = x^x(ln(x)+1).$

Examples:

• Let’s convert $\log_2(9)$ to base e (natural logarithm), $log_2(9)=\frac{ln(9)}{ln(2)}$= [$ln(9) \approx 2.1972, ln(2) \approx 0.6931$] ≈ 3.1699 ≈ 3.17.

• $log_3(81)=\frac{log_{10}(81)}{log_{10}(3)}$= [$log_{10}(81) \approx 1.9082, log_{10}(3) \approx 0.4771$] ≈ 4.

Solved examples

• Simplify $log_8(\frac{1}{12})+log_8(\frac{12}{5})$

$log_8(\frac{1}{12})+log_8(\frac{12}{5})$ =[Product Rule. log_a(xy)=log_a(x) + log_a(y)] $log_8(\frac{1}{12}·\frac{12}{5}) = log_8(\frac{1}{5}).$

• Solve ln(4x-3) = 7.

ln(4x -3) = 7 ⇒[Apply e^x to both sides] $e^{ln(4x-3)} = e^7 ⇒ 4x -3 = e^7 ⇒ x = \frac{e^7+3}{4}.$

• Solve log₄(x²-2x) = log₄(5x-12).

log₄(x²-2x) = log₄(5x-12) ⇒[a = 4 > 1, logarithm is strictly increasing⇒ one-to-one] x²-2x = 5x-12 ⇒ x² -7x + 12 = 0 ⇒ (x-3)(x-4) = 0 ⇒ x = 3 or 4.

It is essential to make sure to plug these numbers into the original equation so we don’t end up taking logarithms of zero or negative numbers.

log₄(3²-2·3) = log₄(3) = log₄(5·3-12) and log₄(4²-2·4) = log₄(8) = log₄(5·4-12).

• Solve the logarithmic equation $log_3(\sqrt{-7x+1})-7 = -4$

$log_3(\sqrt{-7x+1})-7 = -4$⇒[Isolate the Logarithmic Term] $log_3(\sqrt{-7x+1}) = 3$⇒[Convert to Exponential Form] $3^{log_3(\sqrt{-7x+1})}=3^3 = 27 ⇒ \sqrt{-7x+1} = 27$ ⇒[Square both sides of the equation to solve for x] -7x+1 = 27² = 729 ⇒ -7x = 728 ⇒ $x = \frac{-728}{7}$ = -104.

Besides, $log_3(\sqrt{-7·-104+1})-7 = -4↭log_3(\sqrt{729})-7 = -4 ↭ log_3(27)-7 = -4 ↭ 3-7 = -4$ and obviously $log_3(\sqrt{729})$ is a valid number.

• Solve the logarithmic equation $log_3(2x+1)+log_3(x+8)=3$

$log_3(2x+1)+log_3(x+8)=3$⇒[Product Rule. log_a(xy)=log_a(x) + log_a(y)] $log_3((2x+1)(x+8)) = 3 ⇒$[By definition of logarithms] (2x+1)(x+8) = 3³ = 27.

Expand and rearrange the equation, 2x² +17x +8 = 27. It has two solutions x = -¹⁹⁄₂, x = 1.

It is essential to make sure to plug these numbers into the original equation so we don’t end up taking logarithms of zero or negative numbers.

1. $log_3(2\frac{-19}{2}+1)= log_3(-18)$ ⊥ Since logarithms of negative numbers are undefined, this is not a valid solution.
2. $log_3(2·1+1)+log_3(1+8)=3↭log_3(3)+log_3(9)=3↭1+2=3$, so 1 is a valid solution.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, Andrew Misseldine, blackpenredpen, and MathMajor, YouTube’s channels.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. MIT OpenCourseWare, 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007, YouTube.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.