Linear and Quadratic Approximation

An old joke that Adam told to Even, but makes cents, Once a man said to God “What’s a million years to you?”, and God said “A second.” So the man said to God “What’s a million dollars to you?”, and God said “A penny.” So the man said to God “Would you give me a penny?” And God replied, “Sure, just wait a second.”

Linear and Quadratic Approximations

Linear and quadratic approximations are methods used to approximate a complicated function with simpler, linear or quadratic functions near a specific point. This is useful when algebra becomes messy, the exact value is difficult to calculate, computationally costly, or tedious to find. These approximations are valuable in calculus and numerical analysis for estimating the behavior of functions near certain points, understanding local behaviour, or for simplifying calculations.

When using approximation, you sacrifice some accuracy for the ability to perform complex calculations easily and quickly.

Linear approximation

Linear approximation does a very good job of approximating values of f(x) as long as we stay near x = a, that is, in the neighborhood around a. If a function y = f(x) is differentiable at a point (a, f(a)), the function looks like its tangent line in a small open interval containing a. It allows us to approximate the original function f (it is sometimes computationally too costly -in terms of resources- or algebraically complicated) with a simpler function L that is linear.

The tangent line provides the “best” linear approximation to f at the point a. In other words, zoom in far enough on a smooth curve at x = a, and it becomes indistinguishable from a straight line: the tangent.

The Linear Approximation Formula

For a function f differentiable at $x_0$, the linear approximation of $f$ at $x_0$ is the tangent line: $\boxed{L(x) = f(x_0) + f'(x_0)(x - x_0)}$ (it touches the curve at this particular point $x_0$).

Approximation: $f(x) \approx L(x) \quad \text{for } x \approx x_0$ (for x near $x_0$). This is the first-order Taylor polynomial of $f$ at $x_0$. The closer $x$ is to $x_0$, the better the approximation is (error is generally of order $(x - x_0)^2$).

How to Perform Linear Approximation

1. Choose a base point $x_0$ close to where you want to evaluate (preferably where $f$ is easy to compute).
2. Evaluate the function: compute $f(x_0)$, the function value at the base point.
3. Calculate the derivative $f'(x_0)$ to find the slope of the tangent line at that point.
4. Use the point-slope form to write the equation of the tangent line, $L(x) = f(x_0) + f'(x_0)(x - x_0)$.
5. Use this linear equation to evaluate and estimate the value of the function at points close to x₀, $f(x) \approx L(x) \quad \text{for } x \approx x_0$.

Example: Linearization of $\ln(x)$ at $x_0 = 1$

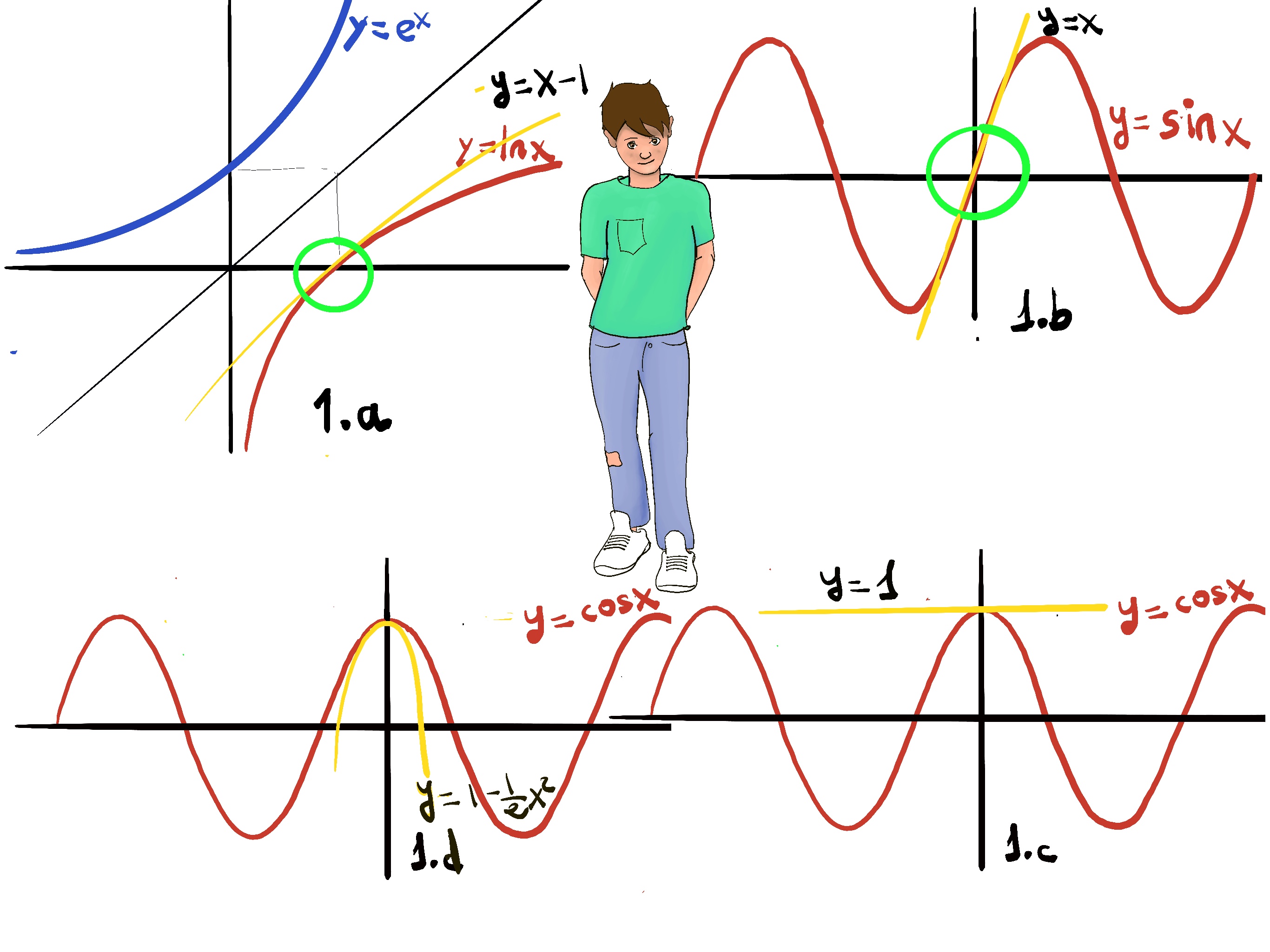
We know $\ln(1) = 0, (\ln x)' = \dfrac{1}{x}$, so $\ln'(1) = 1$. Thus, the linear approximation at $x_0 = 1$ is: $L(x) = \ln(1) + \ln'(1)(x - 1) = 0 + 1(x - 1) = x - 1.$

So for $x$ near 1: $\ln x \approx x - 1.$ (Figure 1.a).

Essential Approximation

Essential Approximation (it is a good idea to memorize these): $\sin x \approx x$, $\cos x \approx 1$, $\tan x \approx x$, $e^x \approx 1 + x$, $\ln(1 + x) \approx x$, $(1 + x)^r \approx 1 + rx$, $\frac{1}{1 + x} \approx 1 - x$, $\frac{1}{1 - x} \approx 1 + x$, $\sqrt{1 + x} \approx 1 + \frac{x}{2}$, $\frac{1}{\sqrt{1 + x}} \approx 1 - \frac{x}{2}$.

Derivation of Key Approximations

1. $\sin x \approx x$, $\sin(0) = 0$. $f'(x) = \cos x, f'(0) = \cos(0) = 1$. Linear approximation: $L(x) = 0 + 1 \cdot (x - 0) = x$, e.g., $\sin(0.1) = 0.0998334... \approx 0.1$
2. $\cos x \approx 1$ near 0 (1.c). $f(x) = \cos x$, $cos(0) = 1$, $f'(x) = -\sin x$, $f'(0) = 0$. $L(x) = 1 + 0(x - 0) = 1$. So $\cos x \approx 1$ for small $x$, e.g., $\cos(0.1) = 0.9950 \approx 1$.
3. $e^x \approx 1 + x$ near 0. $f(x) = e^x$, $f(0) = 1$, $f'(x) = e^x$, $f'(0) = 1$. $L(x) = 1 + x$, so $e^x \approx 1 + x$ for small $x$, e.g., $e^{0.2} = 1.2214 \approx 1.2$.
4. $\ln(1 + x) \approx x$. $f(x) = \ln(1 + x)$, $x_0 = 0$. $\ln(1) = 0$, $f'(x) = \frac{1}{1+x}, f'(0) = 1$. Linear approximation: $L(x) = 0 + 1 \cdot x = x$, e.g., $\ln(1.1) = 0.0953... \approx 0.1$.
5. $(1 + x)^r \approx 1 + rx$. $f(x) = (1 + x)^r$, $x_0 = 0$. $(1 + 0)^r = 1$. $f'(x) = r(1 + x)^{r-1}, f'(0) = r \cdot 1 = r$. Linear approximation: $L(x) = 1 + rx$

Special cases: r = 2, $(1+x)^2 \approx 1 + 2x$; r = 3, $(1+x)^3 \approx 1 + 3x$; $r = \frac{1}{2}$, $\sqrt{1+x} \approx 1 + \frac{x}{2}$; r = -1, $\frac{1}{1+x} \approx 1 - x$; $r = -\frac{1}{2}$, $\frac{1}{\sqrt{1+x}} \approx 1 - \frac{x}{2}$.

Example: $(1.1)^3 = 1.331 \approx 1 + 3(0.1) = 1.3$

• Approximate the number $\sqrt[4]{1.1}$

Let $f(x) = \sqrt[4]{x} = x^{1/4}$. Choose $x_0 = 1$ (near 1.1 and easy to compute).

$1^{1/4} = 1, f'(x) = \frac{1}{4}x^{-3/4}, f'(1) = \frac{1}{4}$. Linear approximation: $L(x) = 1 + \frac{1}{4}(x - 1)$

Evaluate at $x = 1.1$: $\sqrt[4]{1.1} \approx 1 + \frac{1}{4}(0.1) = 1.025$

Actual value: $\sqrt[4]{1.1} = 1.02411...$ Error: $|1.025 - 1.02411| \approx 0.00089$ (less than 0.1%)

• Approximate $\sqrt{4.1}$

Let $f(x) = \sqrt{x}$. Choose $x_0 = 4$ (perfect square near 4.1).

Calculations: $\sqrt{4} = 2, f'(x) = \frac{1}{2\sqrt{x}}, f'(4) = \frac{1}{4}$.

Linear approximation: $L(x) = 2 + \frac{1}{4}(x - 4)$

Evaluate at $x = 4.1$: $\sqrt{4.1} \approx 2 + \frac{1}{4}(0.1) = 2.025 \approx[\text{Actual value}] 2.02485...$

• Find linear approximation near x = 0 of $\frac{e^{-3x}}{\sqrt{1+x}}$

Individual approximations: $e^{-3x} \approx 1 + (-3x) = 1 - 3x, (1+x)^{-1/2} \approx 1 + \left(-\frac{1}{2}\right)x = 1 - \frac{x}{2}$

Combine both individual approximations: $\frac{e^{-3x}}{\sqrt{1+x}} = e^{-3x}(1+x)^{-1/2} \approx (1 - 3x)\left(1 - \frac{x}{2}\right) =[\text{Expand (keeping only linear terms)}]= 1 - \frac{x}{2} - 3x + \frac{3x^2}{2} \approx 1 - \frac{7x}{2}$

We ignore $x^2$ terms (quadratic and higher other terms) since they’re negligible for small $x$.

$\boxed{\frac{e^{-3x}}{\sqrt{1+x}} \approx 1 - \frac{7x}{2}}$

$\frac{e^{-3x}}{\sqrt{1+x}} = e^{-3x}(1+x)^{-1/2} ≅ (1-3x)(1-\frac{1}{2}x) ≅~ 1 -3x -\frac{1}{2}x +\frac{3}{2}x^{2} ≅ 1 -3x -\frac{1}{2}x ≅ 1 -\frac{7}{2}x$. Observe that we do not care about quadratic and higher other terms and consider them as negligible as long as we are close enough to 0.

Application: Evaluating Limits

The linear approximation helps evaluate certain limits intuitively, e.g., $\lim_{x \to 0} \frac{\sin x}{x}$

Since $\sin x \approx x$ for $x$ near 0: $\frac{\sin x}{x} \approx \frac{x}{x} = 1$

This suggests (and is consistent with) $\lim_{x \to 0} \frac{\sin x}{x} = 1$.

Limit	Approximation	Result
$\lim_{x \to 0} \frac{e^x - 1}{x}$	$\frac{(1+x) - 1}{x} = 1$	$1$
$\lim_{x \to 0} \frac{\ln(1+x)}{x}$	$\frac{x}{x} = 1$	$1$
$\lim_{x \to 0} \frac{1 - \cos x}{x}$	$\frac{1 - 1}{x} = 0$	$0$
$\lim_{x \to 0} \frac{\tan x}{x}$	$\frac{x}{x} = 1$	$1$

Quadratic approximation

When using approximation you sacrifice some accuracy for the ability to perform complex calculations easily and fast. Quadratic approximation is used when the linear approximation is not good or close enough, e.g., the linear approximation of $\cos(x)$ near 0 is $L(x) = 1$ — a horizontal line! This doesn’t capture the parabolic shape of cosine at all.

The Quadratic Approximation Formula

For a function $f$ that is twice differentiable at $x_0$, the basic formula for quadratic approximation at $x_0$ is $\boxed{Q(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2}(x - x_0)^2}$

This provides the best-fit parabola to the function at $x_0$ and this is generally enough for $x \approx x_0$.

Ideally, the quadratic approximation of a quadratic function, say $f(x) = a + bx + cx^2$, should be identical to the original function.

At $x_0 = 0$: (i) $f(0) = a$; (ii) $f'(x) = b + 2cx \Rightarrow f'(0) = b$; (iii) $f''(x) = 2c \Rightarrow f''(0) = 2c$.

Solving: $f(0) = a, f'(0) = b, f''(0) = 2c \implies c = \frac{f''(0)}{2}$. So: $f(x) = f(0) + f'(0)x + \frac{f''(0)}{2}x^2$ ✓

How to Perform Quadratic Approximation

1. Choose base point $x_0$.
2. Calculate $f(x_0)$
3. Calculate the first $f'(x_0)$ and second derivatives $f''(x_0)$ at that point.
4. Plug these values into the quadratic approximation formula to get the quadratic polynomial that approximates the function near x₀, $Q(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2}(x-x_0)^2$
5. Use this quadratic polynomial to evaluate and estimate the value of the function at points close to $x_0$.

Standard Quadratic Approximations at $x_0 = 0$

• $\sin x \approx x$
• $\cos x \approx 1 - \frac{x^2}{2}$
• $\tan x \approx x + \frac{x^3}{3} \approx x$ (no $x^2$ term)
• $e^x \approx 1 + x + \frac{x^2}{2}$
• $\ln(1 + x) \approx x - \frac{x^2}{2}$
• $(1 + x)^r \approx 1 + rx + \frac{r(r-1)}{2}x^2$
• $\frac{1}{1 + x} \approx 1 - x + x^2$
• $\frac{1}{1 - x} \approx 1 + x + x^2$
• $\sqrt{1 + x} \approx 1 + \frac{x}{2} - \frac{x^2}{8}$

The linear approximation of cos(x) near 0 is the straight horizontal line y = 1. This doesn’t seem like a very good approximation. The quadratic approximation to the graph of cos(x) is a parabola that opens downward: $\cos(x) \approx 1 - \frac{x^2}{2}$ (1.d.), this is much closer to the shape of cos(x) than the line y = 1.

Derivation of Key Quadratic Approximations

• Find quadratic approximation of $\cos x \approx 1 - \frac{x^2}{2}$

$f(x) = \cos x$; $x_0 = 0, \cos 0 = 1, f'(x) = -\sin x, f'(0) = 0, f''(x) = -\cos x, f''(0) = -1$

Quadratic approximation: $Q(x) = 1 + 0 \cdot x + \frac{-1}{2}x^2 = 1 - \frac{x^2}{2}$.

$\cos(0.5) =[\text{Real value}] 0.87758...$ vs. $1 - \frac{0.25}{2} = 0.875$.

• Find quadratic approximation of $e^x \approx 1 + x + \frac{x^2}{2}$

$f(x) = e^x; x_0 = 0; f(0) = 1, f'(0) = 1, f''(0)= 1$.

Quadratic approximation: $Q(x) = 1 + x + \frac{1}{2}x^2$

$e^{0.5} =[\text{Real value}] 1.6487...$ vs. $1 + 0.5 + 0.125 = 1.625$

• Find quadratic approximations for f(x) = ln(1.1), $\ln(1 + x) \approx x - \frac{x^2}{2}$

$f(x) = \ln(1 + x); x_0 = 0; f(0) = 0, f'(x) = \frac{1}{1+x}, f'(0) = 1, f''(x) = -\frac{1}{(1+x)^2}, f''(0) = -1$

Quadratic approximation: $Q(x) = 0 + x + \frac{-1}{2}x^2 = x - \frac{x^2}{2}$

Let $x = 0.1, \ln(1.1) =[\text{Actual value}] 0.09531... \ln(1 + 0.1) \approx 0.1 - \frac{0.01}{2} = 0.095$

• Find the quadratic approximation of $(1 + x)^r \approx 1 + rx + \frac{r(r-1)}{2}x^2$

$f(x) = (1 + x)^r$, $x_0 = 0; f(0) = 1, f'(x) = r(1+x)^{r-1}, f'(0) = r, f''(x) = r(r-1)(1+x)^{r-2}, f''(0) = r(r-1)$.

Quadratic approximation: $Q(x) = 1 + rx + \frac{r(r-1)}{2}x^2$.

Special case: $r = \frac{1}{2}$ (square root) $\sqrt{1+x} \approx 1 + \frac{x}{2} + \frac{\frac{1}{2}(-\frac{1}{2})}{2}x^2 = 1 + \frac{x}{2} - \frac{x^2}{8}$

• Find the linear and quadratic approximations for f(x) = $\sqrt x$ near x = 4.

f(4) = 2, f’(x) = $\frac{1}{2\sqrt{x}} = \frac{1}{2}·x^{\frac{-1}{2}}, f'(4) = \frac{1}{4}$; f’’(x)= $\frac{1}{2}·\frac{-1}{2}·x^{\frac{-1}{2}-1} = \frac{-1}{4·x^{\frac{3}{2}}} = \frac{-1}{4·x·\sqrt{x}}, f''(4) = -\frac{1}{32}$, then

1. Linear approximation, L(x) = f(4) + f’(4)(x-4) = $2 + \frac{1}{4}(x-4) = 1 + \frac{1}{4}x$.
2. Quadratic approximation, $Q(x) = 2 + \frac{1}{4}(x-4) + \frac{-1/32}{2}(x-4)^2 = 2 + \frac{1}{4}(x-4) - \frac{1}{64}(x-4)^2$

Expanding: $Q(x) = 2 + \frac{x}{4} - 1 - \frac{1}{64}(x^2 - 8x + 16) = 1 + \frac{x}{4} - \frac{x^2}{64} + \frac{x}{8} - \frac{1}{4} = \frac{3}{4} + \frac{3x}{8} - \frac{x^2}{64}$.

$\sqrt{5} =[\text{Actual value}] = 2.2360679... \approx[\text{Linear}] 2.25 \text{ (error ≈ 0.01393) } \approx[\text{Quadratic}] 2.2344...$ (error ≈ 0.00169). The quadratic approximation is indeed much closer because it captures the concavity of the square root function.

• Find quadratic approximations for $f(x) = xe^{-2x}$ near $x = 1$

$x_0 = 1$. Calculate derivatives: $f(x) = xe^{-2x}, f(1) = 1 \cdot e^{-2} = e^{-2}, f'(x) = e^{-2x} + x(-2e^{-2x}) = e^{-2x}(1 - 2x), f'(1) = e^{-2}(1 - 2) = -e^{-2}$.

$f''(x) = -2e^{-2x}(1-2x) + e^{-2x}(-2) = -2e^{-2x}(1-2x+1) = -4e^{-2x}(1-x), f''(1) = -4e^{-2}(0) = 0$

Quadratic approximation: $Q(x) = e^{-2} + (-e^{-2})(x-1) + \frac{0}{2}(x-1)^2 = e^{-2}(1 - (x-1)) = e^{-2}(2 - x)$

Since $f''(1) = 0$, the quadratic approximation equals the linear approximation!

• Quadratic Approximation for $\frac{e^{-3x}}{\sqrt{1+x}}$ near $x = 0$

Individual approximations: $e^{-3x} \approx 1 + (-3x) + \frac{(-3)^2}{2}x^2 = 1 - 3x + \frac{9x^2}{2}$; $(1+x)^{-1/2} \approx 1 + \left(-\frac{1}{2}\right)x + \frac{(-\frac{1}{2})(-\frac{3}{2})}{2}x^2 = 1 - \frac{x}{2} + \frac{3x^2}{8}$

Multiply (keeping terms up to $x^2$): $\left(1 - 3x + \frac{9x^2}{2}\right)\left(1 - \frac{x}{2} + \frac{3x^2}{8}\right)$

Expand systematically:

• Constant term: $1 \cdot 1 = 1$
• Linear terms: $1 \cdot \left(-\frac{x}{2}\right) + (-3x) \cdot 1 = -\frac{x}{2} - 3x = -\frac{7x}{2}$
• Quadratic terms: $1 \cdot \frac{3x^2}{8} + (-3x)\left(-\frac{x}{2}\right) + \frac{9x^2}{2} \cdot 1$ $= \frac{3x^2}{8} + \frac{3x^2}{2} + \frac{9x^2}{2} = \frac{3 + 12 + 36}{8}x^2 = \frac{51x^2}{8}$

Result: $\boxed{\frac{e^{-3x}}{\sqrt{1+x}} \approx 1 - \frac{7x}{2} + \frac{51x^2}{8}}$

Connection to Taylor series

The Taylor series of a function f(x) about a point $x_0$ is given by $f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n$ provided the function is infinitely differentiable at $x_0$ and the series converges to f(x) in some neighborhood of $x_0$. Truncating the series after a finite number of terms yields a polynomial approximation of f.

• L(x) is the 1st-order approximation (terms up to $x^1$).
• Q(x) is the 2nd-order approximation (terms up to $x^2$).
• More terms improve accuracy but increase computational cost.

Terms	Name	Formula
First 1	Constant	$f(x_0)$
First 2	Linear	$f(x_0) + f'(x_0)(x-x_0)$
First 3	Quadratic	$f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2}(x-x_0)^2$
First 4	Cubic	$f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2}(x-x_0)^2 + \frac{f'''(x_0)}{6}(x-x_0)^3$
All	Taylor Series	$\sum_{n=0}^{\infty} \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n$

$x$	$e^x$	$L(x) = 1+x$	$Q(x) = 1+x+\frac{x^2}{2}$	Error L(x)	Error Q(x)
0	1	1	1	0.0000	0.0000
0.1	1.1052	1.1	1.105	0.0052 (0.47%)	0.0002 (0.02%)
0.5	1.6487	1.5	1.625	0.1487 (9.02%)	0.0237 (1.44%)
1	2.7183	2	2.5	0.7183 (26.43%)	0.2183 (8.03%)

The quadratic approximation Q(x) is significantly closer to $e^x$ than the linear L(x), as the $x^2$ term captures the curvature near x = 0.

Interpretation

• Constant approximation: The horizontal line $y = f(x_0)$. Best near $x_0$ if the function is nearly constant.
• Linear approximation: The tangent line at $x_0$. Captures the function’s instantaneous rate of change (slope).
• Quadratic approximation: Includes curvature via the second derivative. Often much more accurate than the linear approximation.
• Cubic and higher: Each additional term generally improves the approximation locally, provided the higher derivatives are well‑behaved.

Full Taylor Series for Common Functions

Function	Series	Radius of Convergence	Key Pattern
$e^x$	$\displaystyle\sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$	$\mathbb{R}$ (all $x$)	All terms positive; rapid growth
$\sin x$	$\displaystyle\sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots$	$\mathbb{R}$	Odd powers only; alternating signs
$\cos x$	$\displaystyle\sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots$	$\mathbb{R}$	Even powers only; alternating signs
$\ln(1+x)$	$\displaystyle\sum_{n=1}^\infty \frac{(-1)^{n+1} x^n}{n} = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots$	$(-1, 1]$	Slow convergence; $x=1$ gives $\ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \cdots$
$(1+x)^r$	$\displaystyle\sum_{n=0}^\infty \binom{r}{n} x^n = 1 + rx + \frac{r(r-1)}{2!}x^2 + \cdots$	$\vert x\vert < 1$	Binomial series; terminates if $r \in \mathbb{N}$
$\frac{1}{1-x}$	$\displaystyle\sum_{n=0}^\infty x^n = 1 + x + x^2 + x^3 + \cdots$	$\vert x \vert < 1$	Geometric series; divergence at $\vert x \vert \geq 1$

1. Analyticity. $e^x, \sin(x), \cos(x)$ are entire (analytic everywhere). Their Taylor series converge for all $x \in \mathbb{C}$.
2. Finite radius. ln(1 + x) and $(1+x)^r$ have radius 1 because of singularities at x = 1. The series cannot “see” past this barrier.
3. Conditional convergence. At the boundary x = 1, ln(1 + x) converges (alternating harmonic series), but $\frac{1}{1-x}$ diverges.
4. Binomial series: $(1+x)^r=\sum _{n=0}^{\infty }{r \choose n}x^n=1+rx+\frac{r(r-1)}{2!}x^2+\cdots $. Interval of convergence: |x| < 1 for general real (or complex) r. If $r\in \mathbb{N}$, the series terminates and becomes a polynomial; otherwise it’s genuinely infinite.
5. Series (geometric): $\frac{1}{1-x}=\sum _{n=0}^{\infty }x^n=1+x+x^2+x^3+\cdots$. Interval of convergence: |x| < 1. Prototype of all power series; divergence at $|x|\geq 1$, with especially educational behavior at x = 1 (harmonic-type blow-up) and x = -1 (oscillation).

$\ln (1+x)=\sum _{n=1}^{\infty }\frac{(-1)^{n+1}x^n}{n}=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots $. Interval of convergence: $-1 \lt x \leq 1$. At x = 1: converges to $\ln(2)$. At x = -1: $\sum (-1)^{n+1}(-1)^n/n = -\sum 1/n$ diverges. Alternating, slowly convergent near x = 1; great for theoretical work, not for fast computations.

Taylor Error Bounds (Lagrange Remainder)

For a function f with n+1 continuous derivatives near $x_0$, the Taylor polynomial of degree n satisfies: $f(x)=T_n(x)+R_n(x)$ where the remainder has the form $R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}$ for some $\xi$ between x and $x_0$.

Taking absolute values and bounding the derivative gives: $|R_n(x)|\leq \frac{M_{n+1}}{(n+1)!}|x-x_0|^{n+1}$, where $M_{n+1}=\max_{t\mathrm{\ between\ }x\mathrm{\ and\ }x_0}|f^{(n+1)}(t)|$.

Linear approximation: (n = 1) Taylor polynomial: $L(x)=f(x_0)+f'(x_0)(x-x_0)$. Linear approximation error: $|f(x)-L(x)|\leq \frac{M_2}{2}|x-x_0|^2$ where $M_2 = \max|f''(t)|$ for $t$ between $x$ and $x_0$.

Quadratic approximation (n = 2): Taylor polynomial: $Q(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2}(x-x_0)^2.$ Quadratic approximation error: $|f(x)-Q(x)|\leq \frac{M_3}{6}|x-x_0|^3$ where $M_3 = \max|f'''(t)|$ for $t$ between $x$ and $x_0$.

They tell us:

• how accurate the approximation is,
• how fast the error shrinks as $x\rightarrow x_0$,
• how smoothness (higher derivatives) controls approximation quality.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.