Derivate of inverse functions

The man who asks a question is a fool for a minute, the man who does not ask is a fool for life, Confucius.

Recall

The derivative of a function at a specific input value describes the instantaneous rate of change. Geometrically, when the derivative exists, it is the slope of the tangent line to the graph of the function at that point. Algebraically, it represents the ratio of the change in the dependent variable to the change in the independent variable as the change approaches zero.

Definition. A function f(x) is differentiable at a point “a” in its domain, if its domain contains an open interval around “a”, and the following limit exists $f'(a) = L = \lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then the following inequality holds |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

Basic important derivatives

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$ (works for any real n).
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Difference Rule: $\frac{d}{dx}(f(x) - g(x)) = f'(x) - g'(x)$
4. Constant Multiple Rule: $\frac{d}{dx}(c \cdot f(x)) = c \cdot f'(x)$ where c is a constant.
5. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f'(x)g(x) + f(x)g'(x)$.
6. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2}$, provided $g(x) \ne 0$.
7. Chain Rule: $\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)$

Derivate of inverse functions

The inverse function of a function f is a function that undoes the operation of the original function. If f maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted as $f^{-1}$, maps each element y back to its corresponding x: $y = f(x) \iff x = f^{-1}(y)$

The Fundamental Property. For a given function f, its inverse f^-1 is a function that reverses its result (f^-1 reverses the input and output of the original function): $f^{-1}(f(x)) = x \quad \text{and} \quad f(f^{-1}(x)) = x$

Existence of Inverse Functions

For an inverse function to exist, the original function must be both one-to-one (injective) and onto (surjective).

• A function $f: A \to B$ is one-to-one if each element of the domain maps to a distinct (unique) element in the codomain (Horizontal Line Test — no horizontal line intersects the graph more than once). If f(a) = f(b), then a = b.
• A function is onto if every element in the codomain has a pre-image in the domain (Range = Codomain). For any $y \in B$, there is always at least one $x \in A$ such that f(x) = y.
• If a function is both injective and onto, then it is bijective. A function has an inverse if and only if it is bijective.

Examples

• Square root and square. Let f(x)=$\sqrt{x}$ with domain x ≥ 0 (1.a.). Then, the inverse is: $f^{-1}(x) = x^2, x \ge 0$ because $f(f^{-1}(x)) = \sqrt{x^2} = x \quad (x \ge 0), f^{-1}(f(x)) = (\sqrt{x})^2 = x.$ The square function (on $[0,\infty)$) is the inverse of the square-root function (on $[0,\infty)$).
• Exponential and logarithm. The natural logarithm function is the inverse of the exponential function: $f(x) = e^x, f^{-1}(x) = \ln(x), x > 0$. More generally, logarithmic functions are the inverses of exponential functions; for $a > 0, a \ne 1, f(x) = a^x, f^{-1}(x) = \log_a(x)$.

Graphical Interpretation

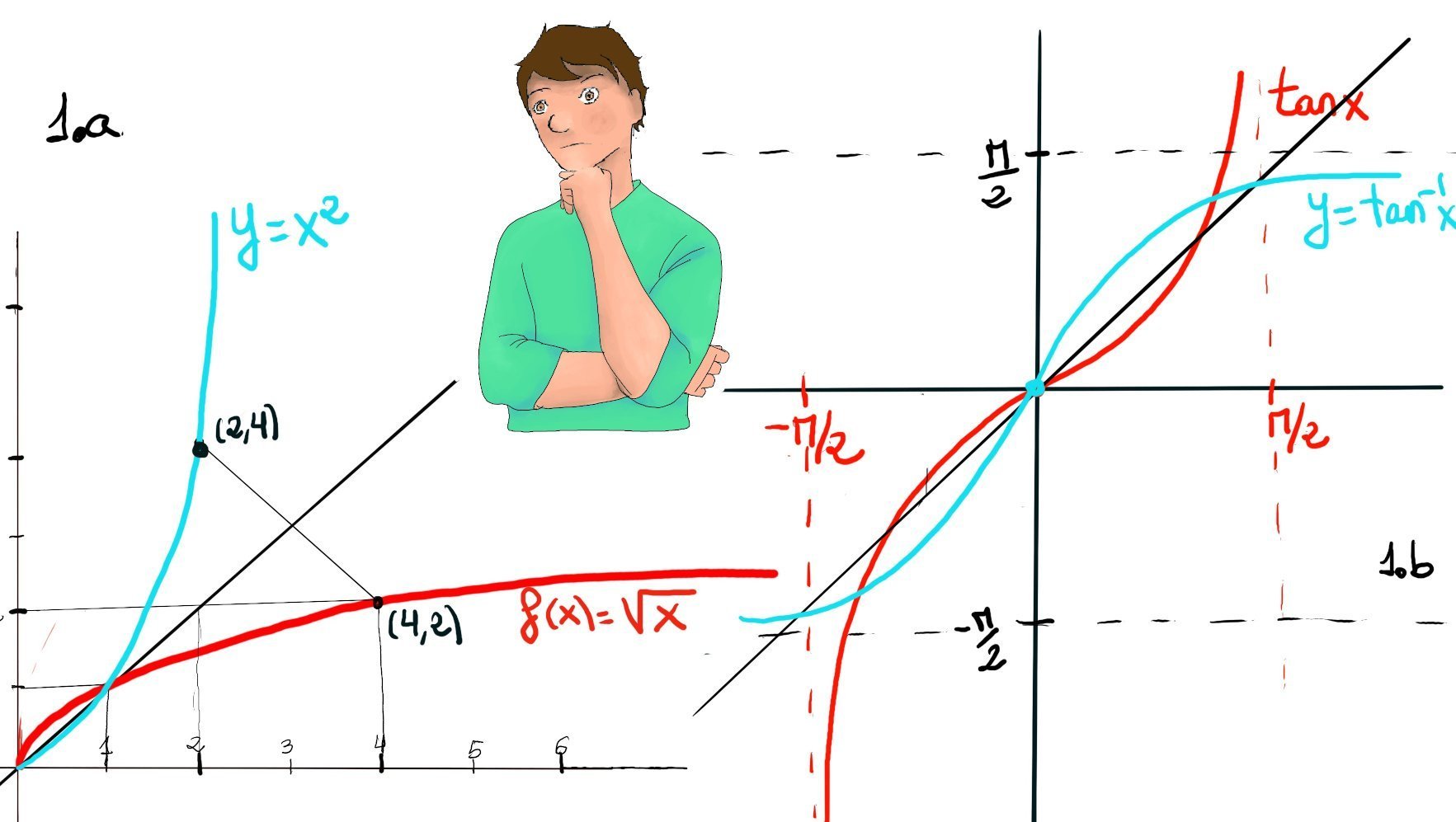
To plot the graph of f^-1, you just need to reflect the graph of f(x) about the line y = x. Every point (x, f(x)) becomes (f(x), x), e.g., $(2, 8)$ on $y = x^3$ and $(8, 2)$ on $y = \sqrt[3]{x}$. The graphs of $f$ and $f^{-1}$ are mirror images across the line $y = x$.

Finding Inverse Functions

To find the inverse of a function, you need to switch the roles of x and y, and then solve for y in terms of x.

Rational Function. f(x) = $\frac{2x+5}{3x-2}$.

1. Write $y = f(x)$. Let $y = \dfrac{2x+5}{3x-2}$
2. Swap $x$ and $y$. $x = \frac{2y+5}{3y-2}$
3. Solve for y. $3yx -2x = 2y + 5 \implies y(3x-2) = 2x + 5 \implies y = \frac{2x + 5}{3x - 2}$.
4. Write $f^{-1}(x) = y$. $f^{-1}(x) = \frac{2x+5}{3x-2}.$

   This function is its own inverse! Such functions are called involutions.

Cubic Function. f(x) = x³ -1.

1. Write $y = f(x)$. Let $y = x^3 - 1$
2. Swap $x$ and $y$. $x = y^3 - 1$
3. Solve for y. $y^3 = x + 1 \implies y = \sqrt[3]{x+1}$
4. Write $f^{-1}(x) = y$. $f^{-1}(x) = \sqrt[3]{x+1}$

Derivate of inverse functions

The Inverse function theorem. Let f(x) be a function that is both invertible and differentiable and let $f^{-1}(x)$ be the inverse of f. Then, for all x satisfying $f'(f^{-1}(x)) \ne 0, f^{(-1)'}(x) = \frac{1}{f'(f^{-1}(x))}$.

Proof.

By definition of inverse y = f^-1(x) ↭ x = f(y).

We differentiate both sides implicitly with respect to x using the Chain Rule: 1 = $f'(y)·\frac{dy}{dx} ⇒[\text{Solve for } \dfrac{dy}{dx}] \frac{dy}{dx} = \frac{1}{f'(y)}$ ⇒[Substitute y = f^-1(x)] $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} \quad \blacksquare$

Geometric interpretation

At corresponding points $(a, b)$ on $f$ and $(b, a)$ on $f^{-1}$:

At corresponding points: If f(a) = b, then $f^{-1}(b) = a$. The slopes at those points satisfy: $f'(a) \cdot (f^{-1})'(b) = 1, (f^{-1})'(b) = \frac{1}{f'(a)}$. So the tangent line to $f^{-1}$ at (b, a) is the reflection of the tangent line to f at (a, b) across y = x, so their slopes are reciprocal.

Solved examples

• $f(x) = x^3$. $f'(x) = 3x^2$. Find the inverse: $f^{-1}(x) = \sqrt[3]{x} = x^{1/3}$. Apply the theorem: $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{3(f^{-1}(x))^2} = \frac{1}{3(x^{1/3})^2} = \frac{1}{3x^{2/3}}$. Verify directly: $\frac{d}{dx}[x^{1/3}] = \frac{1}{3}x^{-2/3} = \frac{1}{3x^{2/3}} \quad \checkmark$.

• Let $f(x) = x^3 - 1$, with inverse $f^{-1}(x) = \sqrt[3]{x+1}$. f’(x) = $3x^2$. Then, for any x, $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{3(f^{-1}(x))^2} = \frac{1}{3(\sqrt[3]{x+1})^2} = \frac{1}{3(x+1)^{2/3}}.$ If we differentiate $f^{-1}(x) = (x+1)^{1/3}$ directly: $\frac{d}{dx}(x+1)^{1/3} = \frac{1}{3}(x+1)^{-2/3} = \frac{1}{3(x+1)^{2/3}} \quad \checkmark$.

• Derivative at a Specific Point. Let f(x) = 3·x³+2x+2. Compute (f^-1)’(2).

f’(x) = 9x² + 2. We need to calculate f^-1(2): y = 3·x³+2x+2, we swap x↭y, x = 3·y³+2y+2, $2 = 3y^3+2y+2 \implies (3y^2+2)y + 0$. Since $3y^2+2 \ge 0$, the only solution is 0.

By the inverse function theorem, the derivative of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{9y^2+2}$ where y = f^-1(x). Thus, $f^{-1'}(2) = \frac{1}{9·0^2+2}= \frac{1}{2}$

• Let $f(x) = e^x$. Then, $f^{-1}(x) = \ln(x)$, for x > 0. $f'(x) = e^x$. Using the inverse derivative formula: $(\ln (x))' = (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{e^{\ln(x)}} = \frac{1}{x}.$

• Let f(x) = x⁵+2x³+7x+1. Compute (f^-1)’(1).

f’(x) = 5x⁴ + 8x² + 7. The derivate of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4+8y^2+7}$ where y = f^-1(x).

(f^-1)’(1) =[It is easy to notice that f(0) = 1, hence f^-1(1) = 0] $\frac{1}{5·0^4+8·0^2+7} = \frac{1}{7}$.

• Find the equation of the tangent line to the inverse of y = f(x) = $x^5-2x^3+3x+2$ at P(4, 1)

It is important to realize that P(4, 1) lies on f^-1, since f(1) = 1 -2 +3 +2 = 4, f^-1(4) = 1.

f(x) = $x^5-2x^3+3x+2 ⇒ f'(x) = 5x^4-6x^2+3$. By the inverse function theorem, the derivate of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4-6y^2+3}$ where y = f^-1(x).

(f^-1)’(4) =[f^-1(4) = 1] $\frac{1}{5·1^4-6·1^2+3} = \frac{1}{2}$.

The equation of the tangent line to the graph of f^-1 at P(4, 1) is (using point-slope form) y -y₀ = m(x -x₀), that is y -1 = ¹⁄₂(x -4), which simplifies to y = ¹⁄₂x -1.

• Use the inverse function theorem to find the derivate of $\sqrt[3]{x}.$

The function $\sqrt[3]{x}$ is the inverse of the function f(x) = x³, and we know that f’(x) = 3x².

By the inverse function theorem, $\frac{d}{dx} f^{-1}(x) = \frac{1}{3y^2}$ =[y = f^-1(x)] $\frac{1}{3·(\sqrt[3]{x})^2} = \frac{1}{3·x^{\frac{2}{3}}} = \frac{1}{3}x^{\frac{-2}{3}}$

Derivatives of Inverse Trigonometric Functions

Inverse trigonometric functions (arcsine, arccosine, arctangent, etc.) are the inverses of the basic trigonometric functions, defined on appropriate principal branches so they are single-valued. If y = arcsin(x) (also written $y =\sin^{-1}(x)$), then $\sin(y) = x$. We often differentiate such equalities implicitly and then solve for dy/dx.

• y = tan^-1x ⇨ tan(y) = x (where $\frac{\pi}{2} \lt y \lt \frac{\pi}{2}$).

$\frac{d}{dx}(tan(y)=x) \implies[\text{Differentiate implicitly: }] \frac{1}{cos^{2}y}\frac{dy}{dx}=1 \implies \frac{dy}{dx}=cos^{2}y=\frac{1}{sec^2(y)}$

$(tan^{-1}x)'=\frac{d}{dx}\tan^{-1}x=cos^{2}(y)$ [tan(y) = x ↭ $ \frac{sin(y)}{cos(y)} = x ⇒ sin(y) = x·cos(y) ⇒ (x·cos(y))^2+cos^2(y) = 1 ⇒ x^2·cos^2(y) +cos^2(y) = 1 ⇒ (x^2+1)·cos^2(y) = 1 ⇒ cos(y) = \frac{1}{\sqrt{1+x^{2}}}$] = $\frac{1}{1+x^{2}}$

$\boxed{\frac{d}{dx}(arctan(x)) = \frac{1}{1+x^2}}$

• y = $tan^{-1}(\frac{1}{x+1})$. Let u = $\frac{1}{x+1} = (x+1)^{-1}⇒ u' = (-1)·(x+1)^{-2}$

By the previous result and the chain rule, y’ = $\frac{1}{1+(\frac{1}{x+1})^{2}}·\frac{-1}{(x+1)^{2}} = \frac{1}{\frac{(x+1)^2+1}{(x+1)^2}}·\frac{-1}{(x+1)^{2}} = \frac{-1}{(x+1)^2+1} = \frac{-1}{x^2+2x+2}$

• y = sin^-1x ⇨ siny = x.

$\frac{d}{dx}siny=1⇨~ \frac{d}{dy}siny\frac{dy}{dx}=1⇨~ cosy\frac{dy}{dx}=1$

$y'= \frac{1}{cos(y)}=~ \frac{1}{\sqrt{1-sin^{2}y}}=~ \frac{1}{\sqrt{1-x^{2}}}$

$(sin^{-1}x)'=\frac{d}{dx}sin^{-1}x=~ \frac{1}{\sqrt{1-x^{2}}}$

• y = sin^-1(x³) ⇨ sin(y) = x³.

$\frac{d}{dx}sin(y) = 3x^2 ⇨~ \frac{d}{dy}sin(y)\frac{dy}{dx}=3x^2 ⇨~ cos(y)\frac{dy}{dx}=3x^2$

$(sin^{-1}(x^3))'=\frac{d}{dx}sin^{-1}(x^3)=~ \frac{3x^2}{cos(y)} = \frac{3x^2}{\sqrt{1-sin^{2}y}} = \frac{3x^2}{\sqrt{1-(x^3)^2}} = \frac{3x^2}{\sqrt{1-x^6}}$

• y = cos^-1(x) ⇒ cos(y) = x.

$\frac{d}{dx}cos(y) = 1 ⇨~ \frac{d}{dy}cos(y)\frac{dy}{dx}=1 ⇨~ -sin(y)\frac{dy}{dx}=1$

$(cos^{-1}(x))'=\frac{d}{dx}cos^{-1}(x)=~ \frac{-1}{sin(y)} = \frac{-1}{\sqrt{1-cos^{2}y}} = \frac{-1}{\sqrt{1-x^2}}.$

• y = cos^-1(5x -9) ⇒ cos(y) = 5x -9.

$\frac{d}{dx}cos(y) = 5 ⇨~ \frac{d}{dy}cos(y)\frac{dy}{dx}=5 ⇨~ -sin(y)\frac{dy}{dx}=5$

$(cos^{-1}(5x-9))'=\frac{d}{dx}cos^{-1}(5x-9)=~ \frac{-5}{sin(y)} = \frac{-5}{\sqrt{1-cos^{2}y}} = \frac{-5}{\sqrt{1-(5x-9)^2}}.$

• The secant is the reciprocal of the cosine, i.e., the ratio of the hypotenuse to the side adjacent to a given angle in a right triangle. y = secx = $\frac{1}{cosx} = (cosx)^{-1}$.

$\frac{d}{dx}secx =~(-1)(cosx)^{-2}(-sin(x))=\frac{sin(x)}{cos(x)^{2}}=\frac{1}{cos(x)}·\frac{sin(x)}{cos(x)} = sec(x)·tan(x).$

• $\frac{d}{dx}ln(secx)=\frac{(secx)'}{secx}=\frac{secx·tanx}{secx}=tanx$

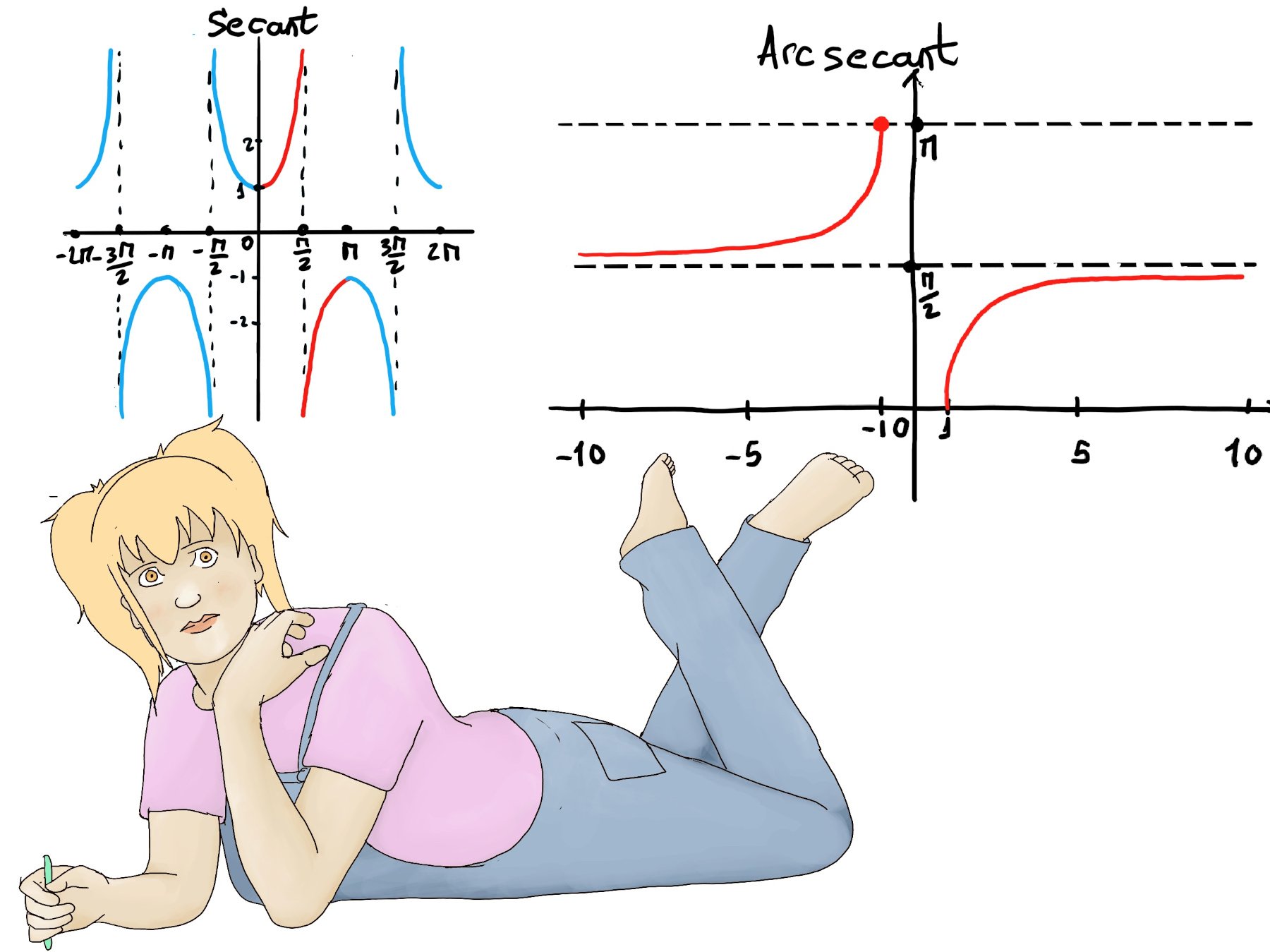
• The cosecant is the reciprocal of the sine, i.e., the ratio of the hypotenuse to the side opposite a given angle in a right triangle. The arcsecant is the inverse of the secant function, y = csc^-1(x) = arcsin(¹⁄_x) ⇒[$(sin^{-1}x)'= \frac{1}{\sqrt{1-x^{2}}}$ and the Chain Rule] y’ = $\frac{1}{\sqrt{1-(\frac{1}{x})^{2}}}·\frac{-1}{x^2} = \frac{1}{\sqrt{\frac{x^2-1}{x^2}}}·\frac{-1}{x^2} = \frac{-1}{\frac{x^2\sqrt{x^2-1}}{|x|}} = \frac{-1}{\frac{|x||x|\sqrt{x^2-1}}{|x|}} = \frac{-1}{|x|\sqrt{x^2-1}}$

This expression holds true when x > 1 or x < -1 as the expression involves the square root of x² - 1, which must be non-negative.

$y' = \begin{cases} \frac{1}{x\sqrt{x^2-1}}, &x > 1 \\\\ \frac{-1}{x\sqrt{x^2-1}}, &x < -1 \end{cases}$

x > 1 ↭ 0 < arcsec(x) < ^π⁄₂, x < -1 ↭ ^π⁄₂ < arcsec(x) < π, Derivative of Arcsecant Function, ProofWiki

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.