|
 |

|
The man who asks a question is a fool for a minute, the man who does not ask is a fool for life, Confucius.

The derivative of a function at a specific input value describes the instantaneous rate of change. Geometrically, when the derivative exists, it is the slope of the tangent line to the graph of the function at that point. Algebraically, it represents the ratio of the change in the dependent variable to the change in the independent variable as the change approaches zero.
Definition. A function f(x) is differentiable at a point “a” in its domain, if its domain contains an open interval around “a”, and the following limit exists $f'(a) = L = \lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then the following inequality holds |L-$\frac {f(a+h)-f(a)}{h}$|< ε.
The inverse function of a function f is a function that undoes the operation of the original function. If f maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted as $f^{-1}$, maps each element y back to its corresponding x: $y = f(x) \iff x = f^{-1}(y)$
The Fundamental Property. For a given function f, its inverse f-1 is a function that reverses its result (f-1 reverses the input and output of the original function): $f^{-1}(f(x)) = x \quad \text{and} \quad f(f^{-1}(x)) = x$
For an inverse function to exist, the original function must be both one-to-one (injective) and onto (surjective).
| Function $f(x)$ | Inverse $f^{-1}(x)$ | Domain Restriction |
|---|---|---|
| $x^2$ | $\sqrt{x}$ | $x \geq 0$ |
| $x^3$ | $\sqrt[3]{x}$ | All $\mathbb{R}$ |
| $e^x$ | $\ln(x)$ | $x > 0$ for $\ln$ |
| $a^x$ | $\log_a(x)$ | $x > 0$ for $\log$ |
| $\sin(x)$ | $\arcsin(x)$ | $[-\frac{\pi}{2}, \frac{\pi}{2}]$ for $\sin$ |
| $\cos(x)$ | $\arccos(x)$ | $[0, \pi]$ for $\cos$ |
| $\tan(x)$ | $\arctan(x)$ | $(-\frac{\pi}{2}, \frac{\pi}{2})$ for $\tan$ |
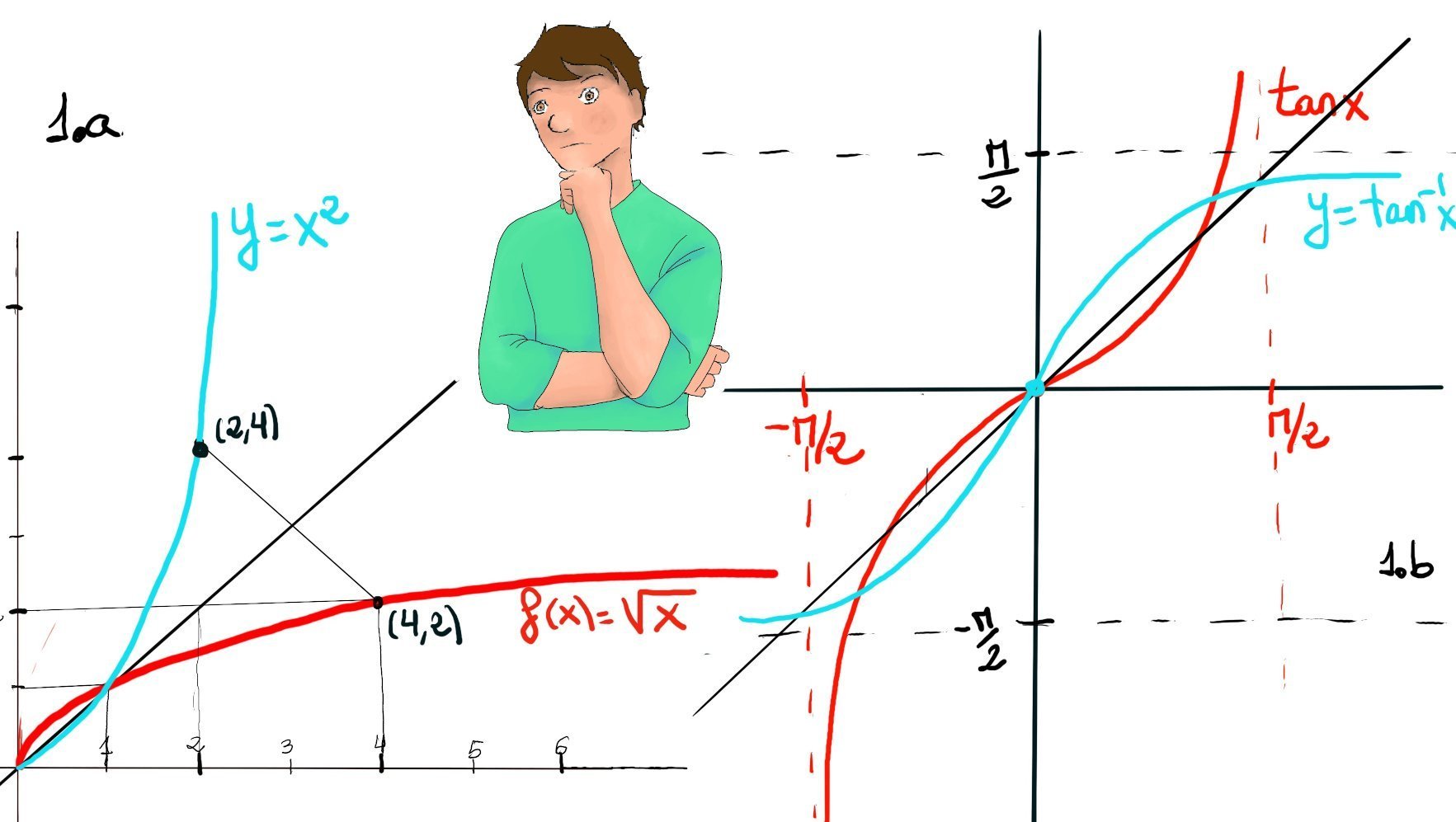
To plot the graph of f-1, you just need to reflect the graph of f(x) about the line y = x. Every point (x, f(x)) becomes (f(x), x), e.g., $(2, 8)$ on $y = x^3$ and $(8, 2)$ on $y = \sqrt[3]{x}$. The graphs of $f$ and $f^{-1}$ are mirror images across the line $y = x$.
To find the inverse of a function, you need to switch the roles of x and y, and then solve for y in terms of x.
Rational Function. f(x) = $\frac{2x+5}{3x-2}$.
This function is its own inverse! Such functions are called involutions.
Cubic Function. f(x) = x3 -1.
The Inverse function theorem. Let f(x) be a function that is both invertible and differentiable and let $f^{-1}(x)$ be the inverse of f. Then, for all x satisfying $f'(f^{-1}(x)) \ne 0, f^{(-1)'}(x) = \frac{1}{f'(f^{-1}(x))}$.
Proof.
By definition of inverse y = f-1(x) ↭ x = f(y).
We differentiate both sides implicitly with respect to x using the Chain Rule: 1 = $f'(y)·\frac{dy}{dx} ⇒[\text{Solve for } \dfrac{dy}{dx}] \frac{dy}{dx} = \frac{1}{f'(y)}$ ⇒[Substitute y = f-1(x)] $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} \quad \blacksquare$
At corresponding points $(a, b)$ on $f$ and $(b, a)$ on $f^{-1}$:
| Function | Point | Slope |
|---|---|---|
| $f$ | $(a, b)$ | $f'(a) = m$ |
| $f^{-1}$ | $(b, a)$ | $(f^{-1})'(b) = \dfrac{1}{m}$ |
At corresponding points: If f(a) = b, then $f^{-1}(b) = a$. The slopes at those points satisfy: $f'(a) \cdot (f^{-1})'(b) = 1, (f^{-1})'(b) = \frac{1}{f'(a)}$. So the tangent line to $f^{-1}$ at (b, a) is the reflection of the tangent line to f at (a, b) across y = x, so their slopes are reciprocal.
$f(x) = x^3$. $f'(x) = 3x^2$. Find the inverse: $f^{-1}(x) = \sqrt[3]{x} = x^{1/3}$. Apply the theorem: $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{3(f^{-1}(x))^2} = \frac{1}{3(x^{1/3})^2} = \frac{1}{3x^{2/3}}$. Verify directly: $\frac{d}{dx}[x^{1/3}] = \frac{1}{3}x^{-2/3} = \frac{1}{3x^{2/3}} \quad \checkmark$.
Let $f(x) = x^3 - 1$, with inverse $f^{-1}(x) = \sqrt[3]{x+1}$. f’(x) = $3x^2$. Then, for any x, $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{3(f^{-1}(x))^2} = \frac{1}{3(\sqrt[3]{x+1})^2} = \frac{1}{3(x+1)^{2/3}}.$ If we differentiate $f^{-1}(x) = (x+1)^{1/3}$ directly: $\frac{d}{dx}(x+1)^{1/3} = \frac{1}{3}(x+1)^{-2/3} = \frac{1}{3(x+1)^{2/3}} \quad \checkmark$.
Derivative at a Specific Point. Let f(x) = 3·x3+2x+2. Compute (f-1)’(2).
f’(x) = 9x2 + 2. We need to calculate f-1(2): y = 3·x3+2x+2, we swap x↭y, x = 3·y3+2y+2, $2 = 3y^3+2y+2 \implies (3y^2+2)y + 0$. Since $3y^2+2 \ge 0$, the only solution is 0.
By the inverse function theorem, the derivative of f-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{9y^2+2}$ where y = f-1(x). Thus, $f^{-1'}(2) = \frac{1}{9·0^2+2}= \frac{1}{2}$
Let $f(x) = e^x$. Then, $f^{-1}(x) = \ln(x)$, for x > 0. $f'(x) = e^x$. Using the inverse derivative formula: $(\ln (x))' = (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{e^{\ln(x)}} = \frac{1}{x}.$
Let f(x) = x5+2x3+7x+1. Compute (f-1)’(1).
f’(x) = 5x4 + 8x2 + 7. The derivate of f-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4+8y^2+7}$ where y = f-1(x).
(f-1)’(1) =[It is easy to notice that f(0) = 1, hence f-1(1) = 0] $\frac{1}{5·0^4+8·0^2+7} = \frac{1}{7}$.
It is important to realize that P(4, 1) lies on f-1, since f(1) = 1 -2 +3 +2 = 4, f-1(4) = 1.
f(x) = $x^5-2x^3+3x+2 ⇒ f'(x) = 5x^4-6x^2+3$. By the inverse function theorem, the derivate of f-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4-6y^2+3}$ where y = f-1(x).
(f-1)’(4) =[f-1(4) = 1] $\frac{1}{5·1^4-6·1^2+3} = \frac{1}{2}$.
The equation of the tangent line to the graph of f-1 at P(4, 1) is (using point-slope form) y -y0 = m(x -x0), that is y -1 = 1⁄2(x -4), which simplifies to y = 1⁄2x -1.
The function $\sqrt[3]{x}$ is the inverse of the function f(x) = x3, and we know that f’(x) = 3x2.
By the inverse function theorem, $\frac{d}{dx} f^{-1}(x) = \frac{1}{3y^2}$ =[y = f-1(x)] $\frac{1}{3·(\sqrt[3]{x})^2} = \frac{1}{3·x^{\frac{2}{3}}} = \frac{1}{3}x^{\frac{-2}{3}}$
Inverse trigonometric functions (arcsine, arccosine, arctangent, etc.) are the inverses of the basic trigonometric functions, defined on appropriate principal branches so they are single-valued. If y = arcsin(x) (also written $y =\sin^{-1}(x)$), then $\sin(y) = x$. We often differentiate such equalities implicitly and then solve for dy/dx.
y = tan-1x ⇨ tan(y) = x (where $\frac{\pi}{2} \lt y \lt \frac{\pi}{2}$).
$\frac{d}{dx}(tan(y)=x) \implies[\text{Differentiate implicitly: }] \frac{1}{cos^{2}y}\frac{dy}{dx}=1 \implies \frac{dy}{dx}=cos^{2}y=\frac{1}{sec^2(y)}$
$(tan^{-1}x)'=\frac{d}{dx}\tan^{-1}x=cos^{2}(y)$ [tan(y) = x ↭ $ \frac{sin(y)}{cos(y)} = x ⇒ sin(y) = x·cos(y) ⇒ (x·cos(y))^2+cos^2(y) = 1 ⇒ x^2·cos^2(y) +cos^2(y) = 1 ⇒ (x^2+1)·cos^2(y) = 1 ⇒ cos(y) = \frac{1}{\sqrt{1+x^{2}}}$] = $\frac{1}{1+x^{2}}$
$\boxed{\frac{d}{dx}(arctan(x)) = \frac{1}{1+x^2}}, \forall x \in \mathbb{R}$.
The derivate of $tan^{-1}(u)$ is $\frac{1}{1+u^2}$, so using the chain rule we get:
$$ \begin{aligned} y' &=\frac{1}{1+(\frac{1}{x+1})^{2}}·\frac{-1}{(x+1)^{2}} \\[2pt] &\text{Simplify the fraction: } 1+ \frac{1}{(x+1)^2} = \frac{(x+1)^2 + 1}{(x+1)^2}\\[2pt] &=\frac{1}{\frac{(x+1)^2+1}{(x+1)^2}}·\frac{-1}{(x+1)^{2}} = \frac{(x+1)^2}{(x+1)^2+1}·\frac{-1}{(x+1)^{2}} \\[2pt] &= \frac{-1}{(x+1)^2+1} = \frac{-1}{x^2+2x+2}. \end{aligned} $$The derivative exists for all $x \ne -1$ (since the original function is undefined at x = −1), and the denominator $x^2 + 2x + 2$ is always positive because its discriminant is negative.
Let y = sin-1(x), so sin(y) = x.
Differentiate: $\cos(y)\frac{dy}{dx}=1 \implies \frac{dy}{dx} = \frac{1}{\cos(y)}$
$y \in [-\frac{\pi}{2}, \frac{\pi}{2}] \implies \cos(y) \ge 0 \text{ and } \cos(y) = \sqrt{1-sin^2(y)}=\sqrt{1-x^2}$. Hence, $\boxed{\frac{d}{dx}arcsin(x) = \frac{1}{\sqrt{1-x^2}}, |x| \lt 1}$
$y'= \frac{1}{cos(y)}=~ \frac{1}{\sqrt{1-sin^{2}y}}=~ \frac{1}{\sqrt{1-x^{2}}}$
f(x) = sin(x) on [-π/2, π/2], so $f^{-1}(x) = arcsin(x)$. (i) f’(x) = cos(x); (ii) Let y = arcsin(x), so sin(y) = x; (iii) Apply the inverse function theorem, $(sin^{-1}x)'=\frac{d}{dx}sin^{-1}x=\frac{1}{cos(sin^{-1}(x))} = \frac{1}{cos(y)} =[\cos(y) =\frac{1}{\sqrt{1-x^2}}] \frac{1}{\sqrt{1-x^{2}}} \checkmark$
Differentiating implicitly with respect to x: $\frac{d}{dx}sin(y) = 3x^2 \implies cos(y)\frac{dy}{dx}=3x^2 \implies \frac{dy}{dx} = \frac{3x^2}{cos(y)}$
Since cos(y) ≥ 0 on the range of arcsin, we have $\cos(y) = \sqrt{1-sin^2(y)} = \sqrt{1-(x^3)^2}=\sqrt{1-x^6}$
Substituting, $(sin^{-1}(x^3))' = \frac{3x^2}{cos(y)} = \frac{3x^2}{\sqrt{1-x^6}}$. This holds for $|x^3| \lt 1$ (where arcsin is defined), i.e., |x| < 1.
y = cos-1(x) ⇒ cos(y) = x for y∈[0, π], x∈[−1, 1].
Differentiate both sides with respect to x (by chain rule): $\frac{d}{dx}\cos(y) = 1 \implies -\sin(y)\frac{dy}{dx} = 1 \implies \frac{dy}{dx} = -\frac{1}{\sin(y)}$
Since $y \in [0, \pi] \implies \sin(y) \ge 0 \text{ and } \sin(y) =[\text{Use the Pythagorean identity:}] \sqrt{1-\cos^2(y)}=\sqrt{1-x^2}$. Thus,
$(cos^{-1}(x))'=\frac{d}{dx}cos^{-1}(x)=~ \frac{-1}{sin(y)} = \frac{-1}{\sqrt{1-x^2}}, \boxed{\frac{d}{dx}arccos(x)=-\frac{1}{\sqrt{1-x^2}}}, |x| \lt 1$.
f(x) = cos(x) on [0, π], so $f^{-1}(x) = arccos(x)$. (i) f’(x) = -sin(x) (non-zero on (0, π), so inverse exists).; (ii) Let y = arccos(x), so cos(y) = x; (iii) Apply the inverse function theorem, $(cos^{-1}x)'=\frac{d}{dx}cos^{-1}x=\frac{1}{-sin(cos^{-1}(x))} = \frac{-1}{sin(y)} =[\sin(y) =\frac{1}{\sqrt{1-x^2}}] \frac{-1}{\sqrt{1-x^{2}}} \checkmark$
Implicit Differentiation: $\frac{d}{dx}\cos(y) = 5 \implies[\text{Chain Rule}] -\sin(y)\frac{dy}{dx} = 5 \implies[\text{Solve for } \frac{dy}{dx}] \frac{dy}{dx} = -\frac{5}{\sin(y)}$.
Since $y \in [0, \pi] \implies \sin(y) \ge 0 \text{ and } \sin(y) =[\text{Use the Pythagorean identity:}] \sqrt{1-\cos^2(y)}=\sqrt{1-(5x-9)^2}$. Thus,
Substitute sin(y) into the derivative: $(cos^{-1}(5x-9))'=\frac{d}{dx}cos^{-1}(5x-9)=\frac{-5}{sin(y)} = \frac{-5}{\sqrt{1-(5x-9)^2}},$ valid for $|5x-9| \lt 1$
The expression under the square root must be positive: $1-(5x-9)^2 \gt 0 \implies |5x-9| \lt 1 \implies −1 < 5x−9 < 1 \implies 8 \lt 5x \lt 10 \implies \frac{8}{5} \lt x \lt 2$.
$\frac{d}{dx}sec(x) =[\text{Power rule, Chain rule}] (-1)(cos(x))^{-2}(-sin(x))=\frac{sin(x)}{cos(x)^{2}}=\frac{1}{cos(x)}·\frac{sin(x)}{cos(x)} = sec(x)·tan(x) \text{ for } x \ne \frac{\pi}{2}+k\pi, k \in \mathbb{Z}.$
$\frac{d}{dx}ln(sec(x)) =[\text{Apply the chain rule}] \frac{(sec(x))'}{sec(x)} =[\text{Substitute the derivative of sec(x):}] \frac{sec(x)·tan(x)}{sec(x)} =[\text{Simplify}] tan(x)$
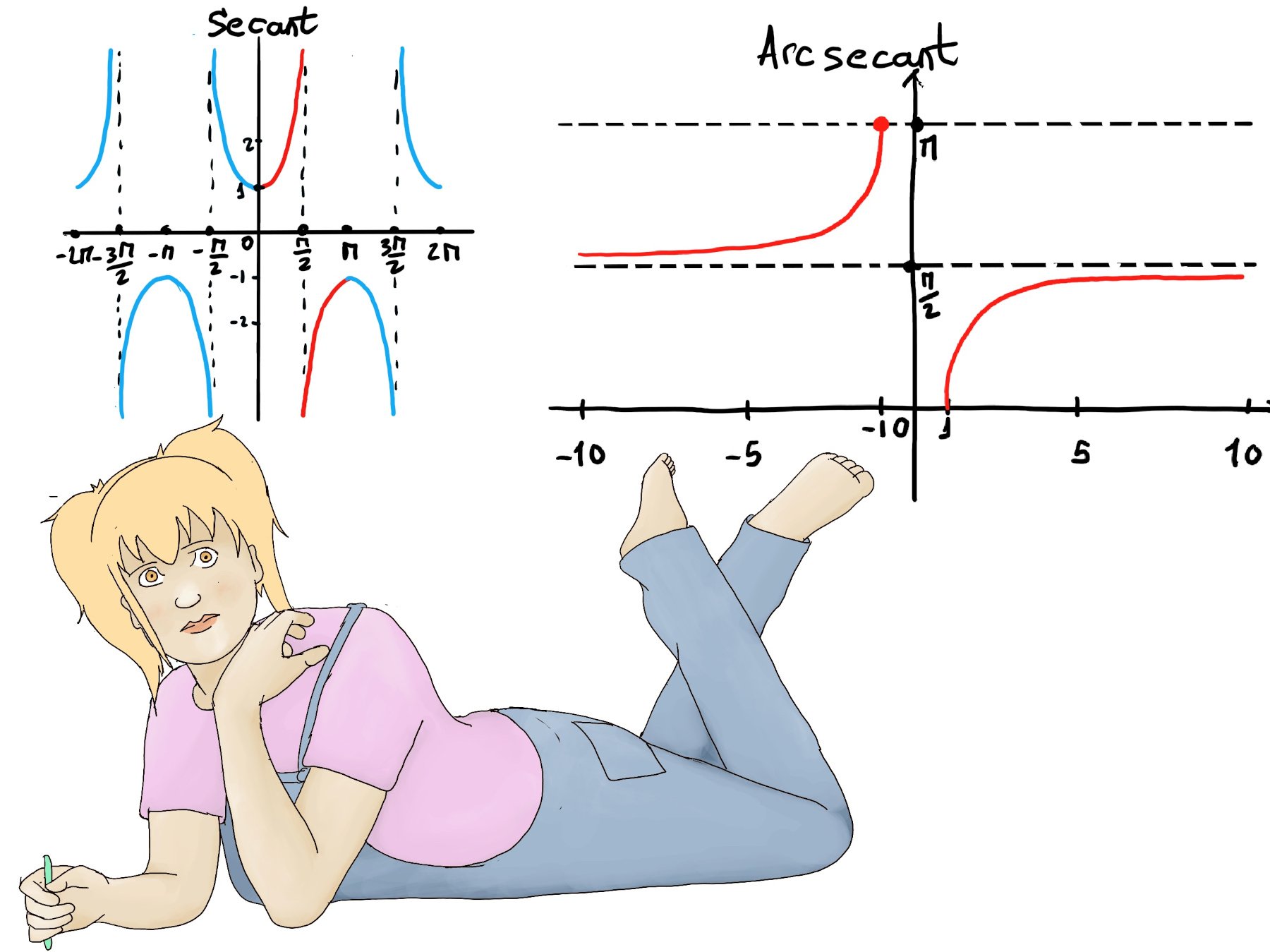
The cosecant function, denoted csc(x), is the reciprocal of the sine function, i.e., the ratio of the hypotenuse to the opposite side to a given angle in a right triangle. $csc(x) = \frac{1}{sin(x)} = \frac{\text{hypotenuse}}{\text{opposite side}}$. Domain: $x \ne k\pi, k \in \mathbb{Z}$. Range: (−∞, −1] ∪ [1, ∞).
Derivative of csc(x): Using the chain rule: $\frac{d}{dx}csc(x) = -1 \cdot (sin(x))^{-2}\cdot cos(x) = -\frac{cos(x)}{sin^2(x)} = -csc(x)cot(x)$
y = arcsec(x) = arccos(1/x) ⇒ y’ = $-\frac{1}{\sqrt{1-(\frac{1}{x})^{2}}}·\frac{-1}{x^2} = \frac{1}{x^2\sqrt{\frac{x^2-1}{x^2}}}$ =
Since $\sqrt{x^2}=|x|$ (the square root function returns the non-negative square root, and |x| is the non-negative value whose square is $x^2$) and $\frac{|x|}{x^2} = \frac{|x|}{|x|^2} = \frac{1}{|x|}$
$\frac{1}{x^2\frac{\sqrt{x^2-1}}{|x|}} = \frac{|x|}{x^2\sqrt{x^2-1}} = \frac{1}{|x|\sqrt{x^2-1}}$