Continuity and discontinuity

You’ve gotta dance like there’s nobody watching, love like you’ll never be hurt,sing like there’s nobody listening, and live like it’s heaven on earth, William W. Purkey.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element x in a set D, x ∈ D (called the domain) exactly one element y in a set E, y ∈ E (called the codomain or range).

• The pair (x, y) is denoted as y = f(x) where: x is the independent variable (input) and y is the dependent variable (output). Often, both the domain D and codomain E are the set of real numbers ℝ or subsets of ℝ. A mathematical function can be thought of as a black box (or machine) that takes an input from its domain and produces exactly one output in its codomain. Inside the machine lives a specific rule (formula, procedure, or mapping) that dictates or tells you which output corresponds to each input, and a key property is uniqueness —each input maps to a single, deterministic output. No input can ever produce two different results (Figure E). The function f(x) = x² accepts any real number x (domain: ℝ) and returns exactly one non-negative value x² (output in codomain: [0,∞)). The input 3 always yields 9, never any other value.

• D is the domain, the set of all possible inputs. E is the codomain or range, the set of all possible outputs.

• Key property💡: Each input has exactly one output. (No input is assigned two different outputs — this is the vertical line test!)

• Examples: constant, f(x) = c, horizontal line, slope = 0; linear, f(x) = mx + b, straight line, constant slope m and y-intercept b; quadratic $f(x) = ax^2 + bx + c$, u-shaped or inverted U, opens up (a > 0) or down (a < 0), vertex at x = $\frac{-b}{2a}$, symmetry about vertical axis through vertex; polynomial, $f(x) = a_n x^n + \dots + a_0$, a smooth and continuous curve, n roots (counting multiplicity), end behaviour determined by its leading term $a_n x^n$; exponential function, $f(x) = a \cdot b^x, a \ne 0, b \gt 0$, rapid growth (b > 1) or decay (0 < b < 1); trigonometric functions, $\sin(x), \cos(x), \tan (z)$ oscillatory, periodic behavior (period 2π for sin/cos, π for tan), sin and cos are bounded between -1 and 1, but tan is unbounded; step function $f(x) = \lfloor x \rfloor$, greatest integer ≤ x, constant on intervals [n, n+1), jumps at integers, its graph is a staircase shape; absolute value f(x) = |x|, V-shaped graph, slope changes at 0.

• Functions can be expressed in multiple forms, each useful in different contexts: verbal description, table of values (list of pairs), algebraic formula, graph, piecewise definition, recursive definition, parametric or integral form, and series representation.

• Evaluating a function means finding or computing the output value f(x) for a given input value x. f(x) = $x^2-2x +4, f(2) = 2^2 -2\cdot 2 + 4 = 4 - 4 + 4 = 4, f(0) = 0^2 -2\cdot 0 + 4 = 4, f(1) = 1^2 -2\cdot 1 + 4 = 1 -2 +4 = 3$

• The x-intercept is any point on the graph that intersects or crosses the x-axis. In other words, it is the value of x when the function (y-coordinate or y-value) is zero. The y-intercept is the point where the graph intersects or crosses the y-axis. y-coordinate of the point whose x-coordinate is 0, e.g., 2x - 3y = 6. x-intercept: set y = 0 → 2x = 6 ⇒ x=3, so (3, 0). y-intercept: set x = 0 → −3y = 6 ⇒ y = −2, so (0, −2).

• f is said to have a local or relative maximum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≥ f(x) $∀ x \in (a, b) ∩ D$. f is said to have a local or relative minimum at c if there exists an interval (a, b) containing c ($c \in (a, b)$) such that f(c) ≤ f(x) $∀ x \in (a, b) ∩ D$.💡Local extrema can only occur where the function stops rising or falling —either because the derivative is zero, the derivative doesn't exist, or you're at the edge of the domain.

• First Derivative Test. Let f be differentiable on an open interval containing c, except possibly at c itself, and let c be a critical point (so f′(c) = 0 or f′ is undefined). Then:

1. If f′(x) > 0 for x just to the left of c and f′(x) < 0 for x just to the right of c, then f(c) is a local maximum.
2. If f′(x) < 0 for x just to the left of c and f′(x) > 0 for x just to the right of c, then f(c) is a local minimum.
3. If f′(x) does not change sign at c (stays positive or stays negative), then f(c) is not a local extremum.

• Second Derivative Test. If the first derivate of a function at a point c is zero (f'(c) = 0) and the second derivate at this point exists, then: (i) If f''(c) > 0, then f(c) is a local minimum. (ii) If f''(c) < 0, then f(c) is a local maximum. (iii) If f''(c) = 0, the test is inconclusive.
• Vertical asymptotes are vertical lines (perpendicular to the x-axis) of the form x = a (where a is a constant) near which the function grows without bound when x approaches a from at least one side. The line x = a is a vertical asymptote of f if at least one of the one-sided limits is infinite: $\lim_{x \to a^{-}}f(x)=\pm\infty$ or $\lim_{x \to a^{+}}f(x)=\pm\infty$.
• Horizontal asymptotes are horizontal lines (y = c, parallel to the x-axis) that the graph of the function approaches as x grows very large (positively or negatively). In other words, the function values get arbitrarily close to c as long as x is sufficiently large or more formally: $\lim_{x \to \infty}f(x)=c$ and/or $\lim_{x \to -\infty}f(x)=c$.
• A line y = m+b is an oblique (slant) asymptote as $x \to \infty$ if $\lim_{x\to\infty} [f(x) - (mx+b)] = 0.$ This means that the curve of f(x) gets more and more closer to the line y = mx + b as x grows large. For an asymptote y = mx + b as $x \to \infty, m = \lim_{x\to\infty} \frac{f(x)}{x}, b = \lim_{x\to\infty} \bigl(f(x) - m x\bigr)$, provided both limits exist.

Continuity of functions

Continuity is one of the most fundamental ideas in calculus. Intuitively, continuity formalizes the notion of a function whose graph has no breaks, jumps, or gaps, and whose values change smoothly as the input changes.

Definition. A function f(x) is continuous at a point x = a if and only if the following three conditions are satisfied:

• i. The function is defined at that point, i.e., f(a) exists.
• ii. The limit of the function exists at a, $\lim_{x \to a} f(x)$ exists, meaning that both one-sided limits exist and are equal: $\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x)$.
• iii. The value of the function at that point must equal the value of the limit at that point, $\lim_{x \to a} f(x) = f(a).$

A function is continuous at a point if the value of the function agrees with the value the function is approaching. If any one of these conditions fails, the function is discontinuous at x = a.

Continuity on intervals

Definition. A function is continuous on an open interval (a,b) if it is continuous at every point on that interval (a, b).

Definition. A function is continuous on a closed interval [a, b] if it is continuous on the open interval (a,b), continuous from the right at a (i.e., $\lim_{x \to a^+} f(x) = f(a)$), and continuous from the left at b (i.e. $\lim_{x \to b^-} f(x) = f(b)$).

Geometric and intuitive interpretation

Geometrically, you can think of a function that is continuous as a function whose graph has no breaks, holes, or jumps. Intuitively, f is continuous at a if as x gets closer and closer to a, f(x) gets closer and closer to f(a).

Why Continuity Matters

Continuous functions possess key properties that make them indispensable in calculus and applications:

• Intermediate Value Theorem: If f is continuous on [a, b], then for any value L between f(a) and f(b), there exists at least one c ∈ (a,b) such that f(c) = L.
• Extreme Value Theorem: If f is continuous on a closed interval [a, b], then f attains both an absolute maximum and an absolute minimum on that interval.

Formal (ε–δ) definition of continuity

The rigorous definition of continuity is given using ε–δ language.

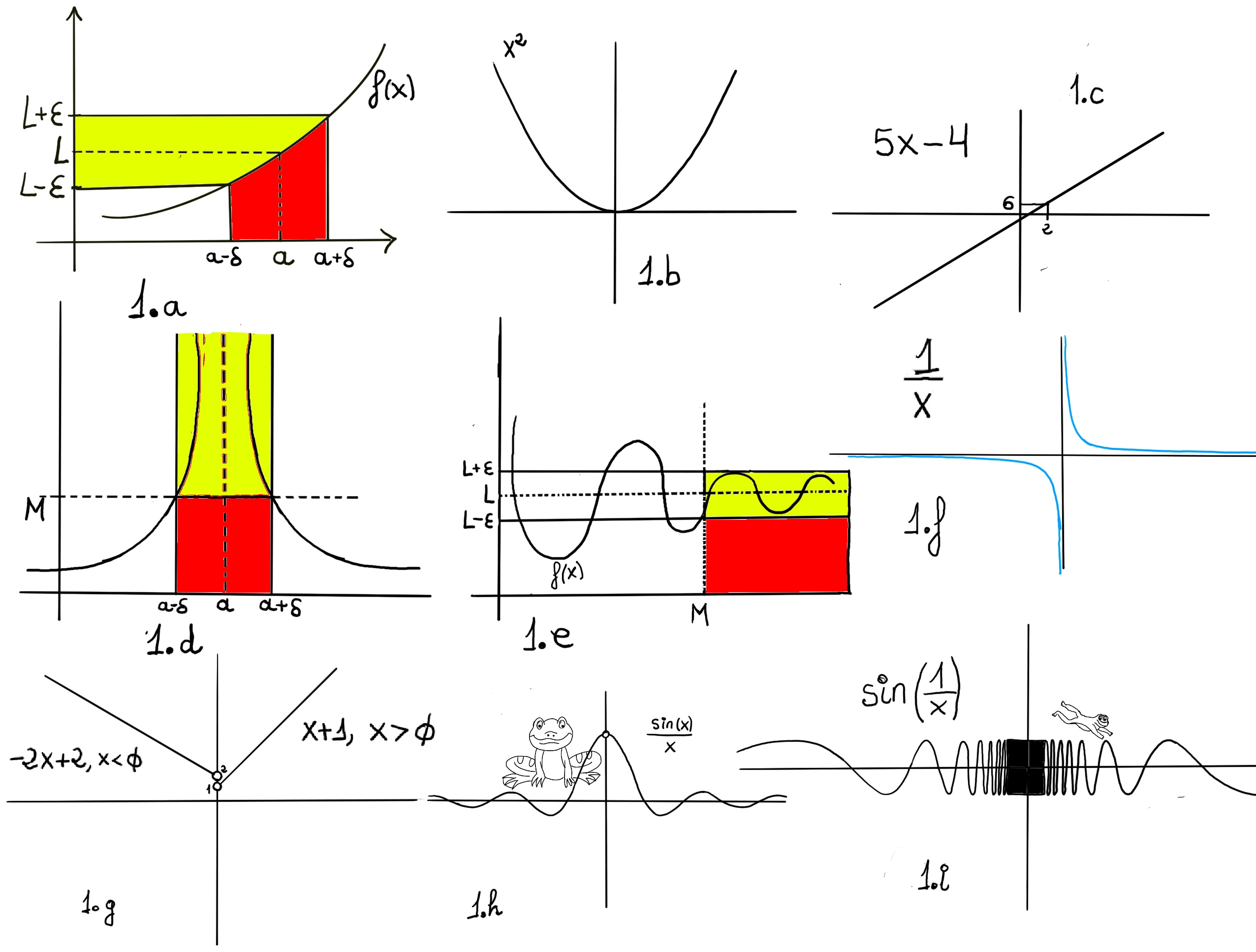
Formally, let f(x) be a function defined on an interval that contains x = a, then we say that f(x) is continuos at x = a, if $\forall \epsilon>0, \exists \delta>0: ~(such~that)~ |f(x)-f(a)|<\epsilon, whenever~ |x-a| < \delta.$ This definition states that we can make f(x) arbitrarily close to f(a) by choosing x sufficiently close to a.

What is a Discontinuous Function?

A function is discontinuous if you cannot draw its graph without lifting your pen. The function’s graph does not form a continuos line, but instead has gaps such as jumps, holes, or breaks. More formally, a function is discontinuous at a point a if it fails to be continuous at a, that is, when it breaks any of the continuity criteria, such as,

• f(a) is not defined, or
• $\lim_{x \to a} f(x)$ does not exist, or
• $\lim_{x \to a} f(x) ≠ f(a).$

Discontinuities appear as holes, jumps, vertical asymptotes, or erratic oscillations.

Types of Discontinuity

Discontinuities can be classified according to how continuity fails.

• A jump discontinuity is a discontinuity where the value of a function “jumps” from one value to another. A function has a jump discontinuity at x = a if both one-sided limits exits, but they are not equal $\lim_{x \to a^-}f(x) \ne \lim_{x \to a^+}f(x)$ Examples:

$f(x) = \begin{cases} x + 1, &x > 0\\\\\\\\ -2x + 2, &x < 0 \end{cases}$ -1.g.-

$\lim_{x \to 0^{+}} f(x) = 1 ≠ 2 = \lim_{x \to 0^{-}} f(x).$

$f(x) = \begin{cases} -x^{2} + 4, &x≤3\\\\\\\\ 4x - 8, &x > 3 \end{cases}$

$\lim_{x \to 3^{+}} f(x) = 4 ≠ -5 = \lim_{x \to 3^{-}} f(x).$

• A removable discontinuity occurs when the limit of a function $\lim_{x \to a}f(x) = L$ exists (the left-hand and right-hand limits at x = a are equal and finite), but f(a) is either undefined or not equal to that limit. The discontinuity could be removed (the hole in the graph could be filled) by redefining the function at that point to the limit, i.e., f(a) = L, e.g., f(x)=^sin(x)⁄_x -1.h-.   $\lim_{x \to 0} \frac{sin(x)}{x} = 1$, but f(0) is not defined. If we redefine f(0) = 1, the discontinuity is removed, and the function becomes continuous at x = 0.
  Graphically, it appears as a hole (open circle) on an otherwise smooth curve.

f(x) = $\frac{x^{2}-4}{x-2}$. $\lim_{x \to 2}\frac{x^{2}-4}{x-2} = \lim_{x \to 2}\frac{(x-2)(x+2)}{x-2} = \lim_{x \to 2} (x+2) = 4,$ but f(2) is undefined.

$f(x) = \begin{cases} 2x + 1, &x<1\\\\\\ 2, &x=1\\\\\\ -x + 4, &x > 1 \end{cases}$

$\lim_{x \to 1^{+}} f(x) = 3 = \lim_{x \to 1^{-}} f(x), but \lim_{x \to 1} f(x) = 3 ≠ 2 = f(1)$

• A function has an infinite discontinuity at x = a if the function grows without bound $\lim_{x \to a^{+}} f(x) = \pm\infty$ or $\lim_{x \to a^{-}} f(x) = \pm\infty$ (it occurs when at least one one-sided limit is ±∞). Examples:

y = $\frac{1}{x}$ -1.f.-, $\lim_{x \to 0^{+}} \frac{1}{x} = \infty$ and $\lim_{x \to 0^{-}} \frac{1}{x} = -\infty$

y = $\frac{x+2}{x+1}$, $\lim_{x \to -1^{+}} \frac{x+2}{x+1} = \infty$ and $\lim_{x \to -1^{-}} \frac{x+2}{x+1} = -\infty$

f(x) = $\frac{1}{(x-2)^2}, \lim_{x \to 2^{+}} \frac{1}{(x-2)^2}=\lim_{x \to 2^{-}} \frac{1}{(x-2)^2} = \infty$.

f(x) = $\tan(x), \lim_{x \to \frac{\pi}{2}^{-}}\tan(x) = \infty, \lim_{x \to \frac{\pi}{2}^{+}} \tan(x)= -\infty$

These correspond to vertical asymptotes.

• A mixed discontinuity is a discontinuity that occurs when one-sided limit fails to exist (not even as ±∞). An example is y = $sin(\frac{1}{x})$ as $x \to 0$ -1.i.- The function oscillates infinitely often between −1 and 1 near x = 0, preventing the limit from existing. Both one-sided limits do not exist (not even ±∞).

Exemplary cases

• Polynomials, sin(x), cos(x), exponential ($e^x, a^x$, a > 0), hyperbolic (sinh(x), cosh(x)) are continuous everywhere.
• tan(x) has discontinuities at odd multiples of π/2.
• The Dirichlet function is nowhere continuous, $f(x) = \begin{cases} 1, &x \in \mathbb{Q} \\\\ 0, &x \in \mathbb{R} \setminus \mathbb{Q} \end{cases}$. Every neighborhood of a contains both rationals and irrationals, so the Dirichlet function jumps between 0 and 1 infinitely often near any point, and $\lim_{x \to a}f(x)$ does not exist for any a.
• The Greatest Integer Function or floor function, [x], which gives the largest integer less than or equal to x has infinitely many discontinuities. At every integer $n \in \mathbb{Z},\lim_{x \to n^-} [x] = n-1, \lim_{x \to n^+} [x] = n$. Jump discontinuity of size 1 at each integer.

Differentiability implies continuity

Theorem. If a function f is differentiable at x = a, then f is continuous at x = a.

Proof. We need to check if $\lim_{x \to a} f(x) = f(a) ↔ \lim_{x \to a} f(x) - f(a) = 0$

$\lim_{x \to a} f(x) - f(a) = \lim_{x \to a} \frac {f(x) - f(a)}{x - a}(x-a) =$[By assumption, f’(a) exists and also $\lim_{x \to a}(x-a) = 0$] f’(a)·0 = 0.

The converse is not true. A function can be continuous but not differentiable, e.g., f(x)=∣x∣ is continuous at x = 0, but f’(0) does not exist.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.