|
 |
 |
|
|
|
|
It ain’t about how hard you can hit. Its about how hard you can get hit, and how much you can take, and keep moving forward, Rocky Balboa
Laurent’s theorem. Let A = {$z \in \mathbb{C}: R \lt |z -a| \lt S$} be an annular region ($0 \le R \lt S \le \infty$) and let f be analytic on A. Then, $f(z) = \sum_{n=-\infty}^\infty c_n(z -a)^n, \forall z \in A$ where $c_n = \frac{1}{2\pi i}\int_{\gamma} \frac{f(w)}{(w-a)^{n+1}}dw$ and $\gamma$ is a positively oriented circle of radius r centered at a and R < r < S ($\gamma$ is inside the annular region).
Corollary (aka Rosetta Stone of Complex Analysis). Let f be analytic in $\mathbb{B'}(a; r)$. (i) f has a removable singularity at a if and only if in the Laurent's series expansion of f around a ($\sum_{n = -\infty}^\infty (z-a)^n$) all negative coefficients are zero $c_n = 0, \forall n \lt 0$. (ii) f has a pole of order m ($m \ge 1$) at a if and only if the series stop at the negative power -m, $c_{-m} \ne 0, c_n = 0, \forall n \lt -m$; (iii) f has an isolated essential singularity at a if and only if the series has infinitely many negative terms (it never stops), i.e., there is no m such that $c_n = 0, \forall n \lt -m$
The Argument Principle. Suppose f is meromorphic on and inside a simple closed curve $\gamma$ with a finite number of zeroes $a_j, 1 \le j \le l_1$ and poles $b_k, 1 \le k \le l_2$. Suppose none of those zeros and poles lie on $\gamma$. Then, $\frac{1}{2\pi i}\int_{\gamma}\frac{f'(z)}{f(z)}dz = M - N$ where M is the sum of order of zeroes at $a_j, 1 \le j \le l_1$ and N is the sum of order of poles at $b_k, 1 \le k \le l_2$
We want to calculate the improper real integral: $\int_{0}^{\infty} \frac{dx}{1+x^{2n}}, \forall n \in \mathbb{N}, n \gt 1$. We cannot compute this directly using standard Calculus.
Inspired by this integral, we extend the integrand to the complex plane $\frac{1}{1+z^{2n}}$.
We choose a contour $\Gamma$ that consists of three paths (a “pizza slice”, Figure ii):
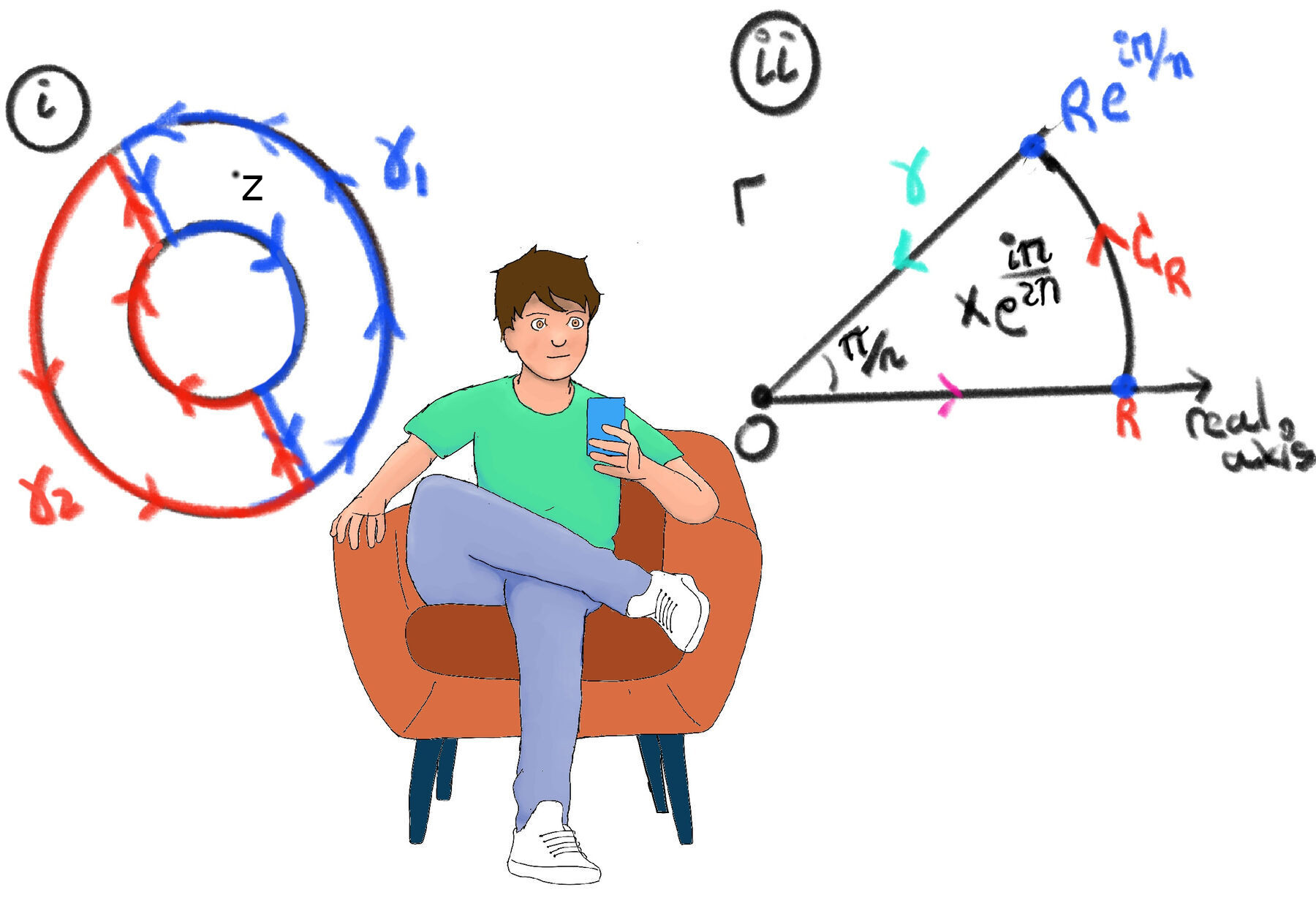
Why this specific angle $\pi/n$? Because the function depends on $z^{2n}$. If we rotate $z$ by an angle of $\pi/n$, then $z^{2n}$ rotates by $2n(\pi/n) = 2\pi$, which brings us back to where we started. This symmetry is absolutely essential for the algebra later.
We want to integrate $\frac{1}{1+z^{2n}}$ around our “Pizza Slice” shape (sector) in the complex plane. We need to find the singularities inside our pizza slice. Singularities occur when the denominator is zero: $1 + z^{2n} = 0 \implies z^{2n} = -1$. In polar form, $-1 = e^{i\pi}, e^{3i\pi}, e^{5i\pi}, \dots$. In polar form, all representations of -1 are $-1=e^{i(\pi +2\pi m)}, m\in \mathbb{Z}$. So, we solve $z^{2n}=e^{i(\pi +2\pi m)}$, the 2n distinct roots are: $z_k = e^{i\frac{(2k+1)\pi}{2n}}, k = 0, 1, 2, \cdots, 2n-1$.
Which one is inside our “pizza” 🍕 slice? Our slice goes from angle $0$ to $\frac{\pi}{n}$ (or $\frac{2\pi}{2n}$).
By Cauchy Residue Theorem, $\int_{\Gamma} \frac{1}{1+z^{2n} }dz= 2\pi i \cdot Res\{ \frac{1}{1+z^{2n}}; e^{\frac{i\pi}{2n}} \}$
$\lim_{z \to e^{\frac{i\pi}{2n}}} (z - e^{\frac{i\pi}{2n}}) \frac{1}{1+z^{2n}} =[\text{For simplicity, let's name }a = e^{\frac{i\pi}{2n}}] \lim_{z \to a} \frac{1}{\frac{1+z^{2n}-0}{z-a}}$
Recall the concept of derivative $g'(a) = \lim_{z \to a}\frac{g(z)-g(a)}{z-a}$ where $g(z) = 1 + z^{2n}, g (a) = 0$
We need the residue at $a = e^{i\frac{\pi}{2n}}$.Since it is a simple pole, we use the derivative formula: $\text{Res}(f, a) = \frac{1}{g'(a)} \quad \text{where } g(z) = 1+z^{2n}$
$lim_{z \to a} \frac{1}{\frac{1+z^{2n}-0}{z-a}} = \frac{1}{(1+z^{2n})'|_{e^{\frac{i\pi}{2n}}}} = \frac{1}{2nz^{2n-1}|_{e^{\frac{i\pi}{2n}}}} = \frac{1}{2n(e^{i\pi}e^{\frac{-i\pi}{2n}})} = \frac{e^{\frac{i\pi}{2n}}}{-2n} =\frac{-e^{\frac{i\pi}{2n}}}{2n}$
$2\pi iRes\{ \frac{1}{1+z^{2n}}; e^{\frac{i\pi}{2n}} \} = 2\pi i( \frac{-e^{\frac{i\pi}{2n}}}{2n}) = \frac{-i\pi e^{\frac{i\pi}{2n}}}{n}$
Now we break the loop into its three parts: $\int_{\Gamma} \frac{1}{1+z^{2n}}dz = \int_{0}^{R}\frac{1}{1+x^{2n}}dx + \int_{C_R}\frac{1}{1+z^{2n}}dz + \int_{\gamma}\frac{1}{1+z^{2n}}dz$.
$z = r e^{i\frac{\pi}{n}} \implies dz = e^{i\frac{\pi}{n}} dr$. Then, $1 + z^{2n} = 1 + (r e^{i\frac{\pi}{n}})^{2n} = 1 + r^{2n} e^{i 2\pi} = 1 + r^{2n}$ (The avid reader should not fail to notice how the complex part has completely vanished! This is why we chose this angle and “pizza slice”).
$\int_{\gamma} \frac{dz}{1+z^{2n}} = \int_{R}^{0} \frac{e^{\frac{i\pi}{n}}dr}{1+ (re^{\frac{i\pi}{n}})^{2n}} = -e^{\frac{i\pi}{n}}\int_{0}^{R} \frac{dr}{1+r^{2n}}$ Letting $R \to \infty$, this becomes $-e^{\frac{i\pi}{n}}\int_{0}^{\infty} \frac{dx}{1+x^{2n}} = - e^{i\frac{\pi}{n}} \cdot I$.
L.H.S. = $(1 -e^{\frac{i\pi}{n}})I = (1 -e^{\frac{i\pi}{n}})\int_{0}^{\infty} \frac{dx}{1+x^{2n}}$
R.H.S. = $\frac{-i\pi e^{\frac{i\pi}{2n}}}{n}$
Combining both results: $I = \frac{-\frac{i \pi}{n} e^{i\frac{\pi}{2n}}}{1 - e^{i\frac{\pi}{n}}}$
Multiply the numerator and denominator by $e^{-i\frac{\pi}{2n}}$: $I = \frac{-\frac{i \pi}{n} e^{i\frac{\pi}{2n}} \cdot e^{-i\frac{\pi}{2n}}}{(1 - e^{i\frac{\pi}{n}}) \cdot e^{-i\frac{\pi}{2n}}} = \frac{-\frac{i \pi}{n}}{e^{-i\frac{\pi}{2n}} - e^{i\frac{\pi}{2n}}}$
Swap the sign in the denominator to make it look like sine definition ($e^{ix} - e^{-ix}$), recall $\sin(\theta) = \frac{e^{i\theta} - e^{-i\theta}}{2i} \implies e^{i\theta} - e^{-i\theta} = 2i \sin(\theta)$: $I = \frac{-\frac{i \pi}{n}}{-(e^{i\frac{\pi}{2n}} - e^{-i\frac{\pi}{2n}})} = \frac{\frac{i \pi}{n}}{e^{i\frac{\pi}{2n}} - e^{-i\frac{\pi}{2n}}}= \frac{i \pi / n}{2i \sin(\frac{\pi}{2n})} = \frac{\pi}{2n \sin(\frac{\pi}{2n})}$
$\int_{0}^{\infty} \frac{dx}{1+x^{2n}} = \boxed{\frac{\pi}{2n \sin(\frac{\pi}{2n})}}$
Use a residue and the following contour $\gamma_R$ to show that $\int_{0}^{\infty} \frac{dx}{x^3+1} = \frac{2\pi}{3\sqrt{3}}$
Solution:
We want to calculate $I = \int_{0}^{\infty} \frac{dx}{x^3+1}$. We choose a “Pizza Slice” contour (sector) $\Gamma_R$ in the complex plane to exploit the symmetry of $z^3$.
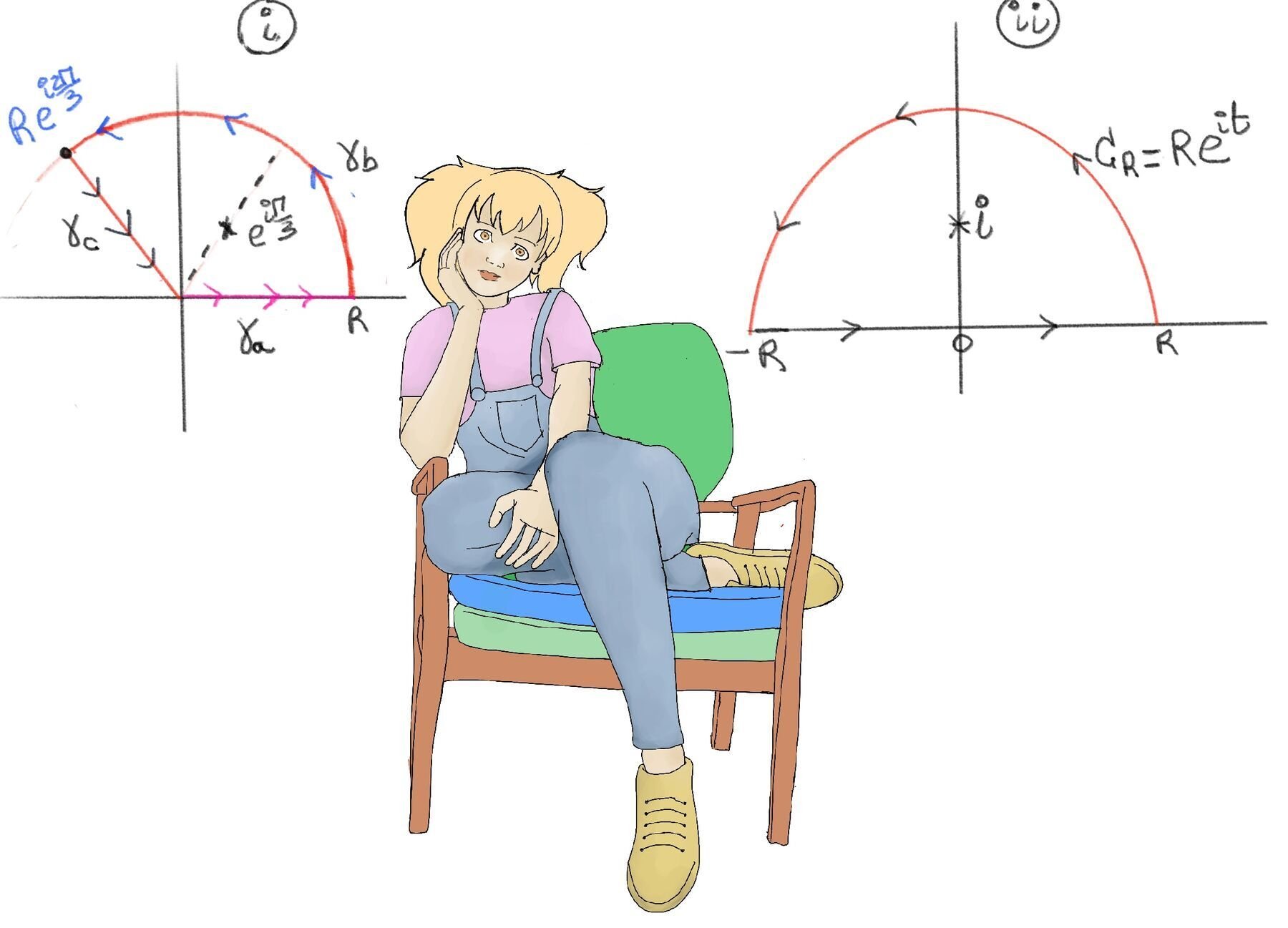
$\gamma$ can be sliced into three parts as follows (Figure i):
Inspired by the integrand of the problem, we define the complex function $f(z) = \frac{1}{z^3+1}$. We need to calculate the roots of $z^3 + 1 = 0 \implies z^3 = -1$. In polar form, $-1 = e^{i\pi}$.
The roots are separated by $2\pi/3: z = e^{\frac{2n\pi + \pi}{3}i}$ for n = 0, 1, and 2. $z_0 = e^{\frac{i\pi}{3}}$ (n = 0, Angle $60^\circ$), $z_1 = e^{i3\pi/3} = e^{i\pi} = -1$ (n = 1, Angle $180^\circ$), and $z_2 = e^{i5\pi/3}$ (n = 2, Angle $300^\circ$).
Our slice goes from $0^\circ$ to $120^\circ$ ($2\pi/3$), therefore only $z_0 = e^{i\pi/3}$ lies inside the contour.
The residue at a simple pole $z_0$ for $f(z) = 1/g(z)$ is the derivative formula: $\text{Res} = 1/g'(z_0)$. In our particular case, $g(z) = z^3 + 1 \implies g'(z) = 3z^2$, and evaluated at $z_0 = e^{i\pi/3}$ gives $\text{Res}(f, e^{i\pi/3}) = \frac{1}{3(e^{i\pi/3})^2} = \frac{1}{3e^{i2\pi/3}} = \frac{e^{-i2\pi/3}}{3} = \frac{1}{3} \left( \cos\left(-\frac{2\pi}{3}\right) + i\sin\left(-\frac{2\pi}{3}\right) \right) = \frac{1}{3} \left( -\frac{1}{2} - i\frac{\sqrt{3}}{2} \right)$
By Cauchy’s residue theorem, $\int_{\gamma_R} f(z)dz = 2\pi i Res(f, e^{\frac{i\pi}{3}})$ (*)
$\int_{\gamma_R} f(z)dz = \int_{\gamma_a} f(z)dz =\int_{\gamma_b} f(z)dz = \int_{\gamma_c} f(z)dz$
Analyzing the Three Paths:
Path $\gamma_a$ (Real Axis): $\int_0^R \frac{dx}{x^3+1} \to I \quad (\text{as } R \to \infty)$
Path $\gamma_b$ (The Arc): $\gamma_b(t) = Re^{it}, 0 \le t \le \frac{2\pi}{3}$. $z=Re^{it},\ dz=iRe^{it}dt, |dz|=Rdt$. $\int_{\gamma_b} f(z)dz = \int_{0}^{\frac{2\pi}{3}}\frac{Re^{it}idt}{R^3e^{i3t} + 1}$
Notice that $e^{3it}$ is a point in the unit circle, so $R^3e^{i3t}$ is in the circle of radius $R^3, |R^3e^{i3t} + 1| \ge[\text{Reverse triangle inequality} |z+w| ≥ ∣z∣−∣w|] R^3-1$. Hence, $\frac{1}{|R^3e^{i3t} + 1|} \le \frac{1}{R^3-1}$
$|\int_{0}^{\frac{2\pi}{3}}\frac{Re^{it}idt}{R^3e^{i3t} + 1}| \le R\int_{0}^{\frac{2\pi}{3}} \frac{|dt|}{|R^3e^{i3t} + 1|}$
$R\int_{0}^{\frac{2\pi}{3}} \frac{|dt|}{|R^3e^{i3t} + 1|} \le \frac{R}{R^3-1}\cdot \frac{2\pi}{3} = \frac{2\pi}{3}\frac{R}{R^3-1} \to 0 \text{ as } R \to \infty$
Path $\gamma_c$ (The Return Trip): We travel from $Re^{i2\pi/3}$ to $0$. Let parameterize it using $z = t e^{i2\pi/3}, R \ge t \ge 0$. $z^3 = (t e^{i2\pi/3})^3 = t^3 e^{i2\pi} = t^3, dz = e^{i2\pi/3} dt$
$\int_{\gamma_c} f(z)dz = \int_R^0 \frac{e^{\frac{2\pi}{3}}dt}{(e^{\frac{2\pi}{3}}t)^3+1} = - e^{i2\pi/3} \int_0^R \frac{dt}{t^3+1}$. As $R \to \infty$: $\int_{\gamma_c} f(z)dz \to - e^{i2\pi/3} I$
By Cauchy’s residue theorem (*): $I + 0 - e^{i2\pi/3} I = 2\pi i \left( \frac{1}{3e^{i2\pi/3}} \right)$
Factor out $I$: $I (1 - e^{i2\pi/3}) = \frac{2\pi i}{3e^{i2\pi/3}}$
Solve for $I$:
$$ \begin{aligned} I &=\frac{2\pi i}{3e^{i2\pi/3} (1 - e^{i2\pi/3})} \\[2pt] &= \frac{2\pi i}{3 (e^{i2\pi/3} - e^{i4\pi/3})}\\[2pt] &[\text{Use periodicity of the complex exponential: } e^{i4\pi/3} = e^{i4\pi/3 -2\pi} = e^{i4\pi/3 -6\pi/3} = e^{-i2\pi/3}] \\[2pt] &= \frac{2\pi i}{3(e^{i2\pi/3} - e^{-i2\pi/3})} \\[2pt] &[\text{Recall the identity: } e^{i\theta}-e^{-i\theta}=2i\sin(\theta)] \\[2pt] &= \frac{2\pi i}{3 (2i \sin(2\pi/3))} \\[2pt] &= \frac{\pi}{3 \sin(2\pi/3)} \\[2pt] &[\text{We know }] sin(\frac{2\pi}{3}) = \frac{\sqrt{3}}{2} \\[2pt] &=\frac{\pi}{3 (\frac{\sqrt{3}}{2})} = \frac{2\pi}{3\sqrt{3}} \end{aligned} $$The reader should notice that the integrand, $f(x) = \frac{\cos(3x)}{(x^2+1)^2}$ is an even function.
$\int_{-\infty}^\infty \frac{\cos(3x)}{(x^2+1)^2} =[\text{Improper integral definition}] \lim_{R_1 \to \infty} \int_{-R_1}^0 \frac{\cos(3x)}{(x^2+1)^2} + \lim_{R_2 \to \infty} \int_0^{R_2} \frac{\cos(3x)}{(x^2+1)^2}$
Define the complex function $f(z) := \frac{e^{i3z}}{(z^2+1)^2} = \frac{\cos(3z)}{(z^2+1)^2} + i \frac{\sin(3z)}{(z^2+1)^2}$.
Why not integrate just cos(3z)? If we put $\cos(3z)$ directly into the complex plane, it blows up (goes to infinity) along the imaginary axis because $\cos(iy) = \cosh(y)$. Instead, we use Euler’s formula: $e^{3ix} = \cos(3x) + i\sin(3x)$ and we will integrate the function $f(z) = \frac{e^{3iz}}{(z^2+1)^2}$
We integrate over a simple closed loop $\gamma$ consisting of two parts (Figure ii):
The denominator is $(z^2+1)^2 = 0$. Its roots are $z = i$ and $z = -i$. Since the denominator is squared, these are poles of order 2. Except in these poles, f is entire everywhere. Inside our upper semicircle contour, the only singularity is z = i.
By Cauchy’s residue theorem, $2\pi i Res(f; i) = \int_{\gamma + C_R} f(z)dz = \int_{\gamma} f(z)dz + \int_{C_R} f(z)dz$
For a pole of order 2 at $z_0$, the residue is: $\text{Res}(f, z_0) = \lim_{z \to z_0} \frac{d}{dz} \left[ (z-z_0)^2 f(z) \right]$
Multiply $f(z)$ by $(z-i)^2$ to remove the singularity: $\phi(z) = (z-i)^2 f(z) =[f(z) = \frac{e^{3iz}}{(z-i)^2(z+i)^2}] \frac{e^{3iz}}{(z+i)^2}$
We need $\phi'(z)$. Use the Quotient Rule $\left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2}$, $u = e^{3iz} \implies u' = 3ie^{3iz}, v = (z+i)^2 \implies v' = 2(z+i)$, we get: $\phi'(z) = \frac{3ie^{3iz}(z+i)^2 - e^{3iz} \cdot 2(z+i)}{((z+i)^2)^2} =[\text{Factor out } e^{3iz}(z+i)] \frac{e^{3iz}(z+i) [ 3i(z+i) - 2 ]}{(z+i)^4} = \frac{e^{3iz} [ 3iz - 3 - 2 ]}{(z+i)^3} = \frac{e^{3iz} (3iz - 5)}{(z+i)^3}$
$Res(f, i) = \frac{e^{3iz} (3iz - 5)}{(z+i)^3}|_{z=i} = \frac{e^{3i(i)}(3i(i) - 5)}{(i + i)^3} = \frac{e^{-3} (-3 - 5)}{(2i)^3} = \frac{-8e^{-3}}{-8i} = \frac{ 8e^{-3}}{8i^3} = \frac{e^{-3}}{i} =\frac{-i}{e^3}$
Cauchy’s Residue Theorem, $\oint_\gamma f(z) dz = 2\pi i \left( \frac{-i}{e^3} \right) = \frac{2\pi (-i^2)}{e^3} = \frac{2\pi (1)}{e^3} = \frac{2\pi}{e^3}$
This gives us the value for the entire closed loop: $\int_{-R}^R f(x) dx + \int_{C_R} f(z) dz = \frac{2\pi}{e^3}$
The Arc Integral vanishes. $z = Re^{it}, dz = Rie^{it}dt, f(z) = \frac{e^{3iRe^{it}}}{(R^2e^{2it}+1)^2}$
The integral around $C_R$ is the following expression: $\int_{0}^\pi \frac{e^{3iRe^{it}}Rie^{it}dt}{(R^2e^{2it}+1)^2}$
Notice that $e^{2it}$ is a point in the unit circle, so $R^2e^{i2t}$ is in the circle of radius $R^2, |R^2e^{i2t} + 1| \ge[\text{Reverse triangle inequality} |z+w| ≥ ∣z∣−∣w|] R^2-1$. Hence, $\frac{1}{(R^2e^{i2t} + 1)^2} \le \frac{1}{(R^2-1)^2}$
$e^{it}=\cos(t) + i\sin(t) \implies 3iRe^{it}=3iR\cos(t) - 3R\sin(t)$. This expression is complex, with real part $- 3R\sin(t)$, the modulus is $|e^{3iRe^{it}}| = e^{-3Rsin(t)} \le e^0 = 1 \iff -3R\sin(t)\le 0 \text{ i.e., } R \sin(t) \ge 0$ and this holds because R > 0 and t∈ [0,π] (where sin(t) ≥ 0, we are in the upper half plane).
$|\int_{0}^\pi \frac{e^{3iRe^{it}}Rie^{it}dt}{(R^2e^{2it}+1)^2}| \le |\int_{0}^\pi \frac{1\cdot R \cdot |dt|}{(R^2-1)^2} = \frac{R}{(R^2-1)^2}\cdot \pi \to 0 \text{ as } R \to \infty$.
In conclusion, taking the limit as $R \to \infty: \int_{-\infty}^\infty \frac{e^{3ix}}{(x^2+1)^2} dx + 0 = \frac{2\pi}{e^3}$
Next, we will separate real and imaginary parts: $\int_{-\infty}^\infty \frac{\cos(3x)}{(x^2+1)^2} dx + i \int_{-\infty}^\infty \frac{\sin(3x)}{(x^2+1)^2} dx = \frac{2\pi}{e^3} + 0i$
Finally, we equal both real parts and obtain: $\int_{-\infty}^\infty \frac{\cos(3x)}{(x^2+1)^2} dx = \frac{2\pi}{e^3}$
JustToThePoint Copyright © 2011 - 2026 Anawim. ALL RIGHTS RESERVED. Bilingual e-books, articles, and videos to help your child and your entire family succeed, develop a healthy lifestyle, and have a lot of fun. Social Issues, Join us.
This website uses cookies to improve your navigation experience.
By continuing, you are consenting to our use of cookies, in accordance with our Cookies Policy and Website Terms and Conditions of use.