The Winding Number of a Curve: A Comprehensive Guide

Silence is a source of great strength, Lao Tzu

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

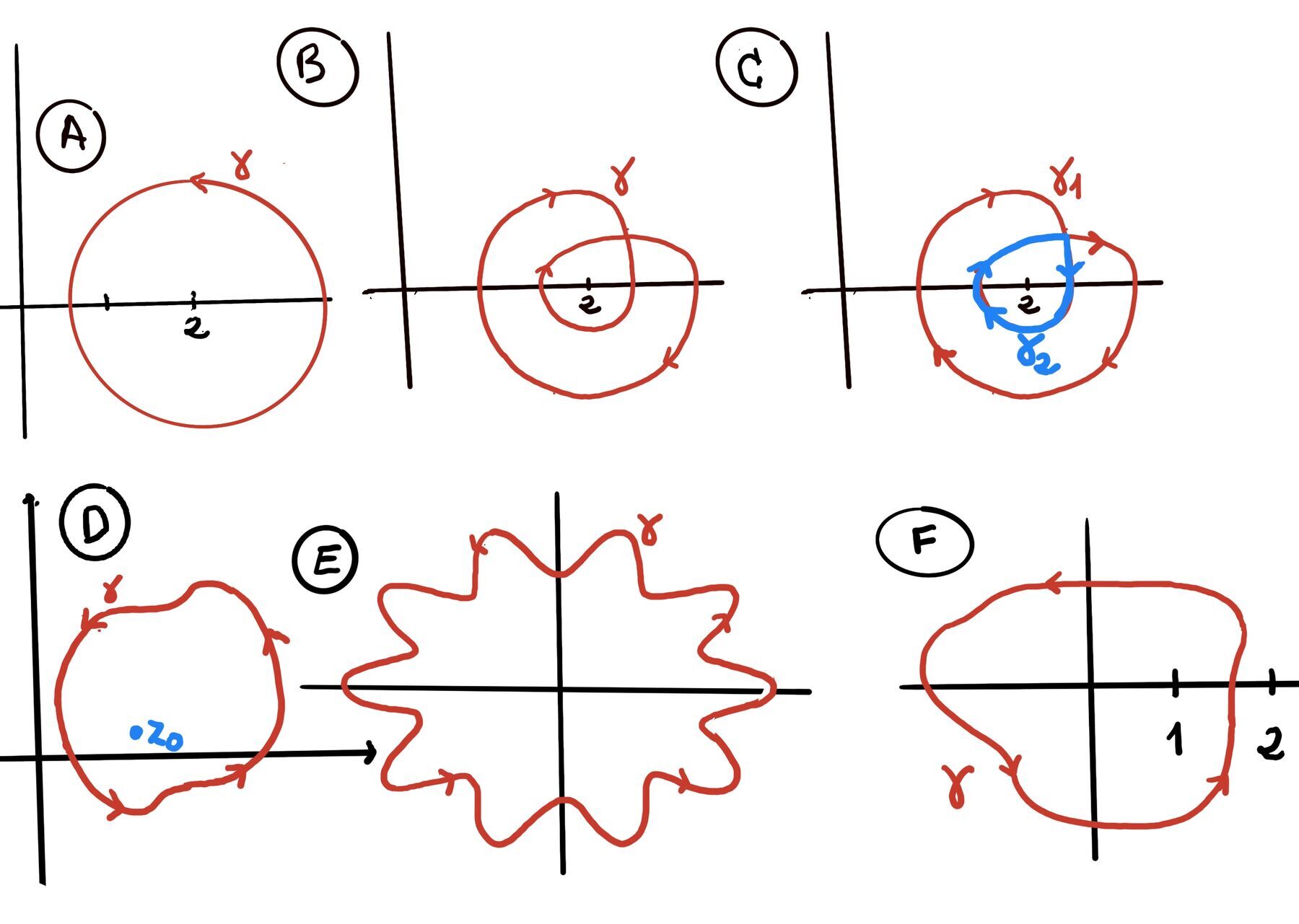
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

The Winding Number of a Curve

Lemma. If γ is a piecewise differentiable closed curve that does not pass through a point a in the complex plane, then the value of the integral $\oint_{\gamma} \frac{dz}{z-a}$ is an integer multiple of 2πi.

This Lemma proves that the integral $\oint_{\gamma} \frac{dz}{z-a}$ can only take on a discrete set of values: $\{ \dots, -2\pi i, 0, 2\pi i, 4\pi i, \dots \}$.

Proof.

Let the closed contour $\gamma$ be parameterized by $z = \gamma(t)$ for $t \in [\alpha, \beta]$. Since $\gamma$ is closed, the starting point $\gamma(\alpha)$ equals the final point $\gamma(\beta), \gamma(\alpha) = \gamma(\beta)$.

We define the function $h(t)$ as the value of the integral along the path $\gamma$ from the starting time $\alpha$ up to t: $h(t) = \int_{\alpha}^t \frac{\gamma'(u) du}{\gamma(u)-a} \text{ for } t \in [\alpha, \beta]$.

1. Since $\gamma$ is piecewise differentiable (continuous everywhere on $[\alpha, \beta]$ except possibly at a finite number of points) and $\gamma(t) \neq a$ (the path doesn’t pass through the singularity a), the denominator $\gamma(u) - a$ is never zero on the entire integration path, ensuring the denominator is bounded away from zero ($\gamma$ is a continuous curve on a compact interval $[\alpha, \beta], \gamma(u) - a$ is a non-zero continuous function), hence the resulting integrand is piecewise continuous on the compact interval $[\alpha, \beta]$ and then, the integral that defines h(t) is a proper Riemann integral (or a standard contour integral), which means it exists and is unique for every t, i.e., h(t) is well-defined. $h(t)$ is also a continuous function on $[\alpha, \beta]$.

   $h(t) = \int_{\alpha}^t f(u) du \quad \text{where } f(u) = \frac{\gamma'(u)}{\gamma(u)-a}$. A fundamental theorem of calculus states that if $f(u)$ is piecewise continuous on a closed interval $[\alpha, \beta]$, then the integral function $h(t)$ is continuous on that entire interval. Notice that h(t) represents the accumulated area as t increases. A piecewise continuous function f(u) can have a finite number of jumps. Integrating a finite jump results in a corner in the graph of the integral function h(t), but it does not result in a break or jump in h(t). For h(t) to be discontinuous, the integrand f(u) would have to contain an infinite singularity (which is ruled out because $\gamma(u) \neq a$).

2. At the start of the path, $h(\alpha) = \int_{\alpha}^\alpha \frac{\gamma'(u) du}{\gamma(u)-a} = 0$.
3. By the Fundamental Theorem of Calculus (for the real variable $t$), the derivative of $h(t)$ with respect to $t$ is the integrand evaluated at t: $h'(t) = \frac{\gamma'(t)}{\gamma(t)-a}$

Consider the auxiliary function $G(t) = e^{-h(t)} (\gamma(t)-a)$. We compute the derivative of $G(t)$ with respect to t.

$$ \begin{aligned} \frac{d}{dt}(e^{-h(t)} (\gamma(t)-a)) = & [\text{ Product rule: } \frac{d}{dt}(uv) = u'v + uv'] \\[2pt] &=e^{-h(t)}(-h'(t))(\gamma(t)-a) + e^{-h(t)}(\gamma'(t)) \\[2pt] &= [\text{Now, we substitute the expression for $h'(t)$ from (3)}] \\[2pt] &=e^{-h(t)}(-\frac{\gamma'(t)}{\gamma(t)-a})(\gamma(t)-a) + e^{-h(t)}(\gamma'(t)) \\[2pt] &=e^{-h(t)}(-\gamma'(t))+ e^{-h(t)}(\gamma'(t))\\[2pt] &=0. \end{aligned} $$

Since the derivative of the function $G(t)$ is identically zero on the interval $[\alpha, \beta]$, the function itself must be a constant, $e^{-h(t)} (\gamma(t)-a) = c$ where c is a constant.

This can be rearranged to express the path $\gamma(t)$ in terms of h(t): $\gamma(t)-a = ce^{h(t)}$. In particular, we evaluate the expression at $t = \beta, ce^{h(\beta)} = \gamma(\beta)-a = \gamma(\alpha) - a =[\text{Evaluating the expression at } t = \alpha] ce^{h(\alpha)} =[(2)] ce^0 = c$.

Since we know $h(\alpha) = 0$ (2), and $e^0 = 1:c(1) = \gamma(\alpha) - a \implies c = \gamma(\alpha) - a$. Since the curve does not pass through a, $c = \gamma(\alpha) - a \neq 0$.

Therefore, $ce^{h(\beta)} = c \leadsto[c \neq 0, \text{ we can divide both sides by c}] e^{h(\beta)} = 1 \leadsto h(\beta) = 2\pi i n$ for some integer n.

The solution to the equation $e^w = 1$ in the complex plane is $w = 2\pi i n$, where n is any integer ($\dots, -2, -1, 0, 1, 2, \dots$).

Finally, we observe that the value $h(\beta)$ is the desired integral: $\oint_{\gamma} \frac{dz}{z-a} = \int_{\alpha}^{\beta} \frac{\gamma'(t) dt}{\gamma(t)-a} = h(\beta) = 2\pi i n$

Definition. Suppose we are given a closed, oriented curve in the xy plane. Then, the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin.

When counting the total number of turns, counterclockwise motion counts as positive (it contributes +1 per full loop), while clockwise motion counts as negative (it contributes −1 per full loo).

Formal definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$.

Figure 4 illustrates indices −2, −1, 0, 1, 2, 3 for concentric loops with various orientations; the multi-loop picture shows different points $z_0, z_1, z_2$ with different winding counts.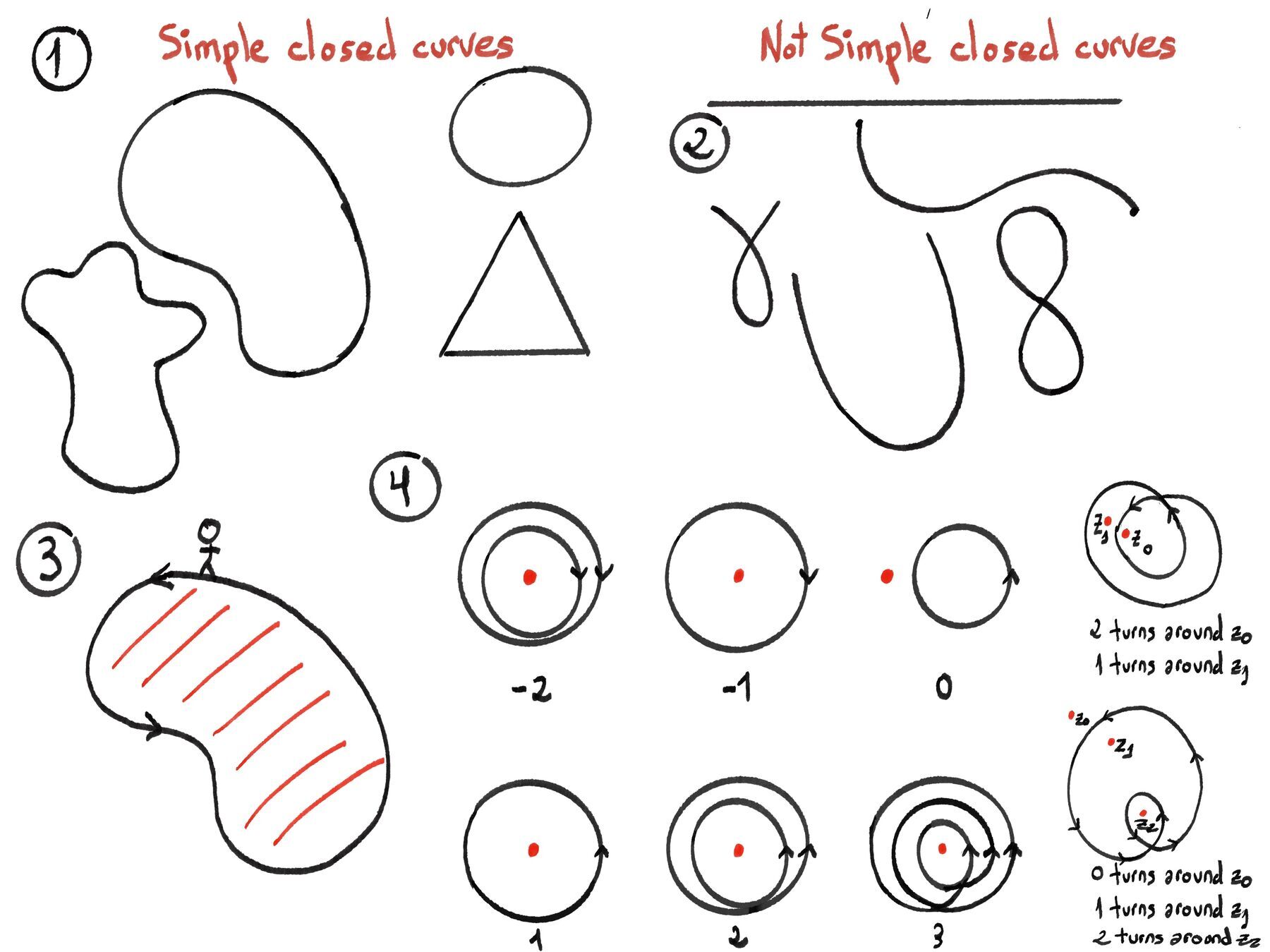

Key insight

• The integrand $\frac{1}{z-z_0}$ is analytic everywhere except at $z = z_0$.
• Imagine a circle around cero and then walk counterclockwise around that zero, hence we count one turn around that point, which means the winding number should be one. The integral measures how much the curve “encloses” the singularity at $z_0$, 2π (at the end we have completed a full rotation). $\oint_\gamma \frac{1}{z} = \begin{cases} 2\pi i, &\gamma: [0, 2\pi] → \mathbb{C}, t → e^{it} \\\\ 4\pi i, &\gamma: [0, 4\pi] → \mathbb{C}, t → e^{it} \\\\ 0, &\gamma: [a, b] → \mathbb{C} \end{cases}$ (last case) with image in a disk where 0 ∉ disk.
• The factor $\frac{1}{2\pi i}$ normalizes the result to an integer.
• The winding number is essentially the total change in the polar angle (argument) of $z −z_0$ as z traverses the curve once, divided by 2π.

To understand why this formula works, consider the polar representation. Write: $z-z_0 = re^{i\theta} \leadsto dz = e^{i\theta}dr + ire^{i\theta}d\theta \leadsto \frac{dz}{z-z_0} = \frac{e^{i\theta}dr + ire^{i\theta}d\theta}{re^{i\theta}} = \frac{dr}{r}+id\theta$

$\oint_{\gamma} \frac{dz}{z - z_0} = \int_a^b \frac{dr}{r}+id\theta = ln(r)\bigg|_{a}^{b} + i×\text{total change in θ}$

The term $\frac{dr}{r}$ integrates to zero because ln(r) returns to its initial value (closed curve).

$\oint_{\gamma} \frac{dz}{z - z_0} = i×\text{total change in θ} = i(2\pi k)$ where k is the net number of revolutions. Dividing by 2πi gives k, the winding number.

Relation to Jordan Curve Theorem

For a simple closed curve γ:

• $n(\gamma; z_0) \in \mathbb{Z}$ and is constant on each connected component of $\mathbb{C} \setminus \gamma$. In other words, the winding number is constant for all points within a connected region defined by the curve. If $z_0$ is in the bounded interior of γ, the curve wraps around it exactly once, $∣n(\gamma), z_0| = 1$. The sign of the winding number depends on the curve’s orientation: The sign is positive if γ is positively oriented (counterclockwise), negative if negatively oriented.
• If $z_0$ is in the unbounded exterior of γ, the curve does not enclose it at all, $n(\gamma, z_0) = 0$.

  This is intuitive: if you are standing far away from a loop, your total change of argument θ as someone walks around it is zero —they return to their starting position without ever circling you.

• The winding number provides a perfect mathematical test to determine if a point is inside or outside a simple closed curve. If $n(\gamma; z_0) \ne 0$, the point is inside; if $n(\gamma; z_0) = 0$, the point is outside.
• Homotopy invariance in the complement: if $\gamma_1$ and $\gamma_2$ can be deformed into each other without ever crossing the point $z_0$, then their winding numbers around $z_0$ will be identical, $n(\gamma_1; z_0) = n(\gamma_2; z_0)$.

  This means you can replace a complicated curve with a simple one (like a circle) for calculation purposes, provided the new curve encloses the same points.

• Additivity: If you have a path γ composed of two loops, $\gamma_1$ and $\gamma_2$, the total winding number is the sum of the individual winding numbers: $n(\gamma_1 + \gamma_2; z_0) = n(\gamma_1; z_0) + n(\gamma_2; z_0)$.
• Reversal: Traversing a curve in the opposite direction negates the winding number: $n(-\gamma; z_0) = - n(\gamma; z_0)$.

Examples

• Circle Around the Origin. Let $ \gamma(t) = e^{i2\pi t} $ for $ t \in [0, 1] $. This traces the unit circle counterclockwise. The winding number around $z_0 = 0$ is:

$n(\gamma, 0) = \frac{1}{2\pi i} \int_{0}^{1} \frac{1}{e^{i2\pi t}} \cdot \frac{d}{dt}(e^{i2\pi t}) dt = \frac{1}{2\pi i} \int_{0}^{1} \frac{i2\pi e^{i2\pi t}}{e^{i2\pi t}} dt = \frac{1}{2\pi i} \cdot i2\pi = 1$

A circle centered at the origin with a point inside has a winding number of +1 (counterclockwise) or -1 (clockwise).

• Circle. Let $\gamma(t)=Re^{it}, 0 \le t \le 2\pi$. Then, $\gamma$ is a positively oriented Jordan curve.

For any $z_0$ with $|z_0| \lt R, \mathbb{n}(\gamma; z_0) = 1.$ This can be quickly verified using Cauchy’s Integral Formula. Let f(z)=1. The formula states: $\oint_\gamma \frac{f(z)}{z-z_0} dz = 2\pi i \cdot f(z_0)$. Substituting into the winding number definition: $\mathbb{n}(\gamma;z_0) = \frac{1}{2\pi i}\oint_\gamma \frac{f(z)}{z-z_0} dz = \frac{1}{2\pi i} (2\pi i \cdot f(z_0)) = f(z_0) = 1.$

For any $z_0$ with $|z_0| > R, \mathbb{n}(\gamma;z_0) = 0.$ This follows from Cauchy’s Theorem. If $z_0$ is outside the circle, the function f(z) = $\frac{1}{z-z_0}$ is analytic at all points inside and on the contour γ. Therefore, its integral over the closed contour is zero: $\mathbb{n}(\gamma;z_0) = \frac{1}{2\pi i}\oint_\gamma \frac{f(z)}{z-z_0} dz = \frac{1}{2\pi i} \cdot 0 = 0.$

Hence, $\mathbb{Int}(\gamma) = \{ z \in \mathbb{C} | \mathbb{n}(\gamma; z_0) = 1 \} = \{ z \in \mathbb{C} | |z| < R \} \text{ and } \mathbb{Ext}(\gamma) = = \{ z \in \mathbb{C} | \mathbb{n}(\gamma; z_0) = 0 \} = \{ z \in \mathbb{C} | |z| > R \}.$

• Simple polygon (one that does not self-intersect). Let γ be its boundary traversed counterclockwise. This is a perfect example of a Jordan curve. As such, the Jordan Curve Theorem guarantees that it cleanly separates the complex plane into two distinct regions: A bounded interior, which is the area inside the polygon $Int(\gamma^∘)$; an unbounded exterior, which is the area outside. For any $z_0 \in Int(\gamma^∘), n(\gamma; z_0) = 1$ (γ will encircle the point exactly once in the positive direction); for $z_0 \notin \bar{\mathbb{P}}, n(\gamma; z_0) = 0$ (the boundary does not wrap around it at all).

• Figure-Eight Curve. Let $ \gamma(t) = e^{i\pi t} + e^{i2\pi t} $, $ t \in [0, 2] $. This traces a figure-eight. The winding number around $ z_0 = 0 $ is undefined because the winding number is only defined for points that are not on the contour.

• Example of Cancellation. Consider a path made of two parts: γ₁, the unit circle traversed counter-clockwise, $e^{i2\pi t}$ for $ t \in [0, 1]$. The winding number around the origin is n(γ₁, 0) = 1, a full positive (counter-clockwise) loop around the origin; The unit circle traversed clockwise, $e^{-i2\pi t}$ for $ t \in [1, 2]$. The winding number around the origin is n(γ₂, 0) = -1, a full negative (clockwise) loop around the origin.

The total winding number of the combined path γ = γ₁​+γ₂ is the sum of the individual winding numbers: n(γ, 0) = n(γ₁, 0) + n(γ₂, 0) = 1 + (-1) = 0.

The two loops cancel each other out. The combined path γ winds around the origin zero times

• Let γ be any positively oriented Jordan curve. Then, for any $z_0 \notin \gamma, n(\gamma; z_0) = \begin{cases} 1, z_0 \in Int(\gamma) \\\\ 0, z_0 \in Ext(\gamma) \end{cases}$

Case 1. $z_0 \in Int(\gamma)$

1. Approximate the Curve with a Polygon. A Jordan curve γ can be approximated arbitrarily well by a simple polygon P that lies entirely within its interior. We can construct P to be positively oriented and “close enough” to γ so that it also contains $z_0$. Because the winding number integral is continuous with respect to the path, this approximation doesn’t change the result: $n(\gamma, z_0) = n(P, z_0)$

2. Triangulate the Polygon. Any simple polygon can be divided into a finite number of triangles ($T_1, T_2, \cdots T_k$). The integral over the boundary of the polygon is the sum of the integrals over the boundaries of these triangles. This is because all the internal edges are traversed twice in opposite directions, and their integrals cancel each other out, leaving only the integral over the exterior boundary: $n(P, z_0) = \sum_{j=1}^k n(∂T_j,z_0)$.

3. Isolate the Key Triangle. The point $z_0$ must lie in the interior of exactly one of these triangles, let’s call it $T_1$. For any other triangle $T_j, j \ne 1$, the point $z_0$ is in its exterior. The function $\frac{1}{z-z_0}$ is analytic inside and on the boundary of $T_j$. By Cauchy’s Integral Theorem, the integral is zero. Thus, $n(∂T_j,z_0) = 0$ for j ≠ 1.

   This means our sum collapses to a single term: $n(P, z_0) = \sum_{j=1}^k n(∂T_j,z_0) = n(∂T_1,z_0)$

4. Deform the Triangle to a Circle (Homotopy). Let C be a small, positively oriented circle centered at $z_0$ that lies completely inside the triangle $T_1$. The function $\frac{1}{z-z_0}$ is analytic in the region between the triangle’s boundary and the circle. By the Deformation Principle (homotopy invariance), we can continuously deform the triangular path $∂T_1$ into the circular path C without changing the value of the integral: $n(∂T_1,z_0) = n(C, z_0)$. The winding number of a positively oriented circle around its center is known to be 1, so $n(\gamma, z_0) = n(P, z_0) = \sum_{j=1}^k n(∂T_j,z_0) = n(∂T_1,z_0) = n(C, z_0) = 1.$

Case 2. $z_0 \in Ext(\gamma)$

If $z_0$ is in the unbounded exterior region, the function $f(z) = \frac{1}{z-z_0}$ is analytic at all points inside and on the contour γ. The singularity at $z_0$ is outside the domain enclosed by the curve. By Cauchy’s Integral Theorem, the integral of an analytic function over a simple closed contour is zero: $\oint_{\gamma} \frac{1}{z-z_0} = 0$. Therefore, the winding number is: $n(\gamma; z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{1}{z-z_0} = \frac{1}{2\pi i} \cdot 0 = 0.$