Cauchy's Theorem for Multiply Connected Domains

The only way to learn mathematics is to do mathematics, Paul Halmos

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

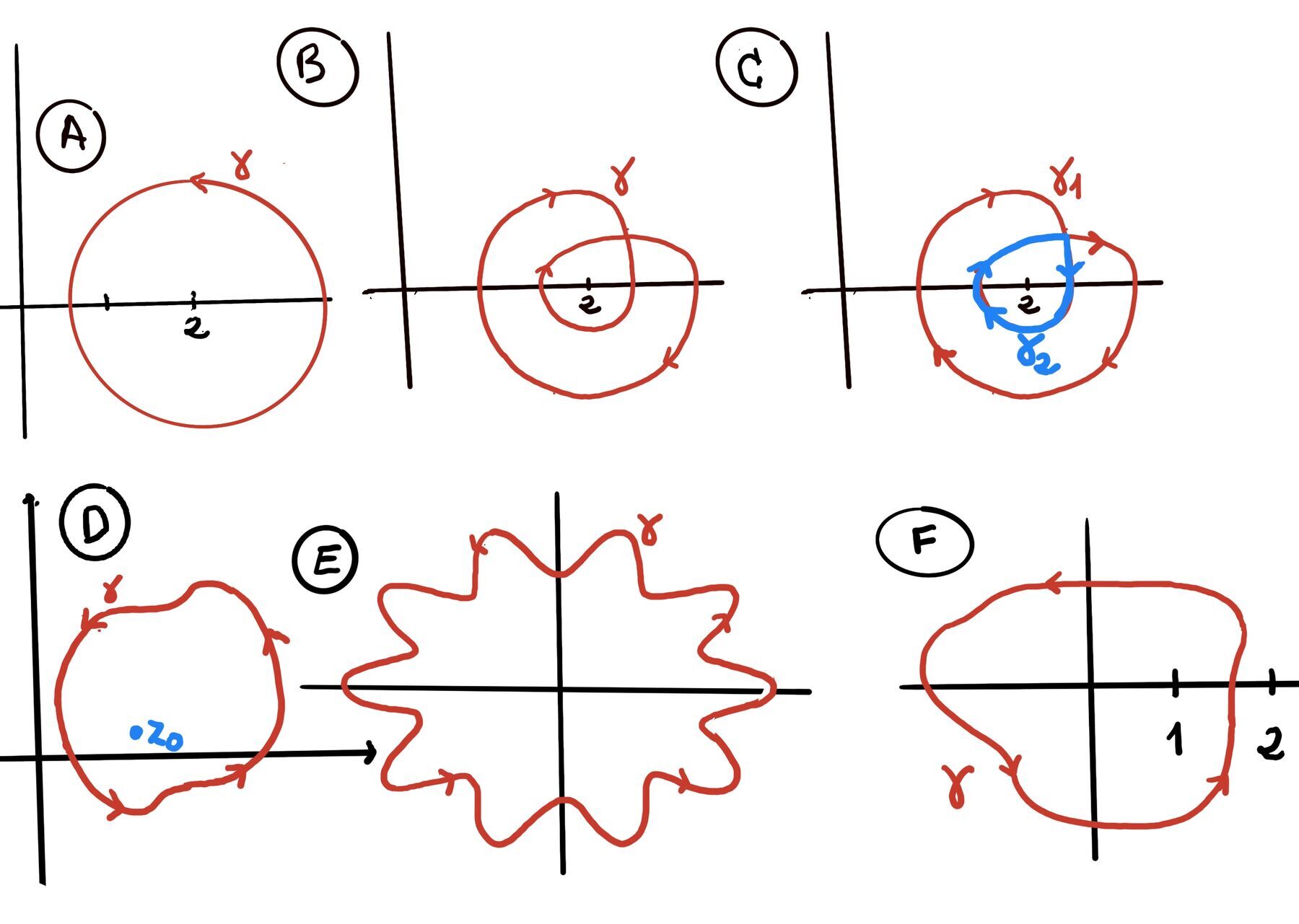
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

Cauchy’s Theorem for simply connected domains

Cauchy’s Theorem for simply connected domains. If a function f is analytic (a function that is complex-differentiable at every point within a domain, i.e., well-behaved and smooth, with no sharp corners, breaks, or singularities like division by zero) throughout a simply simple connected domain D then $\oint_C f(z)dz = 0$ for every closed contour C lying in D.

Cauchy’s Theorem for Multiply Connected Domains

Cauchy’s Theorem for a Multiply Connected Domain. Let C be a positively oriented (counterclockwise) simple closed contour. Let $C_1​, C_2​, \cdots, C_n$​ be positively oriented simple closed contours lying strictly inside C with pairwise disjoint interiors (they don’t overlap and no contour is inside another). Let $R$ be the multiply connected region (with n holes) inside $C$ but outside of every $C_k$ (each $C_k$ surrounds only one hole in the domain), $R = Int(C) \setminus \bigcup_{k=1}^n \overline{​Int(C_k​)}$​. If f(z) is analytic on an open set containing $\overline{R}$ (hence analytic on each boundary component $C, C_1, \ldots, C_n$), then: $\oint_C f(z)dz = \sum_{k=1}^n \oint_{C_k} f(z)dz$ where all contours ($C$ and every $C_k$) are traversed in the same direction (e.g., all counter-clockwise).

The integral over the outer boundary is equal to the sum of the integrals over the inner boundaries (the holes).

Proof:

The idea is to transform the multiply connected region $R$ into a simply connected region (Figure ii).

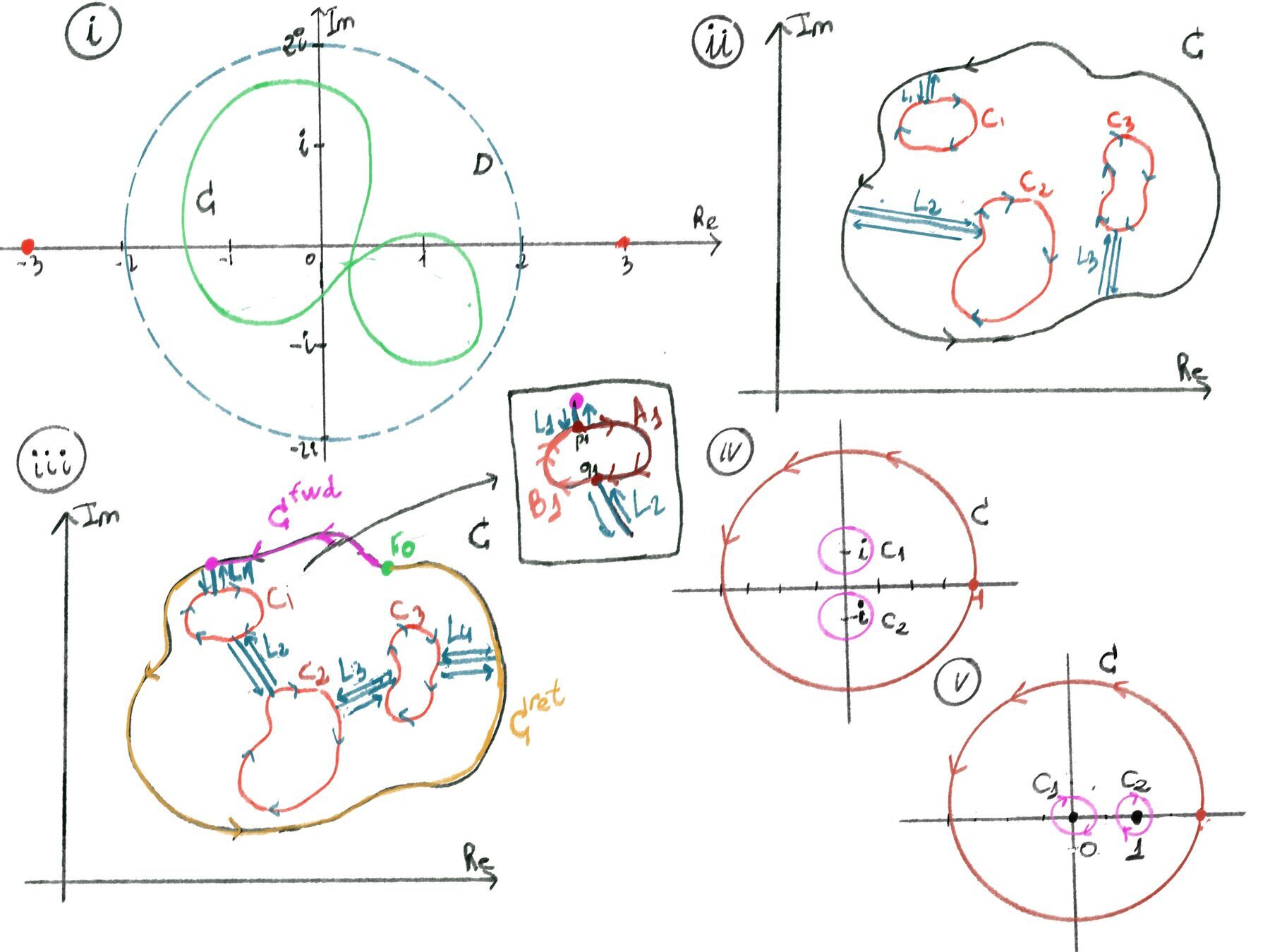
Imagine our region $R$ as a piece of paper with $n$ holes punched through it. A loop within this region cannot be contracted to a point if it surrounds a hole. To resolve this, we create a series of “cuts” or “bridges.” We will choose $n$ pairwise disjoint polygonal arcs (cuts), $L_k$, each one connecting the outer contour $C$ to one of the inner contours $C_k$. The arcs lie entirely in R except at their endpoints. The arcs are mutually disjoint and do not meet any boundary except at their endpoints.

Now, consider the region $R'$ formed by “cutting” $R$ along these lines, $R' = R \setminus \bigcup_{k=1}^n L_k$ This new region is simply connected. Why is that? Because any loop you could possibly draw in it can be shrunk to a point. If a loop attempts to encircle a hole, the “cut” prevents this by forcing it back, ensuring it cannot actually loop around the hole.

In other words, any loop that tries to wind around a hole is forced to cross its cut and thus cannot remain in R′.

Now that we have a simply connected region R’, let’s trace its entire boundary. We will create one single, continuous, non-intersecting (simple) contour, which we’ll call $\Gamma$.

Let’s trace $\Gamma$ so that the region $R'$ is always on our left side (“positive” orientation). Here is the path of $\Gamma$:

1. Start on C and go counterclockwise until you meet the first cut $L_1$.
2. When you get to the cut $L_1$, travel into the region, along $L_1$ inwards, from C to $C_1$.
3. When you reach $C_1$, go all the way around $C_1$ in the clockwise (CW) direction (this keeps the left-hand rule true because the hole is outside R’).
4. Travel out of the region and return to C along the cut $L_1$ (this path is $-L_1$, i.e., same cut, opposite direction).
5. Continue along C to $L_2$, repeat steps 2-4, and so on for k = 1, 2, …, n.

The resulting Γ is a single simple closed contour (the boundary of the simply connected region R′).

Our new region R’ is simply connected. Our function f(z) is analytic everywhere inside and on the boundary of R’ (since we only cut through $R$, where $f(z)$ was already analytic). Our new contour $\Gamma$ is the boundary of R’. By the standard Cauchy-Goursat theorem (for simple contours), the integral of $f(z)$ over this entire path $\Gamma$ must be zero: $\oint_{\Gamma} f(z)dz = 0$

Now, let’s write out what $\oint_{\Gamma} f(z)dz$ actually is. It’s the sum of all the pieces we traveled:

$$ \begin{aligned} \oint_{\Gamma} f(z)dz &=\oint_C f(z)dz \text{( The outer loop, CCW )} \\[2pt] &+\sum_{k=1}^n\Bigl(\int_{L_k} f(z)dz \text{ [The cut "in"] } + \oint_{C_k'} f(z)dz \text{ [The inner loop, clockwise] } + \int_{-L_k} f(z)dz \text{ [The cut "out"] } \Bigr). \end{aligned} $$

A fundamental property of contour integrals is that reversing the path negates the value, $\int_{-L_k} f(z)dz = - \int_{L_k} f(z)dz$, so each cut contributes zero. Hence, $0 = \oint_{\Gamma} f(z)dz = \oint_C f(z)dz + \sum_{k=1}^n\oint_{C_k'} f(z)dz \text{ clockwise}$

So, we have: $\oint_C f(z)dz + \sum_{k=1}^n \oint_{C_k'} f(z)dz = 0$ where $C$ is counter-clockwise (CCW) and all the $C_k'$ are clockwise (CW).

Let $C_k$ (without the prime) be the counter-clockwise (CCW) path around the $k$-th hole. By the path-reversal rule, $\oint_{C_k'} f(z)dz = - \oint_{C_k} f(z)dz$.

Now, substitute this into our previous equation: $\oint_C f(z)dz + \sum_{k=1}^n \left( - \oint_{C_k} f(z)dz \right) = 0$

Or alternatively,

$\oint_C f(z)dz = \sum_{k=1}^n \oint_{C_k} f(z)dz$

• Alternative “chain of cuts” variant (Figure iii). Instead of n separate cuts from C to each $C_k$, you can:

For each inner boundary $C_k$, let: $p_k$ be the endpoint of $L_k$ on $C_k$, $q_k$ be the endpoint of $L_{k+1}$ on $C_k$. Decompose $C_k$ (with clockwise orientation) into two subarcs: (i) $A_k$. the CW arc on $C_k$ from $p_k$ to $q_k$ (traversed on the forward pass); $B_k$, the CW complementary arc from $q_k$ back to $p_k$ (traversed on the return pass). Similarly, C (with CCW orientation) is split by the endpoints of $L_1$ and $L_{n+1}$ into two CCW arcs:

1. $C^{\mathrm{fwd}}$: from the base point $r_0 \in C$ to the endpoint of $L_1$.
2. $C^{\mathrm{ret}}$: the complementary CCW arc from the endpoint of $-L_1$ back to $r_0$.

Boundary $\Gamma=\partial R'$ with region on the left:

1. Along $C^{\mathrm{fwd}}$ from $r_0$ to the start of $L_1$.
2. Along $L_1$ (from C to $C_1$).
3. Along $A_1$ (CW subarc on $C_1$ from $p_1$ to $q_1$).
4. Along $L_2$ (from $C_1$ to $C_2$)
5. Along $A_2$ (CW subarc on $C_2$ from $p_2$ to $q_2$).
6. $\cdots$.
7. Along $L_n$ (from $C_{n-1}$ to $C_n$).
8. Along $A_n$ (CW subarc on $C_n$ from $p_n$ to $q_n$).
9. Along $L_{n+1}$ (from $C_n$ back to C).
10. Along $-L_{n+1}$ (from C down to $C_n$).
11. Along $B_n$ (CW complementary subarc on $C_n$ from $q_n$ back to $p_n$).
12. Along $-L_n$ (from $C_n$ to $C_{n-1}$).
13. Along $B_{n-1}$ (CW complementary subarc on $C_{n-1}$ from $q_{n-1}$ back to $p_{n-1}$).
14. $\cdots$.
15. Finally, along $-L_1$ (from $C_1$ back to $C$).
16. Then, along $C^{\mathrm{ret}}$ (CCW) to return to $r_0$.

This produces a single “stitch” that opens every hole. The boundary $\Gamma$ of the resulting simply connected region consists of C, each $C_k$ (clockwise), and the cuts $L_j$ (each used once forward and once backward). The same cancellation of the cut integrals yields exactly the same identity.

You don’t traverse each $C_k$ entirely on the forward pass. You take the CW subarc $A_k$ from where you enter $C_k$ via $L_k$ to where you leave it via $L_{k+1}$, and you finish the complementary CW subarc $B_k$ on the way back.

TL;DR. On the forward pass you traverse only the first half $A_k$ of each inner boundary (CW), then on the return pass you traverse the second half $B_k$ (also CW). Together they make the full clockwise loop $C_k$. All cut integrals cancel pairwise.

Examples

• Let a lie inside $C_1$ but not in any other hole and not in R. Take $f(z)=\dfrac{1}{z-a}$ (analytic on R). Then, $\oint_C \frac{dz}{z-a} = \sum_{k=1}^n \oint_{C_k} \frac{dz}{z-a} = \oint_{C_1} \frac{dz}{z-a} = 2\pi i$. Every other inner integral is 0.
• If C is a simple closed curve enclosing z = 0 and z = 1, then what is $\oint_C \frac{1}{z(z-1)}$ (Figure v).

Solution: The function is not analytic where the denominator is zero, so we have two simple poles at z = 0 and z = 1. $C$ is a simple closed contour (positively oriented) that encloses both singularities. The region $R$ inside $C$ but outside the singularities is a multiply connected domain (a region with two “holes”).

To apply this theorem, we can take small clockwise circles $C_1$ and $C_2$ around the points 0 and 1. This theorem states that the integral over the outer boundary C is equal to the sum of the integrals over the inner boundaries $C_1$ and $C_2$. We use partial fractions to simplify the integrand: $\frac{1}{z(z-1)} = \frac{1}{z-1} - \frac{1}{z}$.

Thus,

$$ \begin{aligned} \oint_C \frac{dz}{z(z-1)} &=[\text{The Cauchy Theorem for Multiply Connected Domains}] \\[2pt] &=\oint_{C_1} \frac{dz}{z(z-1)} + \oint_{C_2} \frac{dz}{z(z-1)} \\[2pt] &=\oint_{C_1}\frac{dz}{z-1} - \oint_{C_1}\frac{dz}{z} + \oint_{C_2}\frac{dz}{z-1} - \oint_{C_2}\frac{dz}{z}\\[2pt] &=0 - 2\pi i + 2\pi i - 0\\[2pt] &=0. \end{aligned} $$

$\oint_{C_1}\frac{dz}{z-1} = \oint_{C_2}\frac{dz}{z} = 0$ because we are integrating around $C_1$ and $C_2$, the circles around z = 0 and z = 1, respectively. The functions $\frac{dz}{z-1}$ and $\frac{dz}{z}$ are analytic everywhere inside $C_1$ and $C_2$ respectively, since their only singularities are at z = 1 and z = 0 respectively, which are obviously (they were chosen small circles) outside $C_1$ and $C_2$. By the Cauchy-Goursat Theorem, the integral of an analytic function over a simple closed contour is 0.

$\oint_{C_1}\frac{dz}{z} = 2\pi i$. We are integrating around $C_1$, which encloses the singularity at $z=0$. By the Cauchy Integral Formula (with $f(z)=1$ and $a=0$), this integral is $\oint_{C_1} \frac{dz}{z-0} = 2\pi i \cdot f(0) = 2\pi i \cdot 1 = \mathbf{2\pi i}$. Similarly, by the Cauchy Integral Formula with f(z) = 1 and $a=1, \oint_{C_2} \frac{dz}{z-1} = 2\pi i \cdot f(1) = 2\pi i \cdot 1 = \mathbf{2\pi i}$.

• Evaluate $\oint_C \frac{dz}{z²+1}$ where C is the circle |z| = 4 (Figure iv).

Solution: The function is not analytic where the denominator is zero, z²+1 = (z - i)(z + i) so we have two simple poles z = i and z = -i. C is a simple closed contour (positively oriented) that encloses both singularities. The region R inside C but outside the singularities is a multiply connected domain (a region with two “holes”).

To apply this theorem, we can take small clockwise circles $C_1$ and $C_2$ around the points i and -i. This theorem states that the integral over the outer boundary C is equal to the sum of the integrals over the inner boundaries ​$C_1$ and $C_2$. We use partial fractions to simplify the integrand: $\frac{1}{z²+1} = \frac{1}{2i}(\frac{1}{z-i}) - \frac{1}{2i}(\frac{1}{z+i})$.

Thus,

$$ \begin{aligned} \oint_C \frac{dz}{z²+1} &=[\text{The Cauchy Theorem for Multiply Connected Domains}] \\[2pt] &=\oint_{C_1} \frac{dz}{z²+1} + \oint_{C_2} \frac{dz}{z²+1} \\[2pt] &=\frac{1}{2i}\oint_{C_1}\frac{1}{z-i } - \frac{1}{2i}\oint_{C_1}\frac{1}{z+i} + \frac{1}{2i}\oint_{C_2}\frac{1}{z-i} - \frac{1}{2i}\oint_{C_2}\frac{1}{z+i}\\[2pt] &=\frac{1}{2i}(2\pi i) - 0 + 0 - \frac{1}{2i}(2\pi i)\\[2pt] &=\pi - \pi = 0. \end{aligned} $$

General Cauchy Theorem for Multiply Connected Domains

General Cauchy Theorem for Multiply Connected Domains. Let $R$ be the multiply connected region (with n holes) inside $C$ but outside of every $C_k$ (each $C_k$ surrounds only one hole in the domain), $R = Int(C) \setminus \bigcup_{k=1}^n \overline{​Int(C_k​)}$​, and let $f(z)$ be analytic on $R$. Now, let $\Gamma$ be any general closed contour (not necessarily simple) that lies entirely in R. This $\Gamma$ can wind around the “holes” (the regions inside each $C_k$) in any way it likes (this is the winding number or index of $\Gamma$ around each hole), the integral over $\Gamma$ is: $\oint_{\Gamma} f(z)dz = \sum_{k=1}^n m_k \oint_{C_k} f(z)dz$.

Definition. Let $a_k$ be any point inside the $k$-th hole (the region bounded by $C_k$). The winding number or index of $\Gamma$ around $a_k$ is the total number of counterclockwise turns that the object makes around $a_k$, $m_k = \text{Ind}_{\Gamma}(a_k) = \frac{1}{2\pi i} \oint_{\Gamma} \frac{dz}{z-a_k}$.

$m_k = 1$ means $\Gamma$ loops once counter-clockwise around the $k$-th hole and $m_k = -1$ means $\Gamma$ loops once clockwise around the $k$-th hole. Similarly, $m_k = 2$ means $\Gamma$ loops twice counter-clockwise. $m_k = 0$ means $\Gamma$ does not enclose the $k$-th hole at all.

Proof

This theorem is a direct consequence of the Deformation Principle. This means we can freely “deform” the contour $\Gamma$ anywhere within R without changing the value of the integral $\oint_{\Gamma} f(z)dz$. We can stretch it, shrink it, and move it, as long as we don’t cross any of the “holes” (the regions $Int(C_k)$) or the outer boundary $C$.

Besides, as we have previously demonstrated, any general contour $\Gamma$ in $R$ can be continuously deformed within $R$ into a new path that is just a combination of the inner boundary contours $C_k$.

How does the deformation work?

If $\Gamma$ loops $m_1$ times around the $C_1$ hole, $m_2$ times around $C_2$, and so on, we can deform $\Gamma$ (using the “cut” logic from the previous proof) so that it becomes a path that literally traces:

$C_1$, $m_1$ times. $C_2$, $m_2$ times. … $C_n$, $m_n$ times. The integrals over the “bridges” or “cuts” used to do this deformation all cancel out, just as they did in the previous proof. Since the integral is unchanged by this deformation, the integral over the original Γ must be equal to the integral over this new, “simplified” path:

$\oint_{\Gamma} f(z)dz = \int_{m_1 C_1 + m_2 C_2 + \cdots + m_n C_n} f(z)dz$

By the linearity of integrals, this is:

$\oint_{\Gamma} f(z)dz = m_1 \oint_{C_1} f(z)dz + m_2 \oint_{C_2} f(z)dz + \cdots + m_n \oint_{C_n} f(z)dz$

This is precisely the theorem:

$\oint_{\Gamma} f(z)dz = \sum_{k=1}^n m_k \oint_{C_k} f(z)dz$