Cauchy's Theorem for Simply Connected Domains

Tell me and I’ll forget; show me and I may remember; involve me and I’ll understand, Chinese Proverb

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

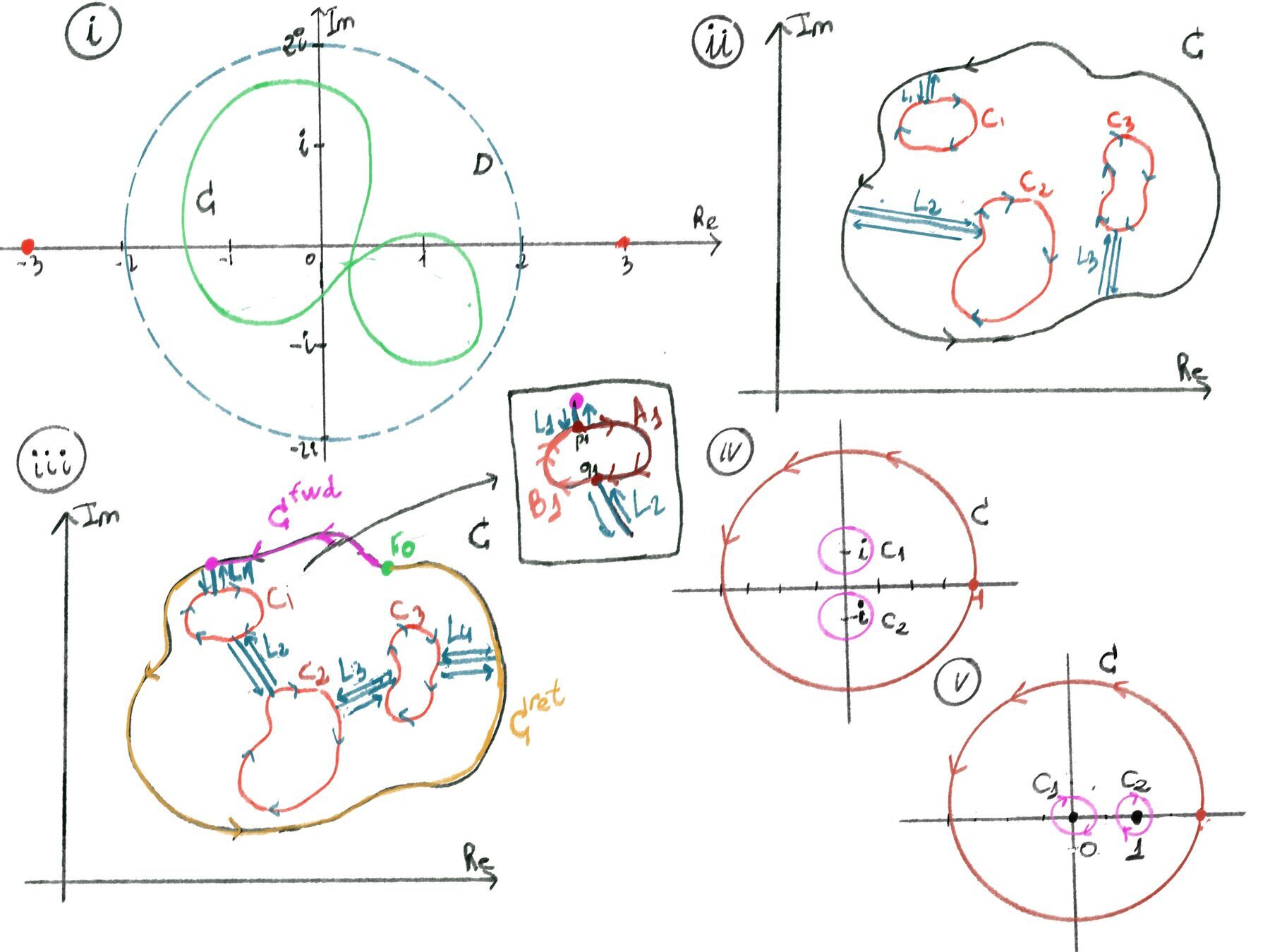
• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

Simply and multiply connected domains

Definition. A domain in complex analysis is a nonempty open (for every point $z_0$ in the set, there exists some radius r > 0 such that the open disk $D(z_0, r) = \{z : |z - z_0| < r\}$ is entirely contained in the set) connected (the set cannot be split into two disjoint nonempty open subsets) subset of $\mathbb{C}$.

Definition. A domain (an open, connected set) is simply connected if it has no holes (a “nice,” solid region). You can’t draw a closed loop inside it that circles around a point that is not in the domain. More formally, every simple closed curve (a loop that doesn't cross itself) within the domain can be continuously shrunk to a single point without ever leaving the domain.

Examples: the entire complex plane, $\mathbb{C}$; any disk (e.g., $\{z \in \mathbb{C} : |z| < 1\}$); a half-plane (e.g., the right half-plane $\{z \in \mathbb{C} : \text{Re}(z) > 0\}$); the interior of any simple closed curve (like a square or a circle).

Definition. A domain is multiply connected if it is not simply connected, i.e., it has at least one “hole.”. More formally, there exists at least one simple closed curve in the domain that cannot be continuously shrunk to a single point while staying within the domain. The curve will get stuck around a hole.

Examples: An annulus (a ring, the region between two circles), like $\{z \in \mathbb{C} : 1 < |z| < 3\}$ (any loop that winds around 0, e.g., the circle |z| = 2, cannot be shrunk to a point while staying within the domain); a punctured disk, like $\{z \in \mathbb{C} : 0 < |z| < 1\}$ (a disk with the center point removed). This has one hole (a “puncture”); the complex plane with several points removed, e.g., $\mathbb{C} \setminus \{0, 1\}$

Cauchy’s Theorem for simply connected domains

Cauchy’s Theorem for simply connected domains. If a function f is analytic (a function that is complex-differentiable at every point within a domain, i.e., well-behaved and smooth, with no sharp corners, breaks, or singularities like division by zero) throughout a simply simple connected domain D then $\oint_C f(z)dz = 0$ for every closed contour C lying in D.

A simply simple connected domain D has no holes, every simple closed contour C lying entirely in D can be shrunk to a point without any part of it ever leaving the domain, e.g., the entire complex plane $\mathbb{C}$, the interior of a circle, and the upper half-plane. Counterexamples: an annulus (a disk with a smaller disk removed from its center), or the complex plane with the origin removed $D = \mathbb{C} \setminus \{0\}$.

Proof.

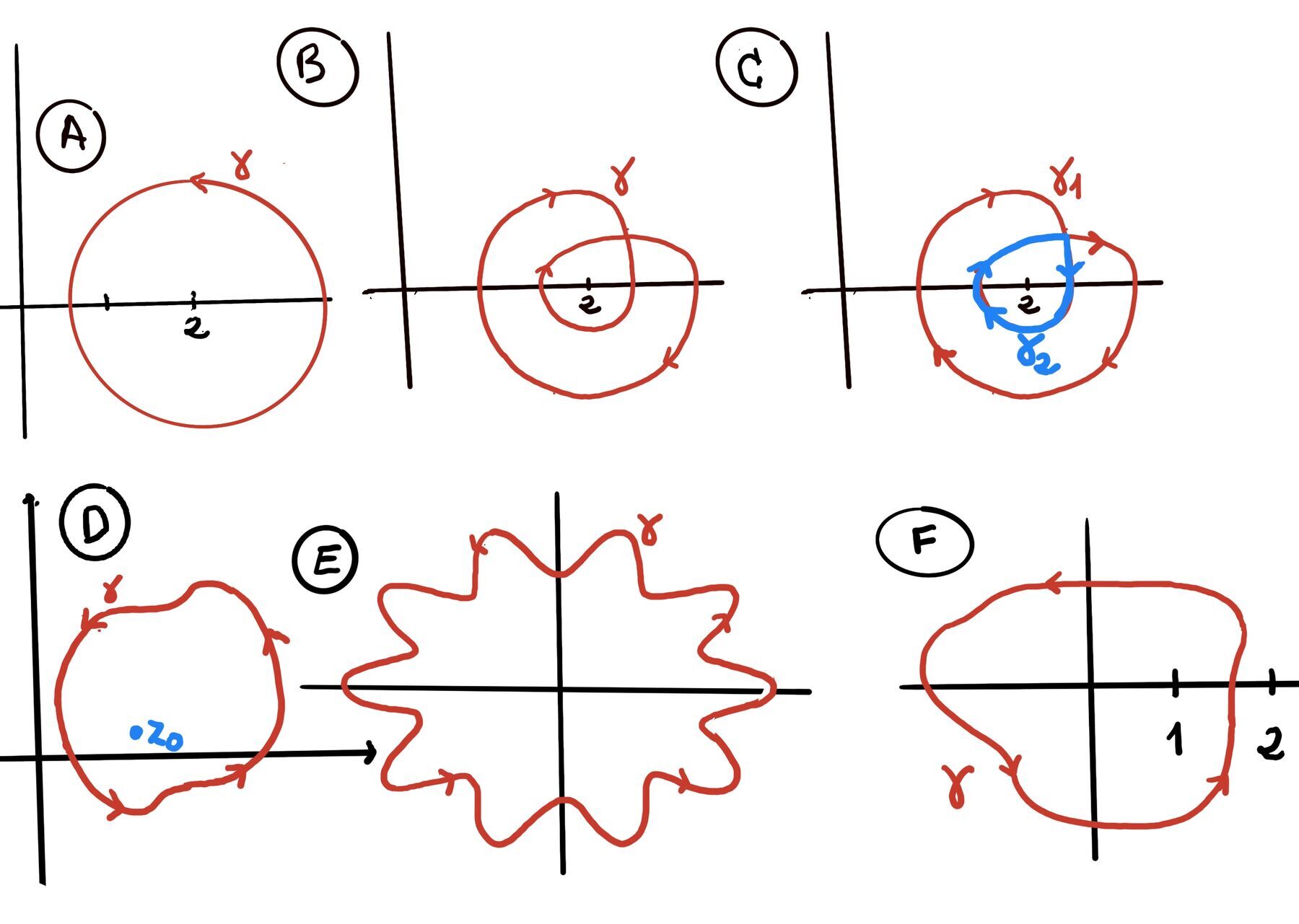
Case 1. If C is a simple close contour (a path that starts and ends at the same point but never crosses itself, e.g, a circle, an ellipse, or a distorted rectangle) lying entirely within the simply connected domain D.

Because D is simply connected (it has no holes), and the curve C lies completely within D, the entire region bounded by C (its interior) must also lie completely within D. There is no “hole” in D that the interior of C could possibly contain.

Recall, the Cauchy-Goursat theorem. If a function f is analytic at all points interior to and on a simple closed contour, then the integral of f around that contour is zero.

1. $f$ is analytic throughout the entire domain $D$.
2. The interior of $C$ and the boundary $C$ itself are both contained in $D$.
3. Therefore, $f$ is analytic at all points interior to and on $C$.

Since all conditions of the Cauchy-Goursat theorem are met, we can directly apply its conclusion: $\oint_C f(z)dz = 0$

Case 2. If C is closed but self-intersecting contour, meaning a path that starts and ends at the same point but crosses itself a finite number of times, e.g., a figure-eight.

The core idea is to show that the integral over the complex path is just the sum of the integrals over a set of simple closed paths. We can then apply the result from Case 1 to each simple path.

Let’s consider a figure-eight contour, which intersects itself once at a point $A$. This contour can be viewed as two separate simple closed loops, let’s call them $C_1$ (the left loop) and $C_2$ (the right loop). The original contour $C$ traverses these loops. For example, it might traverse $C_1$ counter-clockwise and then $C_2$ counter-clockwise.

Let the path segment that is shared during the intersection be denoted by the line from $A$ to $B$ (in reality, the intersection might just be a single point). When we calculate the integral over the full contour $C$, we travel along this shared segment in one direction for the first loop and in the opposite direction for the second loop, so the integrals over the shared path cancel out (a fundamental property of contour integrals is that reversing the direction of integration negates the value) and the integral over the entire self-intersecting contour $C$ is the sum of integrals over the simple loops $C_1$ and $C_2: \oint_C f(z)dz = \oint_{C_1} f(z)dz + \oint_{C_2} f(z)dz =[\text{ Case 1 }] 0 + 0 = 0.$

This logic can be extended to a contour $C$ with any finite number of intersections. It can always be decomposed into a finite number of simple closed contours ($C_1, C_2, \ldots, C_n$), and the integral over $C$ will be the sum of the integrals over each $C_k$. Since every individual integral is zero, according to the Cauchy-Goursat theorem, the total sum is zero: $\oint_C f(z)dz = \sum_{k=1}^n \oint_{C_k} f(z)dz = 0$

Examples

• Let C be any closed contour lying (e.g., the circle $|z|=1.5$ or a square centered at the origin with side length 2 or a closed contour like Figure i) that lies entirely within the open disk $D$ defined by |z| < 2. Then, $\oint_C \frac{zsin(z)}{(z²-9)^3}dz = 0$.

1. The domain $D$ is the open disk $|z| < 2$. This is a simply connected domain because it’s a solid disk with no holes in it. Any loop drawn inside it can be shrunk to a point without leaving the disk.
2. We look for points where $f(z)$ is not analytic (i.e., where it “blows up” or is undefined). This happens when the denominator is zero, z = ±3.
3. The contour $C$ lies entirely inside this domain. Both singularities $z=3$ and $z=-3$ are outside this domain.
4. Because the function $f(z)$ is analytic everywhere inside and on the contour $C$ (its only “problems”, more formally singularities, are far away), the Cauchy-Goursat theorem applies, and the integral must be zero.

• Let C be a semi-circle of radius $R=0.5$ in the upper half-plane, centered at $z=2i$, and closed by the straight line segment from $2i - 0.5$ to $2i + 0.5$ that lies entirely within the simply connected open domain Im(z) > 1. Then, $\oint_C \frac{e^z}{z^2+1} dz = 0$.

1. The domain D is the upper half-plane Im(z) > 1, the part of the plane “above” the line $y=1$. It is a simply connected open set.
2. We look for points where f(z) is not analytic (i.e., where it “blows up” or is undefined), z = ±i.
3. The contour C is centered at $2i$ (or $y=2$) and stays well within the region $y > 1$. The singularity $z = +i$ (or $y=1$) is on the boundary of this domain, but not inside it. The singularity $z = -i$ (or $y=-1$) is far outside the domain.
4. Because the function $f(z)$ is analytic everywhere inside and on the contour $C$ (its only “problems”, more formally singularities, are far away), the Cauchy-Goursat theorem applies, and the integral must be zero.

• Let C be any simple closed contour $C$ in the entire complex plane (e.g., a circle, a square, a triangle, or any complicated loop) that lies entirely in the complex plane. Then, $\oint_C (z^4 + 8z^3 -7z^2 + 3z + 4cos(z) -8sin(z))dz = 0.$

1. The domain $D$ is the entire complex plane $\mathbb{C}$. The entire plane is a simply connected (it has no “edges” and no “holes”) set.
2. We look for points where f(z) is not analytic (i.e., where it “blows up” or is undefined). However, this function is a combination of polynomials, the cosine and sine functions. They are all analytic everywhere (entire).
3. Since $f(z)$ is analytic everywhere, it is automatically analytic inside and on any closed contour $C$ you can possibly draw or imagine. Therefore, the integral is always zero.