Cauchy's Theorem for Rectifiable Jordan Curves

I’d far rather be happy than right any day, Douglas Adams, The Hitchhiker’s Guide to the Galaxy.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

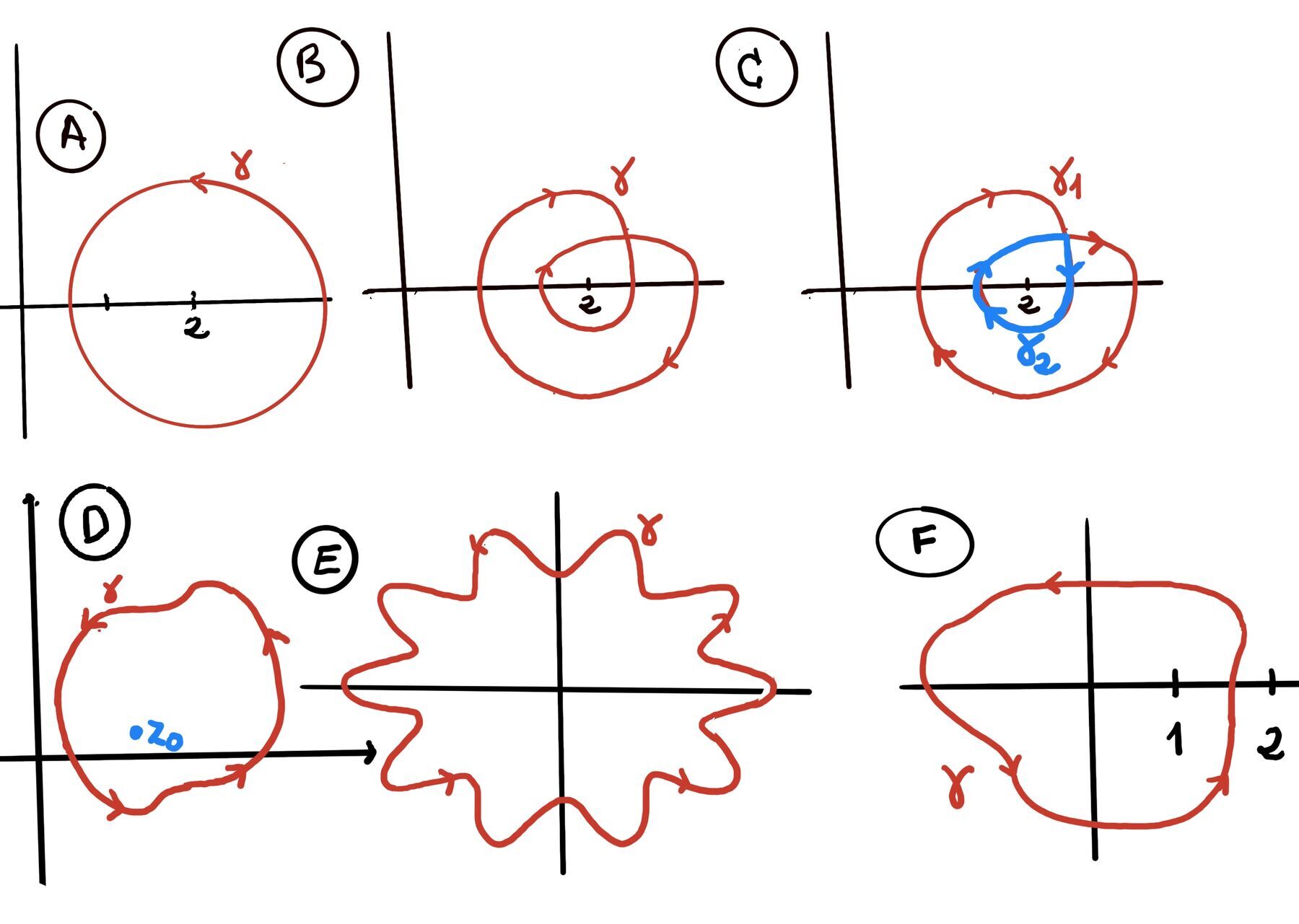
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Examples:

1. Circle. Let $\gamma(t)=Re^{it}, 0\le t\le 2\pi$. Then $\gamma$ is a positively oriented Jordan curve. For any $z_0$ with $|z_0| < R, Ind(\gamma; z_0)= 1, Ind(\gamma; z_0)=0 \text{ if } |z_0| > R$. Hence, $Int(\gamma)={|z| < R}$ and $Ext(\gamma)={|z| >R }$.
2. Simple polygon. Let $\gamma$ be the boundary of a simple polygon P traversed counterclockwise. Then, $Int(\gamma)=P^\circ$ (its interior as a planar region). For any $z_0\in P^\circ, Ind(\gamma; z_0) = 1; \text{ for } z_0\notin \overline{P}$, it is 0.
3. Orientation flip. If $\tilde\gamma$ is the same curve as $\gamma$ but clockwise, then $Ind(\tilde\gamma; z_0) = -Ind(\gamma; z_0)$. The sets $Int(\gamma)$ and $Int(\tilde\gamma)$ coincide, but their indices differ by sign.
4. Multiple windings. If $\gamma$ wraps around once, then $Ind(\gamma; z_0)=\pm1$ inside; if you traverse the same Jordan curve m times, the index inside is $\pm m$.

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

Rectifiable Jordan curves

Definition. A rectifiable Jordan curve is a curve γ in the complex plane satisfying four key properties:

• γ is Simple: The curve does not intersect itself. Formally, if γ: [a, b] → ℂ is a parameterization, then γ is injective on [a, b) (no self-intersections) and γ(a) = γ(b) (closed loop).
• γ is Closed: The curve has a finite length and returns to its starting point. In other words, it forms a complete loop, starting and ending at the same point.
• γ is rectifiable if its arc length is finite. This means that, regardless of the curve’s shape (smooth, piecewise smooth, or otherwise “tame”), the process of measuring its length as the “sum” of infinitesimal increments yields a finite value. The arc length of a curve is defined as the supremum of the lengths of all possible inscribed polygonal paths. For any finite ordered partition π, $a = t_0 < t_1 < \cdots < t_n = b$ of [a, b], the polygonal path joining the points $\gamma(t_0), \gamma(t_1), \ldots, \gamma(t_n)$ has length $L_π(\gamma) = \sum_{i=1}^{n} d(\gamma(t_{i-1}), \gamma(t_i)).$ The length of $\gamma$ is defined as $L(\gamma) = \sup_{π∈Π} L_π(\gamma) = \sup_{π∈Π} \{ \sum_{i = 1}^n d(\gamma(t_{i-1}), \gamma(t_i)) : a=t_0 < t_1 < \cdots < t_n =b \}$ where the supremum runs over all finite partitions of [a, b].

Rectifiability is automatic if γ is piecewise C¹ (each smooth piece has a continuous derivative) or C¹ (the function or curve is continuously differentiable: it has a derivative everywhere, and that derivative is continuous; the curve is smooth (no jumps or cusps) and its tangent vector $\gamma'(t)$ varies continuously with t) with γ′ ∈ L¹ (it is integrable in the Lebesgue sense: the integral of its absolute value is finite). Corners are allowed; self-intersections are not.

How to check rectifiability quickly. If $\gamma:[a,b] \to \mathbb{C}$ is piecewise $C^1$ and $\int_a^b |\gamma'(t)|dt < \infty$, then $\gamma$ is rectifiable. If $\gamma$ is a simple polygon or a $C^1$-perturbation of a circle, it’s rectifiable.

• Jordan Curve Property: By the Jordan curve theorem, Γ divides the plane into two disjoint regions: A bounded interior (Int(Γ)) and an unbounded exterior.

Examples: polygons, i.e., simple closed shapes with straight sides (triangles, rectangles, pentagons, etc., length = sum of side lengths -finite-, e.g., a unit square with vertices at 0, 1, 1+i, i.), circles and ellipses (e.g., the unit circle $γ(t) = e^{it}, t ∈ [0, 2π]$), piecewise smooth curves (curves composed of finitely many smooth (C¹) arcs. Length = sum of arc lengths of smooth segments, e.g., semicircle $γ₁(t) = e^{it}, t ∈ [0, π]$, line segment γ₂(t) = -1 + 2t, t ∈ [0, 1]), and curves defined by y = f(x) where f is continuous and of bounded variation (the total variation over the interval is finite, it doesn’t oscillate wildly, e.g, a closed curve formed by the graph of f(x) = sin(x) on [0, π]). Non-Examples: Koch snowflake (Infinite length, it is a fractal curve), figure-eight curve (self-intersect at the origen, i.e., not simple), open line segment (not closed), and pace-filling curves such as the Peano Curve (infinite length and self-intersecting).

Cauchy’s Theorem for Rectifiable Jordan Curves

Cauchy’s Theorem for rectifiable Jordan curves. Let Γ be a rectifiable Jordan curve (simple, closed, finite length), positively oriented, and let f be analytic on an open set Ω containing Γ* ∪ Int(Γ). Then, $\oint_{\Gamma} f(z)dz = 0.$

Proof:

1. Tubular Neighborhood Construction: Since Γ ∪ Int(Γ) is compact (closed -contains all its limit points- and bounded) and Ω is open, there exists ε > 0 such that the tubular neighborhood $U_\varepsilon = \{ z \in \mathbb{C} : \text{dist}(z, \Gamma \cup \text{Int}(\Gamma)) < \varepsilon \} ⊂ \Omega$ on which f is analytic.

   This set $U_\varepsilon$ is an open “thickening” of Γ ∪ Int(Γ) — imagine drawing a curve and then shading a small band around it. Since $\Omega$ is open, then every point on $\Gamma$ and in $\text{Int}(\Gamma)$ has a little open ball around it that stays inside $\Omega$. So we can take the union of all these balls — and that union is precisely the tubular neighborhood $U_\varepsilon$. Note: The distance function is $\text{dist}(z, A) := \inf_{w \in A} |z - w|$.

2. Polygonal approximation lemma. For any δ > 0 there exists a simple polygon $P_δ ⊂ U_ε$ such that: $P_δ$ is positively oriented, uniformly δ-close to Γ (the Hausdorff distance between Γ and $P_δ$ is less than δ, $d_H(Γ, P_δ) < δ$), and Γ and $U_δ$ are homotopic in $U_ε$ (the region between them is contained in $U_ε$ and free of singularities).

   For two sets A and B, the Hausdorff distance is: $d_H(A, B) = max \{ sup_{a \in A}d(a, B), sup_{b \in B}d(A, b) \}$, where $d(a, B):= \{ inf_{b \in B} d(a, b) \}$ and sup represents the supremum operator, inf the infimum operator. The infimum of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S. Intuitively: It’s the smallest ε such that every point of A is within ε of some point of B, and vice-versa.

   Construction sketch: Choose finitely many points on Γ, connect consecutive points by line segments short enough that the resulting chordal polygon stays inside $U_ε$ (by triangle inequality, any point on the line segment between two close points on Γ remains close to Γ). For sufficiently small δ, this polygon is simple (since Γ is simple, sufficiently fine sampling prevents the polygon from self-intersecting) and approximates Γ uniformly (short line segments between nearby points on Γ cannot deviate far from Γ).

3. Application of Cauchy’s Theorem for Polygons: Since f is analytic on $U_ε ⊃ P_δ ∪ Int(P_δ)$ and $P_δ$ is a polygon, Cauchy’s theorem for polygons gives: $\oint_{P_δ} f(z) dz = 0.$
4. Deformation principle. The curves Γ and $P_ε$ are two homotopic in $U_ε$ and f is analytic on $U_ε$. Therefore, by the homotopy invariance of contour integrals: $\oint_\Gamma f(z) dz = \oint_{P_δ} f(z) dz = 0.$
5. Conclusion. Every rectifiable Jordan curve enclosing a region where f is analytic acquires the zero integral by uniform polygonal approximation plus deformation. Hence, Cauchy’s theorem holds for all such curves, not just polygons.

Examples

• A “wobbly circle” (smooth, simple, finite length). Let $\gamma(t) = \bigl(1+\varepsilon \cos (5t)\bigr)e^{it}, 0\le t\le 2\pi,$ with $0 < \varepsilon < 1$. Then $\gamma$ is a simple closed ($C^1$) curve (no self–intersections for small $\varepsilon$); $\gamma'$ is continuous, hence its length is finite $\int_0^{2\pi}|\gamma'(t)| dt < \infty$. Thus, $\gamma$ is a rectifiable Jordan curve, fully satisfying the conditions for the Cauchy-Goursat theorem.

What this curve looks like? This is a polar equation where the angle is t (from $e^{it}$) and the radius is $r(t) = 1+\varepsilon \cos (5t)$. As t goes from 0 to $2\pi$ (one full rotation), the $\cos(5t)$ term oscillates 5 times. This makes the radius “wobble” in and out 5 times, creating a shape like a 5-petal flower.

Take $f(z) = e^z$ (entire, meaning it is analytic on the entire complex plan). Since (f) is analytic on $\mathbb{C}, \text{ by the Cauchy-Goursat theorem, the integral must be zero } \oint_{\gamma} e^z dz = 0.$

Why this is interesting. The boundary has lots of curvature and no straight segments, but Cauchy’s theorem cares only about analyticity inside the loop—not about the shape.

• A simple polygon (corners allowed). Consider the square contour $\gamma$ defined by the vertices $0\to 2 \to 2+2i \to 0+2i \to 0$ traversed counterclockwise. This is a rectifiable Jordan curve with arc length 8 (each side has length 2). Take the polynomial function $f(z) = z^7-3z+1$, which is entire (analytic everywhere in ℂ). By Cauchy’s theorem for polygons, since γ is a closed polygonal contour lying entirely within the simply connected domain ℂ, and f is analytic in ℂ, we have: $\oint_{\gamma} f(z)dz = 0.$

We can verify this directly by noting that f(z) has an antiderivative $F(z) = \frac{z^8}{8} - \frac{3z^2}{2} + z$. By the fundamental theorem of calculus for contour integrals: $\oint_γ f(z)dz = F(0)−F(0)=0$,since the contour starts and ends at the same point (0). This confirms the result.

Corners do not affect the conclusion; analyticity on and inside the square is all that matters. The existence of an antiderivative for entire functions provides an alternative verification method.

• Curve with a cusp but finite length (piecewise $C^1$). Let’s define the upper arc $\sigma(t) = t+i|t|$ from (-1 -i) up to (1 +i), this is a curve from (-1, -1) to (1, 1). Close the loop by adding three line segments ((1, 1) to (1, 2); (1, 2) to (-1, 2); (-1, 2) to (-1, -1)) to form a simple closed curve.

This is a trapezoid with a “pointy” bottom at (0, 0); at (0,0), the curve has a sharp corner where the two diagonal segments meet. This closed curve is rectifiable (finite total length), simple, but not $C^1$ at the cusp.

It is piecewise C¹ (smooth everywhere except at (0,0) where it’s not differentiable). For any entire (f) (e.g., f(z) = sin(z), z², etc.), $\oint_{\gamma} f(z)dz = 0.$

Takeaway: Differentiability of the path is not required for Cauchy’s theorem; only finite length (rectifiability) and no self-intersection (simple closed curve) are needed, along with analyticity of f on and inside the contour.

• Star-shaped $C^1$ boundary (analytic everywhere) Let γ be the smooth, simple, star-shaped loop $\gamma(t) = \bigl(2+\tfrac12\sin(3t)\bigr)e^{it}, 0\le t\le 2\pi$.

The general polar equation for a rose curve is 𝑟 = 𝑎sin(𝑛𝜃) or 𝑟 = 𝑎cos(𝑛𝜃), but a modified version with a constant added, like 𝑟 = 𝑎 + 𝑏sin(𝑛𝜃), is sometimes called a “star-shaped” curve, especially when it is not centered at the origin.

What this curve looks like? This is a polar equation where the angle is t (from $e^{it}$) and the radius is $r(t) = 2+\tfrac12\sin(3t)$. As t goes from 0 to $2\pi$ (one full rotation), the value of sin(3t) oscillates between -1 and 1, and $2+\tfrac12\sin(3t)$ varies between $2+\tfrac12(-1) = 1.5$ and $2+\tfrac12(1) = 2.5$, so γ encloses the origin but never passes through it and is obviously C¹ with |γ′(t)| bounded; hence γ has finite length.

The sin(3t) term causes the radius to vary periodically as the curve rotates. Since the period of sin(3t) is $\frac{2\pi}{3}$, the radius will oscillate three times as t goes from 0 to 2𝜋. This creates a three-petaled rose curve. The curve would resemble a smooth, three-leaf clover shape with its center lobes at a distance of 2.5 from the origin and the inward-curving parts at a distance of 1.5 from the origin.

If f is any entire function f(z) = cos(z), z² + 8, e³ + sin(z) + 3z, etc., then f is analytic on and inside γ. By Cauchy–Goursat, $\oint_{\gamma} f(z)dz = 0$.

Thus the “wiggly star” behaves exactly like a circle: no singularity inside ⇒ zero integral.

• Counterexample: singularity outside. Let $\gamma$ be the circle |z -3| = 1, center 3 and radius 1. Take $f(z)=\dfrac{1}{z}$, which is analytic on and inside $\gamma$ because the singularity at 0 is outside the loop. Then, $\oint_{\gamma}\frac{dz}{z}=0.$ If we instead take $\gamma$ as the unit circle |z| = 1, then 0 lies inside the curve, and $\oint_{\gamma}\frac{dz}{z}=2\pi i\neq 0$. Cauchy’s theorem does not apply there because f is not analytic on $Int(\gamma)$.

• Piecewise circular + linear boundary (lens). Let $\gamma$ be a simple closed curve formed by the upper semicircle of |z - 1| = 1 from 0 to 2, the horizontal segment [0, 2] on the real axis, and the lower semicircle part of |z - 1| = 1 from z = 2 back to z = 0. This encloses a lens-shaped region. This $\gamma$ is rectifiable and simple.

For any entire function f, e.g., $f(z) = z^3; z^2 + 3z + 5; z^n, n \in \mathbb{N}; \sum_{k=0}^m a_k z^k, a_k \in \mathbb{C}; e^{az+b}, a, b \in \mathbb{C}; \cos z; \cos(z^3 + 2z); e^{\sin z}$, $\oint_{\gamma} f(z) dz=0.$

You can also approximate $\gamma$ uniformly by inscribed polygons and pass to the limit; the integrals are zero along each polygon by the polygonal version of Cauchy’s theorem.

• Using the Fundamental Theorem of Calculus for contours. If f has an antiderivative F, i.e., f = F’ that is analytic on a neighborhood containing the contour γ and its interior $\gamma^*\cup Int(\gamma)$, then for any rectifiable Jordan curve γ: $\oint_{\gamma} f(z)dz=\oint_{\gamma} F'(z)dz = F(\gamma(b))-F(\gamma(a)) = 0$. This holds because γ is closed (γ(a) = γ(b)), so the net change in F around the contour is zero.

Consider the function $f(z) = 3z^2 +2z$ so F(z) = $z^3+z^2$. For any rectifiable Jordan curve (whether smooth, piecewise smooth, or with corners), we have: $\gamma$ in $\mathbb{C}$, $\oint_{\gamma} (3z^2+2z)dz=0.$

This result is more general than Cauchy’s theorem for rectangles or polygons - it applies to any rectifiable Jordan curve as long as f has an antiderivative analytic on a neighborhood containing the contour and its interior. The existence of an antiderivative is a stronger condition than mere analyticity, but when it holds, the integral over any closed contour vanishes.