Continuous Argument Function for Complex Numbers: A Comprehensive Guide

When you have eliminated the impossible, whatever remains, however improbable, must be the truth, Sherlock Holmes.

Continuous Argument Function for Complex Numbers: A Comprehensive Guide

Introduction to the Argument of a Complex Number

A complex number z can be expressed in the form: z = x + yi where x and y are real numbers, and i is the imaginary unit with the property that $i^2 = -1$.

The argument of a complex number is a fundamental concept in complex analysis. For a non-zero complex number $z = x + iy \neq 0$, its argument (denoted $\arg(z)$) is the angle $\theta$ between the positive real axis and the vector connecting the origin to z in the complex plane. This angle is typically measured in radians, with the principal value (the most commonly used) ranging between $-\pi$ and $\pi$, or sometimes 0 and $2\pi$.

For any nonzero complex number z = x + iy, the argument is the angle $\theta$ such that: $z = |z| e^{i\theta}, \theta = \arg(z) = \tan^{-1}\left(\frac{y}{x}\right), |z| = \sqrt{x^2+y^2}$

If $z = x + iy \neq 0: \arg(z) = \theta \text{ satisfying } x = |z|\cos\theta, y = |z|\sin\theta.$ The principal value $\mathrm{Arg}(z)$ is a single‑valued choice of $\arg(z)$ — usually in $(-\pi,\pi]$ — but because angles are defined up to multiples of 2π, the full argument is multi‑valued: $\arg(z) = \{\mathrm{Arg}(z) + 2\pi k, k\in\mathbb{Z}\}$.

Properties of the Argument Function

Let z = x + iy ≠ 0.

1. Periodicity: The argument function is periodic with a period of $2\pi$. This means that for any integer k, $\arg(z) = \mathrm{Arg}(z) + 2\pi k$.
2. Principal Range: The principal value of the argument, usually denoted as $\text{Arg}(z)$, is typically taken in the interval $(-\pi, \pi]$ (by convention, other intervals of length 2π are possible).
3. Uniqueness: While a complex number has infinitely many arguments differing by integer multiples of $2\pi$, the principal value provides a unique representation within its defined range.

However, the standard argument function has a critical limitation: it is not continuous everywhere in the complex plane. When moving around the origin (e.g., traversing a circle), the argument “jumps” by $ 2\pi $ at the point where the angle crosses a boundary (e.g., from $ \pi $ to $ -\pi $ or vice versa). This discontinuity arises because the argument is inherently multi-valued, and the standard definition restricts it to a specific interval.

Consider a complex number $ z = e^{i\theta} $ (a point on the unit circle) as $ \theta $ increases from $ 0 $ to $ 2\pi $. If we use Arg(z) ∈ (−π, π]:

• Approaching a point on the negative real axis from the upper half-plane $\theta \in [0, \pi)$ yields $ \operatorname{Arg}(z) = \theta, \operatorname{Arg}(z) \approx \pi$
• Approaching a point on the negative real axis from the lower half-plane $\operatorname{Arg}(z)$ suddenly drops to $-\pi$.
• This jump breaks continuity, even though the path $z(\theta)$ is smooth. It exhibits a jump of $2\pi$ when crossing a specific ray from the origin, such as the negative real axis for the $(-\pi, \pi]$ branch.

Therefore, we define the argument as a multi-valued function: $\arg(z) = \\{\theta_0 + 2\pi n : n \in \mathbb{Z}\\}$.

Why no continuous global definition? The domain $\mathbb{C} \setminus \{0\}$ is not simply connected — it has a “hole” at the origin. This topological property causes trouble when trying to define arg(z) continuously on the entire domain:

• If you traverse a closed path around the origin (e.g., the unit circle), the angle $\theta$ increases by $2\pi$.
• Therefore, any attempt to define $\arg(z)$ continuously on all of $\mathbb{C} \setminus \{0\}$ will fail to return to the same value after a full loop — a contradiction to continuity.

This is a classic example of a monodromy phenomenon: the value of a function changes when you loop around a singularity.

What about branches? To obtain a single-valued, continuous version of arg(z), you must restrict the domain by introducing a branch cut. For example:

• Remove the negative real axis: define arg(z) on $\mathbb{C} \setminus (-\infty, 0]$, where it’s continuous and takes values in $(-\pi, \pi)$.
• This is called the principal branch of the argument.

More generally, you can remove any ray from the origin to define a continuous branch:

• Removing the non-negative real axis [0, ∞) allows defining a continuous argument function taking values in (0, 2π).
• Removing a ray at angle $\alpha$ (i.e., {$re^{i\alpha} :r≥0$}) allows defining a continuous argument function taking values in ($\alpha, \alpha + 2\pi$).

Let z ≠ 0, arg(z) = {θ₀ + 2nπ: n ∈ ℤ} where $θ₀ = tan^{-1}(\frac{Im(z)}{Re(z)})$.

• If Re(z) = x = 0 and Im(z) = y > 0, then $\arg(z) = θ₀ = \frac{\pi}{2}$
• If Re(z) = x = 0 and y < 0, then $\arg(z) = θ₀ = -\frac{\pi}{2}$

Proposition. There is no continuous function θ : $\mathbb{C} \setminus \{0\} → \mathbb{R}$ such that θ(z) ∈ arg(z) for all $z \in \mathbb{C} \setminus \{0\}$.

Proof.

Assume, for the sake of contradiction, that such a continuous function θ exists. Define a function g: ℝ→ℝ by: g(t) = $\frac{1}{2\pi}(θ(e^{it})+θ(e^{-it})), t \in \mathbb{R}$

Since by assumption θ is continuous and the exponential function is continuous, g is continuous. For each t, note that: $θ(e^{it}) = t + 2n_t\pi, θ(e^{-it}) = -t + 2m_t\pi$ for some integers nₜ and mₜ.

Therefore, $g(t) = \frac{1}{2\pi}(θ(e^{it})+θ(e^{-it})) = \frac{1}{2\pi}(t + 2n_t\pi -t + 2m_t\pi) = \frac{1}{2\pi}(2(n_t\pi + m_t\pi)) = n_t + m_t \in \mathbb{Z}$.

Thus, g is a continuous integer-valued function on ℝ. The only continuous functions from ℝ to ℤ are constant functions, so g must be constant.

The only continuous functions from ℝ to ℤ are constant functions: 1. $\mathbb{Z}$ is discrete in the standard topology — each singleton {n} is open and closed (its complement is a union of other singletons, which are all open). 2. If $f:\mathbb{R} \to \mathbb{Z}$ is continuous, the preimage $f^{-1}(\\{n\\})$ is open and closed in ℝ for every integer n (continuity preserve openness and closeness). 3. The real line is connected, so the only subsets of $\mathbb{R}$ that are both open and closed (“clopen”) are $\varnothing$ and $\mathbb{R}$ itself. 4. $f^{-1}(\\{n\\})$ must be either empty or all of $\mathbb{R}$. That means f is constant.

Now evaluate g at specific points. At t = 0, g(0) = $\frac{1}{2\pi}(θ(e^{i0})+θ(e^{-i0})) = \frac{1}{2\pi}(θ(1)+θ(1)) = \frac{1}{\pi}(θ(1))$

Since θ(1) ∈ arg(1) = {2πn : n ∈ ℤ}, we have θ(1)= 2πk for some integer k. Thus: $g(0) = \frac{1}{\pi}(2\pi k) = 2k$, an even integer.

At t = π: $g(\pi) = \frac{1}{2\pi}(θ(e^{i\pi})+θ(e^{-i\pi})) = \frac{1}{2\pi}(θ(-1)+θ(-1)) = \frac{1}{2\pi}(2(θ(-1))) = \frac{1}{\pi}(θ(-1))$

Since θ(−1) ∈ arg(−1) = {(2n+1)π : n ∈ ℤ}, we have θ(−1) = (2k′ + 1)π for some integer k′. Thus: $g(\pi) = \frac{1}{\pi}((2k^′ + 1)\pi) = 2k^′′ + 1 \in \mathbb{Z}$, an odd integer ⊥ Since g is constant, we must have g(0)=g(π), but this implies an even integer equals an odd integer, which is a contradiction. Therefore, no such continuous function θ exists.

Conclusion: The argument function theta in the complex plane is classified as a multifunction due to its infinite values for each input.

Constructing Continuous Argument Functions via Branch Cuts

When we remove a ray from the origin (a branch cut), we can define continuous single-valued branches of the argument function. This works because removing a ray makes the domain simply connected, eliminating the topological obstruction that causes multi-valuedness.

• Removing the Non-Negative Real Axis.

Consider the domain ℂ \ [0, ∞) (complex plane without the non-negative real axis). The multi-valued argument function maps each z to the set: $arg(z) = \\{\theta_0 + 2\pi n \mid n \in \mathbb{Z}\\}$ which can be visualized as the union of intervals: $\cdots \cup (-2\pi, 0) \cup (0, 2\pi) \cup (2\pi, 4\pi) \cup \cdots$

By selecting the interval (0, 2π), we can construct a continuous single-valued argument function: $\theta: \mathbb{C} \setminus [0, \infty) \to (0, 2\pi)$

This branch satisfies: (i). For z in the upper half-plane (y > 0): $\(0 < \theta(z) < \pi\)$, (ii). For z in the lower half-plane (y < 0): $\(\pi < \theta(z) < 2\pi\)$. (iii). As z approaches the positive real axis from above: $y \to 0^+, x \gt 0: \theta(z) \to 0^+$. (iv) As z approaches the positive real axis from below: $y \to 0^-, x \gt 0: \theta(z) \to 2\pi^-$

• Removing the Non-Negative Real Axis.

Now consider removing the ray at the angle π/4 (45°), defined as: $\text{Ray} = \\{re^{i\pi/4} \mid r \geq 0\\}$. The domain is ℂ \ Ray.

The multi-valued argument maps to the set: $\arg(z) = \\{\theta_0 + 2\pi n \mid n \in \mathbb{Z}\\}$ which corresponds to the union of intervals: $\cdots \cup (\pi/4 - 4\pi, \pi/4 - 2\pi) \cup (\pi/4 - 2\pi, \pi/4) \cup (\pi/4, \pi/4 + 2\pi) \cup \cdots$

By selecting the interval (π/4, π/4 + 2π), we construct a continuous single-valued argument function: $\theta: \mathbb{C} \setminus \text{Ray} \to (\pi/4, \pi/4 + 2\pi)$

This branch satisfies: (i) For points just above the ray (As we get closer to the ray from above, the argument values approach π/4 from above): $\theta(z) \to (\pi/4)^+$; (ii) For points just below the ray (As we get closer to the ray from below, the argument values approach π/4 + 2π from below): $\theta(z) \to (\pi/4 + 2\pi)^-$; (iii) As we traverse a circle around the origin (avoiding the ray), θ(z) increases continuously from π/4 to π/4 + 2π

Why This Works

1. Simply Connected Domain: Removing a ray makes the domain simply connected (no holes), allowing continuous single-valued branches.
2. Branch Cut Selection: The ray acts as a barrier preventing loops around the origin.
3. Interval Selection: We choose an interval of length 2π that doesn’t include the direction of the ray.
4. Continuity: The function is continuous because the argument function behaves smoothly and continuously, approaching the cut from either side gives values that approach the endpoints of the selected interval. From above, it approaches π/4 (but never reaches it); from below, it approaches π/4 + 2π (but never reaches it).

Computation

In practice, the argument is computed using the atan2(y, x) function, which accounts for the quadrant of $ z $ in the complex plane.

For $z = x + iy = |z|e^{i·\theta}$,

arg(z) is a multi-valued function given by $|z|=\sqrt{x^2+y^2}, \text{arg(z)} = \\{\theta + 2\pi·n: n \in \mathbb{Z}\\}$.

$\theta = \text{Arg(z)} = \text{atan2}(y, x)$ is a single-valued branch, which by convention is taken to lie in the range $-\pi < \theta ≤ \pi$

For $z = re^{i\theta}$ with r > 0, we define: $\theta(z) = \text{Arg(z)} = \begin{cases} \tan^{-1}\left(\frac{y}{x}\right), & \text{if } x > 0 \\\\ \tan^{-1}\left(\frac{y}{x}\right) + \pi, & \text{if } x < 0 \text{ and } y \geq 0 \\\\ \tan^{-1}\left(\frac{y}{x}\right) - \pi, & \text{if } x < 0 \text{ and } y < 0 \\\\ +\frac{\pi}{2}, & \text{if } x = 0 \text{ and } y > 0 \\\\ -\frac{\pi}{2}, & \text{if } x = 0 \text{ and } y < 0 \\\\ \text{undefined}, & \text{if } x = 0 \text{ and } y = 0 \end{cases}$

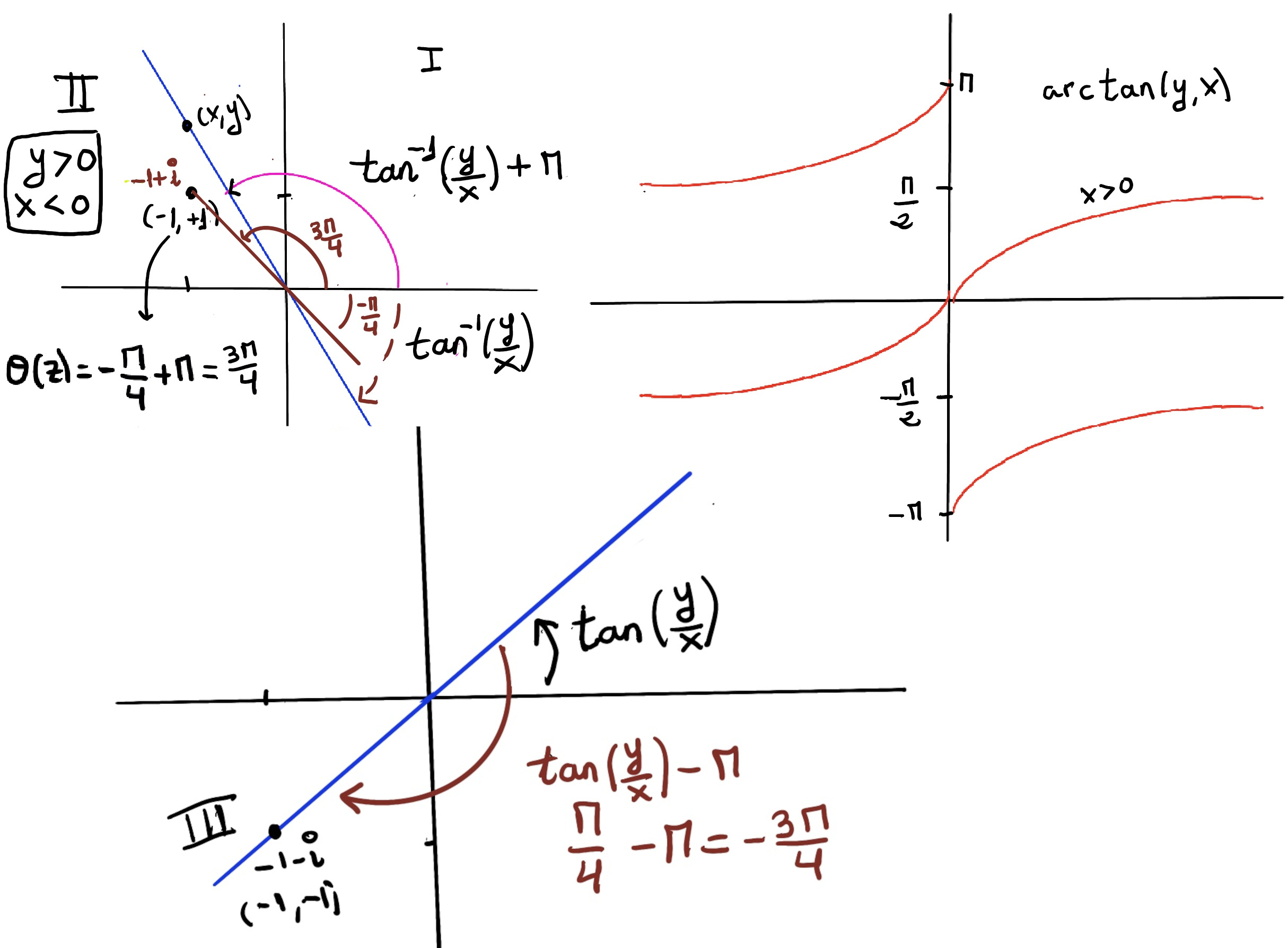
Quadrant Handling:

1. x > 0: Right half-plane (quadrants I and IV).
2. x < 0: Left half-plane (quadrants II and III), adjusted by ±π to stay within (−π,π].
3. x = 0: Pure imaginary axis (θ = ±π/2).

Why $tan^{-1}(\frac{y}{x})$ is insufficient: The standard $tan^{-1}$ only returns values in (−π/2, π/2). The atan2(y, x) function resolves quadrant ambiguities by using both x and y signs.

This implementation ensures continuity everywhere except along the negative real axis, where there’s a branch cut (jumping from π to -π). This formulation is exactly what’s implemented in most programming languages and mathematical software, making it the standard practical approach for complex number computations.

Examples

1. Example 1: z = 1 + i. Here, x = 1 > 0, the argument is $\theta(z) = \tan^{-1}(1/1) = \frac{\pi}{4}$.

2. Example 2: z = -1 + i. Here, x = -1 < 0 and y = 1 ≥ 0, $\theta(z) = \tan^{-1}(1/-1) + \pi = -\frac{\pi}{4} + \pi = \frac{3\pi}{4}$.

3. Example 3: z = -1 - i. Here, x = -1 < 0 and y = -1 < 0. $\theta(z) = \tan^{-1}(-1/-1) - \pi = \frac{\pi}{4} - \pi = -\frac{3\pi}{4}$.

Programming Languages

• Wolfram Language (Arg[z]): Returns the principal value $(-\pi, \pi]$.
• Maple (argument(z)): Similar to Wolfram, with the same interval.
• MATLAB (angle(z)): Also uses $ (-\pi, \pi] $, while atan2(y, x) is explicitly used for quadrants.
• Python: cmath.phase

# Import cmath Library
import cmath

# Print quadrant-aware arctangent
print (cmath.phase(1 + 1j))
# 0.7853981633974483

Algebraic Identities

• Multiplication: $ \arg(z_1 z_2) = \arg(z_1) + \arg(z_2) \mod 2\pi $.
• Powers: $ \arg(z^n) = n\arg(z) \mod 2\pi $ for integer $ n $.
• Conjugate: $ \arg(\overline{z}) = -\arg(z) \mod 2\pi $.
• De Moivre’s Theorem: $ z^n = r^n(\cos(n\theta) + i\sin(n\theta)) \text{ where } z = re^{i\theta}$.