Logarithm as a Multifunction in the Complex Plane

To raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advance in science, Albert Einstein.

Any fool can make things complicated, it requires a genius to make things simple, E.F. Schumacher

The Complex Exponential Function

The complex exponential function, denoted as eᶻ or exp(z), is one of the most important functions in all of mathematics. It is the unique entire function that extends the real exponential function eˣ to the complex plane. This function is not only entire but also periodic.

To define the complex exponential function, we seek a function f: ℂ→ℂ that satisfies two key properties:

1. f(z₁ + z₂) = f(z₁)·f(z₂) for all z₁, z₂ ∈ ℂ
2. Consistency with the Real Exponential: f(x) = eˣ where x is a real number.

Let z = x + iy, where x, y ∈ ℝ. f(z) = f(x + iy) =[1] f(x)·f(iy) =[2] eˣ·f(iy)

Writing f(iy) = A(y) + iB(y), f(z) = eˣ·A(y) + ieˣ·B(y), where A(y) and B(y) are real-valued functions of y.

For f(z) to be a well-behaved function, we want it to be differentiable everywhere, which means it must satisfy the Cauchy-Riemann equations. The real and imaginary parts of f(z) are: u(x, y) = eˣ·A(y), v(x, y) = eˣ·B(y). The partial derivatives are uₓ = eˣ·A(y), u_y = eˣ·A’(y), vₓ = eˣ·B(y), and v_y = eˣ·B’(y).

Applying the Cauchy-Riemann equations, uₓ = v_y and u_y = - vₓ, we get: eˣ·A(y) = eˣ·B’(y), then, A(y) = B’(y). Similarly, eˣ·A’(y) = - eˣ·B(y), then A’(y) = -B(y).

From these two equations, we can derive a second-order differential equation for B(y): B’’(y) = -B(y) ↭ B’’(y) + B(y) = 0. This linear, homogeneous, constant-coefficient ODE has characteristic equation r² + 1 = 0 ⇒ r = ±i, the general solution is $y(t) = e^{at}(αcos(bt) + βsin(bt))$, where ‘α’ and ‘β’ are real numbers.

From A(0) = 1 and B(0) = 0 ⇒ β = 1, α = 0. Thus, we have uniquely determined the functions A(y) and B(y): B(y) = sin(y), A(y) = cos(y). Substituting these back into the expression for f(z), we arrive at the definition of the complex exponential function, f(z) = eˣ·cos(y) + ieˣ·sin(y) = eˣ(cos(y) + isin(y)).

The exponential function is well-defined for all z ∈ ℂ, entire, consistent with the real exponential, non-zero, periodic with period 2πi ($e^{z+2\pi i}=e^z $), $\frac{d}{dz}e^z = e^z$, and can be represented as a power series $e^z = \sum_{n=0}^∞ \frac{z^n}{n!}$ (it has infinite radius of convergence).

Logarithm Multifunction: A Comprehensive Exploration

Introduction to Logarithms in Real Numbers

In real analysis, the logarithm is a fundamental function defined for positive real numbers. For a base $ b > 0 $ ($b \neq 1$), the logarithm $ \log_b(x) $ provides the answer to the question: “To what power or exponent must we raise or elevate the base b to obtain x?”. More formally, $\log_b(x) = y \text{ if and only if } b^y = x$, e.g., $\log_{10}(100) = 2$ because $10^2 = 100$, $\log_{2}(8) = 3$ because $2^3 = 8$, $\ln(e^3) = 3$ (natural logarithm with base $e$), etc.

Key Properties

• Positivity of the argument: $\log_b(x)$ is undefined for $x \le 0$ in the real numbers.
• Base restriction: b can’t be $1, and must be positive.
• Inverse relationship: The logarithm is the inverse of the exponential function $b^y$. Logarithms undo the work of exponents, making them essential for solving equations where variables are in the exponent.
• Monotonicity: If $b > 1$, $\log_b(x)$ increases with $x$. If $0 < b < 1$, $\log_b(x)$ decreases with $x$.
• It is a single-valued function in the real domain, meaning each input x > 0 maps to exactly one output.
• Logarithmic Rules: Product Rule: $log_b(MN) = \log_b M + \log_b N$, Quotient Rule: $\log_b(M/N) = \log_b M - \log_b N$, and Power Rule: $\log_b(M^k) = k \log_b M$.

Common Logarithmic Bases

• Base 10: Used in pH levels and the Richter scale.
• Natural Base (e): Appears frequently in calculus, particularly in continuous growth rates.

Logarithm multifunction

When extending logarithms to the complex domain, the function becomes multi-valued. This arises because complex numbers are represented in polar form as: $z = r e^{i\theta}$ where:

• r = |z| > 0 is the modulus (a positive real number) representing its distance from the origin in the complex plane.
• $\theta = \arg(z)$ denotes the multi-valued set of all arguments of z that differ by multiples of 2π.

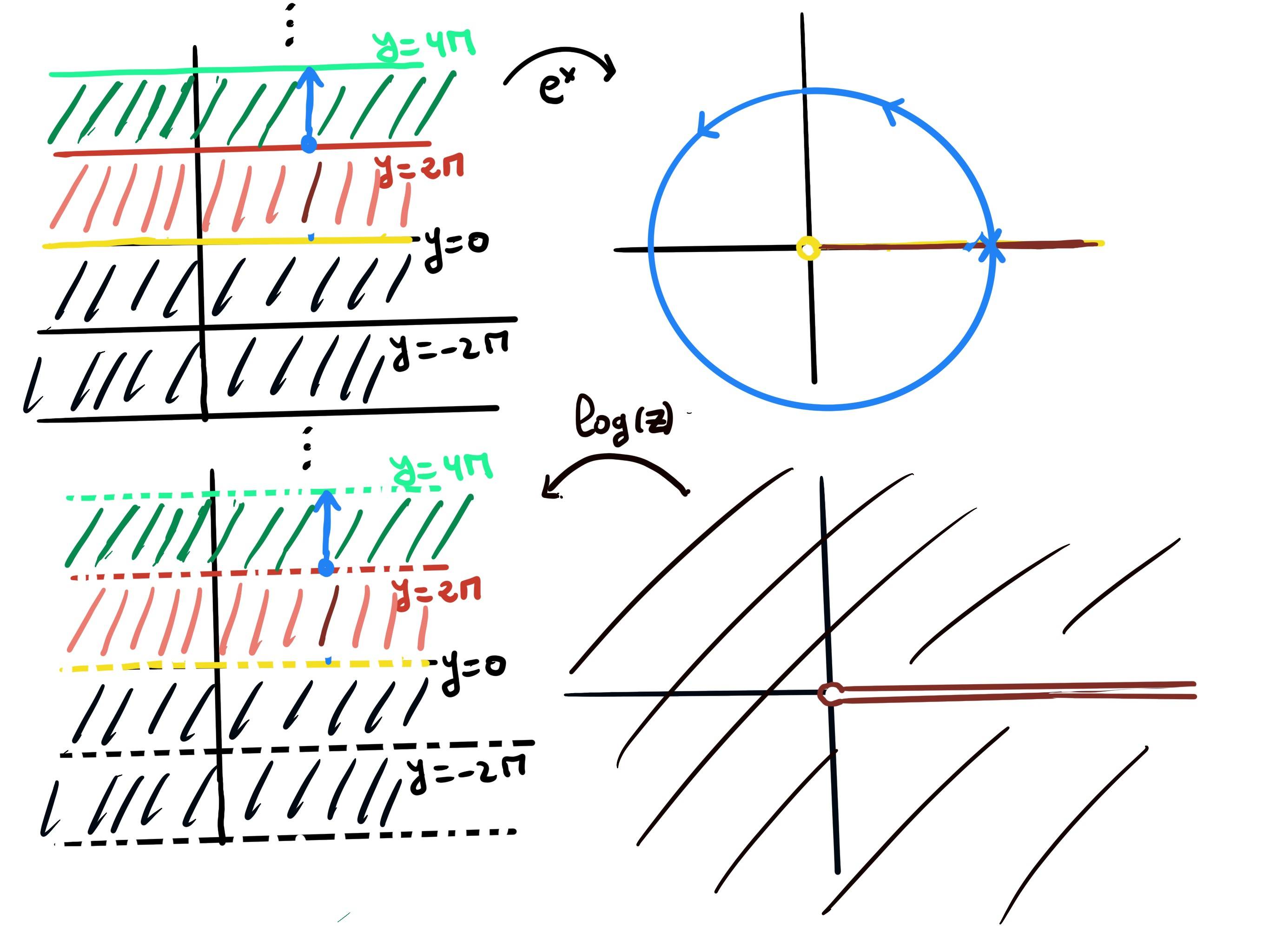
The multifunction nature arises because the argument arg(z) is not uniquely defined. For any integer k, adding $2\pi k$ to the argument gives another valid logarithm: $\log(z) = \ln|z| + i(\arg(z) + 2\pi k)$

Let z ∈ ℂ \ {0}. Consider the solutions to the equation $e^w = z$. We are always going to consider the base e.

If w = u + iv, $e^w = e^{u + iv} = e^u·e^{iv} = |z|e^{i\theta}$.

Hence, u = ln|z| and v ≡ θ (mod 2π), and realize that this expression is perfectly defined because |z| is strictly positive. Therefore, all solutions are w = ln|z| + i(θ + 2πk), i.e., w ∈ log(z).

Definition

For a non-zero complex number z, the complex logarithm is defined as the set: log(z) := ln|z| + i·θ, θ ∈ arg(z) where:

• |z| is the modulus of z, representing its distance from the origin in the complex plane.
• θ ∈ arg(z), arg(z) is the argument of z, representing the angle between the positive real axis and the line connecting the origin to z.

Any value of log(z) is a solution to $e^{log(z)} = z$, log(z) = {ln|z| + i(θ + 2πk) : θ ∈ arg(z), k ∈ ℤ} = {ln|z| + iθ : θ ∈ arg(z)} and z ≠ 0, where Arg(z) stands for single-valued choice of the argument (a branch), typically Arg: ℂ \ {0} → (-π, π].

Because the argument is multi-valued, the logarithm function is a multifunction. Since there is no continuous single-valued argument function on ℂ \ {0} → ℝ, therefore there is no continuous single-valued logarithm on all of ℂ \ {0}. The obstruction is topological (a loop around 0 changes the value by 2π).

Recall. A multifunction, also known as a multivalued function, is a mathematical object that assigns multiple values to each input. In other words, it’s a function that can have more than one output for a given input. Multifunctions are useful in modeling real-world phenomena where a single input can result in multiple possible outcomes.

A principal branch is any single-valued selection $Log_α(z) = ln|z| + i\Theta(z), \Theta(z) ∈ (α, α + 2\pi)$ defined on a simply connected cut domain ℂ \ {re^iα: r ≥ 0}

For any branch $Log_α$ we have $Im(Log_α​(z))=\Theta(z)∈(α,α+2π)$. Thus the image of the branch lies in the horizontal strip {u + iv: u∈R, v ∈ (α, α+2π)}.

A function fₖ : ℂ \ [0, ∞)→ ℂ given by fₖ(z) = log|z| + iθ(z) where θ(z) ∈ arg(z) and 2kπ < θ(z) < 2(k+1)π, k ∈ ℤ is called a brach of the logarithm multifunction. fₖ is continuous.

Geometric Mapping of the Exponential Function

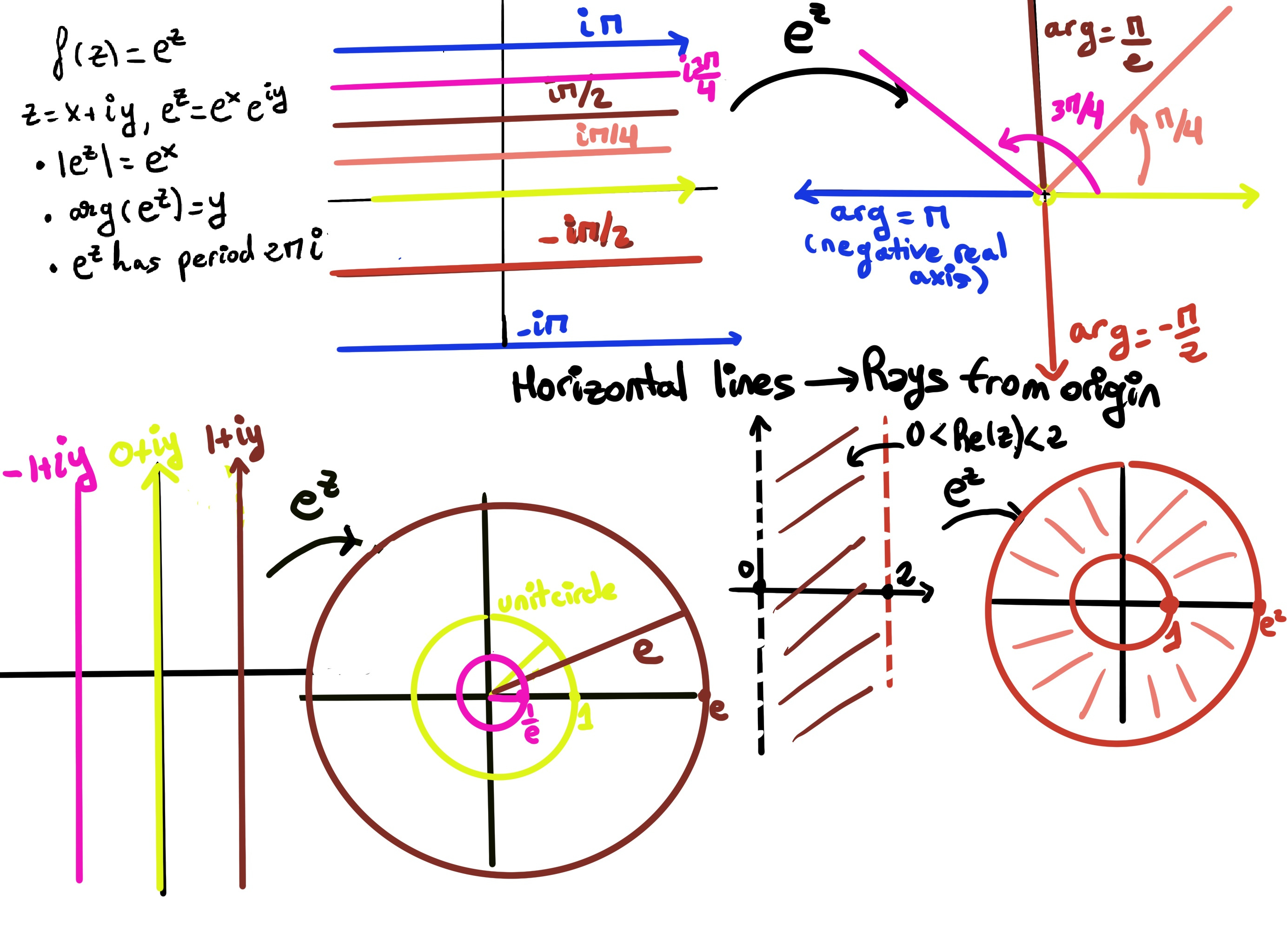
For z = x + iy, let’s analyze how the exponential $e^{z} = e^{x}(\cos y + i \sin y)$ transform the complex plane:

• Horizontal lines y = c (constant imaginary part): map to rays from the origin at angle $y = c \bmod 2\pi$, with varying radius $e^{x}$. In particular, y = 0, ±2π, ±4π, … map to the positive real axis.
• Vertical lines x = c (constant real part): map to circles centered at the origin with radius $e^{x}$, as the angle varies.
• The crucial observation is that the exponential function has period 2πi in the imaginary direction. Each horizontal strip 2nπ < y < 2(n+1)π of width 2π in the z-plane maps to the entire punctured complex plane ℂ \ [0, ∞). The boundaries y=2nπ all map to the positive real axis [0,∞).
• Branch Cut and Logarithm Definition: When you choose a specific strip 2nπ < y < 2(n+1)π. (1) The exponential map becomes bijective from this strip to ℂ ∖ [0,∞). (2) This allows us to define an inverse function (a branch of the logarithm) that is continuous and single-valued. (3) The positive real axis serves as the branch cut - the unavoidable discontinuity where the logarithm “jumps” between branches. A function fₖ : ℂ \ [0, ∞)→ ℂ given by fₖ(z) = log|z| + iθ(z) where θ(z) ∈ arg(z) and 2kπ < θ(z) < 2(k+1)π is called a branch of the logarithm.

Proposition. A function fₖ : ℂ \ [0, ∞)→ ℂ given by fₖ(z) = log|z| + iθ(z) where θ(z) ∈ arg(z) and 2kπ < θ(z) < 2(k+1)π, k ∈ ℤ is analytic.

Proof:

Let fₖ(z) = log|z| + iθ(z) where θ(z) ∈ arg(z), 2kπ < θ(z) < 2(k+1)π, and k ∈ ℤ.

The key insight is to use the fact that the logarithm is the inverse of the exponential function, i.e., on ℂ \ [0, ∞), $e^{f_k(z)} = z, h = (z + h) - z = e^{f_k(z+h)}-e^{f_k(z)}$.

Define the Derivative. We start with the limit definition of the derivative for fₖ(z). $f_k(z)^' = \lim_{h \to 0} \frac{f_k(z+h)-f_k(z)}{z+h-z} =[\text{Since fₖ is continuous (*)}] \lim_{f_k(z+h) \to f_k(z)} \frac{f_k(z+h)-f_k(z)}{e^{f_k(z+h)}-e^{f_k(z)}}$

We leverage the continuity of fₖ (*) to change the limit variables from h → 0 to fₖ(z+h) → fₖ(z) where h ∈ B(z; ε) ⊂ ℂ \ [0, ∞). This allows for the substitution p = $f_k(z+h)-f_k(z)$, where $p \to 0 \text{ as } f_k(z+h) \to f_k(z)$

Therefore, $\lim_{f_k(z+h) \to f_k(z)} \frac{f_k(z+h)-f_k(z)}{e^{f_k(z+h)}-e^{f_k(z)}} = \lim_{p \to 0} \frac{p}{e^{f_k(z)}(e^p -1)} = \frac{1}{e^{f_k(z)}}·lim_{p \to 0}\frac{p}{e^p -1} = \frac{1}{z}$. Since the fundamental limit $lim_{p \to 0}\frac{p}{e^p -1} = 1$ evaluates to 1.

This result holds for any z in the domain ℂ \ [0, ∞). Hence, fₖ is analytic at z ∈ ℂ \ [0, ∞) and $f_k^'(z) = \frac{1}{z}$.

Conclusion:

1. On a cut plane, ℂ ∖{$re^{iα}: r ≥ 0$}, i.e., the entire complex plane except for a ray (a “cut”) starting at the origin and extending to infinity at an angle α, we can define a single, continuous value for the argument θ for every point in the domain.
2. The function Log_α is the branch of the logarithm where the argument of z is restricted to the interval (α, α + 2π). Specifically: Log_α = ln|z| + iarg(z) where arg(z) ∈ (α, α + 2π).
3. Log_α is holomorphic and $\frac{d}{dz}Log_α(z) = \frac{1}{z}$.

Alternative Proof of Holomorphicity and the Derivative

1. Let w = Log_α(z). By the definition of our logarithm branch, this means z = e^w. The domain of w is the strip {u + iv ∣ v ∈ (α, α + 2π)}.
2. The function f(w) = e^w is holomorphic on the entire complex plane (it’s an entire function).
3. The derivative is f’(w) = $\frac{d}{dw}(e^w)$ = e^w. This derivative is never zero.
4. The inverse function theorem states that if f is holomorphic and f′(w) ≠ 0, then its inverse function f^-1(z) = Log_α(z) is also holomorphic.
5. Furthermore, the derivative of the inverse function is given by: $\frac{d}{dz}Log_{\alpha}(z) = \frac{1}{\frac{d}{dw}(e^w)} = \frac{1}{e^w} = \frac{1}{z}$ ∎