Tell me and I’ll forget; show me and I may remember; involve me and I’ll understand, Chinese Proverb

image info

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

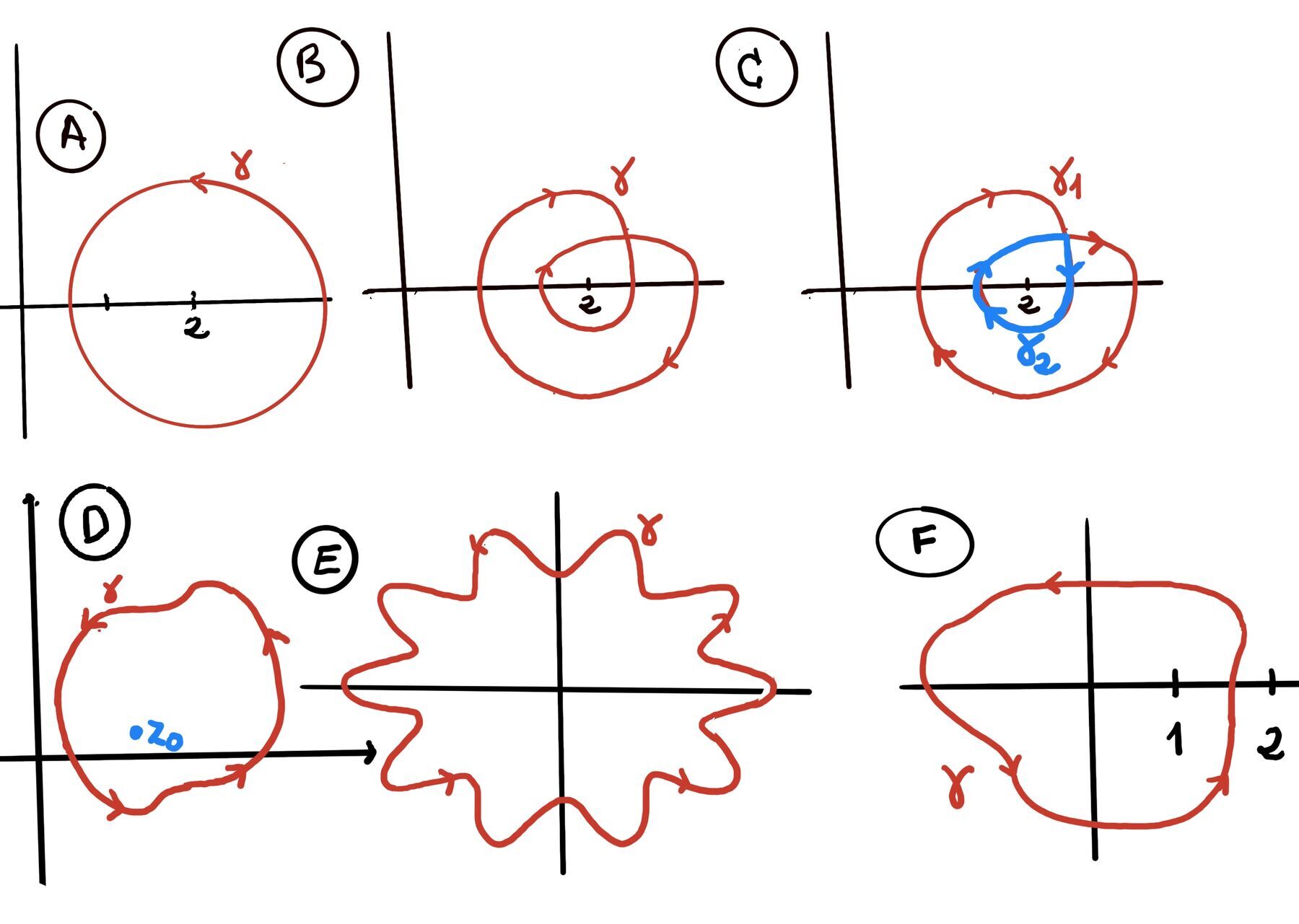
A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

In this definition, we integrate the function f along the path traced out by $\gamma(t)$. The term $\gamma^{'}(t)$ (the derivative of $\gamma$) accounts for the direction and speed of traversal along the path. This definition essentially transforms or converts the complex line integral into a regular real integral over the interval [a, b] via the parametrization $\gamma(t)$. The factor $\gamma'(t)dt = d\gamma$ represents an infinitesimal step along the curve, so $f(\gamma(t))\gamma'(t)dt$ is the infinitesimal contribution to the integral from that step.

Cauchy Integral Formula

Theorem. Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

Cauchy Integral Formula

It states that the value of an analytic function at any point z₀ is completely determined by the values the function takes on any simple closed curve that encircles the point. If you know the function’s values on the boundary, you know everything about the function’s behavior inside that boundary. This is quite unlike anything you’ve probably encountered with functions of real variables.

A more generalized version is as follows: $f^{(n)}(z_0) = \frac{n!}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz$.
Cauchy Integral Formula (Winding Number Lemma). Let γ be a closed rectifiable curve in ℂ, f analytic on an open set containing γ and its interior. For any point a not on γ, the Cauchy Integral Formula states: $\oint_{\gamma} \frac{f(z)}{z-a}dz = 2\pi i \cdot n(\gamma, a) \cdot f(a)$
The winding number is defined as $n(γ, a) = \frac{1}{2πi}\oint_\gamma \frac{dz}{z-a}$. This represents the net number of times γ winds around a counterclockwise.
For simple closed curves with positive orientation n(γ, a) = 1 if a is inside γ, 0 if outside.
For multiple windings n(γ, a) counts the net winding (e.g., 2 for two counterclockwise loops, -1 for one clockwise loop).
The formula reduces to the basic Cauchy Integral Formula when n(γ, a) = 1.
The formula can be used to calculate integrals: $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$
Key Conditions:
Analyticity: $ f(z) $ must be analytic (holomorphic) inside and on $\gamma$.
Contour $ C $: $\gamma$ is a simple closed curve (e.g., a circle, ellipse). A simple closed curve is a curve that has no self-intersections and is closed, meaning it starts and ends at the same point.
Point $z_0$: $z_0$ must lie inside $\gamma$. If $z_0$ is outside $\gamma$, the integral is zero.

Liouville’s Theorem

Liouville’s theorem emerges as a significant consequence of Cauchy’s Integral Formula.

Liouville’s Theorem. Let f be an entire function (analytic everywhere in the complex plane $\mathbb{C}$). If f is also bounded (meaning there exists a real number M > 0 such that $|f(z)| \le M$ for all $z \in \mathbb{C}$), then f must be a constant function..

Liouville’s theorem emerges as a significant consequence of Cauchy’s Integral Formula. This theorem is pivotal in establishing the non-existence of non-constant bounded entire functions and serves as a stepping stone for proving the fundamental theorem of algebra, which asserts that every non-constant, single-variable polynomial with complex coefficients has at least one complex root.

It shows that the requirement of analyticity everywhere imposes a severe constraint: non-constant growth is necessary for a non-constant function to be entire (e.g., f(z) = z or $f(z) = e^z$ are entire but unbounded).

Proof.

Let a, b ∈ ℂ any two distinct complex numbers. Define the simple closed contour γ(0; R) as the circle centered at the origin with radius R. We choose R large enough such that both a and b are strictly inside $\gamma(0; R)$. (i.e., $R > \max\{|a|, |b|\}$).

$$ \begin{aligned} |f(a) - f(b)| [\text{By the Cauchy's Integral Formula}] &=|\frac{1}{2\pi i}\oint_{\gamma(0; R)} \frac{f(z)}{z-a}dz - \frac{1}{2\pi i}\oint_{\gamma(0; R)} \frac{f(z)}{z-b}dz| \\[2pt] &[\text{Using linearity, we combine the integrals over the common contour }] \gamma: \\[2pt] &=|\frac{1}{2\pi i}\oint_{\gamma(0; R)} (\frac{f(z)}{z-a} - \frac{f(z)}{z-b})dz| \\[2pt] &[\text{Combine the terms inside the integral using a common denominator:}] \\[2pt] &=|\frac{1}{2\pi i} \oint_{\gamma(0; R)} \frac{f(z)(z-b)-f(z)(z-a)}{(z-a)(z-b)}dz| \\[2pt] &[\text{Factor out f(z) and simplify the numerator: }] f(z)[(z-b) - (z-a)] = f(z)[z - b - z + a] = f(z)(a - b) \\[2pt] &= |\frac{1}{2\pi i} \oint_{\gamma(0; R)} \frac{f(z)(a-b)}{(z-a)(z-b)}dz| \end{aligned} $$

For any point z on the circle |z| = R, the distance from z to a is bounded below by the distance R minus the distance |a| (by the Reverse Triangle Inequality),$|z-a| \ge | |z| - |a| | = R - |a|$. Therefore, |z - a| ≥ R - |a|, |z - b| ≥ R - |b| for all z ∈ γ(0; R)* (i)

By the ML-Estimation theorem. Remember that, $\left|\oint_{\gamma} h(z)dz\right| \le M L$, |i| = 1, $|\frac{1}{2\pi i}| = \frac{1}{2\pi}$, |a·b| = |a|·|b|, and f is bounded, ∃M s.t. |f(z)| ≥ M ∀z∈dom(f) = ℂ.

$$ \begin{aligned} |f(a) - f(b)| &\le \frac{1}{2\pi} \oint_{\gamma(0; R)} \frac{|f(z)||a-b|}{|z-a||z-b|}|dz| \\[2pt] &[\text{|a - b| is constant and can be factored out}]\\[2pt] &\le \frac{1}{2\pi}M|a-b| \oint_{\gamma(0; R)} \frac{1}{|z-a||z-b|}|dz| \\[2pt] &[\text{The length of the circle γ(0; R) is L = 2πR:}] \oint_{\gamma(0; R)} |dz| = 2\pi R \\[2pt] &\le[(i)] \frac{1}{2\pi}M|a-b|\frac{1}{(R - |a|)(R - |b|)}\cdot 2\pi R. \end{aligned} $$

Simplify by canceling $2\pi$, we get: $M|a-b| \frac{1}{(1 - \frac{|a|}{R})(R-|b|)}$, hence $|f(a) - f(b)| \le M|a-b| \frac{1}{(1 - \frac{|a|}{R})(R-|b|)}$.

So the LHS of the above inequality does not depend on R, but the RHS does. As $R \to \infin, 1 - \frac{|a|}{R} \to 1, R-|b| \to \infin$. In words, the RHS of the above inequality becomes arbitrarily small, hence the LHS is bounded by a quantity that approaches zero. Then, |f(a) - f(b)| = 0 ⟹ f(a) - f(b) = 0 ⟹ f(a) = f(b). Since a and $b$ were arbitrarily chosen complex numbers, the value of the function must be the same everywhere, meaning f(z) is a constant function. Q.E.D.

Fundamental Theorem of Algebra. Let p(z) be a non-constant polynomial with complex coefficients. Then, there exists at least one complex number a ∈ ℂ such that p(a) = 0. Consequently, a complex polynomial of degree $n \ge 1$ has exactly n roots (counting multiplicity) in ℂ.

The field of complex numbers ($\mathbb{C}$) is algebraically closed —you never have to leave $\mathbb{C}$ to find the roots of a complex polynomial.

Proof.

The proof uses contradiction. We assume the theorem is false (i.e., the polynomial has no roots in $\mathbb{C}$) and show that this assumption leads to a contradiction with Liouville’s Theorem.

Suppose the theorem is false. Assume that for a non-constant polynomial p(z), we have p(z) ≠ 0 for all z ∈ ℂ. Define a a new function f(z) as the reciprocal of p(z), f(z) = $\frac{1}{p(z)}$.

Since p(z) is a polynomial, it is entire (analytic everywhere). If our assumption holds ($p(z) \neq 0$ everywhere), f(z) is analytic on the entire complex plane.

To apply Liouville’s Theorem, we must prove that the entire function $f(z)$ is bounded, meaning $|f(z)| \le M$ for some constant M everywhere in $\mathbb{C}$.

Let p(z) be a polynomial of degree $n \ge 1: p(z) = c_n z^n + c_{n-1} z^{n-1} + \dots + c_0 \quad \text{where } c_n \neq 0$. For a non-constant polynomial, as $|z| \to \infty$, the highest power (leader) term ($c_n z^n$) dominates all others, $\lim_{|z| \to \infty} |p(z)| = \lim_{|z| \to \infty} |c_n z^n| = \infty$.

Since the magnitude of $p(z)$ goes to infinity, the magnitude of its reciprocal must go to zero: $\lim_{|z| \to \infty} |f(z)| = \lim_{|z| \to \infty} \left|\frac{1}{p(z)}\right| = 0$

By the limit definition, there must exist a sufficiently large radius R such that for all |z| > R, |f(z)| is very small. We can, for instance, guarantee that: $|f(z)| \le 1 \text{ for all } |z| > R$.

Consider the closed disk $\overline{B(0, R)} = \{z \in \mathbb{C} : |z| \le R\}$ (the interior region), this is a compact set in the complex plane (closed and bounded).

Since p(z) is non-zero and continuous on this compact set, $f(z) = \frac{1}{p(z)}$ is also continuous on this compact set ⇒[By the Extreme Value Theorem] f(z) must attain a maximum magnitude on this disk. Let this maximum be $M_{\text{inner}}, |f(z)| \le M_{\text{inner}} \text{ for all } |z| \le R$. Combining both results $|f(z)| \le M = max(1, M_{inner}) \text{ for all } z \in \mathbb{C}$. Thus, f(z) is a bounded entire function.

The Extreme Value Theorem states that a continuous complex-valued function on a nonempty compact subset (i.e., closed and bounded) of $\mathbb{C}$ attains its maximum and minimum modulus values.

Since f(z) is a bounded entire function, Liouville’s Theorem forces f(z) to be a constant: $f(z) = c \text{ for some constant } c \in \mathbb{C}$. Furthermore, since $f(z) = \frac{1}{p(z)}$, if f(z) is a constant c, then p(z) must also be a constant, p(z) = 1/c. This contradicts our initial assumption that p(z) is a non-constant polynomial, so there must exist at least one root $a \in \mathbb{C}$ such that p(a) = 0.

In algebra, the Factor Theorem says: If p(z) is a polynomial and p(a) = 0, then (z - a) is a factor of p(z).

Once we know that p(z) has at least one root, let’s name it $a_1$, the Factor Theorem states that we can write p(z) as: $p(z) = (z - a_1) \cdot q(z)$ where q(z) is a polynomial of degree n - 1. If q(z) is non-constant (i.e., if $n-1 \ge 1$), we apply the Factor Theorem again to q(z) to find a root $a_2$. We repeat this process n times until the remaining polynomial is a constant.

This process proves that a complex polynomial of degree n can be factored completely: $p(z) = c_n (z - a_1)(z - a_2)\cdots(z - a_n)$. Hence, a polynomial of degree $n \ge 1$ has exactly n roots (counting multiplicity) in the complex plane $\mathbb{C}$.

Exercises

Let f be an entire function (analytic everywhere) that satisfies a growth condition: |f(z)| ≤ M |z| for all z ∈ ℂ. (a) Show that all higher-order derivatives ($n \ge 2$) are zero everywhere, $\forall n \ge 2, f^{(n)}(z) = 0, \forall z$. (b) Demonstrate that f(z) is indeed a linear function in the complex plane of the form f(z) = az + b.

Solution.

Before we do anything else, let’s use the given condition at the point z = 0: |f(0)| ≤ M |0| ⇔ |f(0)| ≤ 0. Since the modulus (absolute value) of a complex number cannot be negative, the only possibility is that |f(0)| = 0, which means f(0) = 0.

Step 1. Define the Auxiliary Function g(z).

Since f is an entire function, f’(0) exists. Let’s define a new function, $g(x) = \begin{cases} \frac{f(z)}{z}, &z \ne 0 \\ f'(0), &z = 0 \end{cases}$

Step 2. Show g(z) is Entire.

For $z \ne 0$: f(z) is entire and $z$ is entire. Their quotient $\frac{f(z)}{z}$ is analytic everywhere except possibly at z = 0.
For z = 0: We need to check if g(z) is analytic at the origin. Since f(z) is entire and f(0) = 0, its Taylor series at z = 0 must look like: $f(z) = c_1 z + c_2 z^2 + c_3 z^3 + \dots$.
If f(z) is an entire function, it is analytic everywhere in the complex plane. Its Taylor series expansion around z=0 is: $f(z)=\sum _{n=0}^{\infty }c_nz^n$. The coefficients $c_k$ in the Taylor series of an entire function f(z) are given by $c_k=\frac{f^{(k)}(0)}{k!}$, where $f^{(k)}(0)$ is the k-th derivative of f evaluated at 0. Given that f(0) = 0, we have: $f(0)=c_0=0$ (the constant term in its Taylor series expansion around z = 0 must vanish). So the series becomes: $f(z)=c_1z+c_2z^2+c_3z^3+\dots $

So, for $z \ne 0, g(z) = \frac{f(z)}{z} = \frac{c_1 z + c_2 z^2 + c_3 z^3 + \dots}{z} = c_1 + c_2 z + c_3 z^2 + \dots$. This is a new power series that converges everywhere. By definition, g(0) = f’(0), and this is exactly $c_1 = \frac{f^{(1)}(0)}{0!} = \frac{f'(0)}{1}$, which is the value this power series takes at z = 0. Therefore, $g(z)$ is represented by a power series that converges everywhere, which means g(z) is an entire function.

Step 3. Show g(z) is Bounded.

$$\begin{aligned} \forall z \ne 0, &|g(z)| = |\frac{f(z)}{z}| \\[2pt] &= \frac{|f(z)|}{|z|} \\[2pt] &\le \frac{M|z||}{|z|} = M. \end{aligned} $$

For z = 0: The function g(z) is continuous, so its value at 0 must be consistent with the limit of its values nearby (the limit of |g(z)| as $z\rightarrow 0$). Since $|g(z)| \le M$ for all $z \ne 0$, it must be that the limit of |g(z)| as $z\rightarrow 0$ must also be less than or equal to M. Therefore, $|g(0)|=\left| \lim _{z\rightarrow 0}g(z)\right| \leq \limsup _{z\rightarrow 0}|g(z)|\leq M$. Thus, $|g(z)| \le M$ for all $z \in \mathbb{C}$.

Step 4: Apply Liouville’s Theorem.

We have an entire function g(z) that is also bounded. Liouville’s Theorem states that any bounded entire function must be a constant. Therefore, $g(z) = a$ for some constant $a \in \mathbb{C}$.

Since $g(z) = \frac{f(z)}{z} = a$, we have f(z) = az. This is obviously of the form f(z) = az + b where b = 0 (Part b).

If $f(z)=az$, then $f''(z)=0$, so $f^{(n)}(z)=0$ for all $n \ge 2$ (Part a)

Let $u: \mathbb{C} \rightarrow \mathbb{R}$ be a bounded harmonic function and suppose that u is a real apart of some analytic function f on all of the complex plane ℂ (f is entire). Then, show that us is constant.

Solution

Our main tool will be Liouville’s Theorem, which states that any function that is both entire and bounded must be a constant. The problem is that we are told u is bounded, not f. The idea or strategy is to construct a new auxiliary function that we can prove is both entire and bounded.

Consider the function $g(z) = e^{f(z)}$. Since f is entire (analytic everywhere), $e^f$ is entire (the composite of two entire functions is always entire), too.

$|e^{f(z)}| = e^{Re(f(z))} = e^{u(z)} \le e^M$ (u is a bounded function, this means there exist some positive real number M such that $|u(z)| \le M$ for all $z \in \mathbb{C}$, and the exponential is an increasing function). Note: $\forall w \in \mathbb{C}, w = u + iv$. Then, $|e^w| = |e^{u+iv}| = |e^u \cdot e^{iv}| = |e^u| \cdot |e^{iv}| =[\text{Since u is real and } |e^{iv}| = |\cos(v) + i\sin(v)| = \sqrt{\cos^2(v) + \sin^2(v)} = 1] e^u$

Therefore, g(z) is both entire and bounded over the entire complex plane. By Liouville’s theorem, $g(z) = e^{f(z)}$ is a constant function, $g(z) = e^{f(z)} = c$ where c is a constant. Then, $|e^{f(z)}| = |c| \leadsto e^{u(z)} = |c|$

Since |c| is a positive constant, we can take the natural logarithm of both si des to solve for u(z), u(z) = ln(|c|). Since ln(|c|) is just a fixed real number, we have proven that u(z) is constant for all $z \in \mathbb{C}$.