Hyperbolic Functions (Real & Complex): A Step-by-Step Guide

As long as algebra is taught in school, there will be prayer in school, Cokie Roberts

Introduction

Hyperbolic functions are a set of mathematical functions that resemble or mirror many features of the trigonometric functions but arise from the geometry of hyperbolas rather than circles. They are essential in various fields, including calculus, differential equations, special relativity, complex analysis, and more.

Hyperbolic functions are defined using exponential functions $e^x$ and $e^{-x}$. The six primary hyperbolic functions are: Sine Hyperbolic (sinh): $\sinh(x) = \frac{e^x - e^{-x}}{2}$; Cosine Hyperbolic (cosh): $\cosh(x) = \frac{e^x + e^{-x}}{2}$; Tangent Hyperbolic (tanh): $\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$. Reciprocal functions. Sech (secant hyperbolic): $ \text{sech}(x) = \frac{1}{\cosh(x)}$; Csch (cosecant hyperbolic): $\text{csch}(x) = \frac{1}{\sinh(x)}$, Coth (cotangent hyperbolic): $\coth(x) = \frac{\cosh(x)}{\sinh(x)} = \frac{e^x + e^{-x}}{e^x - e^{-x}}$

Properties

• Fundamental Identity: $\cosh^2(x) - \sinh^2(x)= 1$ (all x ∈ ℝ).
• Pythagorean-Like Identities: $1 - \tanh^2(x) = \text{sech}^2(x), \coth^2(x) - 1 = \text{csch}^2(x)$.
• Parity: sinh(−x) = −sinhx (odd), cosh(−x) = coshx (even). Consequently tanh is odd; sech is even; csch and coth are odd.
• Addition, subtraction, and double-angle formulas: $\sinh(a\pm b) = \sinh a\cosh b\pm \cosh a\sinh b, \cosh(a\pm b) = \cosh a\cosh b\pm \sinh a\sinh b, \tanh(a\pm b) = \frac{\tanh a\pm \tanh b}{1\pm \tanh a \tanh b}.$ Special cases: $\sinh(2x)=2\sinh x \cosh x, \cosh(2x)=\cosh^2 x+\sinh^2 x$.
• Series expansions (about 0): $\boxed{\sinh x=\sum_{n=0}^\infty \frac{x^{2n+1}}{(2n+1)!}}, \boxed{\cosh x=\sum_{n=0}^\infty \frac{x^{2n}}{(2n)!}}$. Thus, sinh⁡ is odd and cosh is even; both series converge for all $x\in\mathbb{R}$.
• Derivatives: $ \frac{d}{dx} \sinh(x) = \cosh(x), \frac{d}{dx} \cosh(x) = \sinh(x), \frac{d}{dx} \tanh(x) = sech^2(x) = 1 - \tanh^2(x)$.
• Integrals: $\int \sinh(x) dx = \cosh(x) + C, \int \cosh(x) dx = \sinh(x) + C, \int \text{sech}^2(x) dx = \tanh(x) + C$.
• Differential equations sinh′′x = sinhx, cosh′′x = coshx, so sinh and cosh solve the linear second-order homogeneous differential equation y′′ = y with different initial conditions: sinh0 = 0, sinh′0 = 1; cosh0 = 1, cosh′0 = 0.

  Any solution to y’’ = y can be written as: $y(x) = A \cosh x + B \sinh x$ for constants $A, B \in \mathbb{R}$. This is analogous to the trigonometric case for y’’ = -y, where: sin x and cos x solve the equation.

• Graphs, monotonicity, asymptotics. The graphs of hyperbolic functions are similar to those of trigonometric functions, but they have some distinct differences.

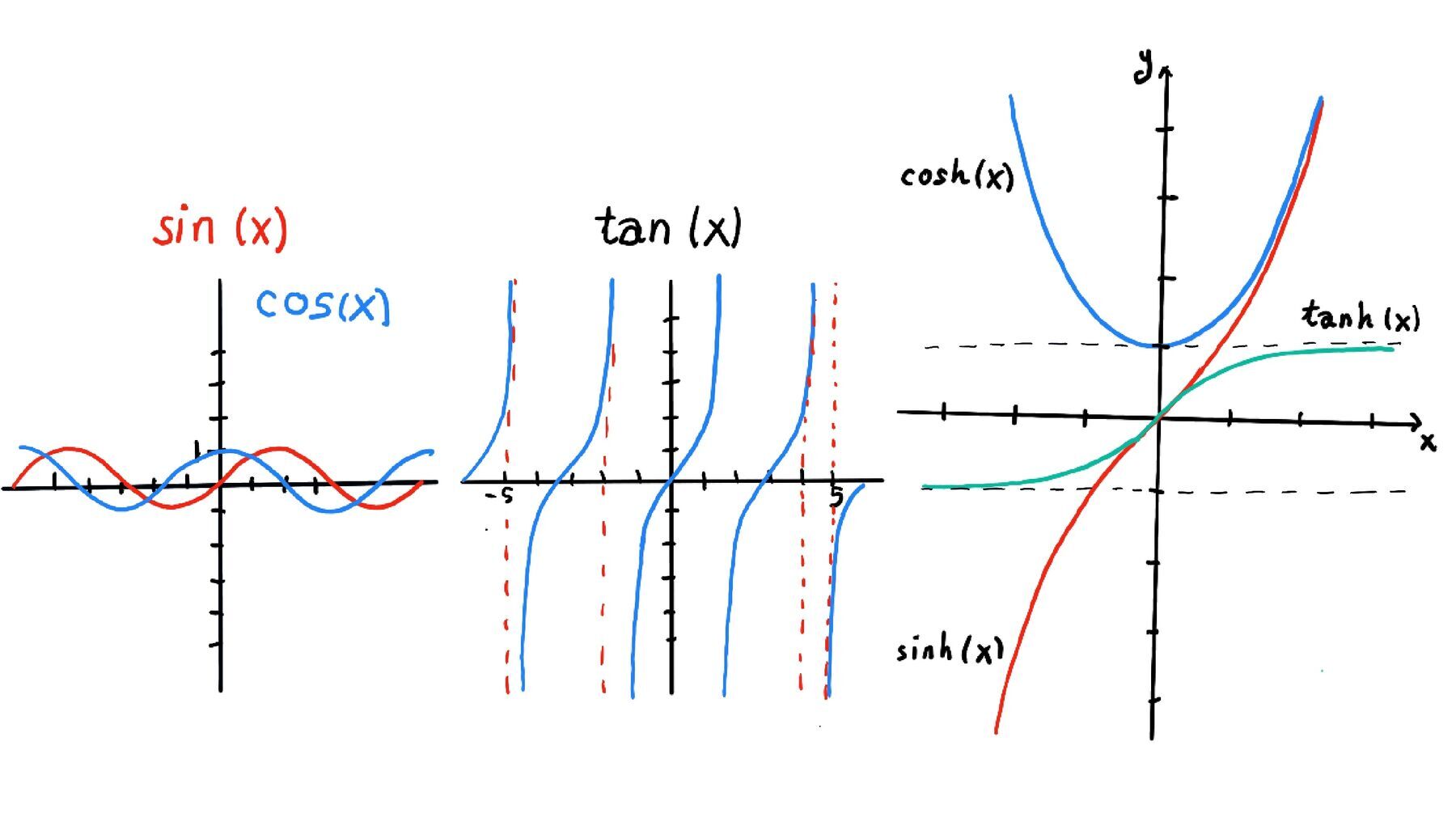
The graph of y = sinh(x) passes through the origin (sinh(0) = 0). It is strictly increasing and unbounded. As $x \to \pm\infty, \sinh(x) \sim \frac{1}{2} e^{x}$ and $\sinh(x) \sim -\frac{1}{2} e^{-x}$.

The graph of y = cosh(x) has a unique minimum at (0, 1), cosh(x) ≥ 1 and increases exponentially in both directions (away from the origin). As ∣x∣→∞ (it’s an even function), $\cosh(x)\sim \frac{1}{2} e^{|x|}.$

tanh(x) is strictly increasing with horizontal asymptotes ±1; $\lim_{x \to \pm\infty}\tanh(x) = \pm 1.$

• Inverse hyperbolic functions (definitions, domains, derivatives) For real x, $\mathbb{arsinh}(x)=\ln\bigl(x+\sqrt{x^2+1}\bigr)\quad(\text{all }x), \mathbb{arcosh}(x) = \ln\bigl(x+\sqrt{x^2-1}\bigr)\quad(x\ge 1), \mathbb{artanh}(⁡x) = \frac{1}{2}ln\left(\frac{1+x}{1-x}\right)\quad(|x|<1)$

Derivatives: $\frac{d}{dx}\mathbb{arsinh}(x) = \frac{1}{\sqrt{x^2+1}}, \frac{d}{dx}\mathbb{arcosh}(x) = \frac{1}{\sqrt{x-1}\sqrt{x+1}}, \frac{d}{dx}\mathbb{artanh}(x) = \frac{1}{1-x^2}.$

Examples: sinh(2) = (e^2 - e^-2) / 2 ≈ 3.63. Solve the equation cosh(x) = 2: cosh(x) = 2 => x = ± arccosh(2) = $\pm\ln(2+\sqrt{3})\approx \pm 1.31696.$

Complex Hyperbolic functions

Hyperbolic functions are analogs of trigonometric functions (sine, cosine, etc.), but they are defined using the exponential function and relate to the geometry of a hyperbola rather than a circle. When extended to complex analysis, these functions exhibit fascinating properties, periodicity, and applications in physics, engineering, and pure mathematics.

The hyperbolic sine (sinh), hyperbolic cosine (cosh), and other related functions are defined using the exponential function $e^z$, where z is a complex number. For a complex variable z = x + iy, the definitions are:

$cosh(z) = \frac{e^z + e^{-z}}{2}, sinh(z) = \frac{e^z - e^{-z}}{2}, \tanh(z) = \frac{\sinh(z)}{\cosh(z)} = \frac{e^z - e^{-z}}{e^z + e^{-z}}$

Hyperbolic Cotangent: $\coth(z) = \frac{\cosh(z)}{\sinh(z)}$, Hyperbolic Secant: $sech(z) = \frac{1}{\cosh(z)}$, Hyperbolic Cosecant: $csch(z) = \frac{1}{\sinh(z)}$

Properties

• Entire Functions. sinh(z) and cosh(z) are entire, meaning they are analytic (differentiable) everywhere in the complex plane. This is because $e^z$ is entire, and the operations in their definitions (addition, subtraction, division) preserve analyticity.
• Zeros: sinh(⁡z) = 0  ⟺  z=iπk, k ∈ ℤ; cosh⁡(z) = 0  ⟺ $z = i\Bigl(\frac{\pi}{2}+\pi k\Bigr), k\in\mathbb{Z}$.
• tanh is not entire. $tanh(⁡z) = \frac{\sinh z}{\cosh z}$ is meromorphic (a function that is holomorphic on all of its domain except for a set of isolated points, which are poles of the function) with simple poles at the zeros of cosh(⁡z), i.e. $z = i\Bigl(\frac{\pi}{2}+\pi k\Bigr)$ Likewise,
• Hyperbolic identity: cosh⁡²(z) − sinh²(z)=1 (analogous to cos²(z) + sin²(z)=1).
• Periodicity. Hyperbolic functions like sinh (x), cosh (x), and tanh (x) do indeed exhibit periodic behavior in the imaginary direction, and the period is $2\pi i$, e.g., $\cosh(z + 2\pi i) = \frac{e^{z + 2\pi i} + e^{-z - 2\pi i}}{2} = \frac{e^z e^{2\pi i} + e^{-z} e^{-2\pi i}}{2} =[\text{Since } e^{2\pi i} = e^{-2\pi i} = 1] = \frac{e^z + e^{-z}}{2} = \cosh(z)$
• Symmetry. Even/Odd Properties: $\sinh(-z) = -\sinh(z) \text{( odd function)}, \cosh(-z) = \cosh(z) \text{( even function)}$. These mirror the parity of sine and cosine in trigonometry.
• Relationship Between Hyperbolic and Trigonometric Functions. Since we know, $cos(z) = \frac{e^{iz} + e^{-iz}}{2}, cosh(iz) = cos(z), cosh(y) = cos(iy)$. Since we know, $sin(z) = \frac{e^{iz} - e^{-iz}}{2i}, sinh(iz) = isin(z), isinh(y) = sin(iy).$ cos(z) = cosh(iz), sin(z) = -isinh(iz), cosh(z) = cos(iz), sinh(z) = −isin(iz).
• Derivatives: $\frac{d}{dz}(cosh(z)) = sinh(z), \frac{d}{dz}(sinh(z)) = cosh(z), \frac{d}{dz}(\tanh(z)) = 1 - \tanh^2(z)$.

cos(x + iy) =[Angle Addition Formula: cos(A + B) = cos(A)cos(B) − sin(A)sin(B). Applying this to z = x+ iy, we let A = x and B = iy:] cos(x)cos(iy) -sin(x)sin(iy) =[Now we substitute cos(iy) = cosh(y) and sin(iy) = isinh(y)] cos(x)cosh(y) - isin(x)sinh(y).

• Addition formulas: $\cosh(z_1 + z_2) = \cosh(z_1)\cosh(z_2) + \sinh(z_1)\sinh(z_2), \sinh(z_1 + z_2) = \sinh(z_1)\cosh(z_2) + \cosh(z_1)\sinh(z_2). \sinh(2z) = 2\sinh(z)\cosh(z), \cosh(2z) = \cosh^2(z) + \sinh^2(z)$.

• For complex argument z = x + iy: $\cosh(x + iy) = \cosh(x)\cos(y) + i\sinh(x)\sin(y), \sinh(x + iy) = \sinh(x)\cos(y) + i\cosh(x)\sin(y)$

• Taylor series expansion. Hyperbolic functions are entire functions (analytic everywhere in the complex plane), and their Taylor series around z = 0 are: $\sinh z = z + \frac{z^3}{3!} + \frac{z^5}{5!} + \frac{z^7}{7!} + \dots = \sum_{n=0}^{\infty}\frac{z^{2n+1}}{(2n+1)!}, \cosh z = 1 + \frac{z^2}{2!} + \frac{z^4}{4!} + \frac{z^6}{6!} + \dots = \sum_{n=0}^{\infty}\frac{z^{2n}}{(2n)!}$