Gauss-Lucas Theorem and Convex Hulls in Complex Analysis

It always seems impossible until its done, Theodor Seuss Geisel

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

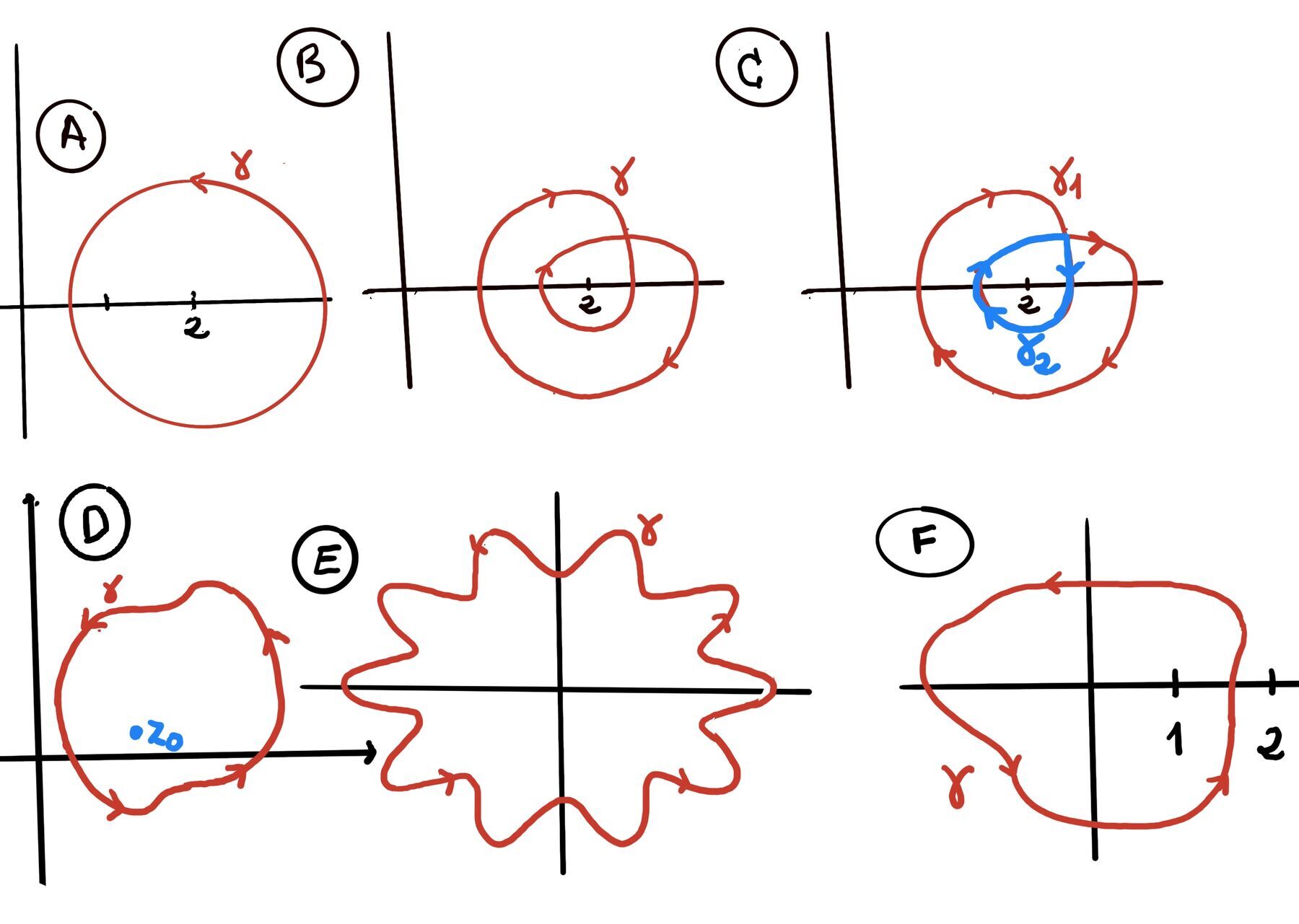
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

Convex Sets and Convex Hulls

Definition. A set $𝐾 \subset \mathbb{C}$ is said to be convex if, for any two points $z_1, z_2 \in K$, and for any real parameter t with $0 \leq t \leq 1$, the point $z_t = (1-t)z_1 + t z_2$ also belongs to K; equivalently, the entire straight line segment connecting any two points in K lies within K. Geometrically, this property excludes “indentations” (or concave regions where the boundary of the set bends inwards, e.g., a crescent shape where a line segment drawn between two points on its inner arc would lie mostly outside the crescent) and “holes” (Figure ii).

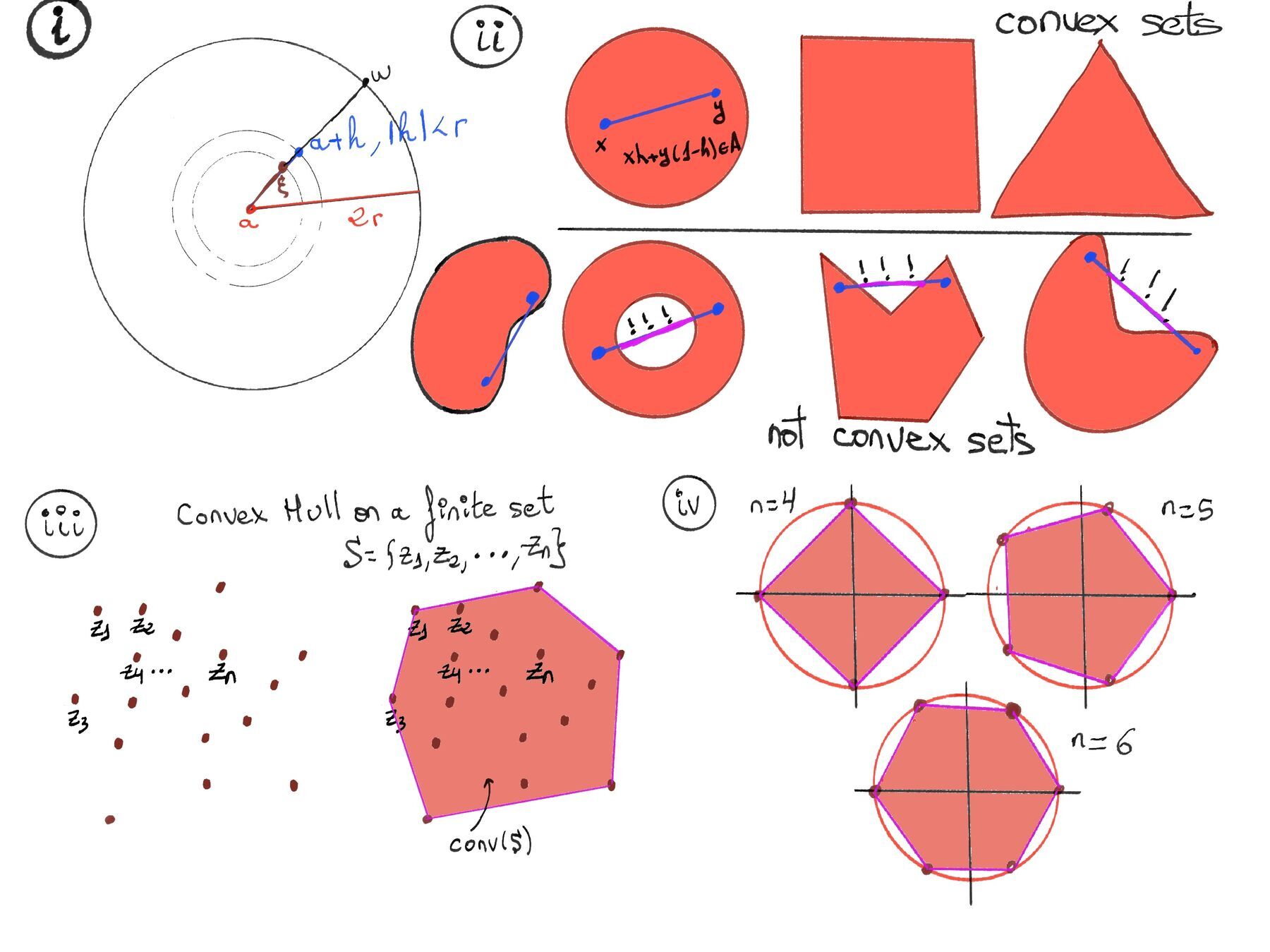
Examples are line segments ($\forall z_1, z_2 \in \mathbb{C}, L[z_1, z_2] = { (1-t)z_1 + t z_2 : t \in [0,1] }$), triangles (let $z_1, z_2, z_3 \in \mathbb{C}$ be three non-collinear points. The triangle with vertices $z_1, z_2, z_3 $ is the set $T[z_1, z_2, z_3] = { t_1 z_1 + t_2 z_2 + t_3 z_3: t_i \geq 0, t_1 + t_2 + t_3 = 1}$ and contains all convex combinations of its vertices, i.e., all points inside the triangle including its interior and boundary), regular polygons (a regular (n)-gon inscribed in the complex plane is defined by its vertices $z_k = e^{\frac{2\pi i k}{n}}, k = 0, 1, \dots, n-1$ after possible scaling and translation. The closed regular polygon consists of all points that are convex combinations of the vertices. If we include the interior and boundary, the regular polygon is a compact convex set), disks (e.g., the closed unit disk D = {$z \in \mathbb{C} : |z| \leq 1$} is convex), and ellipses.

Definition. Given a set $K \subset \mathbb{C}$ its convex hull, denoted conv(K) or co(K), is defined in several equivalent ways:

• A convex set $S \subset \mathbb{C}$ containing K such that no proper convex subset of S contains K, i.e., the unique smallest convex set containing K.
• The convex hull is the intersection of all convex sets containing K, $conv(K) := \bigcap{C: C \textrm{ is convex and } K \subseteq C }$. This guarantees both minimality (it is contained in any convex set containing K) and uniqueness (no smaller convex set containing K exists).
• The convex hull is the set of all finite convex combinations of points in K, $conv(K) := {\sum_{i=1}^n \lambda_i z_i : n \geq 1, z_i \in K, \lambda_i \geq 0, \sum_{i=1}^n \lambda_i = 1}$. Every convex combination is a weighted average, with nonnegative weights summing to one.
• Every point inside the convex hull in $\mathbb{C} \simeq \mathbb{R}^2$ can be written as a convex combination of at most three points in K. Geometrically, this means any point inside the convex hull (which is a convex polygon for a finite set of points, or a general convex set for an infinite set) lies within a triangle whose vertices are points from the original set 𝐾.

This is an application of Carathéodory’s Theorem in the complex plane, ℂ, which is geometrically equivalent to the 2-dimensional Euclidean space, ℝ². It states that if if a point 𝑥 lies in the convex hull of a set 𝐾 in a 𝑑-dimensional Euclidean space (ℝᵈ), then 𝑥 can be written as a convex combination of at most 𝑑 + 1 points in 𝐾..

Applying Carathéodory’s theorem for 𝑑 = 2. Thus, any point in the convex hull of a set 𝐾 in ℂ can be written as a convex combination of at most three points in 𝐾.

Properties of Convex Sets and Convex Hulls

1. By construction, the convex hull is minimal among all convex supersets of K (no proper subset of conv(K) that contains K is convex) and unique.

2. These definitions are equivalent.

3. Intersection of Convex Sets is Convex. If $ {C_i}, i \in I$ is any (possibly infinite) family of convex subsets of $\mathbb{C}$, then $\bigcap_{i \in I} C_i$ is convex. Proof: For any $x, y \in \bigcap_{i \in I} C_i$, we have $x, y \in C_i$ for all i. Each $C_i$ being convex implies that for any $t \in [0,1], (1-t)x + t y \in C_i$. Thus, $(1-t)x+t y \in \bigcap_{i \in I} C_i$.

4. The convex hull construction is a closure operator because it satisfies the three defining properties of such an operator:
   Extensivity: For any set 𝑆 ⊆ Conv(𝑆), The original set 𝑆 is always contained within its own convex hull. The convex hull is the smallest convex set that contains 𝑆, so it must contain all elements of S.
   Monotonicity. If 𝑆 ⊆ 𝑇, then Conv(𝑆) ⊆ Conv(𝑇). If one set 𝑆 is a subset of another set 𝑇, then the smallest convex set containing 𝑆 must be a subset of the smallest convex set containing 𝑇.
   Idempotence. Conv(Conv(𝑆)) = Conv(𝑆). If you take the convex hull of a set that is already convex (the result of the first application of the operator), the operation does nothing further. The result remains the same convex set.

5. For a finite set $S = {z_1, z_2, ..., z_n} \subseteq \mathbb{C}$, the convex hull is the unique convex polygon whose vertices are in S and which encloses all points of S (Figure iii), e.g., for a singleton, the point itself; for collinear points, the line segment defined by the two outermost points (the “minimum” and “maximum” points along that line); for three points (Non-collinear, the three points form a triangle), the triangle including its interior; for n points, non-collinear, a convex m-gon where $3 \leq m \leq n$ where m is the number of extreme points (vertices, the points that form the boundary of the hull). Imagine $z_1, z_2, ..., z_n$ as nails in a wooden board. The convex hull is the shape formed by the smallest rubber band that you can stretch around all the nails.

6. A point w is a convex combination of points $z_1, ..., z_n$ if $w = \sum_{i=1}^n \lambda_i z_i, \lambda_i \geq 0, \sum_{i=1}^n \lambda_i = 1.$ By definition, a set is convex if and only if it contains every convex combination of its points. Convex combinations generalize the notion of “points between” $z_1$ and $z_2$ to higher cardinalities. For n = 2, convex combinations trace the straight line segment between them; for n = 3, all points inside and on the triangle formed by these three non-collinear points or vertices; for n = k, the interior of the (k-1)-simplex (the convex hull of 𝑘 affinely independent points) with those vertices.

Gauss-Lucas Theorem

Gauss-Lucas Theorem. Let $z_1, z_2, \cdots, z_n$ be the zeros of a polynomial P(z). Show that the zeroes of the derivative of P(z) lie within the convex hall of the points $z_1, z_2, \cdots, z_n$ in the complex plane. It states that the critical points of a polynomial (the zeros of its derivative P’) must lie within the convex hull of the polynomial’s roots (the zeros of P).

If we imagine the zeros as nails in a wooden board, the convex hull is the shape formed by the smallest rubber band that you can stretch around all these nails. Gauss-Lucas Theorem says that any root of P’(z) must be inside or on the boundary of this rubber band shape.

Solution.

Case 1: $\alpha$ is also a zero of $P(z)$. If α is one of the zeros of P(z), it means $\alpha = z_k$ for some k, then α (it is one of the nails of the wooden board) obviously lies in the convex hall of $z_1, z_2, \cdots, z_n$ in the complex plane and the theorem holds.

Case 2: $\alpha$ is not a zero of $P(z)$, P(α) ≠ 0. This means $\alpha$ is not one of the roots $z_1, \dots, z_n$.

Factor the polynomial. Since $z_1, \dots, z_n$ are the roots of $P(z)$, we can factor it as: $P(z) = c(z-z_1)(z-z_2)\cdots(z-z_n)$ where c is a non-zero complex constant.

Use Logarithmic Differentiation. We take the natural logarithm of both sides, $\ln P(z) = \ln c + \ln(z-z_1) + \ln(z-z_2) + \dots + \ln(z-z_n)$, and differentiate both sides with respect to z: $\frac{P'(z)}{P(z)} = 0 + \frac{1}{z-z_1} + \frac{1}{z-z_2} + \dots + \frac{1}{z-z_n}$

Let’s use the fact that $\alpha$ is a zero of $P'(z)$ and plug $z=\alpha$ into the previous formula, we get: $\frac{P'(\alpha)}{P(\alpha)} = \sum_{k=1}^n \frac{1}{\alpha-z_k}$.

Since $P'(\alpha) = 0$ and $P(\alpha) \neq 0$, the left side is zero: $\sum_{k=1}^n \frac{1}{\alpha-z_k} = 0$ (🚀)

We want to isolate $\alpha$, but it’s stuck in the denominators. We can make the denominators real by multiplying the top and bottom of each term by its complex conjugate: $\frac{1}{\alpha-z_k} = \frac{\overline{\alpha-z_k}}{(\alpha-z_k)\overline{(\alpha-z_k)}} = \frac{\bar{\alpha}-\bar{z_k}}{|\alpha-z_k|^2}$

Then, substitute this back into our equation (🚀): $\sum_{k=1}^n \frac{\bar{\alpha}-\bar{z_k}}{|\alpha-z_k|^2} = 0$

Isolate $\bar{\alpha}$. Let’s split the sum into two parts:

$$ \begin{aligned} \sum_{k=1}^n \frac{\bar{\alpha}}{|\alpha-z_k|^2} - \sum_{k=1}^n \frac{\bar{z_k}}{|\alpha-z_k|^2} &= 0 \\[2pt] \text{Moving the second sum to the other side} \\[2pt] \sum_{k=1}^n \frac{\bar{\alpha}}{|\alpha-z_k|^2} = \sum_{k=1}^n \frac{\bar{z_k}}{|\alpha-z_k|^2}\\[2pt] \text{Factoring } \bar{\alpha} \text{ out of the left sum (it's a constant):} \\[2pt] \bar{\alpha} \left( \sum_{k=1}^n \frac{1}{|\alpha-z_k|^2} \right) = \sum_{k=1}^n \frac{\bar{z_k}}{|\alpha-z_k|^2} \end{aligned} $$

Define two positive real numbers. $A_k = \frac{1}{|\alpha -z_k|^2}$. Since $\alpha \neq z_k$ (Case 2: α is not a zero of P(z)), the denominator is never zero. This means $A_k$ is a positive real number. Let’s also define $A = \sum_{k=1}^n A_k$. Since A is a sum of positive real numbers, A is also a positive real number.

Now, we want to substitute $A_k$ and $A$ back into our equation $\bar{\alpha} \left( \sum_{k=1}^n \frac{1}{|\alpha-z_k|^2} \right) = \sum_{k=1}^n \frac{\bar{z_k}}{|\alpha-z_k|^2}$ and we get: $\bar{\alpha} \left( \sum_{k=1}^n A_k \right) = \sum_{k=1}^n A_k \bar{z_k} \leadsto \bar{\alpha} A = \sum_{k=1}^n A_k \bar{z_k}$

We can now solve for $\bar{\alpha}, \bar{\alpha} = \frac{\sum_{k=1}^n A_k \bar{z_k}}{A} = \sum_{k=1}^n \left( \frac{A_k}{A} \right) \bar{z_k}$

Calculate $\alpha$ and show it’s a convex combination of $z_1, z_2, \cdots z_n$. We just take the complex conjugate of the entire equation: $\overline{(\bar{\alpha})} = \overline{\sum_{k=1}^n \left( \frac{A_k}{A} \right) \bar{z_k}} \leadsto \alpha = \sum_{k=1}^n \overline{\left( \frac{A_k}{A} \right)} \cdot \overline{(\bar{z_k})}$

The coefficients $\frac{A_k}{A}$ are real numbers (a positive real divided by a positive real). The conjugate of a real number is itself. Since, the conjugate of a conjugate complex number is the original complex number itself, the conjugate of $\bar{z_k}$ is just $z_k$.

So, the equation simplifies to: $\alpha = \sum_{k=1}^n \left( \frac{A_k}{A} \right) z_k$

In other words, $\alpha$ is a convex combination (a weighted average where all weights $c_k = \frac{A_k}{A}$ are positive and sum to 1) of the roots $z_1, \cdots, c_n$ and therefore, $\alpha$ must lie within their convex hull.

1. We know $A_k > 0$ and $A > 0$, so $c_k = \frac{A_k}{A} > 0$ (weights are positive).
2. $\sum_{k=1}^n c_k = \sum_{k=1}^n \frac{A_k}{A} = \frac{1}{A} \sum_{k=1}^n A_k = \frac{1}{A} \cdot (A) = 1$ (weights sum to 1).

• Show that all zeros (roots) of the polynomial $P(z) = 1 + 2z + 3z^2 + \cdots + nz^{n-1}$ are located inside the closed unit disk $\overline{B(0; 1)}, |z| \le 1$.

Solution:

Let’s define a new polynomial, $Q(z), Q(z) = z + z^2 + z^3 + \cdots + z^n$. Now, let’s compute its derivative, $Q'(z) = \frac{d}{dz} (z + z^2 + \cdots + z^n) = 1 + 2z + 3z^2 + \cdots + nz^{n-1} = P(z)$

We want to use the Gauss-Lucas Theorem, but first, we need to find all the zeros (our so called nails in our imaginary wooden board) of Q(z).

We can find the roots by factoring $Q(z), Q(z) = z(1 + z + z^2 + \cdots + z^{n-1})$. There are two sets of roots: z = 0 and the solutions to $1 + z + z^2 + \cdots + z^{n-1} = 0$. This is a geometric series. We know the formula for its sum: $1 + z + z^2 + \cdots + z^{n-1} = \frac{z^n - 1}{z - 1}$

So, we need to solve $\frac{z^n - 1}{z - 1} = 0$. This is true if and only if $z^n - 1 = 0$ (the n-th roots of unity), as long as $z - 1 \neq 0$ (i.e., $z \neq 1$, so we need to exclude the real root 1).

Therefore, the set of all zeros for $Q(z)$ is: {0, $ξ_k = e^{\frac{2\pi i k}{n}}, 1 \le k \le n - 1$} (Figure iv, n-th roots of unity and convex hull, n = 3, 4, and 5). The set of n - 1 points are all located on the unit circle (since $|e^{i\theta}| = 1$).

The Gauss-Lucas Theorem states that the zeros of the derivative P(z) = Q’(z) must lie within the convex hull of the zeros of Q(z) (the smallest “rubber band” shape that can enclose all these “nails”).

All the zeros of Q(z) or “nails” are either the origin or on the unit circle. This means every single zero of Q(z) is located inside or on the closed unit disk $\overline{B(0; 1)}$ which is a convex set, too.

By definition, the convex hull of a set of points is the smallest convex set containing all of them. Since all our points are already inside the convex set $\overline{B(0; 1)}$, their convex hull (the “rubber band” in our metaphor) must also be contained entirely within $\overline{B(0; 1)}$.

By the Gauss-Lucas Theorem, all zeros of P(z) must lie inside the convex hull of the zeros of Q(z) and the convex hull of the zeros of $Q(z)$ lies inside the closed unit disk $\overline{B(0; 1)}$, therefore all zeros of the polynomial P(z) are located inside the closed unit disk.

Exercises

• Let G be a region. Suppose f is an analytic complex function f: $G \to \mathbb{C}$ and also suppose that f is real-valued (f(z) is real for all $z \in G$). Then, show that f is constant.

  This is a classic result that shows just how “rigid” analytic functions are (or how restrictive the condition that f(z) is analytic is). It’s impossible for the function to only output real numbers unless it’s just a constant value.

Solution

Let $z_0 \in G, f(z_0) = x \in \mathbb{R}$. Let S = {z ∈ G: f(z) = f(z₀)}.

$f(z) = u(x, y) + iv(x, y)$ is real-valued, which means its imaginary part, $v(x, y) = 0 \text{for all } (x, y) \in G$, must be zero everywhere.

For f to be analytic, its real and imaginary parts must satisfy the Cauchy-Riemann equations at every point in G: $v(x, y) = 0 \leadsto u_x = v_y = 0, u_y = -v_x = 0$. This is a powerful result: we’ve shown that our function’s real part, u(x, y), has zero partial derivatives in all directions.

G is a region (an open and connected set). We could use the following theorem from multivariable calculus.

Theorem. If $f: D \rightarrow \mathbb{R}$ is differentiable on a connected domain $D \subseteq \mathbb{R^{\mathnormal{n}}}$, and $\nabla f(x) = \mathbf{0} \text{ for all } x \in D$, then f is constant throughout D.

The gradient $\nabla f$ encodes the direction of steepest increase. If it’s zero everywhere, the function has no slope in any direction (think of it as a landscape, if every slope in every direction is zero, then the terrain must be perfectly level). If the domain were disconnected, the function could be constant on each piece but take different values on different components. Connectivity ensures there’s no “jump.”

Another alternative is as follows. Since G is a region, which means it is connected, it guarantees that we can always draw a continuous path $\gamma$ from $z_0$ to $z$ that stays entirely inside G.

The Fundamental Theorem of Line Integrals from multivariable calculus tells us how to find the total change in a differentiable scalar function u on a domain $D\subseteq \mathbb{R^{\mathnormal{n}}}$ between two points by integrating its rate of change (its gradient) along any path $\gamma$ connecting them, $u(z) - u(z_0) = \int_{\gamma} \nabla u \cdot d\vec{r}$. The theorem states that no matter which path you take between two points, the total accumulated change equals the difference in function values.

$\nabla u = (u_x, u_y), d\vec{r} = (dx, dy)$. So, $\nabla u \cdot d\vec{r} = u_x dx + u_y dy$.

Therefore, $u(z) - u(z_0) = \int_{\gamma} \nabla u \cdot d\vec{r} = \int_{\gamma} (u_x dx + u_y dy) =[\text{As we have previously stated, } u_x = 0, u_y = 0] \int_{\gamma} (0 \cdot dx + 0 \cdot dy) = 0 \leadsto u(z) = u(z_0)$.

Since $z_0$ was fixed and z was any other (arbitrary) point in G, we have successfully shown that the value of u, and therefore f, is the same (constant) everywhere in the domain.

• Find all complex numbers z∈C for which cos(z) is real.

Solution

Express cos(z) in terms of x and y using the exponential definition:

$$ \begin{aligned} cos(z) &=\frac{e^{iz}+e^{-iz}}{2} \\[2pt] &\text{Substitute z = x + iy:} \\[2pt] &=\frac{e^{i(x+iy)}+e^{-i(x+iy)}}{2} = \frac{e^{ix-y}+e^{-ix+y}}{2} = \frac{e^{-y}e^{ix}+e^{-ix}e^y}{2} \\[2pt] &\text{Apply Euler's formula, } e^{ix} = cos(x)+isin(x)\\[2pt] &=\frac{e^{-y}(cos(x)+isin(x))+(cos(x)-isin(x))e^y}{2}. \end{aligned} $$

Now we group the terms with i (the imaginary part) and the terms without i (the real part).

$$\begin{aligned} \cos(z) &= \frac{1}{2} \left[ \underbrace{e^{-y}\cos(x) + e^y\cos(x)}_{\text{Real Part}} + i \cdot \underbrace{(e^{-y}\sin(x) - e^y\sin(x))}_{\text{Imaginary Part}} \right] \\[10pt] &= \underbrace{\cos(x) \left(\frac{e^y + e^{-y}}{2}\right)}_{\text{Real Part}} + i \cdot \underbrace{\sin(x) \left(\frac{e^{-y} - e^y}{2}\right)}_{\text{Imaginary Part}} \end{aligned}$$

$\cos(z) = \cos(x)\cosh(y) - i\sin(x)\sinh(y)$ where $\cosh$ and $\sinh$ are hyperbolic functions.

For $\cos(z)$ to be real, the imaginary part must be zero: $\text{Im}(\cos(z)) = -\sin(x)\sinh(y) = 0$

Since the product of two terms is zero, at least one of the terms must be zero:

1. sin(x) = 0 ⇔ x = nπ, n∈ℤ. Any point on the vertical lines $x=\dots, -\pi, 0, \pi, 2\pi, \dots$ in the complex plane.
2. $\sinh(y) = 0 \iff e^y = e^{-y} \iff e^{2y} = 1 \iff 2y = 0 \iff y = 0$, which is the real axis in the complex plane.

This means $\cos(z)$ is real if and only if $z$ lies on the real axis OR $z$ lies on one of the vertical lines $x = n\pi$.