Fundamental Theorem of Calculus for Contours

The computer was born to solve problems that did not exist before, Anonymous

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

• A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
• Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
• Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
• Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

Fundamental Theorem of Calculus for Contours

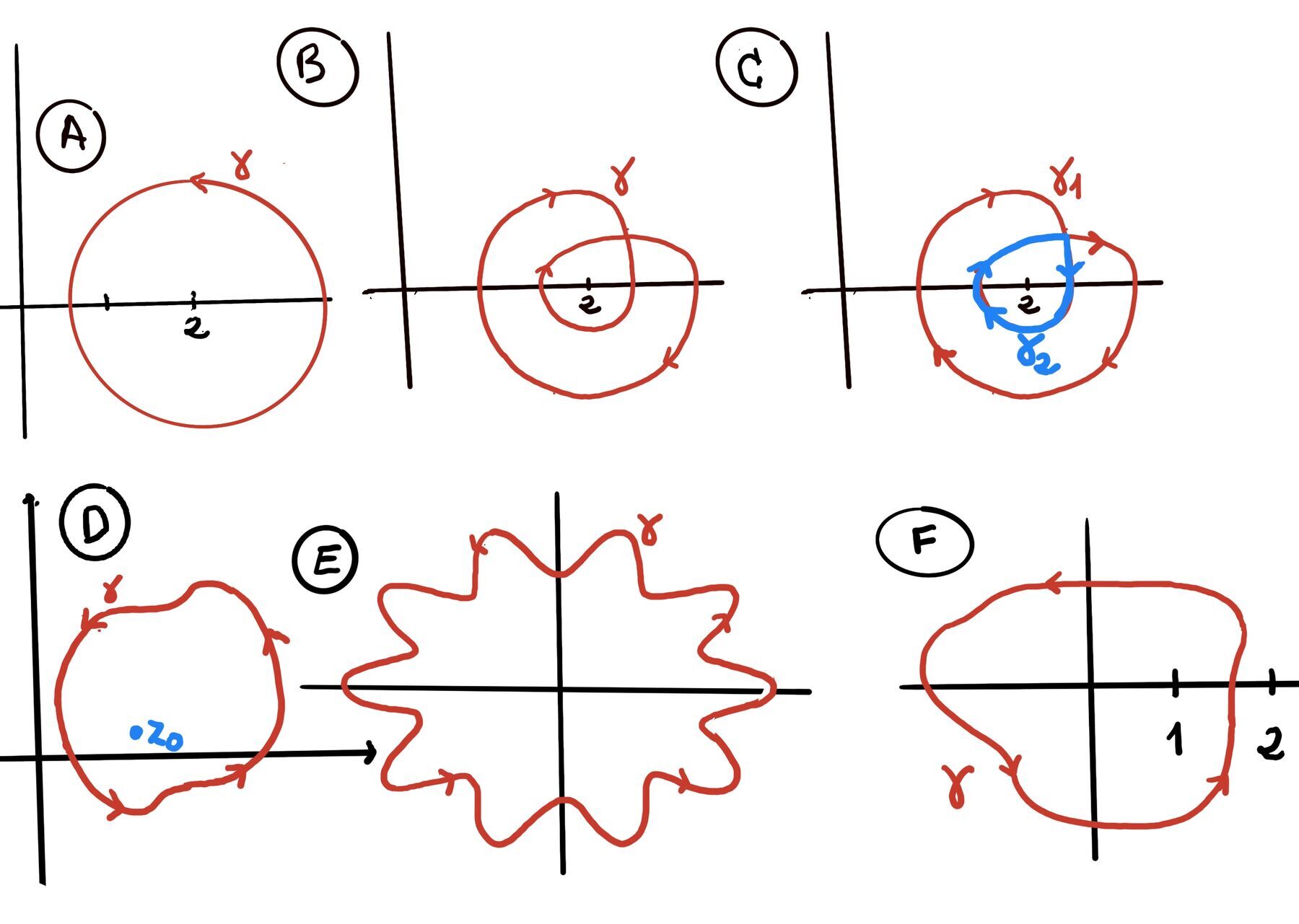
The Fundamental Theorem of Calculus in complex analysis extends the classical real-variable theorem to contour integrals in the complex plane. It provides a method to evaluate integrals over paths in the complex domain using antiderivatives, simplifying calculations and linking complex differentiation and integration.

Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

This result mirrors the real case $\int_a^b f(x)dx = F(b)-F(a)$, but generalized to curves in the complex plane. The crucial requirements are:

1. Analyticity (consequence): If a function f(z) has an antiderivative in a domain D, it is a proven fact that f(z) must be analytic in D.
2. Existence of Antiderivative: This is the only direct requirement for the theorem to hold is the existence of an antiderivative F(z) in a domain D containing the path or contour.
3. Simply Connected Domain (A Sufficient, Not Necessary, Condition). A simply connected domain (“no holes”) is a powerful condition that guarantees an antiderivative exists for every analytic function within it. However, if you can find an antiderivative by other means, the theorem works perfectly fine on domains with holes.

   These guarantee that the integral of the derivative collapses neatly to the difference in endpoint values. In other words, it establishes path independence. When a function has an antiderivative, the value of its integral between two points depends only on the endpoints, not the specific contour or path taken between them.

Proof

Parameterize the contour: $z=\gamma(t)$ with $t \in [a,b]$. Then, $\int_\gamma f(z)dz = \int_a^b F'(\gamma(t))\gamma'(t)dt$.

Assume that $\gamma$ is smooth, then $F \circ \gamma$ is differentiable. By the chain rule, $\frac{d}{dt}[F(\gamma(t))] = F'(\gamma(t))\gamma'(t)$. Thus:

$\int_a^b F'(\gamma(t))\gamma'(t)dt = \int_a^b \frac{d}{dt}[F(\gamma(t))]dt = \int_a^b Re(\frac{d}{dt}[F(\gamma(t))])dt + i\cdot \int_a^b Im(\frac{d}{dt}[F(\gamma(t))])dt$

By the fundamental theorem of calculus for real integrals:

$Re(F(\gamma(t)))\Big|_a^b + i\cdot Im(F(\gamma(t)))\Big|_a^b = F(\gamma(t))\Big|_a^b = F(\gamma(b)) - F(\gamma(a))$

• Note 1. This proof applies the real-variable FTC to the real and imaginary parts of the function. However, a more direct route exists because the Fundamental Theorem of Calculus also applies to complex-valued functions of a real variable.

$\int_a^b \frac{d}{dt}[F(\gamma(t))]dt = F(\gamma(t))\Big|_a^b = F(\gamma(b)) - F(\gamma(a))$

• Note 2. If $\gamma$ is a piecewise smooth contour, then $\int_\gamma f(z)dz = \sum_{k=0}^{n-1} \int_{t_k}^{t_{k+1}} F'(\gamma(t))\gamma'(t)dt$ where $\gamma\Big|_{[t_k, t_{k+1}]}$ is smooth. Next, apply previous reasoning to $\int_{t_k}^{t_{k+1}} F'(\gamma(t))\gamma'(t)dt$ for k = 0 ··· n - 1.

Examples

• Straight line path. Consider the function $f(z) = z^2$, which is analytic everywhere in the complex plane. Let $\gamma(t)=t$, $t\in[0,1]$ be a straight line from a = 0 to b = 1. Since f is entire, it has an antiderivative on ℂ. The antiderivative of f(z) is: $F(z) = \frac{z^3}{3}.$

By the Fundamental Theorem: $\int_\gamma z^2 dz = F(1) - F(0) = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3}.$

• Path independence insight. Consider the function $f(z) = 2z$, which is analytic everywhere in the complex plane (i.e., entire). Define two paths from 0 to 1 + i. Path 1: $\gamma_1(t) = t + it, t \in [0,1]$ be a straight diagonal line. Path 2: A piecewise path consisting of: $\gamma_2(t) = t, t\in[0,1]$ (along the real axis from 0 to 1) followed by $\gamma_3(t) = 1+it, t\in[0,1]$ (vertical line from 1 to 1 + i). Since f is entire, it has an antiderivative on ℂ. The antiderivative of f(z) is: $F(z) = z^2.$

By the Fundamental Theorem of Calculus for Contour Integrals: $\int_{\gamma_1} 2z dz = F(1+i) - F(0) = (1+i)^2 - 0^2 = 1+2i-1 = 2i.$

$\int_{\gamma_2*\gamma_3} 2z dz = F(1+i) - F(0) = 2i.$

$\int_{\gamma_1} 2z dz = \int_{\gamma_2*\gamma_3} 2z dz = 2i$. The difference between these two paths forms a closed contour. Since f is analytic, Cauchy’s theorem implies the integral over this closed contour is zero, so the two integrals (contour integrals are linear) must be equal. This demonstrates path independence, a consequence of Cauchy’s theorem.

Define the closed contour $\Gamma = \gamma_1 - (\gamma_2 * \gamma_3)$, i.e., traverse $\gamma_1$ from 0 to 1 + i, then traverse $\gamma_2 * \gamma_3$ in reverse from 1 + i back to 0. Since f(z) = 2z is entire (analytic everywhere), Cauchy’s Integral Theorem gives: $\int_\Gamma f(z) dz = 0.$

By linearity of contour integrals: $\int_\Gamma f(z) dz = \int_{\gamma_1} f(z) dz - \int_{\gamma_2 * \gamma_3} f(z) dz = 0$. Hence, $\int_{\gamma_1} f(z) dz = \int_{\gamma_2 * \gamma_3} f(z) dz$.

• Integrating an Exponential Function. Consider $f(z) = e^z$, which is entire (analytic on all of ℂ). Let $\gamma(t)=e^{it}, t\in[0,2\pi]$ be a circular contour (closed loop) of radius 1 centered at the origin (unit circle). Since f is entire, it has an antiderivative on ℂ. Indeed, $F(z) = e^z$ satisfies $F'(z) = e^z = f(z)$. By de Fundamental Theorem of Calculus for Contour Integrals, $\int_\gamma f(z)dz = \int_\gamma e^zdz = F(\gamma(2\pi)) - F(\gamma(0))$. But $\gamma(2\pi)=\gamma(0)=1$, so the difference vanishes F(1) − F(1) = 0. Hence: $\int_\gamma e^zdz = 0$. This result is also consistent with Cauchy’s Integral Theorem, which states that the integral of an analytic function over a closed contour is zero.

• Closed contour case. Consider $f(z) = cos(z)$, which is entire (analytic on all of ℂ). Let $\gamma(t)=e^{it}, t\in[0,2\pi]$ be a circular contour (closed loop) of radius 1 centered at the origin (unit circle). Since f is entire, it has an antiderivative on ℂ. Indeed, $F(z) = sin(z)$ satisfies $F'(z) = cos(z) = f(z)$. By de Fundamental Theorem of Calculus for Contour Integrals, $\int_\gamma f(z)dz = \int_\gamma cos(z)dz = F(\gamma(2\pi)) - F(\gamma(0))$. But $\gamma(2\pi)=\gamma(0)=1$, so the difference vanishes F(1) − F(1) = 0. Hence: $\int_\gamma cos(z)dz = 0$. This result is also consistent with Cauchy’s Integral Theorem, which states that the integral of an analytic function over a closed contour is zero.

• Nonlinear path. Consider $f(z) = \frac{1}{z}$. It is analytic on ℂ∖{0}. Its admits an antiderivative $F(z)=\log(z)$ but the complex logarithm is multi-valued. To make it single-valued, we choose a branch cut — across that ray the chosen branch of arg is discontinuous.

Here, we define: F(z) = log(z) = ln∣z∣ + iarg(z), with $arg(z) \in (-\frac{\pi}{2}, \frac{3\pi}{2}]$. This choice places the branch cut along the negative imaginary axis, i.e., the set {z ∈ ℂ: Re(z) = 0, Im(z) < 0}. The function is defined and single-valued on $\mathbb{C}$ minus the negative imaginary axis.

If a point approaches the cut from the right (quadrant IV side) the argument approaches $\tfrac{3\pi}{2}$; approaching from the left (quadrant III side) it approaches $-\tfrac{\pi}{2}$. The jump in argument is $\tfrac{3\pi}{2} -\bigl(-\tfrac{\pi}{2}\bigr)=2\pi$, so the logarithm has a jump of $2\pi i$ across the cut.

On this branch, F(z) is analytic on ℂ ∖ {negative imaginary axis} and satisfies $F'(z) = f(z) = \frac{1}{z}$. Consider the contour $\gamma(t)=e^{it}$, $t\in[0,\pi]$ which traces the upper semicircle from z = 1 to z = −1.

At t = 0: γ(0) = 1, arg(1) = 0. At t = π: γ(π) = 1, arg(π) = 1.The arguments along γ range from 0 to π, which lies entirely within the interval $(-\frac{\pi}{2}, \frac{3\pi}{2}]$. Therefore, the contour γ does not cross the branch cut along the negative imaginary axis.

Since F(z) is analytic on a domain containing γ, we can apply the Fundamental Theorem for Contour Integrals:

$\int_\gamma \frac{1}{z}dz = F(-1)-F(1)$.

Using our chosen branch: F(−1) = ln∣−1∣ + iarg(−1) = 0+ iπ = iπ, F(1) = ln∣1∣ +iarg(1) = 0 + i(0) = 0.

$\int_\gamma \frac{1}{z}dz = F(-1)-F(1) =iπ − 0 = iπ$.

• Consider the function $f(z) = 3z^2$, which is analytic everywhere in the complex plane. Compute $\int_{\gamma} 3z^2dz$. The contour is given by $\gamma(t) = 2t + i$, $t \in [0,1]$. This is a straight line segment from $\gamma(0) = i$ to $\gamma(1) = 2 + i$.

An antiderivative F(z) such that F′(z) = f(z) is $F(z) = z^3$.

Since $f(z) = 3z^2$ is analytic everywhere and $F(z) = z^3$ is an antiderivative, the fundamental theorem for contour integrals gives: $\int_{\gamma} 3z^2dz = F(\gamma(1)) - F(\gamma(0))$.

(2+i)² = 4 + 4i + i² = 4 + 4i −1 = 3 + 4i, (2 + i)³ =(2 + i)(3 + 4i) = 6 + 8i + 3i + 4i² = 6 + 11i −4 = 2 + 11i.

Substitute the endpoints: $F(\gamma(0)) = (i)^3 = -i, F(\gamma(1)) = (2+i)^3 = 8 + 12i - 6 - i = 2 + 11i$.

Therefore: $\int_{\gamma} 3z^2dz = (2 + 11i) - (-i) = 2 + 12i.$

• Consider the function $f(z) = e^z$. An antiderivative F(z) such that F′(z) = f(z) is $F(z)=e^z$. The contour is given by $\gamma(t) = t e^{i\pi/4}, t \in [0,2]$. Evaluate $\int_\gamma e^zdz$.

The contour is a straight line segment from a straight line from γ(0) = 0 to γ(2) = $2e^{i\pi/4} =[\text{Using Euler’s formula}]2(\cos(\pi/4)+i\sin(\pi/4))=2(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2})=\sqrt{2} + i\sqrt{2}$.

Since $f(z) = e^z$ is analytic everywhere and $F(z) = e^z$ is an antiderivative, the fundamental theorem for contour integrals gives:

$\int_\gamma e^zdz = F(\gamma(2)) - F(\gamma(0))$

Substitute the endpoints: $F(γ(0))=F(0)=e^0=1, F(γ(2))= e^{\sqrt{2} + i\sqrt{2}} = e^{\sqrt{2}} \cdot e^{i\sqrt{2}} = e^{\sqrt{2}}(\cos(\sqrt{2}) + i\sin(\sqrt{2}))$

$\int_\gamma e^zdz = F(\gamma(2)) - F(\gamma(0)) = e^{\sqrt{2}}(\cos(\sqrt{2}) + i\sin(\sqrt{2})) - 1$

Final result:

$\boxed{\int_\gamma e^zdz = e^{\sqrt{2}}\big(\cos(\sqrt{2}) + i\sin(\sqrt{2})\big) - 1}$