Bounding Complex Integrals: The Estimation Theorem and ML-Inequality

You, yourself, as much as anybody in the entire universe, deserve your love and affection, Buddha

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

• A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
• Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
• Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
• Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

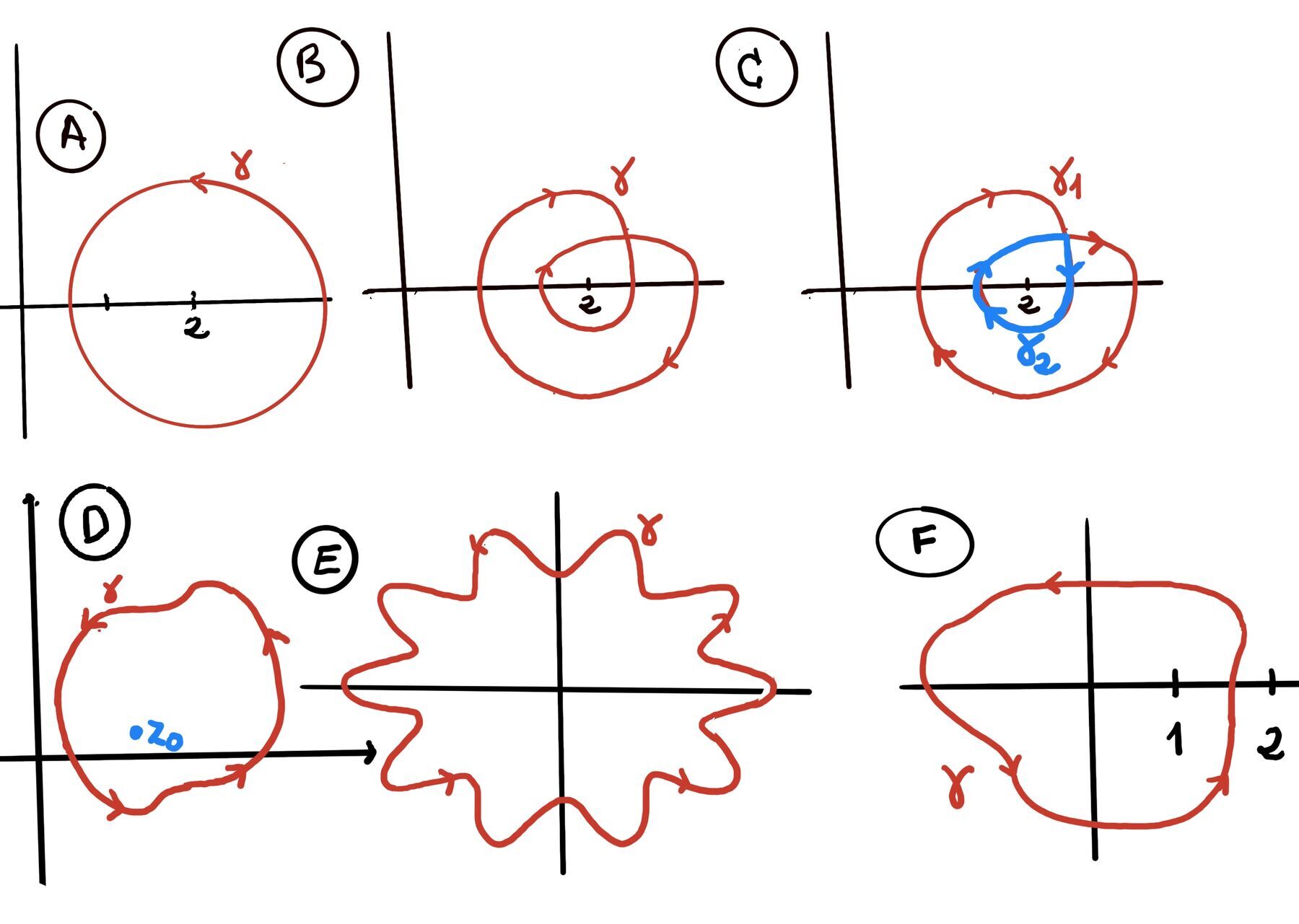
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

Estimation Theorem or the Triangle Inequality for Integrals

Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

This means the modulus (absolute value) of the integral of f over an interval does not exceed the integral of its modulus over the same interval. The inequality follows fundamentally from the triangle inequality for complex numbers and is valid for both real and complex integrals.

The integral $\int_a^b f(t)dt$ sums up tiny complex vectors, f(t)dt, from t = a to t = b. Since these vectors can point in different directions, they might partially cancel each other out. The result is the net displacement from start to finish.

The integral $\int_a^b |f(t)|dt$ sums up the lengths (magnitudes) of those same tiny vectors. Since lengths are always positive, there’s no cancellation; you are summing the total distance traveled.

The theorem simply states that your final or net displacement can never be greater than the total distance you traveled to get there.

Proof.

• Case 1. The integral is zero. If $\int_a^b f(t)dt = 0$, then its modulus is $|\int_a^b f(t)dt| = |0| = 0$.

On the right side of the inequality, the term |f(t)| is the modulus of a complex number, which is always a non-negative real number. The integral of a non-negative function, $∣\int_a^b |f(t)|dt|$, must therefore also be a non-negative real number (i.e., ≥ 0).

• Case 2. The integral is non-zero, $\int_a^b f(t)dt \ne 0$. Since the integral is just a single, non-zero complex number, we can write it in its polar form. Here, r is its magnitude (a positive real number) and θ is its angle or argument, $\int_a^b f(t)dt = re^{i\theta}$. By definition, the magnitude of $re^{i\theta}$ is r so, the left side of our theorem is simply r, r = $∣\int_a^b f(t)dt|$.

$\int_a^b f(t)dt = re^{i\theta} [\text{Multiply both sides by} e^{-i\theta}] e^{-i\theta}(\int_a^b f(t)dt) = e^{-i\theta}(re^{i\theta}) = r$. Since $e^{-i\theta}$ is a constant, we can move it inside the integral: $r = \int_a^b e^{-i\theta}f(t)dt$.

r =[Because r is a real number, it is equal to its own real part] Re(r) = $Re(\int_a^b e^{-i\theta}f(t)dt)$

$\int_a^b g(t)dt = \int_a^b Re(g(t))dt + i\int_a^b Im(g(t))dt$, a fundamental property of integrals is that the real part of an integral is the integral of the real part.

r = Re(r) = $Re(\int_a^b f(t)dte^{-i\theta}) = \int_a^b Re(e^{-i\theta}f(t))dt$ [*@]

For any complex number z, its real part can never be larger than its total magnitude, $Re(e^{-i\theta}f(t)) \le |e^{-i\theta}f(t)| =[\text{The modulus of a product is the product of the moduli}] |e^{-i\theta}||f(t)| =$ $[\text{Any point on the unit circle has magnitude 1, } |e^{-i\theta}| = 1]$ = |f(t)| [*$]

We combine the results from the previous steps: r = $∣\int_a^b f(t)dt| =[*@] \int_a^b Re(e^{-i\theta}f(t))dt \le \int_a^b |f(t)|dt$

Last Step. We know ([*$]) that the function inside this integral is always less than or equal to ∣f(t)∣. Therefore, the integral of the first function must be less than or equal to the integral of the second.

Therefore, $r = ∣\int_a^b f(t)dt| \le \int_a^b |f(t)|dt$ ∎

Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

The arc length l(γ) of a contour γ represents the total “distance traveled” along the contour in the complex plane. When we have a contour γ parameterized by γ(t) = x(t) + iy(t) for t ∈ [a, b], the arc length element |dz| (also denoted as ds) represents an infinitesimal (tiny) segment of the contour’s length corresponding to a small change dt in the parameter t. This segment can be approximated by a straight line with horizontal component dx = x’(t)dt and vertical component dy = y’(t)dt, and using the Pythagorean theorem, is: |dz| =[different notation, segments are always positive] ds = $\sqrt{dx² + dy²} = \sqrt{x'(t)²dt² + y'(t)²dt²} = \sqrt{x'(t)² + y'(t)²} dt$

Physical Interpretation: Think of γ(t) as describing the position of a particle moving in the complex plane: γ’(t) = x’(t) + iy’(t) is the complex velocity of the particle; |γ’(t)| is the speed of the particle (how fast it’s moving); |dz| = |γ’(t)| dt is the distance traveled in time dt.

Since γ’(t) = x’(t) + iy’(t), we have |γ’(t)| = $\sqrt{x'(t)² + y'(t)²}$. Therefore: |dz| = ds = |γ’(t)| dt. To get the total arc length, we sum up (integrate) all these tiny segments: $l(γ) = \int_a^b ds = \int_a^b |γ'(t)| dt = \int_a^b \sqrt{x'(t)² + y'(t)²} dt$

• Example. For a circular arc $\gamma(t) = e^(it) = cos(t) + i\cdot sin(t), t ∈ [0, \pi]: \gamma'(t) = -sin(t) + i\cdot cos(t)$

$|\gamma'(t)| = \sqrt{(-sin(t))² + cos(t)²} = \sqrt{sin²(t) + cos²(t)} = 1, |dz| = |\gamma'(t)| dt = 1 dt$

$l(γ) = \int_0^\pi |dz| = \int_0^\pi 1 dt = \pi$. This confirms that the arc length of a semicircle of radius 1 is indeed π.

• Intuitive idea. $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$. The total accumulated effect along a path (magnitude of the contour integral) cannot exceed the maximum effect per unit length (maximum function value) times the total length traveled. This is the complex analogue of the real inequality: $\left|\int_a^b f(x)dx\right| \leq (b-a) \cdot \max_{x\in[a,b]} |f(x)|$. In the complex case, $(b-a)$ is replaced by the arc length $l(\gamma)$.

• Different notation (same idea). $\int_\gamma ∣f(z)∣∣dz|$ represents the integral of |f(z)| with respect to arc length along the contour. In terms of our parameterization: $\int_\gamma |f(z)| |dz| = \int_a^b |f(\gamma(t))| |\gamma'(t)| dt$. Here, |dz| is the arc length element, which equals |γ’(t)| dt.

Given that |f(z)| ≤ M for all z on γ, we have: $\int_\gamma |f(z)| |dz| = \int_a^b |f(\gamma(t))| |\gamma'(t)| dt ≤ \int_a^b M |\gamma'(t)| dt = M \int_a^b |\gamma'(t)| dt = M·l(\gamma)$. Therefore, M·l(γ) is an upper bound for $\int_\gamma |f(z)| |dz|$

• Proof

The contour integral is defined as: $\int_\gamma f(z)dz = \int_a^b f(\gamma(t))\gamma^{'}(t)dt$. This represents summing up the function values multiplied by the “infinitesimal displacement” along the curve.

Taking absolute values and applying the triangle inequality for integrals: $∣\int_\gamma f(z)dz| = |\int_a^b f(\gamma(t))\gamma^{'}(t)dt| \le \int_a^b |f(t)|dt = \int_a^b |f(\gamma(t))||\gamma^{'}(t)|dt$ ($|zw| = |z||w|$ for complex numbers).

Since $|f(\gamma(t))| ≤ M$ for all $t \in [a,b]$:

$\int_a^b |f(\gamma(t))||\gamma^{'}(t)|dt \le \int_a^b M \cdot |\gamma^{'}(t)|dt = M \int_a^b \cdot |\gamma^{'}(t)|dt = M·l(\gamma)$

Examples

• Integral of a Complex Function over a Line Segment. Suppose we have a complex function $f(z) = z^2$ that we want to integrate over a line segment $\gamma$ from z = 0 to z = 1.

The Estimation Theorem (or ML-Inequality) states: $\left| \int_{\gamma} f(z) dz \right| \le \int_{\gamma} |f(z)| |dz|$.

Step 1. We compute the left size. The line segment from 0 to 1 can be parametrized by γ(t) = t for t∈[0, 1]. The derivative is γ′(t) = 1, so the complex differential is dz = γ′(t)dt = dt.

$\int_{\gamma} z^2dz = \int_{0}^{1} (\gamma(t))^2\gamma'(t)dt = \int_{0}^{1} t^2dt = \frac{t^3}{3}\Big|_{0}^{1} = \frac{1}{3}$. Therefore, $|\int_{\gamma} z^2dz| = |\frac{1}{3}| = \frac{1}{3}$.

Step 2. Now, we compute the integral on the right-hand side. $\int_{\gamma} |z^2||dz|$.

On our path γ(t) = t, the function’s modulus is ∣f(z)∣ = ∣z²∣ = ∣t²∣ = t² (since t ≥ 0). |dz| = ∣γ′(t)dt∣ = ∣1⋅dt∣ = dt.

$\int_{\gamma} |f(z)| |dz| = \int_{0}^{1} t^2 dt = \frac{t^3}{3}\Big|_{0}^{1} = \frac{1}{3}$

Step 3. The Final Comparison, $\frac{1}{3} \le \frac{1}{3}$. The inequality holds true.

• Integral of f(z) = z over the Unit Circle. Let $\gamma$ be the unit circle |z| = 1, parameterized as $z = e^{i\theta}, \theta \in [0, 2\pi] $.

$$ \begin{aligned} \int_\gamma z dz = \int_0^{2\pi} e^{i\theta} \cdot i e^{i\theta} d\theta &=i\int_0^{2\pi} e^{2i\theta} d\theta\\[2pt] &=i\frac{e^{2i\theta}}{2i}\Big|_{0}^{2\pi}\\[2pt] &=\frac{1}{2}(e^{4\pi i} - e^0)=\frac{1}{2}(1 - 1) = 0. \end{aligned} $$

By Cauchy’s theorem, z is analytic everywhere and the integral over a closed contour must be zero.

Therefore, the modulus is also zero: $\left| \int_\gamma z dz \right| = ∣0∣= 0$

On the path γ, the function’s modulus is ∣f(z)∣ = ∣z∣ = 1. The arc-length differential is $∣dz∣=∣ie^{i \theta}d\theta| = |i| |e^{i \theta}| d\theta = 1 \cdot 1 \cdot d\theta = d\theta$.

$\int_\gamma |z| |dz| = \int_0^{2\pi} 1 \cdot d\theta = \theta \Big|_{0}^{2\pi} = 2\pi$

The Estimation Theorem compares the modulus of the complex integral to the integral with respect to arc length, $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$. Using our corrected calculations: 0 ≤ 2π ✅

• Bounding an Integral on a Circular Path. Consider $\int_{|z|=R} \frac{e^z}{z^2+1}dz$ where $R > 1$.

The ML-Inequality states that for a contour γ and a function f(z): $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$

Find $l(\gamma)$ (The Length of the Path). The contour is a circle defined by ∣z∣ = R. The length (circumference) of a circle with radius R is given by the formula 2πR. Length of contour: $l(\gamma) = 2\pi R$

Find M (The Maximum Value of ∣f(z)∣). Let z = x + iy. The modulus of $e^z \text{ is } |e^z| = |e^{x + iy}| = |e^x|\cdot |e^{iy}|$. Since x is a real number, $|e^x| = e^x, |e^{iy}| = |cos(iy)+isin(iy)| = \sqrt{cos^2(y)+sin^2(y)} = 1 \leadsto |e^z| = e^x = e^{Re(z)}$. On a circle of radius R centered at the origin, the real part x can range from −R to R. The maximum value occurs at the rightmost point, z = R. Therefore, $|e^z| = e^{Re(z)} \le e^R$

To minimize the denominator, we use the Reverse Triangle Inequality, which states ∣z₁ +z₂∣ ≥ ∣∣z₁∣ − ∣z₂∣∣. Applying this to our denominator $|z^2+1| \geq ||z^2| - ∣1∣∣$.

For any z on our contour, we know ∣z∣ = R. Therefore, ∣z²∣ = ∣z∣² = R². We also know ∣1∣=1.

$|z^2+1| \geq ||z^2| - ∣1∣∣ = |R^2 - 1|$. Since the problem states R > 1, the term R² −1 is positive, so we can drop the outer absolute value, $|z^2+1| \geq R^2 - 1$.

So $\left|\frac{e^z}{z^2+1}\right| = \frac{|e^z|}{|z^2+1|} \leq \frac{e^R}{R^2-1} = M$.

Therefore: $\left|\int_{|z|=R} \frac{e^z}{z^2+1}dz\right| \leq M \cdot l(\gamma) = (\frac{e^R}{R^2-1}) \cdot (2\pi R) = \frac{2\pi R e^R}{R^2-1}$. This result gives us a “ceiling” on the magnitude of the integral which could be extremely useful, especially for showing that an integral approaches zero as R goes to infinity.

• Let R be a positive real number greater than 1. Let $\gamma_R$ be the contour (semicircular path) $Re^{it}, 0 \le t \le \pi$. Prove that $\lim_{R \to \infin} \int_{\gamma_R} \frac{e^{iz}}{z²}dz = 0$

The primary tool for this is the ML-Inequality (also known as the Estimation Theorem), which states: $|\int_{\gamma_R} f(z)dz| \le M \cdot L$

Step 1. Compute L, the length of the contour. The contour $\gamma_R$ is a semicircle with radius R. The circumference of a full circle is 2πR. The length of our semicircular path is half of that. L = πR

Step 2. Find M (An Upper Bound for the Function’s Magnitude).

On $\gamma_R$, we substitute the parametrization $z = Re^{it} = R(cost+isint)$ into the numerator: $|\frac{e^{iz}}{z²}| = \frac{|e^{iz}|}{z²} = \frac{|e^{i(Rcos(t)+iRsin(t))}|}{z²} = \frac{|e^{iRcos(t)-Rsin(t)}|}{z²} =[|e^{a+b}|=|e^ae^b|] \frac{|e^{iRcos(t)}||e^{-Rsin(t)}|}{z²} =$

We know that $|e^{iRcos(t)}| = 1$. For any real number ϕ, the complex number $e^{iϕ}$ lies on the unit circle, so its magnitude is always 1. Since R and cos(t) are real, their product is real.

$ = \frac{|e^{-Rsin(t)}|}{z²} =[\forall x \in \mathbb{R}, |e^x| = e^x] \frac{e^{-Rsin(t)}}{z²} \le[\text{On } \gamma_R, sin(t) \ge 0 \leadsto -Rsin(t) \le 0 \leadsto e^{-Rsin(t)} \le e^0 = 1] \frac{1}{R^2}$

The function eˣ is an increasing function. This means that its maximum value occurs at the maximum value of its exponent. For any point z on the contour $\gamma_R$, its distance from the origin is R. So, ∣z∣= R and ∣z²∣ = ∣z∣² = R².

Step 3. Apply the ML-Inequality and Take the Limit.

Using the ML-Inequality with the values we found: $|\int_{\gamma_R} \frac{e^{iz}}{z²}dz| \le M \cdot L = \frac{1}{R^2} \cdot \pi R = \frac{\pi}{R}$

Therefore, $0 \le |\int_{\gamma_R} \frac{e^{iz}}{z²}dz| \le \frac{\pi}{R}$. By the Squeeze Theorem, as R→∞, the term $\frac{\pi}{R}$ goes to 0. Since the magnitude of our integral is squeezed between 0 and a value approaching 0, its limit must also be 0. $\lim_{R \to \infin} |\int_{\gamma_R} \frac{e^{iz}}{z²}dz| = 0$

If the limit of the magnitude of a complex quantity is 0, the limit of the quantity itself must be 0: $\lim_{R \to \infin} \int_{\gamma_R} \frac{e^{iz}}{z²}dz = 0$ c.q.d.