Properties of Contour Integrals: Linearity, Path Manipulation, and Deformation

Silence is a source of great strength, Lao Tzu

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

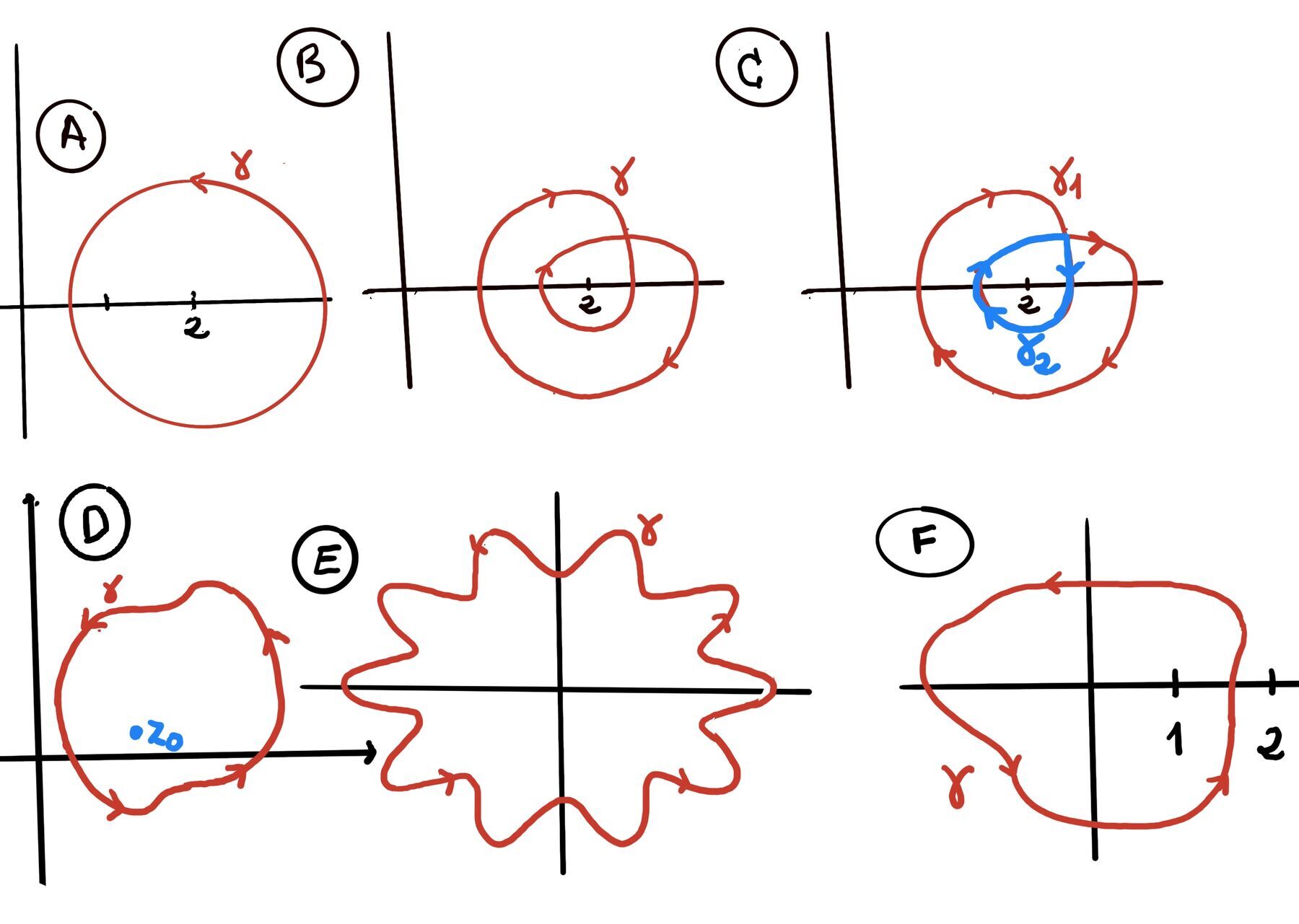
A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

• A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
• Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
• Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
• Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

The formula can be used to calculate integrals: $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

Think of integrating an analytic function around a closed loop as a “free trip”—you always end up back where you started with a net result of zero.

However, if your function has singularities (points where it “blows up,” like poles), your path is no longer free. The Residue Theorem says that for every singularity you circle, you must “pay a toll.” The residue is the exact value of that toll. The total value of the integral is simply 2πi times the sum of all the “tolls” for the singularities you enclosed on your trip.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Compute $\oint_\gamma \frac{z-1}{z(z-2)}dz$ where $\gamma$ is the circle |z| = 3. The function has singularities where the denominator is zero, namely $z_1 = 0, z_2 = 0$. Both are simple poles (order 1) inside the contour (∣0∣ < 3, ∣2∣ < 3 respectively).

Calculate the Residues: $Res(f,0) = \lim_{z \to 0}(z - 0)\frac{z-1}{z(z-2)} ​= \lim_{z \to 0} \frac{z-1}{z-2} = \frac{-1}{-2}= \frac{1}{2}.$

$​Res(f,2) = \lim_{z \to 2}(z - 2)\frac{z-1}{z(z-2)} ​= \lim_{z \to 2} \frac{z-1}{z} = \frac{1}{2}.$

$\oint_\gamma \frac{z-1}{z(z-2)}dz =[\text{Residue Theorem}] 2\pi i \sum Res(f, z_k) = 2\pi i[\frac{1}{2}+\frac{1}{2}] = 2\pi i$.

Proposition. Linearity of the contour integral. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f and g be continuous complex functions $f, g: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then, the contour integral satisfies the following linearity properties:

1. Additivity of integrands. $\int_{\gamma} (f(z) \plusmn g(z))dz = \int_{\gamma} f(z)dz \plusmn \int_{\gamma} g(z)dz$.
2. Homogeneity (scaling). $\int_{\gamma} af(z)dz = a\int_{\gamma} f(z)dz$ for any a ∈ ℂ.
3. In other words, linearity, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$

Proof:

Proof of Additivity. Consider the integral of the sum or difference of f and g:

$\int_\gamma \big(f(z)\pm g(z)\big)dz=\int_a^b \big(f(\gamma(t))\pm g(\gamma(t))\big) \gamma'(t) dt$

By the linearity of the ordinary complex integral (which follows from the linearity of ordinary real integrals for real and imaginary parts), we can distribute the integral:

$=\int_a^b f(\gamma(t))\,\gamma'(t)dt \pm \int_a^b g(\gamma(t)) \gamma'(t) d$$

Recognizing these as contour integrals of f and g respectively:

$=\int_\gamma f(z)\,dz \;\pm\; \int_\gamma g(z)\,dz.$

Proof of Homogeneity. Now consider the integral of a scalar multiple of f:

$\int_\gamma a\,f(z) dz = \int_a^b \big(a\,f(\gamma(t))\big) \gamma'(t) dt$

Since a is a constant, we can factor it out of the integral (again, by the linearity of the ordinary complex integral):

$=a\int_a^b f(\gamma(t))\gamma'(t)dt$

This is exactly a times the contour integral of f:

$=a\int_\gamma f(z) dz.$

Key insights:

1. Inheritance of Properties: The linearity of contour integrals directly inherits from the linearity of ordinary complex integrals, which in turn inherits from the linearity of Riemann integration for real-valued functions.
2. Practical Significance. These properties are fundamental for breaking down complex integrals into simpler components, factoring out constants to simplify computations, and establishing further theoretical results in complex analysis.
3. Geometric Interpretation. Linearity reflects the intuitive notion that integrating a sum of functions should equal the sum of their integrals, and scaling a function scales its integral proportionally.

Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

This proposition establishes that contour integrals are invariant under orientation-preserving reparameterizations of the contour. The key conditions are: (i) $\tilde{\gamma}$ is a reparameterization of γ via ψ; (ii) ψ has a positive continuous derivative (ensuring ψ is strictly increasing and differentiable). The positive derivative condition is crucial as it guarantees: (1) ψ is a bijection between [c, d] and [a, b]; (2) The substitution in the proof is valid; (3) The orientation of the contour is preserved.

The integral depends only on the geometric path taken and its orientation, not on how it’s parameterized. Reversing the orientation will multiply the result by -1, but any other smooth reparameterization that preserves the orientation leaves the integral unchanged. This property allows flexibility in choosing parameterizations for contour integrals and mirrors the substitution rule for definite integrals in real analysis, where the integral remains invariant under appropriate substitutions. However, while reversing orientation changes the sign of the integral, reparameterization with a positive derivative preserves both the value and the orientation.

Proof.

1. Reversal of orientation

The reversed contour $-\gamma$ is defined by $(-\gamma)(t) = \gamma(a + b - t)$ which traverses $\gamma$ backward.

The contour integral along $-\gamma$ is: $\int_{-\gamma} f(z) dz = \int_a^b f((-\gamma)(t)) \cdot (-\gamma)'(t) dt$

First, compute the derivative of $-\gamma$: $(-\gamma)'(t) = \frac{d}{dt} [\gamma(a + b - t)] =[\text{By the chain rule}] \gamma'(a + b - t) \cdot (-1) = -\gamma'(a + b - t)$

Substitute into the integral: $\int_{-\gamma} f(z) dz = \int_a^b f(\gamma(a + b - t)) \cdot \left(-\gamma'(a + b - t)\right) dt = -\int_a^b f(\gamma(a + b - t)) \gamma'(a + b - t) dt$

Now make a change of variables. Let $u = a + b - t$. Then: $du = -dt$. When $t = a, u = b$. When $t = b$, $u = a$

The integral becomes: $-\int_a^b f(\gamma(a + b - t)) \gamma'(a + b - t) dt = -\int_b^a f(\gamma(u)) \gamma'(u) (-du) = \int_b^a f(\gamma(u)) \gamma'(u) du$
Reversing the limits: $= -\int_a^b f(\gamma(u)) \gamma'(u) du$

Recognize that this is the negative of the contour integral along γ:$= -\int_{\gamma} f(z) dz$

Thus, we have shown: $\boxed{\int_{-\gamma} f(z) dz = -\int_{\gamma} f(z) dz}$ as required.

Examples:

• If $\gamma$ is the line between 0 and 1 along the real axis (it can be parametrized by $\gamma(t) = 0 + t\cdot (1-0) = t, 0 \le t \le 1, \gamma'(t) = 1$), then $-\gamma$ is the line between 1 and 0 (it can be parametrized by $-\gamma(t) = 1 + t\cdot (0-1) = 1 - t, 0 \le t \le 1, -\gamma'(t) = -1$). For the analytic function f(z)=z we compute the line integral directly, $\int_{-\gamma} zdz =[\text{Reversing the Contour/orientation}] -\int_{\gamma} zdz = -\int_0^1 tdt = -\frac{t^2}{2}\Big|_{0}^{1} = -\frac{1}{2}$

• Let $\gamma$ be the quarter-circle arc from 1 to i along the first quadrant of the unit circle (it can be parametrized by $\gamma(t)=e^{it}$ for $0 \le t \le \pi/2$), then $-\gamma$ is the same quarter-circle arc from i back to 1 (it can be parametrized by $-\gamma(t) = e^{i(\pi/2 - t)}$ for $0 \le t \le \pi/2$).

For the analytic function f(z)=z we compute the line integral directly, $\int_{-\gamma} zdz =[\text{Reversing the Contour/orientation}] -\int_{\gamma} zdz = -\int_0^{\frac{\pi}{2}} e^{it}ie^{it}dt = -i\int_0^{\frac{\pi}{2}} e^{2it}dt = -i\left[ \tfrac{e^{2it}}{2i} \right]_0^{\pi/2} = -\tfrac{1}{2}\left(e^{i\pi} - e^{0}\right) = -\tfrac{1}{2}\left(-1 - 1\right) = 1.$

Direct Computation on $-\gamma$.

$\int_{-\gamma} zdz = \int_0^{\frac{\pi}{2}} e^{i(\pi/2 - t)}\cdot (-ie^{i(\pi/2 - t)})dt = -i\int_0^{\frac{\pi}{2}} e^{2i(\pi/2 - t)}dt = -i\int_0^{\frac{\pi}{2}} e^{i\pi}e^{-2it}dt[e^{\pi i} = -1] =$

$= i\int_0^{\frac{\pi}{2}}e^{-2it}dt = \left[ \tfrac{e^{-2it}}{-2} \right]_0^{\frac{\pi}{2}} = \frac{1}{2}-\frac{-1}{2} = 1.$

2. Additivity under Subdivision

Let c be a point such that a < c < b. Define: $\gamma_1 = \gamma|_{[a, \gamma_1]}$ (the restriction of γ to [a, c]) and $\gamma_2 = \gamma|_{[c, b]}$ (the restriction of γ to [c, b]).

The contour integral along γ is: $\int_{\gamma} f(z) dz = \int_a^b f((\gamma)(t)) \cdot (\gamma)'(t) dt$

By the additive property of definite integrals (for real integrals) $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx$, we can split the integral at t = c:

$ \int_a^b f((\gamma)(t)) \cdot (\gamma)'(t) dt = \int_a^c f((\gamma)(t)) \cdot (\gamma)'(t) dt + \int_c^b f((\gamma)(t)) \cdot (\gamma)'(t) dt$

The first and second integrals are exactly the contour integral on the subpaths γ₁ and γ₂ respectively. Therefore, $\int_{\gamma} f(z) dz = \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz$ which is exactly the stated property.

• Example 1. Compute $\int_{\gamma} f(z)$ where f(z) = $\bar{z}$ and $\gamma$ is a path that can be divided into two separate paths, $\gamma_1$ a line between 0 to 1 along the real axis (it can be parametrized by $\gamma_1(t) = 0 + t·(1-0) = t, 0 \le t \le 1, \gamma_1^{'}(t)=1$) and $\gamma_2$, a second line from 1 to 2 + i (it can be parametrized by $\gamma_2(t) = 1 + t·(1+i) = (1 + t) + it, 0 \le t \le 1, \gamma_2^{'}(t)=1+i$).

$$ \begin{aligned} \int_{\gamma} f(z)dz &=\int_{\gamma_1} \bar{z}dz + \int_{\gamma_2} \bar{z}dz \\[2pt] &=\int_{0}^{1} t·1dt + \int_{0}^{1} ((1+t)-it)·(1+i)dt\\[2pt] &\text{Simplifying the integrand: } ((1+t)−it)(1+i)=(1+t)(1)+(1+t)(i)−it(1)−it(i)\\[2pt] &=1+t+i+it−it−i^2t = 1+t+i+t = 1+2t+i\\[2pt] &=\frac{t^2}{2}\Big|_{0}^{1}+[t+t^2+it]\big|_{0}^{1}\\[2pt] &=\frac{1}{2}-0 + (1 + 1^2 + i·1) - (0 + 0 + 0) = \frac{1}{2} + 2 + i = \frac{5}{2}+i. \end{aligned} $$

• Example 2. Compute $\oint_\gamma \frac{2z + 1}{z(z-1)^2}dz$ where $\gamma$ is the curve shown in Figure A (it is traversed in the 8 shape). The contour is not simple, so we break $\gamma$ into $\gamma_1$ encloses only z = 1, oriented counterclockwise (positive), and $\gamma_2$ encloses only z = 0, oriented clockwise (negative) as shown in Figure B. Both of these two new contours are simple.

$$ \begin{aligned} \oint_\gamma \frac{2z + 1}{z(z-1)^2}dz &=\oint_{\gamma_1} \frac{2z + 1}{z(z-1)^2}dz + \oint_{\gamma_2} \frac{2z + 1}{z(z-1)^2}dz \\[2pt] &=[\text{Reversing the contour, ᵞ₂ is -orientated}] \oint_{\gamma_1} \frac{2z + 1}{z(z-1)^2}dz - \oint_{-\gamma_2} \frac{2z + 1}{z(z-1)^2}dz\\[2pt] &\oint_{\gamma_1} \frac{\frac{2z + 1}{z}}{(z-1)^2}dz - \oint_{-\gamma_2} \frac{\frac{2z + 1}{(z-1)^2}}{z}dz\\[2pt] &=\text{Cauchy's Integral formula}\\[2pt] &f(z) = \frac{2z + 1}{z} = 2 + \frac{1}{z}, n = 1, z_0 = 1, f'(z) = -\frac{1}{z^2}; g(z) = \frac{2z + 1}{(z-1)^2}, z_0 = 0\\[2pt] &=\frac{2\pi i}{1!} \cdot f'(1) - 2\pi i \cdot g(0)\\[2pt] &=2\pi i \cdot -\frac{1}{1^2} - 2\pi i \cdot \frac{2\cdot 0 + 1}{(0-1)^2}\\[2pt] &=2\pi i \cdot -\frac{1}{1^2} - 2\pi i \cdot \frac{2\cdot 0 + 1}{(0-1)^2}\\[2pt] &=-2\pi i -2\pi i = -4\pi i. \end{aligned} $$

• Example 3. Compute $\oint_\gamma \frac{z}{z^2+4}dz$ where $\gamma$ is the curve shown in Figure C. The integrand has singularities at ±2i and the curve, a circle centered at 0, encloses both singularities of the integrand at z = 2i and z = −2i. The contour is not simple, f is not analytic on the interior of $\gamma$.

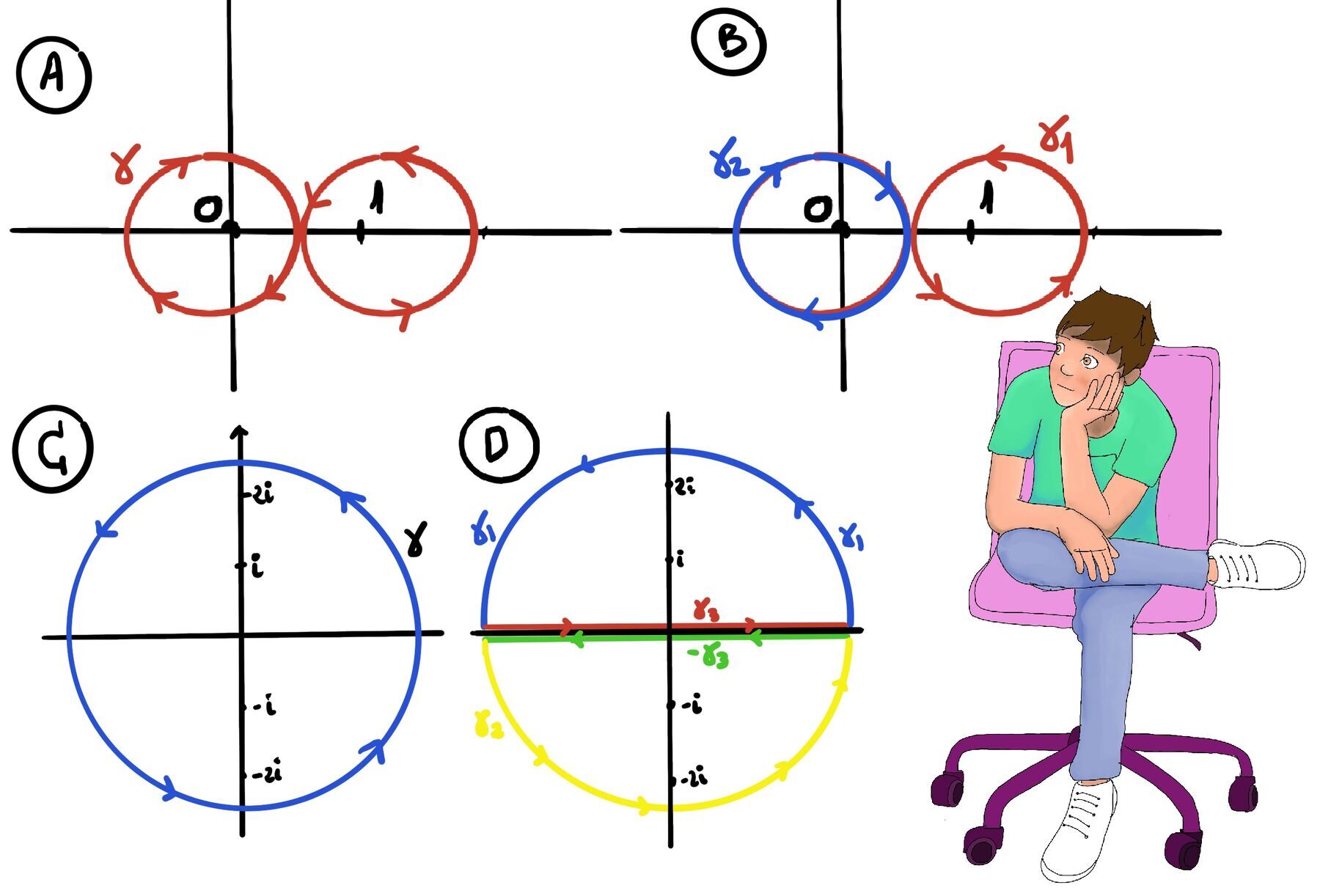
Therefore, we split the curve into two pieces (half upward/downward semicircles), where $\gamma_3$ is traversed both forward and backward, so its contributions cancel. Thus, $\gamma = \text{piece1 + piece2} = \gamma_1 + \gamma_3 -\gamma_3 + \gamma_2$ as shown in Figure D. Both of these two new pieces are simple and each surround just one singularity. Piece 1 encloses only the singularity at z = 2i and Piece 2 encloses only the singularity at z = -2i.

$$ \begin{aligned} \oint_\gamma \frac{z}{z^2+4}dz &=\oint_\gamma \frac{z}{(z-2i)(z+2i)}dz \\[2pt] &=\oint_{piece1} \oint_{piece2} \frac{\frac{z}{z+2i}}{z-2i}dz + \frac{\frac{z}{z-2i}}{z+2i}dz\\[2pt] &=\oint_{-\gamma_3 + \gamma_2} \frac{\frac{z}{z+2i}}{z-2i}dz + \oint_{\gamma_1 + \gamma_3} \frac{\frac{z}{z-2i}}{z+2i}dz\\[2pt] &=\text{Cauchy's Integral formula}\\[2pt] &=2\pi i \frac{2i}{2i+2i} + 2\pi i \frac{-2i}{-2i-2i}\\[2pt] &=2\pi i (\frac{1}{2}+\frac{1}{2})= 2\pi i. \end{aligned} $$

• Example 4. Compute $\int_{\gamma} z^2dz$ where $\gamma$ is a contour formed by joining $\gamma_1$ the line segment on the real axis from −R to R and $\gamma_1(t) = Rt, -1 \le t \le 1$ the half upper circle centered at 0 and radius R, $\gamma_2(t) = Re^{it}, 0 \le t \le \pi$.

The quickest way to solve this is by applying Cauchy’s Integral Theorem. The function being integrated is f(z) = z². As a polynomial, it is analytic (differentiable everywhere) in the entire complex plane. The path γ (a line segment joined to a semicircle) is a simple closed contour.

Cauchy’s Integral Theorem states that the integral of an analytic function over any simple closed contour is zero. Therefore, we can immediately conclude: $\int_{\gamma} z^2dz = 0$.

We can confirm this result by calculating the integral along the two separate paths, γ₁ and γ₂, and adding them together.

$\int_{\gamma} z^2dz = \int_{\gamma_1} z^2dz + \int_{\gamma_2} z^2dz$

$\int_{\gamma_1} z^2dz = \int_{-1}^1 (Rt)^2 \cdot R dt = R^3 \int_{-1}^1 t^2dt = R^3 \frac{t^3}{3}\Big|_{-1}^{1} = \frac{2R^3}{3}$

$\int_{\gamma_2} z^2dz = \int_{0}^{\pi} (Re^{it})^2 \cdot iRe^{it} dt = iR^3\int_{0}^{\pi} e^{3it} = iR^3 \frac{e^{3it}}{3i}\Big|_{0}^{\pi} = \frac{R^3}{3}(e^{3i\pi} - e^{0}) = \frac{R^3}{3}(-1-1) = -\frac{2R^3}{3}$

$\int_{\gamma} z^2dz = \int_{\gamma_1} z^2dz + \int_{\gamma_2} z^2dz = \frac{2R^3}{3} -\frac{2R^3}{3} = 0.$ The direct calculation confirms the result from Cauchy’s Theorem.

Key Insights

1. Reversal of Orientation: The proof relies on a change of variables that effectively reverses the parameterization. The negative sign arises from both the derivative of the reversed contour and the reversal of integration limits.
2. Additivity under Subdivision: The proof directly uses the additive property of real integrals. It allows us to break complex contours into simpler pieces for computation and it is indeed essential for defining integrals over piecewise smooth contours.
3. Geometric Interpretation:

• Reversal: Integrating “backward” along a path gives the negative result, reflecting the directional nature of complex integration.
• Subdivision: The integral over a path is the sum of integrals over its segments, analogous to how we break down real integrals.

3. Invariance of Contour Integrals Under Reparameterization

Proof of Invariance of Contour Integrals Under Reparameterization

Since $\tilde{\gamma} = \gamma \circ \psi$, we can apply the chain rule: $\tilde{\gamma}'(t) = \gamma'(\psi(t))\psi'(t)$.

By definition, the contour integral along $\tilde{\gamma}$ is:

$\int_{\tilde{\gamma}} f(z)dz = \int_{c}^{d} f(\tilde{\gamma}(t))\tilde{\gamma}'(t)dt =[\text{Substitute into the integral}] \int_{c}^{d}(f(\gamma(\psi(t))))\gamma'(\psi(t))\psi'(t)dt$

Make the substitution $\tau = \psi(t). Then, d\tau = \psi'(t)dt$. When t = c, $\tau = \psi(c) = a$. when t = d, $\tau = \psi(d) = b$

Since ψ′(t) > 0 for all t ∈ [c, d], the function ψ is strictly increasing, so the substitution is valid. Therefore, the integral becomes.

$\int_{\tilde{\gamma}} f(z)dz = \int_{a}^{b}(f(\gamma(\tau)))\gamma'(\tau)d\tau = \int_{\gamma} f(z)dz$. This completes the proof.

Examples.

• Let the original curve be γ(t) = t + it for 1 ≤ t ≤ 2, which traces the line segment from 1 + i to 2 + 2i.

Define the reparameterization function $\psi : [1, \sqrt{2}] \to [1, 2], \psi(t) = t^2$ so that $\psi(1) = 1, \psi(\sqrt{2}) = 2, \psi'(t) = 2t \gt 0 ∀t \in [1, \sqrt{2}]$ (since t ≥ 1), and $\psi$ is continuous on $[1, \sqrt{2}]$

The reparameterized curve is $\tilde{\gamma} = \gamma \circ \psi$, so $\tilde{\gamma}(t) = \gamma(\psi(t)) = \gamma(t^2) = t^2 + it^2$ for $t \in [1, \sqrt{2}]$

This traces the same line segment from 1+i to 2+2i, but with a different parameterization. By the proposition, for any continuous function f defined on this line segment: $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

Let f(z) = z, which is continuous on the line segment. Compute the Integral Along γ: $\int_{\gamma} f(z)dz = \int_1^2 (t + it)(1 + i) dt = \int_1^2 (1 + i)^2\cdot t dt = [\text{Since } (1 + i)^2 = 1 + 2i + i^2 = 2i] \int_1^2 t \cdot 2i dt = $

$2i \int_1^2 t dt = 2i \left[ \frac{t^2}{2} \right]_1^2 = 2i \cdot \frac{4 - 1}{2} = 2i \cdot \frac{3}{2} = 3i.$

Compute the Integral Along $\tilde{\gamma}$. $\int_{\tilde{\gamma}} f(z)dz = \int_1^{\sqrt{2}} (t^2 + i t^2) \cdot 2t(1 + i) dt = \int_1^{\sqrt{2}} t^2(1 + i) \cdot 2t(1 + i) dt = \int_1^{\sqrt{2}} 2t^3 (1 + i)^2 dt = [\text{Since } (1 + i)^2 = 1 + 2i + i^2 = 2i] \int_1^{\sqrt{2}} 2t^3 \cdot 2i dt.$

$= 4i \int_1^{\sqrt{2}} t^3 dt = 4i \left[ \frac{t^4}{4} \right]_1^{\sqrt{2}} = i \left[ t^4 \right]_1^{\sqrt{2}} = i \left( (\sqrt{2})^4 - 1^4 \right) = i(4 - 1) = 3i.$ Both integrals yield the same value. This confirms the invariance of contour integrals under reparameterization.

• Let the original curve be $\gamma(t) = e^{it}$ for t ∈ [0, π] which traces the upper half of the unit circle from 1 to −1.

Define the reparameterization function $\psi : [0, 2π] \to [0, π], \psi(t) = \frac{t}{2}$ so that $\psi(0) = 0, \psi(2π) = π, \psi'(t) = \frac{1}{2} \gt 0 ∀t \in [0, 2π]$ and $\psi$ is continuous on $[0, 2π]$.

The reparameterized curve is $\tilde{\gamma} = \gamma \circ \psi$, so $\tilde{\gamma}(t) = \gamma(\psi(t)) = \gamma(\frac{t}{2}) = e^{i(t/2)}$ for $t \in [0, 2\pi]$ which traces the same upper half of the unit circle.

By the proposition, for any continuous function f defined on this line segment: $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz ↭ \int_{\gamma} f(z)dz = \int_0^{2\pi} f(e^{i(t/2)}) \cdot \left(i \cdot \frac{1}{2} e^{i(t/2)}\right) dt$

Now, let f(z) = $\frac{1}{z}$, which is continuous on the curve (since the curve does not pass through z = 0). Compute the integral along $\gamma$.

$\int_\gamma f(z) dz = \int_0^\pi \frac{1}{e^{it}} \cdot i e^{it} dt = \int_0^\pi i dt = i \left[ t \right]_0^\pi = i\pi.$

Compute the integral along $\tilde{\gamma}$.

$\int_{\tilde{\gamma}} f(z) dz = \int_0^{2\pi} \frac{1}{e^{i t/2}} \cdot \frac{i}{2} e^{i t/2} dt = \int_0^{2\pi} \frac{i}{2} dt = \frac{i}{2}\left[ t \right]_0^2\pi = \frac{i}{2} \cdot 2\pi = i\pi$.

Both integrals yield the same value. This confirms the invariance of contour integrals under reparameterization.

• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

Key Idea: If a function f(z) is analytic in a region D, the integral over any closed contour in D is zero (by Cauchy’s theorem). Deforming a contour is valid only if the entire region between the original and deformed contours is free of singularities.

Examples

The integral $ \int_{\gamma} \frac{1}{z} dz$ is the same for any closed contour $\gamma$ enclosing the origin. For example, a circle |z| = 1 and an ellipse |z - 0.5| = 0.5 both give $2\pi i$.

The function f(z) = 1/z has a singularity at z = 0. For any closed contour γ that encloses the origin (with positive orientation), the integral is: $ \int_{\gamma} \frac{1}{z} dz$

• The circle $\gamma_1$: |z| = 1. This is a standard contour positively oriented (counterclockwise), enclosing the origin and avoiding the singularity. $ \int_{\gamma_1} \frac{1}{z} dz =[\text{The Residue Theorem}] 2\pi i \sum Res(f, z_k) = 2\pi i \sum Res(f, 0) = 2\pi i$

Note: For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$. In our particular case, $Res(f, z_0) = \lim_{z \to 0}(z-0)\frac{1}{z} = 1.$.

• $\gamma_2, \frac{x^2}{4}+\frac{y^2}{9}=1$ is an ellipse centered at the origin. The vertices are located at (0, ±3) and the co-vertices are at (±2, 0). Since it can be continuously deformed into the circle without crossing z = 0, the deformation principle applies: $ \int_{\gamma_2} \frac{1}{z} dz = \int_{\gamma_1} \frac{1}{z} dz = 2\pi i$ where $\gamma_1$: |z| = 1$.

Visual proof via a “bridge”

The Cauchy-Goursat theorem states that if a function f is analytic at all points inside and on a simple closed contour γ, then: $\oint_{\gamma} f(z)dz = 0$.

However, when dealing with functions that are not analytic everywhere, such as ($f(z) = \frac{1}{z}$), the principle of deformation of contours becomes essential. f(z) is analytic everywhere except at z = 0, where it has a simple pole. If a contour encloses this singularity, the integral may be nonzero. For instance, over the unit circle centered at the origin: $\oint_{\gamma_2}\frac{1}{z} = 2\pi i$.

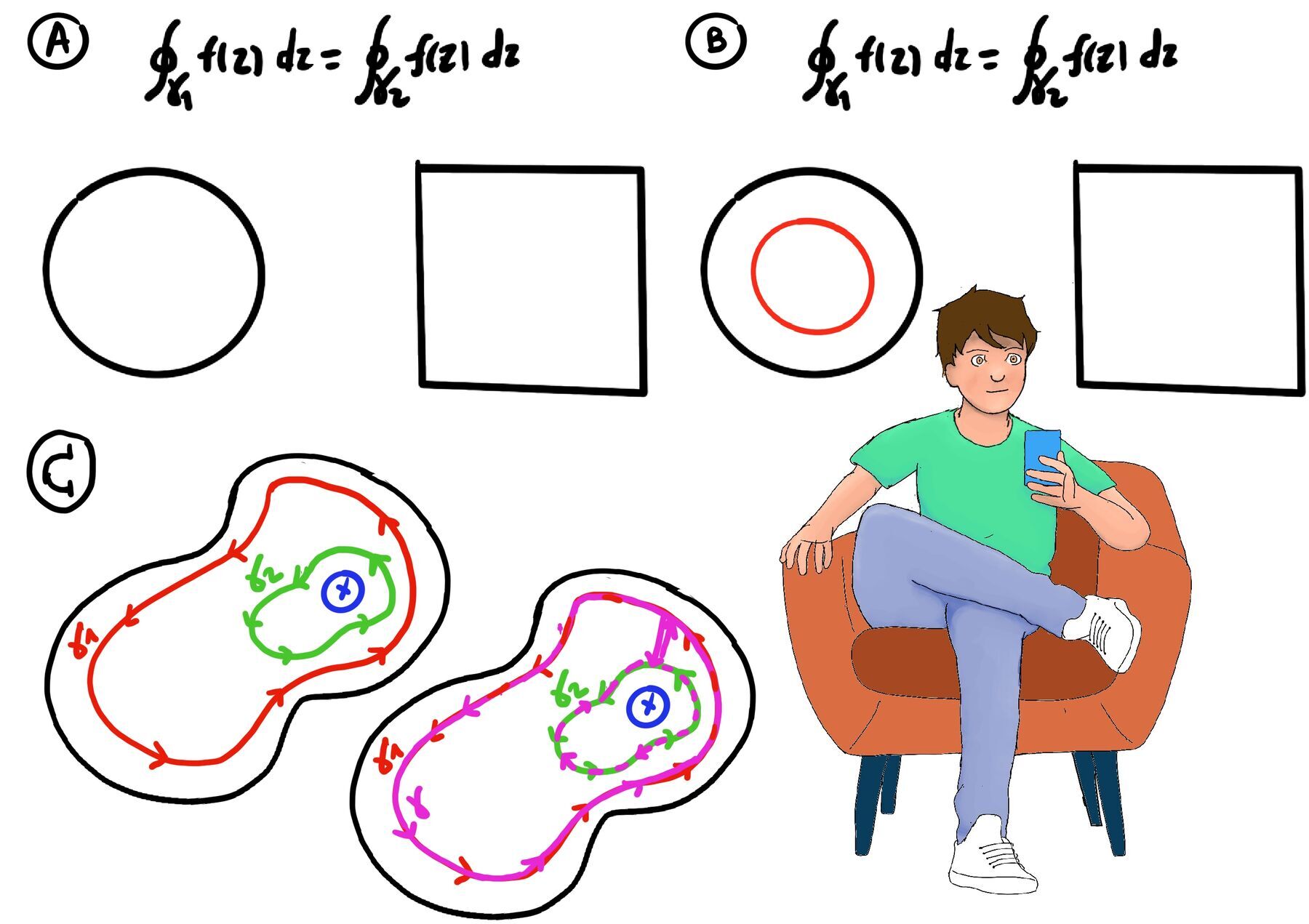
To illustrate this principle, consider two contours: ($\gamma_1$), a square centered at the origin, and ($\gamma_2$), a unit circle also centered at the origin (Figure A). While the integral of ($f(z) = \frac{1}{z}$) over the unit circle has been previously calculated as $2\pi i$, the integral over the square requires a different approach.

Using the principle of deformation of contours, one can replace ($\gamma_1$) and ($\gamma_2$) with new contours that are entirely contained within regions where the function remains analytic. For instance, if an inner circle ($\gamma_2$) with radius ($\frac{1}{2}$) is considered, the integral along this path will also yield ($2\pi i$) because the function remains analytic between the two curves (Figure B).

The theoretical foundation of the deformation principle can be visualized by constructing a new contour that connects points on ($\gamma_1$) and ($\gamma_2$). By creating a “bridge” between these contours, one can define a closed path that encircles a simply connected region:

1. Construct a New Path: We start with an outer contour γ₁ (red, counter-clockwise) and an inner contour γ₂ (green, also counter-clockwise). We create a new, single, non-intersecting closed path γ by adding a “bridge” (two lines connecting the contours).
2. Trace the Full Contour γ: The new path travels: Along γ₁ (red, counter-clockwise). Down the bridge. Along γ₂ in the opposite (clockwise) direction. Up the bridge, back to the start.
3. Apply Cauchy-Goursat: The function f(z) is analytic everywhere in the region enclosed by this new path γ (the region between the original contours). Therefore, by the Cauchy-Goursat Theorem: $\oint_{\gamma}f(z) = 0$.
4. Deconstruct the Integral: The integral over the full path γ is the sum of its parts: $\oint_{\gamma}f(z) = \oint_{\gamma_1}f(z) + \oint_{bridge}f(z) - \oint_{\gamma_2}f(z) - \oint_{bridge}f(z) = 0$. If you traverse γ₂ clockwise, pick up a minus sign.
5. Simplify and Conclude. The two bridge integrals are traversed in opposite directions, so they cancel. What remains is $\oint_{\gamma_1}f(z) - \oint_{\gamma_2}f(z) = 0 \leadsto \oint_{\gamma_1}f(z) = \oint_{\gamma_2}f(z)$

Consequently, the integral along ($\gamma_1$) equals the integral along ($\gamma_2$) (Figure C). An integral is unchanged under continuous contour deformation provided the integrand stays analytic throughout the region swept out.