The Square Root Function: From Real Numbers to Complex Analysis

Assumption is the mother of all screw-ups, Anonymous.

Introduction

The square root function is a fundamental mathematical function with wide-ranging applications in mathematics, science, and engineering. It is written as: f(x) = $\sqrt{x}$.

It gives the non-negative number that, when multiplied by itself, equal the input x. For example, $\sqrt{16}$ = 4 because 4 × 4 = 16, $\sqrt{49}$ = 47 because 7 × 7 = 49, $\sqrt{64}$ = 8 because 8 × 8 = 64.

• Domain: The domain of the square root function is the non-negative real numbers (x ≥ 0). In the realm of real numbers, you can’t take the square root of a negative number.
• Range: he set of all possible outputs is also the non-negative real numbers (y ≥ 0).
• Increasing Function: The square root function is an increasing function, meaning that as the input gets larger, the output also gets larger.
• The graph is continuous and smooth for all x ≥ 0. It starts at the origin (0, 0) and curves upward and to the right. As x approaches infinity, the function grows without bound, but the rate of growth slows down. It is a concave down curve because its second derivative is negative.
• Basic Identities: (1) Inverse Property, $(\sqrt{x})^2 = x$ for x ≥ 0; (2) Absolute Value Identity, $\sqrt{x^2} = |x|$ for x ∈ ℝ.
• Algebraic Properties: (1) Product Rule, $\sqrt{ab} = \sqrt{a}·\sqrt{b}$ for a, b ≥ 0; (2) Quotient Rule, $\sqrt{a/b} = \sqrt{a}/\sqrt{b}$ for a ≥ 0, b > 0.
• The square root function f(x) = $\sqrt{x}$ is the inverse of the square function g(x) = x², but only when the domain of g(x) is restricted to non-negative numbers (x≥0).
• The derivate of the square root function f(x) = $\sqrt{x}$ is f’(x) = $\frac{1}{2\sqrt{x}}$.
• Integral: The integral of $\sqrt{x}$ is $\frac{2}{3}x^{3/2} + C$.

Complex Square Root Function

A complex number is expressed as $ z = a + bi $, where $ a $ and $ b $ are real numbers, and $ i $ is the imaginary unit ($ i^2 = -1 $). The square root of a complex number $ z $ is a number $ w $ such that $ w^2 = z $. Unlike real numbers, every non-zero complex number has exactly two distinct square roots (and 0 has the unique root 0).

Polar-form derivation

The most straightforward method to compute complex square roots uses polar form. For any nonzero complex number z, we can write it as $z = re^{i\theta}$ where:

• r = |z| > 0 is the modulus (a positive real number, distance from the origin).
• $\theta = \arg(z)$ is the argument (angle from the positive real axis), typically taken in (-π, π] or [0, 2π).

Then the square roots are obtained by halving the modulus and the argument.

Steps to Find Square Roots:

1. Compute the modulus of the roots: $ \sqrt{r} $.
2. Compute the arguments of the roots: $ \frac{\theta}{2} $ and $ \frac{\theta}{2} + \pi $.
3. The two square roots are. $\sqrt{z} \in \\{\sqrt{r}e^{i\theta/2}, \sqrt{r}e^{i(\theta/2+\pi)}\\}$
4. Equivalently, in trigonometric form: $w_1 = \sqrt{r} \left( \cos\left(\frac{\theta}{2}\right) + i\sin\left(\frac{\theta}{2}\right) \right), w_2 = \sqrt{r} \left( \cos\left(\frac{\theta}{2} + \pi\right) + i\sin\left(\frac{\theta}{2} + \pi\right) \right) = -w_1$

For instance, the square roots of $−1=e^{\pi}$ are i = $e^{\pi/2}$ and −i = $e^{3\pi/2}$.

Why Two Roots?

Since angles in polar form are periodic ($ \theta \equiv \theta + 2\pi $), halving $ \theta $ gives two distinct roots separated by $ \pi $ radians — exactly half a full rotation — which places them on opposite sides of the origin in the complex plane.

In other words, the modulus of the root is the square root of the original modulus. The angle of the root is half the original angle. The second root lies diametrically opposite the first root (separated by $\pi$ radians).

Rectangular-form formula

If z = a + bi with z ≠ 0, assume the square roots of z to be w = u + iv, that is $\sqrt{a + bi} = u + iv$

Now, squaring both side of the equation, we have: $a + bi = u^2 -v^2 + 2iuv$. Comparing real and imaginary parts of the above equation, we have: $a = u^2 -v^2, b = 2uv$

We know that $(u^2 + v^2)^2 = (u^2 - v^2)^2 + 4u^2v^2 = a^2 + b^2 \leadsto u^2 + v^2 = \sqrt{a^2 + b^2 }$ because u² + v² is always positive as sum of squares of non-zero real numbers is always greater than zero.

Now, we have $u^2 + v^2 = \sqrt{a^2 + b^2 }$ and $a = u^2 -v^2$. Solving for these two values, we have $2u^2-a = \sqrt{a^2 + b^2} \leadsto u^2 = \frac{|z|+a}{2}, v^2 = u^2 - a = \frac{|z|+a}{2} -a = \frac{|z|-a}{2}$

Since 2uv = b, we have: (1) u and v have the same sign if b > 0 or (2) u and v have opposite signs if b < 0.

Therefore the square root of complex number a + ib (b ≠ 0) is given by $u = \sqrt{\frac{|z|+a}{2}}, v = sgn(b)\sqrt{\frac{|z|-a}{2}}, \sqrt{a + ib} = \plusmn \sqrt{\sqrt{\frac{|z|+a}{2}}+(\frac{ib}{|b|})\sqrt{\frac{|z|-a}{2}}}$

Example:

Examples

1. Square Root of 1 + i, $r = \sqrt{1^2 + 1^2} = \sqrt{2}, \theta = \arctan\left(\frac{1}{1}\right) = \frac{\pi}{4}$. Roots: $w_1 = \sqrt[4]{2} \left( \cos\left(\frac{\pi}{8}\right) + i\sin\left(\frac{\pi}{8}\right) \right), w_2 = \sqrt[4]{2} \left( \cos\left(\frac{9\pi}{8}\right) + i\sin\left(\frac{9\pi}{8}\right) \right) \text{ where } \frac{9\pi}{8} = \frac{\pi}{8} + \pi$
2. Square Root of -1, $r = 1, \theta = \pi$ Roots: $w_1 = \cos\left(\frac{\pi}{2}\right) + i\sin\left(\frac{\pi}{2}\right) = i, w_2 = \cos\left(\frac{3\pi}{2}\right) + i\sin\left(\frac{3\pi}{2}\right) = -i$
3. $\sqrt{1 + i} = \plusmn \sqrt{\sqrt{\frac{\sqrt{2}+1}{2}}+i\sqrt{\frac{\sqrt{2}-1}{2}}}$

Branches and the principal square root

Unlike real numbers, every non-zero complex number has exactly two distinct square roots. The challenge is defining a consistent function, $\sqrt{z}$, that selects one of these two values.

Now, let’s take the square root: $z^{1/2} = \sqrt{r} \cdot e^{i\theta/2}$. Recall that the argument θ is not unique. It is indeed multivalued. You can add any multiple of 2π and still represent the same complex number: $z = re^{i(\theta + 2\pi n)} \text{ for any integer } n$

So when we take the square root: $z^{1/2} = \sqrt{r} \cdot e^{i(\theta + 2\pi n)/2} = \sqrt{r} \cdot e^{i\theta/2} \cdot e^{i\pi n}$. Since $e^{i\pi n} = (-1)^n$, we get two distinct values: $\sqrt{r} \cdot e^{i\theta/2}, -\sqrt{r} \cdot e^{i\theta/2} = \sqrt{r} \cdot e^{i\theta/2+i\pi}$

A branch cut is a curve (or line) in the complex plane that we agree not to cross. Those two previous values correspond to the two branches of the square root function:

• By convention, for the square root function, the principal branch cut is the negative real axis: $f_+: \Complex \\ (-∞, 0] \to \Complex, f_+(z) = \sqrt{r} \cdot e^{i\theta/2}$ where $\theta(z) \in (-\pi, \pi], \theta(z) \in arg(z)$. Define $\boxed {\sqrt{z} = e^{\frac{1}{2}Log(z)} = \sqrt{|z|}e^{i\theta/2}}$ where $\Log(z)$ is the principal logarithm
• Secondary branch is on the same domain, $f_-: \Complex \\ (-∞, 0] \to \Complex, f_-(z) = \sqrt{r} \cdot e^{i\theta/2+i\pi}$ where $\theta(z) \in (\pi, 2\pi], \theta(z) \in arg(z)$

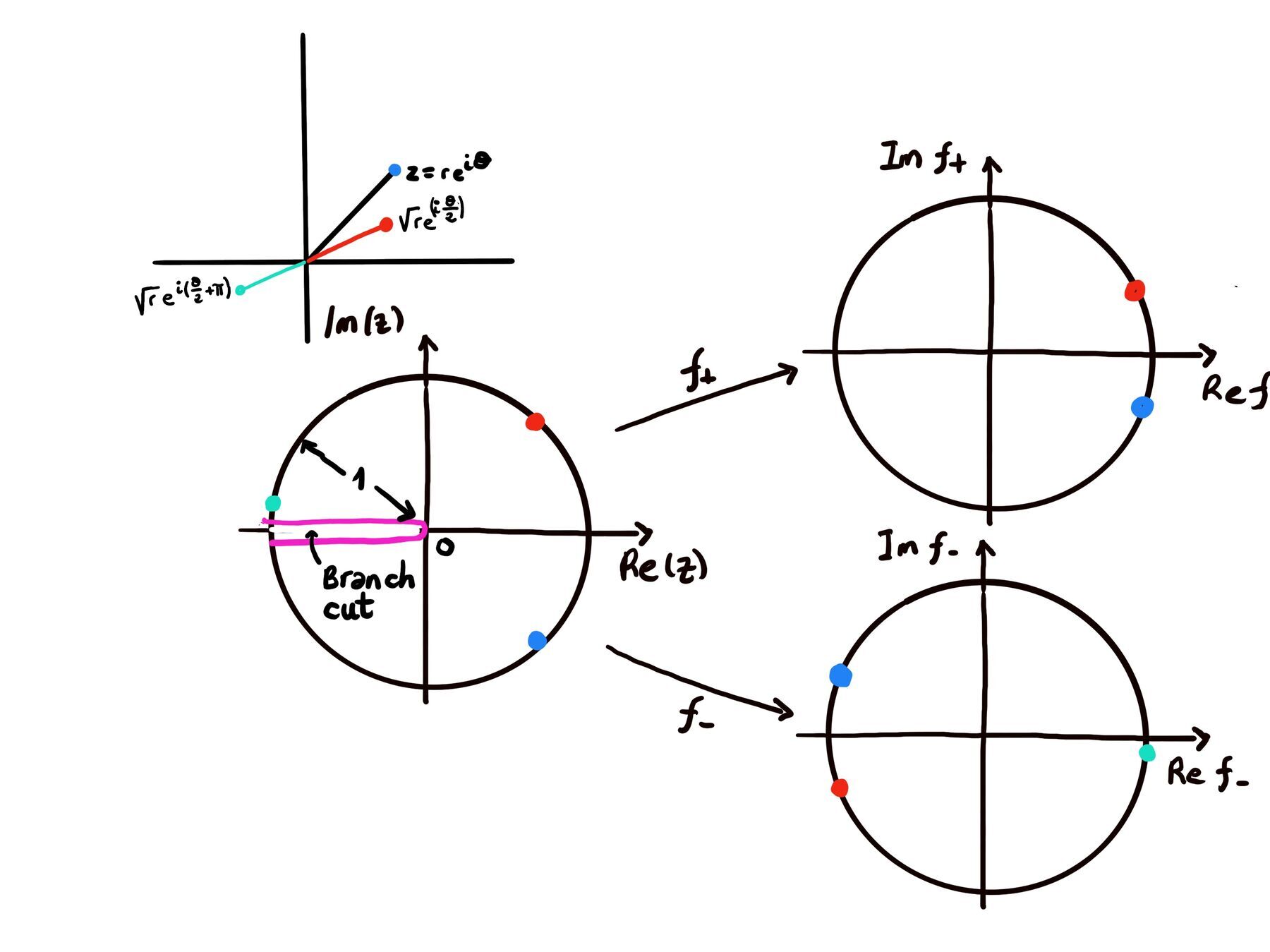
Conclusion: These branches are distinct because the square root function is not single-valued over the complex plane. To make it single-valued, we define a branch cut, typically along the negative real axis, and restrict the argument θ to a specific interval. A key feature of the principal root is that its real part is always non-negative. f⁺(z) maps the entire complex plane (minus the branch cut) to the right half-plane. Similarly, f^-(z) lies in the left half-plane, including the negative real axis.

Each branch $f^+$ or $f^-$ is holomorphic (complex-differentiable) on its domain $\mathbb{C}\setminus(-\infty,0]$. Across the cut itself, neither branch extends continuously.

Monodromy (sheet switching). Analytically continuing $\sqrt{z}$ once around a loop encircling 0 flips the sign (you move to the other sheet). Two loops bring you back.

Differentiation

For example, on the principal branch: $f_+(z)^2 = z$.

Differentiating both sides: $2·f_+(z)·f_+^{'}(z) = 1 \leadsto f_+^{'}(z) = \frac{1}{2·f_+(z)} = \frac{1}{2\sqrt{z}}$ valid on ℂ \ (-∞, 0} (and z ≠ 0).

Connection to the Complex Logarithm

A more fundamental way to define the square root is via the complex exponential and logarithm functions: $z^{1/2} = e^{\frac{1}{2}log(z)}$

The multi-valued nature of the square root comes directly from the multi-valued nature of the logarithm: log(z) = ln(r) + i(θ + 2πk).

Substituting this into the formula gives: $z^{1/2} = e^{\frac{1}{2}log(z)} = e^{\frac{1}{2} \left( \ln r + i(\theta + 2\pi k) \right)} = \sqrt{r}·e^{i\frac{\theta + 2\pi k}{2}} = \sqrt{r}·e^{i\frac{\theta}{2}}·e^{i\pi k} = \sqrt{r}·e^{i\frac{\theta}{2}}·(-1)^k$.

This shows that an even k (like k = 0, 2,…) results in one root ($e^{i\pi k} = 1$), while an odd k (like k=1,3,…) results in the other ($e^{i\pi k} = - 1$). Choosing the principal branch of the logarithm corresponds to choosing the principal branch of the square root.

Complex exponentiation

The core issue is that the complex logarithm, log(z), is a multi-valued function. For any complex number $z = re^{i\theta}$, its logarithm is log(z) = ln(r) + i(θ + 2πk) where k can be any integer (k ∈ ℤ). Each value of k produces a different value for the logarithm.

When we define $z^α := e^{α·log(z)}$. We define an analytic branch of $z^α$ by choosing a branch of Log(z), this multi-valuedness carries over: $z^α = e^{α·(ln(r) + i(θ + 2πk))} = e^{α·(ln(r) + iθ)}e^{α·i2πk}$

Let’s analyze the two parts of this product:

1. $e^{α·(ln(r) + iθ)}$: This part depends only on a single choice of θ. It forms the principal value if we choose the principal argument θ ∈ (−π, π].
2. $e^{α·i2πk}$: This is the crucial term, the multi-valued factor. It’s a multiplier that generates all the possible values of $z^α$.

The number of distinct values depends on α:

1. If α is an integer: Let α = n. The multiplier becomes $e^{i2πnk} = (e^{i2π})^{nk} = 1^{nk} = 1.$ There is only one value, as expected (z², z³, etc., are unique).
2. If α is a rational number: Let α = p/q. The multiplier is $e^{i2π·\frac{p}{q}·k}$. As $k$ varies, this term cycles through a finite set of values. It produces exactly $q$ distinct values (corresponding to $k = 0, 1, 2, ..., q-1$). This explains why there are $q$ distinct $q$-th roots ($z^{1/q}$) and, more generally, $q$ distinct values for $z^{p/q}$.
3. If α is an irrational or complex number: The multiplier $e^{i2πnk}$ produces an infinite number of distinct values, one for each integer k.

To create a proper, single-valued, and analytic (differentiable) function from $z^α$, we must make a consistent choice. By choosing a branch for log(z), we are essentially fixing the value of k (usually k = 0) and restricting the domain of the argument θ. The principal branch of zᵅ is defined by using the principal branch of the logarithm, Log(z) = ln∣z∣ + iArg(z), where Arg(z) ∈ (−π, π].

This gives the principal Value of $z^α$: $z^α = e^{α·Log(z)}$ where Arg(z) is the principal argument in (−π,π]. A key feature of the principal root is that its real part is always non-negative. It maps the entire complex plane (minus the branch cut) to the right half-plane.

Properties of the Principal Branch:

• Single-Valued: It yields one specific result for a given $z$.
• Analytic: It is a differentiable function everywhere except on its branch cut.
• Branch Cut: The function is discontinuous and non-analytic along the branch cut inherited from $\operatorname{Log}(z)$, which is the negative real axis (${z \in \mathbb{C} : \operatorname{Im}(z) = 0, \operatorname{Re}(z) \leq 0}$). This is because $\operatorname{Arg}(z)$ jumps from $π$ to $-π$ across this ray.

Example:

• $i^i = e^{i·Log(i)} =[Log(i) = ln(1) + iπ/2 = iπ/2] e^{i·(i\frac{\pi}{2})} = e^{-\frac{\pi}{2}}$ So, the principal value of $i^i$ is the real number $e^{-\frac{\pi}{2}}≈0.20788.$

The full-multivalued set is iⁱ = {$e^{-\frac{\pi}{2}}·e^{i·i2πk} = e^{-\frac{\pi}{2}-2πk} | k \in \mathbb{Z}$}

• $(-1)^i = e^{i·Log(-1)} =[Log(-1) = ln(1) + iπ = + iπ] e^{i·(i\pi)} = e^{-\pi}$ So, the principal value of $(-1)^i$ is the real number $e^{-\pi}≈0.0432.$

The full-multivalued set is (-1)ⁱ = {$e^{-\pi}·e^{i·i2πk} = e^{-(\pi + 2\pi k)} = e^{-(\pi + 2\pi k)} = e^{-(2k+1)\pi} | k \in \mathbb{Z}$}

Derivatives

• If α is a constant and a fixed branch Log, $f(z) = z^\alpha = e^{\alpha·Log(z)}, f'(z) = e^{\alpha·Log(z)}·\alpha·(Log(z))^' = z^\alpha·\alpha·\frac{1}{z} = \alpha z^{\alpha -1}$ valid on the branch domain (away from the cut and z = 0).
• If α = α(z) varies with z, $\frac{d}{dz}(z^\alpha(z)) = e^{\alpha(z)·Log(z)}·(\alpha^'(z)Log(z) + \frac{\alpha(z)}{z}) = z^\alpha(z)·(\alpha^'(z)Log(z) + \frac{\alpha(z)}{z})$.