Cauchy's Theorem for a disk

Sometimes people don’t want to hear the truth because they don’t want their illusions destroyed, Friedrich Nietzsche.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

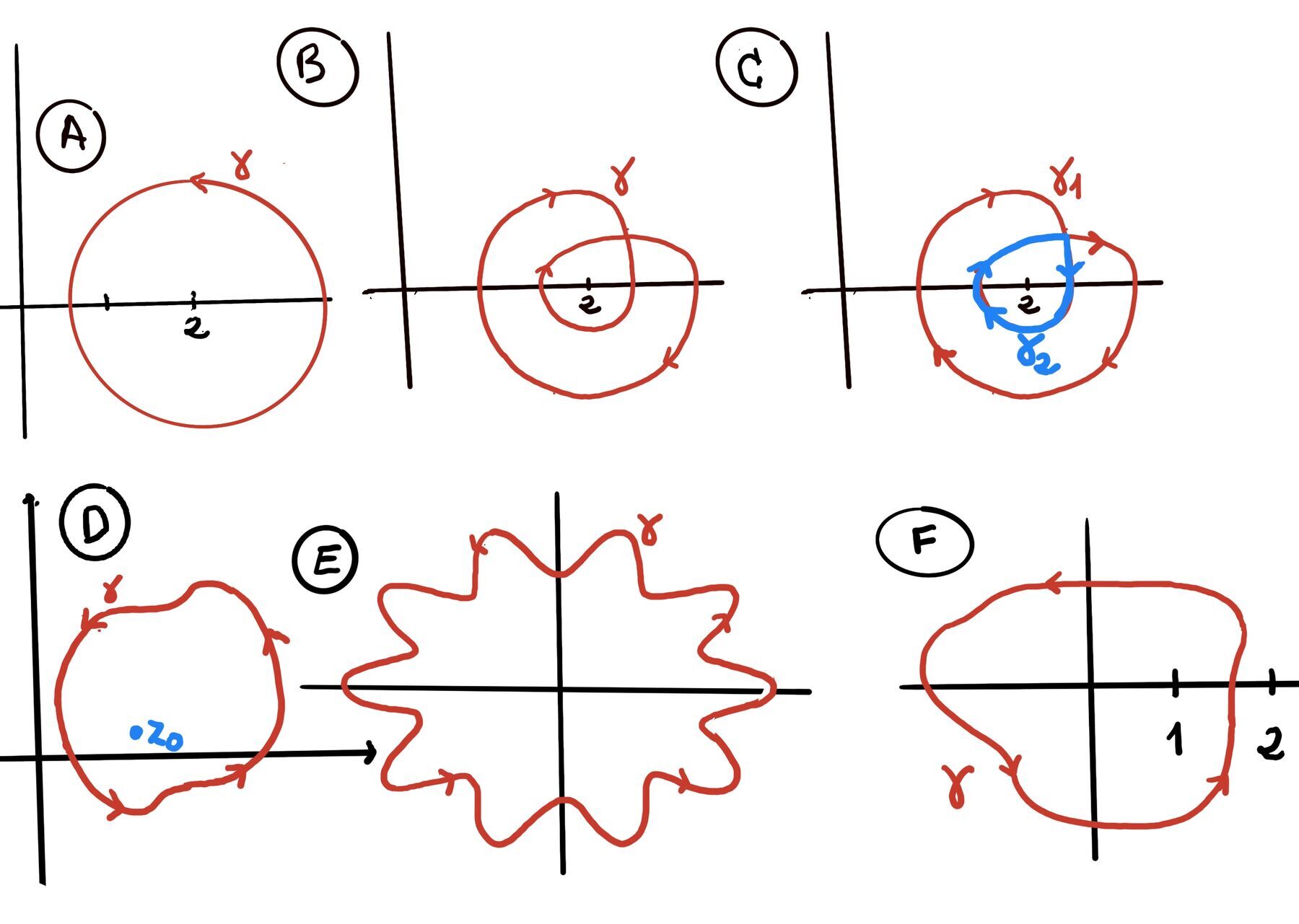
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

• Cauchy’s Theorem for simply connected domains. If a function f is analytic (a function that is complex-differentiable at every point within a domain, i.e., well-behaved and smooth, with no sharp corners, breaks, or singularities like division by zero) throughout a simply simple connected domain D then $\oint_C f(z)dz = 0$ for every closed contour C lying in D.

• General Cauchy Theorem for Multiply Connected Domains. Let $R$ be the multiply connected region (with n holes) inside $C$ but outside of every $C_k$ (each $C_k$ surrounds only one hole in the domain), $R = Int(C) \setminus \bigcup_{k=1}^n \overline{​Int(C_k​)}$​, and let $f(z)$ be analytic on $R$. Now, let $\Gamma$ be any general closed contour (not necessarily simple) that lies entirely in R. This $\Gamma$ can wind around the “holes” (the regions inside each $C_k$) in any way it likes (this is the winding number or index of $\Gamma$ around each hole), the integral over $\Gamma$ is: $\oint_{\Gamma} f(z)dz = \sum_{k=1}^n m_k \oint_{C_k} f(z)dz$.

The Anti-Derivative Theorem

The Anti-Derivative Theorem. Let f be a continuous function on a region G (a region is an open, connected set). Then, the following statements are equivalent:

1. f has an antiderivative F throughout G. This means a function F exists such that F is analytic and F’(z) = f(z) for any z ∈ G.
2. The integral of f over every closed contour $\gamma$ in $G$ is zero: $\oint_\gamma f(z)dz = 0$.
3. The integral of $f$ is path independence. For any two points $a$ and $b$ in $G$, the value of $\oint_\gamma f(z)dz$ is the same (constant) for any contour $\gamma$ in $G$ that starts at a and ends at b.

Cauchy’s Theorem for a disk

Cauchy’s Theorem for a disk. If a function f(z) is analytic in an open disk $D = B(z_0; \delta)$ (a disk centered at $z_0$ with radius $\delta$), then the contour integral for any closed contour γ lying entirely in $B(z_0; \delta)$ is zero, $\oint_{\gamma} f(z)dz = 0.$

It’s the key step that generalizes Cauchy’s theorem from a specific shape (like a rectangle) to any loop within a “safe” region (a disk).

Proof.

Let z = (x, y) be an arbitrary point in the disk $B(z_0; \delta), z_0 = (x_0, y_0)$. We could construct a rectangle inside the disk. We denote γ₁ the L-shaped anti-clockwise path from z to z₀ consisting of a horizontal line segment (σ₁ go from $z_0 = (x_0, y_0) \text{ to } (x, y_0)$) followed by a vertical segment (σ₂ go from $(x, y_0) \text{ to } z = (x, y)$) and γ₂ the L-shaped clockwise path from z to z₀ consisting of a vertical line segment (σ₃ go from $z_0 = (x_0, y_0) \text{ to } (x_0, y)$) followed by a horizontal segment (σ₄ go from $(x_0, y) \text{ to } z = (x, y)$) (Figure i).

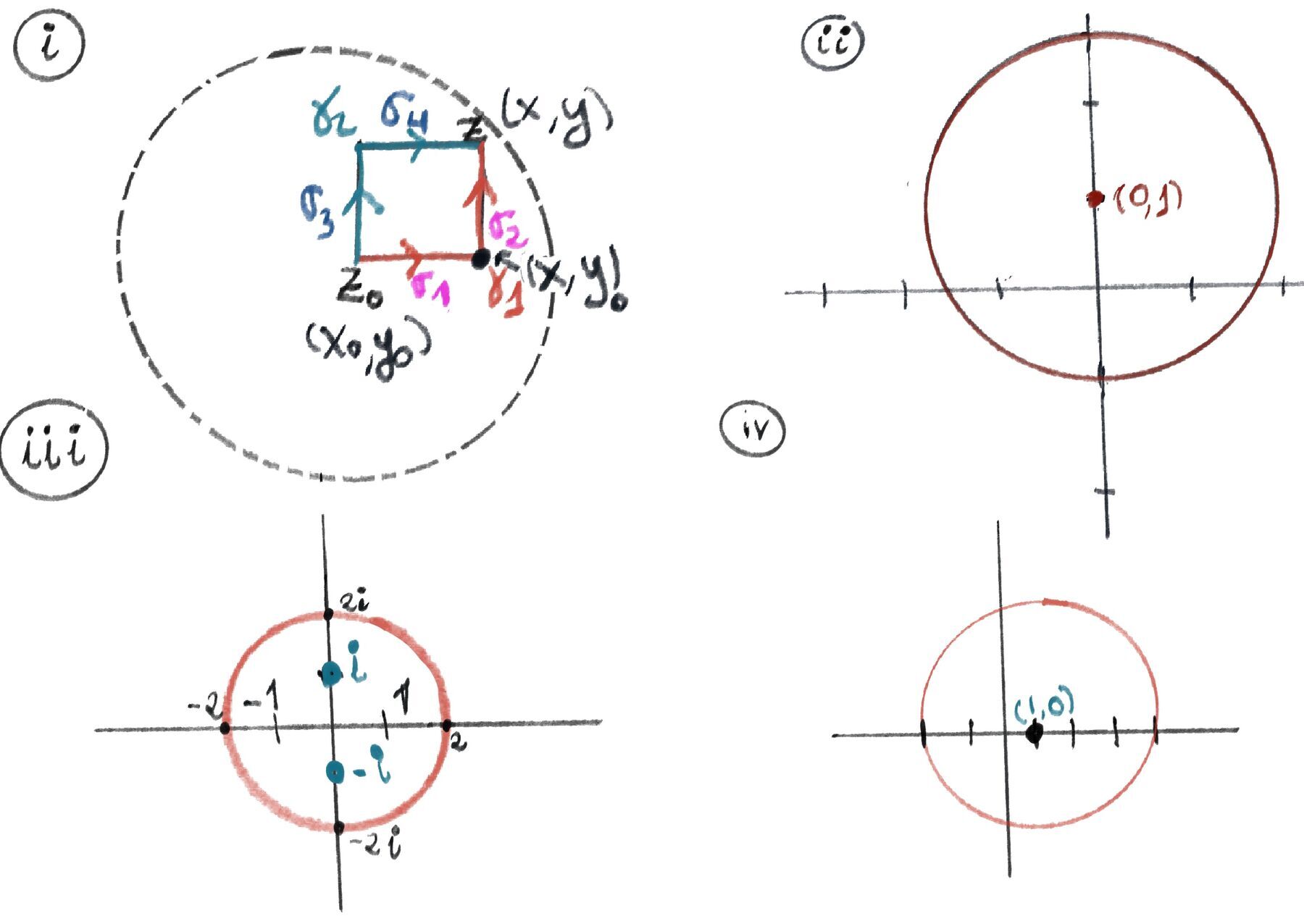
γ₁-γ₂ is the boundary of a rectangular region. So by Cauchy’s Theorem for a rectangle, which states that $\oint_R f(z)dz = 0$ for any closed rectangle $R$ whose interior is also in $D$, $\oint_{\gamma_1 - \gamma_2}f(z)dz = 0 \leadsto[\text{ Linearity of contour integrals}] \oint_{\gamma_1} f(z)dz = \oint_{\gamma_2} f(z)dz$.

The proof’s goal is to show that $f(z)$ has an antiderivative $F(z)$ (a function where $F'(z) = f(z)$) everywhere inside the disk $D$. We will define our potential antiderivative $F(z)$ as an integral from $z_0$ to $z, F(z) = \int_{z_0}^z f(\xi)d\xi$. Our function $F(z)$ is well-defined. It doesn’t matter if we use the H-V path ($\gamma_1$) or the V-H path ($\gamma_2$); the value of $F(z)$ is the same.

$F(z) = \int_{z_0}^z f(\xi)d\xi = \oint_{\gamma_1} f(ξ)dξ = \oint_{\gamma_1} f(ξ)dξ \text{ for } z \in B(z_0; \delta)$.

We will show $F(z)$ is analytic by showing it satisfies the Cauchy-Riemann (C-R) equations and has continuous partials. The C-R equations for $F$ are $U_x = V_y$ and $U_y = -V_x$.

Calculating $\frac{\partial F}{\partial x}$. To find the partial derivative with respect to $x$, it’s easiest to use the V-H path ($\gamma_2$) expression, because the variable $x$ only appears in the second integral (x is the upper limit).

$$ \begin{aligned} F(z) = \oint_{\gamma_2} f(ξ)dξ &=\oint_{\sigma_3} f(ξ)dξ + \oint_{\sigma_4} f(ξ)dξ \\[2pt] &\text{Let's parameterize it:} \\[2pt] &=\int_{t=y_0}^y f(x_0 + it)\cdot 1 \cdot i \cdot dt + \int_{t=x_0}^x f(t + iy)\cdot i \cdot dt. \end{aligned} $$

Now, differentiate with respect to $x, \frac{\partial F}{\partial x} = 0 + \frac{\partial}{\partial x} \left[ \int_{x_0}^x f(t+iy) dt \right]$

By the Fundamental Theorem of Calculus (for real variables), the derivative of an integral with respect to its upper limit is just the integrand evaluated at that limit, $\frac{\partial F}{\partial x} = f(x+iy) = f(z)$

First Fundamental Theorem of Calculus. Let f be a real-valued function that is continuous on an interval [a, b]. Define a function F by $F(x) = \int_a^x f(t)dt$ for $x \in [a, b]$. Then, F is differentiable on (a, b), and F’(x) = f(x). In other words, the derivative of the integral from a to x of f(t) is just f(x).

Calculating, $\frac{\partial F}{\partial y}$. To find the partial derivative with respect to $y$, it’s easiest to use the H-V path ($\gamma_1$) expression.

$$ \begin{aligned} F(z) = \oint_{\gamma_1} f(ξ)dξ &=\oint_{\sigma_1} f(ξ)dξ + \oint_{\sigma_2} f(ξ)dξ \\[2pt] &\text{Let's parameterize it:} \\[2pt] &=\int_{t=x_0}^x f(t+iy_0)\cdot 1 \cdot dt + \int_{t=y_0}^y f(x+it)\cdot i \cdot dt. \end{aligned} $$

Now, differentiate with respect to $y, \frac{\partial F}{\partial y} = 0 + \frac{\partial}{\partial y} \left[ \int_{y_0}^y f(x+it) i dt \right]$

By the Fundamental Theorem of Calculus again: $\frac{\partial F}{\partial y} = f(x+iy) \cdot i = i f(z)$

We have found the partial derivatives of $F(z), \frac{\partial F}{\partial x} = f(z), \frac{\partial F}{\partial y} = i f(z)$. From this, we can see that $\frac{\partial F}{\partial y} = i \frac{\partial F}{\partial x}$, which is a compact form of the C-R equations.

Let’s check explicitly: Let F = U + iV, f = u + iv, and we know $\frac{\partial F}{\partial x} = f(z), \frac{\partial F}{\partial x} = U_x + iV_x = u + iv \implies U_x = u, V_x = v$

$\frac{\partial F}{\partial y} = i f(z), \frac{\partial F}{\partial y} = U_y + iV_y = i(u+iv) = -v + iu \implies U_y = -v, V_y = u$

Check C-R: $U_x = u$ and $V_y = u \implies U_x = V_y, U_y = -v$ and $V_x = v \implies U_y = -V_x$.

The partials of $F$ (which are $u, v, -v, u$) are continuous because $f=u+iv$ is analytic, and analytic functions are continuous.

Conclusion: $F(z)$ satisfies the C-R equations and has continuous partials, so $F(z)$ is analytic in the disk $D$ and F’(z) = f(z).

---

For any analytic function $F(z)$, its complex derivative $F'(z)$ is always equal to its partial derivative with respect to $x, F'(z) = \frac{\partial F}{\partial x}$

The derivative $F'(z)$ is defined by the limit:$F'(z) = \lim_{\Delta z \to 0} \frac{F(z + \Delta z) - F(z)}{\Delta z}$.

For $F(z)$ to be analytic, this limit must be the same no matter which direction or path $\Delta z$ takes as it approaches 0.

Choosing a Convenient Path (The Horizontal Path). Let’s choose the simplest possible path for $\Delta z \to 0$: a horizontal one. This means $\Delta z$ is a purely real number, so we can write $\Delta z = \Delta x$. Plugging this into the limit definition: $F'(z) = \lim_{\Delta x \to 0} \frac{F(z + \Delta x) - F(z)}{\Delta x}$

This is exactly the definition of the partial derivative $\frac{\partial F}{\partial x}$ and we have successfully calculated this exact partial derivative: $\frac{\partial F}{\partial x} = f(z)$.

---

Thus, f has an antiderivative throughout the disk $B(z_0; \delta)$. By the antiderivative theorem (1)⇒(2), the integral of $f$ over any closed contour $\gamma$ in $D$ must be zero, $\oint_{\gamma} f(z)dz = 0$.

Examples and counterexamples

• Entire function, any disk. Let f(z) = $e^{z^3}$, γ : |z–1| = 5. Since f(z) is an entire function (analytic everywhere in $\mathbb{C}$), it is certainly analytic on and inside the circle $\gamma: |z-1|=5.$ By Cauchy’s theorem for a disk [$\oint_γ f(z) dz = 0$ provided f is analytic in the whole open disk that carries γ.], $\oint_{\gamma} e^{z^3}dz = 0$.

  $e^z$ is entire, and since the composition of entire functions is entire, $e^{z^3}$ is also entire. This means $f(z) = e^{z^3}$ has no singularities anywhere in \mathbb{C}.

• Any entire function will behave exactly like the previous example $f(z)=e^{z^3}$: the contour integral around any circle vanishes by Cauchy’s theorem for a disk, since there are no singularities anywhere in $\mathbb{C}$, e.g., $e^z; e^{z^n}; \sin(z); \cos(z); \sin(z^2); \cos(e^z); e^{\sin(z)}; P(z)$ where P is any polynomial and $n \in \mathbb{N}$.

• Polynomial, any disk. Polynomials are entire, so $f(z)=z^4-3z+7$ is analytic everywhere. Circle: $\gamma$: |z+2i|=0.3 is a closed curve contained in the domain of analyticity. By Cauchy’s theorem for a disk [$\oint_γ f(z) dz = 0$ provided f is analytic in the whole open disk that carries γ.], $\oint_{\gamma} z^4-3z+7 dz = 0$.

If you like, you can also see it via an antiderivative $F(z)=\frac{z^5}{5}-\frac{3}{2}z^2+7z;$ the integral of F’ over any closed curve is zero.

• Rational function whose poles miss the disk. The function $f(z)=\frac{1}{z²+ 9} =\frac{1}{(z-3i)(z+3i)}$ has simple poles at $z = \pm 3i$. The circle $\gamma: |z-1|=2$ is centered at 1 and has radius 2. Hence, both poles lie outside the disk $\mathbf{B}(1; 2)$. Since the disk avoids the poles, f is analytic on and inside $\gamma$. By Cauchy’s theorem for a disk [$\oint_γ f(z) dz = 0$ provided f is analytic in the whole open disk that carries γ.], $\oint_{\gamma} \frac{1}{z^2+9} dz = 0$.

• Composition with entire function The function f(z) = cos(sin(z)) is an entire function (sin(z) and cos(w) are entire, and the composition of entire functions is entire; hence f(z) = cos(sin(z)) is entire, analytic everywhere in ℂ), it is certainly analytic on and inside the circle, γ: |z| = 12. By Cauchy’s theorem for a disk [$\oint_γ f(z) dz = 0$ provided f is analytic in the whole open disk that carries γ.], $\oint_{\gamma} cos(sin(z)) dz = 0$.

• Log branch inside a disk avoiding the cut. The principal logarithm Log is analytic on $\mathbb{C}\setminus(-\infty,0]$. For $f(z)=\mathrm{Log}(z+4)$, the excluded set is shifted to the ray $(-\infty,-4]$. $\gamma$: |z| = 1 bounds the disk $\mathbf{B}(0; 1)$. This disk does not intersect the ray $(-\infty,-4]$, since all points in $\mathbf{B}(0; 1)$ have real part greater than -1. Because z + 4 never falls on the principal cut $(-\infty,-4]$ for $z\in \mathbf{B}(0; 1)$, f is analytic on and inside $\gamma$. By Cauchy’s theorem for a disk [$\oint_γ f(z) dz = 0$ provided f is analytic in the whole open disk that carries γ.], $\oint_{\gamma} \mathrm{Log}(z+4) dz = 0$.

• Integral with enclosed poles and residue cancellation. $f(z) = \frac{1}{z²+1}, \gamma: |z| = 2$. Cauchy’s theorem for a disk doesn’t apply because $f(z)=\frac{1}{z^2+1}$ is not analytic on B(0; 2) (it has poles at $z = \pm i$ inside) (Figure iii).

For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.

$\text{Res}\left(\frac{1}{z^2+1}, i\right) = \lim_{z \to i}(z-i)\frac{1}{z^2+1} = \lim_{z \to i} \frac{1}{z+i} = \frac{1}{2i}$

$\text{Res}\left(\frac{1}{z^2+1}, -i\right) = \lim_{z \to -i}(z+i)\frac{1}{z^2+1} = \lim_{z \to -i} \frac{1}{z-i} = \frac{1}{-2i}.$

The Residue Theorem states that the integral of a function f(z) around a simple (doesn’t cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour: $\oint_{|z|=2}\frac{dz}{z^2+1} = 2\pi i \sum Res(f, z_k) = 2\pi i\left(\frac{1}{2i}+\frac{1}{-2i}\right) = 0,$ so the contour encloses both simple poles with opposite residues, yielding cancellation.

• Counterexample. Evaluate $\oint_C \frac{1}{z^2 + 4}$ where C is a circle |z - i| = 2.

The curve C is the circle centered at i (0, 1) with radius 2 (Figure ii). We know that $a^2 - b^2 = (a + b)(a - b)$. Then, we have $\frac{1}{z^2 + 4} = \frac{1}{z^2 - (2i)^2} = \frac{1}{(z + 2i)(z - 2i)}$.

F(z) is not analytic at z = ±2i and 2i lies inside the circle, so we cannot apply the Cauchy’s Theorem for a disk.

Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$

$F(z) = \frac{1}{(z + 2i)(z - 2i)} = \frac{\frac{1}{z+2i}}{z-2i} = \frac{f(z)}{z -2i} \text{ where we define } f(z) = \frac{1}{z+2i}$.

Clearly, f(z) is analytic inside and on the closed curve C (only z = 2i lies inside C). By Cauchy’s Integral Formula, $\oint_C \frac{1}{z^2 + 4} = 2\pi i f(2i) = 2\pi i \cdot \frac{1}{4i} = \frac{\pi}{2}$

• Evaluate $\oint_C \frac{e^{2z}}{(z+1)^4}$ where C is |z -1| = 3.

C is a circle with center (1, 0) and radius 3. $\frac{e^{2z}}{(z+1)^4}$ is not analytic at z = -1 because this singularity lies inside the circle C (Figure iv).

Let f(z) = $e^{2z}$, f is analytic inside and on the circle C. Then, by the extension of Cauchy’s Integral Formula, $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$ where f(z) = $e^{2z}, n = 3, z_0 = -1$.

$\frac{e^{2z}}{(z+1)^4} = \frac{f(z)}{(z+1)^4} = \frac{2\pi i}{3!}f^{(3)}(-1) = \frac{2\pi i}{3\cdot 2}\frac{8}{e^2} = \frac{8\pi i}{3e^2}$

$f'(z) = 2e^{2z}, f''(z) = 4e^{2z}, f'''(z) = 8e^{2z}, f'''(-2) = 8e^{-2}=\frac{8}{e^2}$