Cauchy's Theorem for a Rectangle

Without pain, without sacrifice, we would have nothing, Fight Club.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

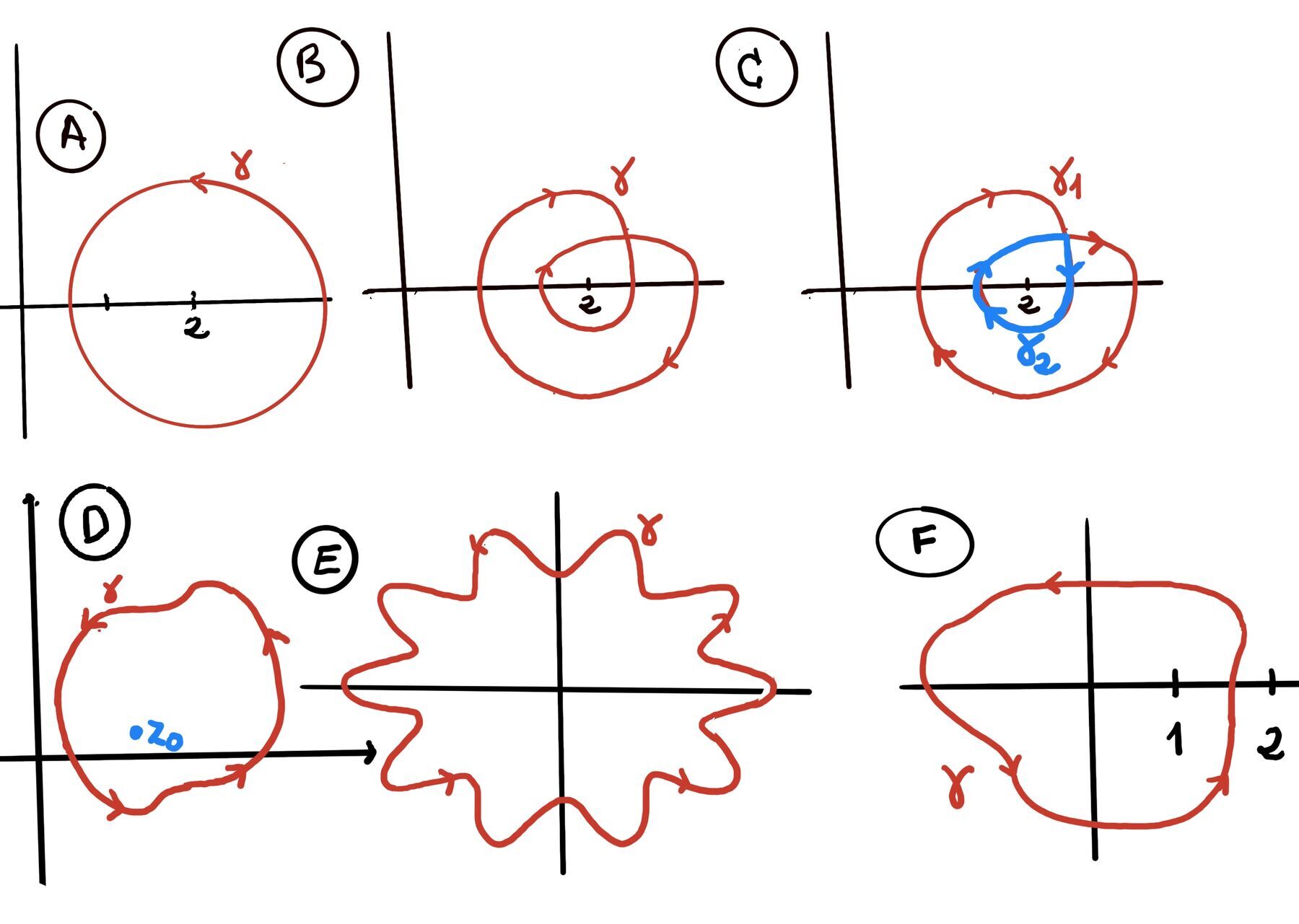
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

Cauchy’s Theorem for a Rectangle

Cauchy’s Theorem for a Rectangle. Let R be a rectangle region R = {x + iy: a ≤ x ≤ b, c ≤ y ≤ d}. Let f be analytic on an open set that contains R (so f is analytic on and in a neighborhood of R). Then, the positively oriented boundary (∂R) contour integral of f vanishes, $\int_{\partial R}f(z)dz = 0$.

Similarly, Let T be a triangular region. Let f be analytic on an open set that contains T (so f is analytic on and in a neighborhood of T). Then, the positively oriented boundary (∂T) contour integral of f vanishes, $\int_{\partial T}f(z)dz = 0$.

Proof.

We are going to subdivide R into four equally sized rectangles (Figure 1). We observe that the contour integrals along the inner boundaries cancel each other out due to opposite orientations (every interior edge is traversed twice in opposite directions). Consequently, the integral over the entire boundary of ∂R can be expressed as the sum of integrals over these smaller rectangles, $\int_{\partial R}f(z)dz = \int_{\partial R_1}f(z)dz + \int_{\partial R_2}f(z)dz + \int_{\partial R_3}f(z)dz + \int_{\partial R_4}f(z)dz$. Let’s name the perimeter and diagonal of R, l and d respectively.

Similarly, we can divide the triangular contour shown in Figure 4, then: $\int_{\partial T}f(z)dz = \int_{\partial T_1}f(z)dz + \int_{\partial T_2}f(z)dz + \int_{\partial T_3}f(z)dz + \int_{\partial T_4}f(z)dz$

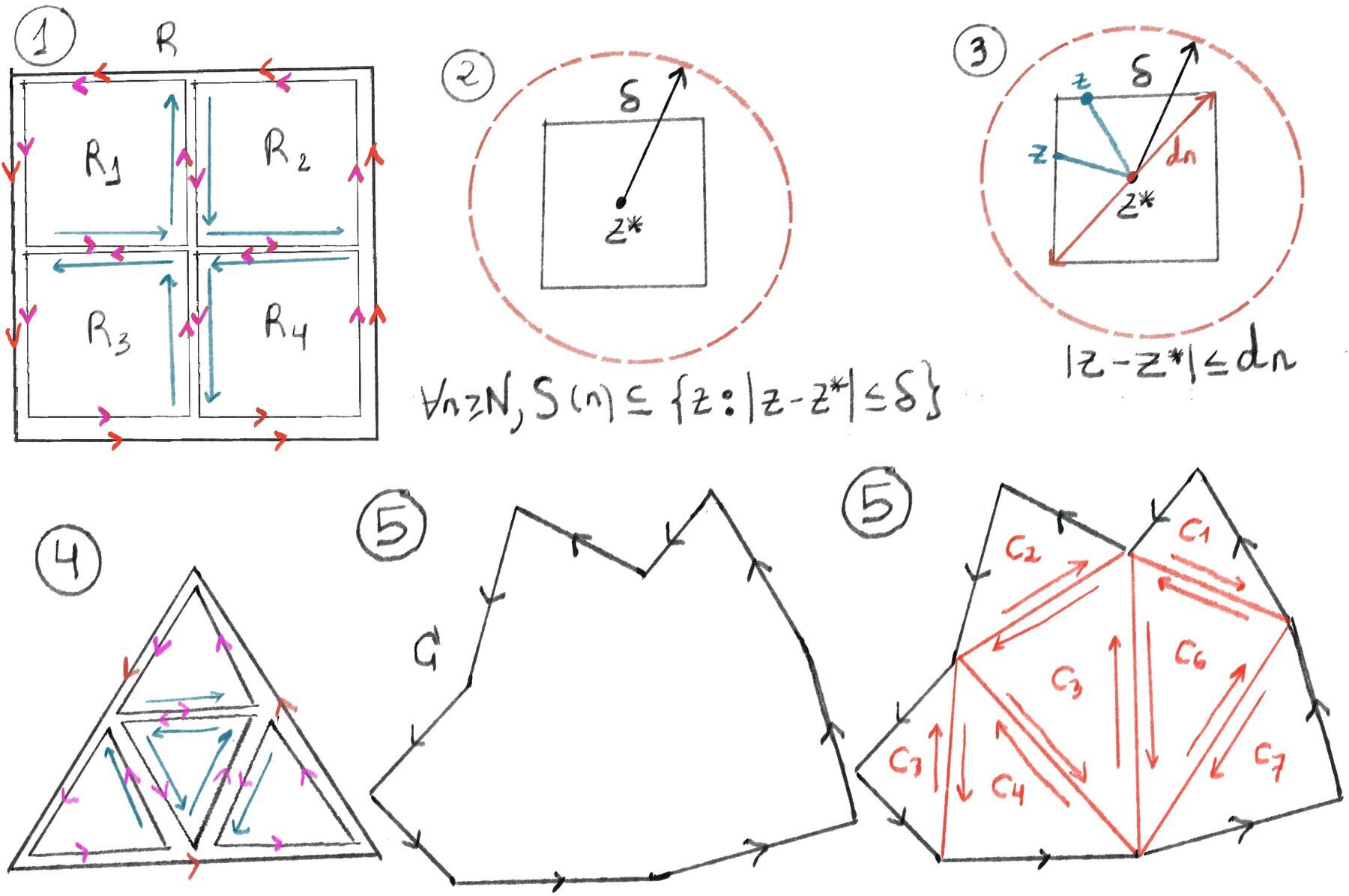
By the triangle inequality, at least one of these subrectangle (or subtriangle), say $R_i$ or call it S(1), must contribute at least one-fourth of $\int_{\partial R}f(z)dz$ in absolute value, we can apply this reasoning recursively.

$|\int_{\partial R}f(z)dz| \le |\int_{\partial R_1}f(z)dz| + |\int_{\partial R_2}f(z)dz| + |\int_{\partial R_3}f(z)dz| + |\int_{\partial R_4}f(z)dz|$

The proof is essentially the same in both cases. For the sake of simplicity, we will prove it for rectangle regions.

The process involves continually subdividing the rectangle R into smaller rectangles, each time ensuring that the modulus of the integral remains bounded by a diminishing quantity.

Note. If every $|\int_{\partial R_k}f(z)dz|$ were $\le \frac{1}{4}|\int_{\partial R}f(z)dz|$, their sum could not reach $|\int_{\partial R_k}f(z)dz|$.

$|\int_{\partial R_i}f(z)dz| \ge \frac{1}{4}|\int_{\partial R}f(z)dz|$. Let’s call it $S(1)$. If there is more than one of such rectangles for which this inequality holds, then choose one of them arbitrarily. Divide $S(1)$ into four equal rectangles, $R_1^1, R_1^2, R_1^3, R_1^4$, there exists an i, $1 \le i \le 4, \text{ s.t. } |\int_{\partial R_1^i}f(z)dz| \ge \frac{1}{4}|\int_{\partial R_1}f(z)dz| \ge \frac{1}{4}\cdot \frac{1}{4}|\int_{\partial R}f(z)dz|$. Let’s call this rectangle $R_1^i$ as S(2).

Continuing by induction, we obtain a sequence of rectangles with

• $S(n+1) \subseteq S(n)$ for all n, this process leads to a nested sequence of rectangles.
• $|\int_{\partial S(n)}f(z)dz| \ge \frac{1}{4^n}|\int_{\partial R}f(z)dz|$
• The perimeter of S(n) is $d_n = \frac{d}{2^n}$. The diagonal of S(n) is $l_n = \frac{l}{2^n}$.

Cantor’s Intersection Theorem (Metric Space Version). Let (X, d) be a complete metric space (like $\mathbb{R}^n$). Suppose $\{S(n)\}_{n=1}^\infty$ is a sequence of non-empty, closed, and bounded subsets of X such that:

• The sequence is nested: $S(n+1) \subseteq S(n)$ for all n,
• The diameter of the sets tends (shrinks) to zero: $\lim_{n \to \infty} \text{diameters}(S(n)) = 0.$

Then, their intersection is a single point $\bigcap_{n=1}^\infty S(n)$ contains exactly one point, $z^*$.

Given any $\delta > 0$, we can find a corresponding natural number N such that $S(N) \subseteq \{ z : |z - z^*| \le \delta \}$, i.e., $\forall n \ge N, S(n) \subseteq \{ z : |z - z^*| \le \delta \}, | f(z) - f(z^*) | \le \delta$

Utilizing the definition of analyticity, we can explore the behavior of f(z) near the point $z^*$. Analyticity implies complex differentiability at $z^*$. Given any $\epsilon > 0$, we can find a corresponding $\delta > 0$ such that the modulus of the difference between f(z) and its Taylor expansion around $z^*$ is less than $\epsilon|z-z^*|, \text{ i.e. } |f(z) - f(z^*) - f'(z^*)(z-z^*)| \le \epsilon|z-z^*|$ when z is within $\delta$ of $z^*, |z-z^*| \le \delta$. This is because $\lim_{z \to z^*} \frac{f(z) - f(z^*)}{z-z^*} = f'(z^*) ⇔ \lim_{z \to z^*} \frac{f(z) - f(z^*) - f(z^*) (z-z^*)}{z-z^*} = 0$.

Therefore, given any $\epsilon > 0$, choose the corresponding $\delta > 0$ such that $|f(z) - f(z^*) - f'(z^*)(z-z^*)| \le \epsilon|z-z^*|$. Using this very $\delta$, obtain an N such that $S(N) \subseteq \{ z : |z - z^*| \le \delta \}$. For n ≥ N, on ∂S(n) we have $|f(z) - f(z^*) - f'(z^*)(z-z^*)| \le \epsilon|z-z^*|$

By the Fundamental Theorem of Calculus, we know that $\int_{\partial S(n)} 1dz = 0, \int_{\partial S(n)} zdz = 0$ (*)

Constant and linear terms vanish. $\int_{\partial S} 1dz = 0, \int_{\partial S} zdz = 0$ for any closed contour S because the antiderivatives are z and $\frac{z²}{2}$.

$|f(z) - f(z^*) - f'(z^*)(z-z^*)| \le \epsilon|z-z^*| \leadsto |\int_{\partial S(n)}f(z) - f(z^*) - f'(z^*)(z-z^*)dz| \le |\int_{\partial S(n)}\epsilon(z-z^*)dz|$

Hence, $|\int_{\partial S(n)}f(z)dz - \int_{\partial S(n)}f(z^*)dz - f'(z^*)\int_{\partial S(n)}zdz + f'(z^*)z^*\int_{\partial S(n)}dz| \le \epsilon\int_{\partial S(n)} |z-z^*||dz|$

Many terms are zeros (*), so we get: $|\int_{\partial S(n)}f(z)dz| \le \epsilon\int_{\partial S(n)} |z-z^*||dz|$

Using the estimation lemma, $|\int_{\partial S(n)}f(z)dz| \le \epsilon d_n l_n$ because the distance $|z-z^*|$ is less than the diagonal of $S(n), |z-z^*| \le d_n$. As we previously stated $d_n = \frac{d}{2^n}, l_n = \frac{l}{2^n} \leadsto |\int_{\partial S(n)}f(z)dz| \le \epsilon 4^{-n}d\cdot l$.

Therefore, $4^{-n}|\int_{\partial R}f(z)dz| \le |\int_{\partial S(n)}f(z)dz| \le \epsilon 4^{-n}d\cdot l$

Ignoring the intermediate term $4^{-n}|\int_{\partial R}f(z)dz| \le \epsilon 4^{-n}d\cdot l \leadsto [\text{Multiply by } 4^n] |\int_{\partial R}f(z)dz| \le \epsilon d\cdot l$.

Since $\epsilon$ is arbitrary, $|\int_{\partial R}f(z)dz| = 0 \leadsto \int_{\partial R}f(z)dz = 0.$

Remarks and extensions

• Once we believe the rectangle case, we get every simple polygon for free by a tiling or triangulation argument. In other words, $\int_{\partial C}f(z)dz = 0$ for any positively oriented simple polygon C (non-self-intersecting, closed) when f is analytic on an open set that contains C (so f is analytic on and in a neighborhood of C) (Figure 5).

There are several forms of Cauchy’s theorem. If C is a closed polygonal contour lying entirely within a simply connected domain D, f is a complex function analytic in D, then $\int_{\partial C}f(z)dz = 0$.

1. Tile or triangulate the interior of the polygon C, meaning that the closed polygon C can be decomposed into a finite number of rectangles (tiles) or triangles.
2. Orient Boundaries Positively. Assign counterclockwise orientation to each $\partial C_k$, consistent with C’s positive orientation.
3. Sum Integrals with Cancellation. Integrate f over the boundary of every tile. On each interior edge the path is traversed once in each direction by the two adjacent tiles or subtriangles, so those contributions cancel. What remains is exactly the integral over the outer perimeter ∂C, $\int_{C}f(z)dz = \sum_{k=1}^n \int_{C_k}f(z)dz$
4. By the rectangle (triangle) theorem each individual integral is zero (f holomorphic inside $C_k$); hence their sum is zero; hence $\int_{\partial C}f(z)dz = 0.$

• Cauchy’s Theorem for Rectifiable Jordan Curves. Let Γ be a rectifiable Jordan curve and let f be analytic on an open set Ω containing Γ ∪ Int(Γ). Then, $\oint_{\Gamma} f(z)dz = 0.$

Examples

• For entire functions (analytic everywhere in ℂ) such as f(z) = $e^z, z^2+7, sin(z)$, the integral over any rectangle, triangle, or polygon P vanishes, $\int_{\partial P}f(z)dz = 0.$ This follows because entire functions satisfy the analyticity condition everywhere and any such contour lies in a simply connected domain (the entire complex plane).
• Functions with isolated singularities. For f(z) = 1/z, this function is analytic everywhere except at z = 0 and the theorem does not apply if 0 ∈ Int(R). If the rectangle R does not contain 0 in its interior (i.e., 0 ∉ Int(R)), then f is analytic on an open set containing R, and thus, $\int_{\partial R}\frac{1}{z}dz = 0$. If 0 is in the interior of R (0 ∈ Int(R)), then the theorem does not apply. By the residue theorem, $\int_{\partial R}\frac{1}{z}dz = 2\pi i$ when the rectangle winds once counterclockwise around 0. This illustrates how singularities inside contours usually lead to non-zero integrals.
• Non-simply connected domains: Let D = ℂ \ {0} (punctured plane). This domain is not simply connected. Consider f(z) = 1/z, which is analytic in D. For the unit circle C (a closed contour in D), $\int_{\partial R}\frac{1}{z}dz = 2\pi i \ne 0$. This demonstrates that the simply connected condition is essential for Cauchy’s theorem to hold.
• Exponential with singularity: For $f(z) = e^z/(z-a)$, if a is inside a triangular contour T, then $\int_{\partial T}e^z/(z-a)dz = 2\pi i e^a$ by Cauchy’s integral formula. If a is outside T, then $\int_{\partial T}e^z/(z-a)dz = 0$ since f is analytic on an open set containing T.