Cauchy's Integral Theorem: Classical Green-proof, Goursat upgrade, deformation principle, and corollaries

When the world says, ‘Give up,’ hope whispers, ‘Try it one more time,’ Lyndon B. Johnson.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

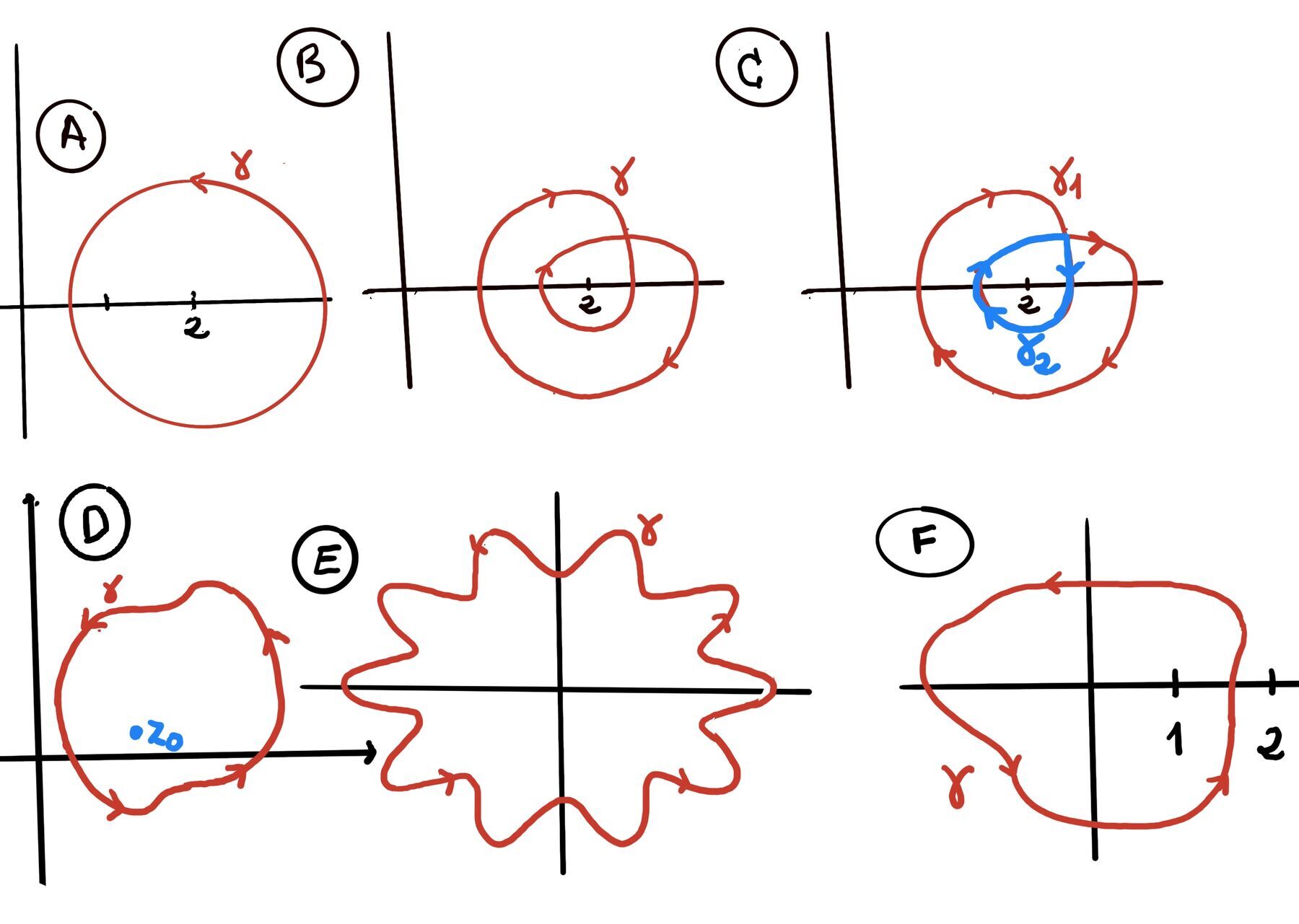
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

At its core, Cauchy’s Integral Theorem is a profound statement about the nature of “well-behaved” complex functions. It says that if a function is analytic (differentiable at every point in a open set), then integrating it around any simple closed loop within that region will always yield a result of zero. Analytic functions are so “smooth” and well-behaved that their integrals over closed loops vanish (when you walk a closed loop in a region where f is analytic, positive contributions cancel negative ones, so the net integral is zero).

Let’s break down the conditions mentioned:

• The domain Ω (it is connected — meaning any two points in D can be joined by a continuous path that lies entirely within D) is required to be an open subset (a set that doesn’t include its boundary — every point in the set has some “wiggle room” around it. $∀x \in Ω, ∃ \varepsilon > 0 \text{ such that } B(x, \varepsilon) = \{y \in \mathbb{R}^n : |y - x| < \varepsilon\} \subset \mathbb{C}$). A function f is analytic (or holomorphic) at a point if it is complex differentiable in some neighborhood of that point. If Ω were not open, there could be points on its boundary where f is defined but not differentiable in a full disk around them.
• The function f = u + iv is analytic in Ω, meaning the function is smooth in the complex sense, which imposes a very rigid structure on its real (u) and imaginary (v) parts. f(z) must be differentiable at every point in Ω. Common analytic functions include polynomials ($f(z) = z^2 + 3z + 1, f(z) = z^3 -2z$), exponentials ($f(z) = e^z$), and trigonometric functions (sin(z), cos(z)).
• Partial derivatives are continuous: This is a technical condition needed to use Green’s Theorem. A more powerful version of this theorem, called the Cauchy-Goursat Theorem, proves this condition isn’t even necessary —analyticity alone is enough.
• The contour γ is a simple (a path does not intersect itself. A circle or a square is simple; a figure-eight is not) closed contour (the path starts and ends at the same point, forming a complete loop), piecewise C¹ (smooth except at finitely many points), positively oriented (counterclockwise), and the entire curve and its interior must lie within a larger open domain Ω ($\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$) where the function is analytic (the location must be safe), e.g., a circle, a rectangle, a distorted ellipse, or polygon. There can be no singularities (problem points) on the path or anywhere inside it.

Proof:

Step 1: It translates the abstract complex integral into the language of real multivariable calculus.

u = u(x, y), v = v(x, y), z = x + iy, dz = dx + idy. We replace f(z) with its real and imaginary parts, u + iv, and the complex differential dz with its components, dx + idy.

$\oint_{\gamma} f(z)dz = \oint_{\gamma} (u + iv)(dx + idy) = \oint_{\gamma} (udx -vdy) + i(udy + vdx) = \oint_{\gamma} (udx -vdy) + i\oint_{\gamma}(udy + vdx).$

Step 2: Apply Green’s Theorem (the boundary is oriented counterclockwise). It states that for a vector field F = (P, Q), the line integral $\oint_{\gamma} (Pdx + Qdy)$ is equal to the double integral $\int\int_{Int(\gamma)} (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dA$, where Int(γ) is the region inside the contour γ.

For the Real Part, we have P = u, Q = -v, applying Green’s Theorem, the integrand becomes $(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}) = (\frac{\partial (-v)}{\partial x}-\frac{\partial u}{\partial y}) = (\frac{-\partial v}{\partial x}-\frac{\partial u}{\partial y})$. For the Imaginary Part, we have P = v, Q = u, applying Green’s Theorem, the integrand becomes $(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}) = (\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y})$

$= \int\int_{Int(\gamma)} (\frac{-\partial v}{\partial x}-\frac{\partial u}{\partial y})dxdy + i\int\int_{Int(\gamma)} (\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y})dxdy$

Step 3: Use the Cauchy-Riemann Equations. An analytic function f = u + iv must satisfy the Cauchy-Riemann equations: $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$.

By Cauchy-Riemann equations, $= \int\int_{Int(\gamma)} 0dxdy + i\int\int_{Int(\gamma)} 0dxdy = 0 + i\cdot 0 = 0$.

Since both integrands are identically zero everywhere inside the contour, the double integrals over that area must both be zero.

Corollaries

• Path independence on simply connected domains. If f is analytic on a simply connected domain D, then $\int_\gamma f(z) dz$ depends only on the endpoints; equivalently, every closed contour integral is 0.

Theorem: If a function f(z) is analytic throughout a simply connected domain D, then f(z) is guaranteed to have an antiderivative (also called a primitive), F(z), in D, meaning we can always find a function F(z) such that F′(z) = f(z).

This step relies on the domain being simply connected; if there were holes, an antiderivative might not exist.

Once we know an antiderivative F(z) exists, we can use the Fundamental Theorem of Calculus for Contour Integrals. This theorem states that if f(z) has an antiderivative F(z), then the integral of f(z) from a point $z_1$ to a point $z_2$ is simply: $\int_{z_1}^{z_2} f(z)dz = F(z_2) - F(z_1).$

A closed contour is a path where the start and end points are the same, $z_1 = z_2$. Plugging this into the formula from the Fundamental Theorem: $\oint_{\gamma} f(z)dz = \int_{z_1}^{z_2} f(z)dz = F(z_2) - F(z_1) = 0$.

In summary, the corollary follows this logical chain:

1. Analytic in a simply connected domain ⟹ An antiderivative F(z) exists.
2. An antiderivative exists ⟹ The integral is path-independent and depends only on the endpoints $\oint_{\gamma} f(z)dz = \int_{z_1}^{z_2} f(z)dz = F(z_2) - F(z_1)$.
3. Path independence ⟹ The integral over any closed loop is zero.

• Existence of antiderivatives. If every closed contour integral of an analytic function f in a domain D is zero, then f has an antiderivative F in D, i.e., F′(z) = f(z) for all z∈D.

Proof:

Let’s define F(z) = $\int_{z_0}^z f(w)dw$. F(z) is well-defined ↔ Path independence. Let’s take two different paths, γ₁ and γ₂, from z₀ to z. Now, create a new closed loop γ by going from z₀ to z along γ₁ and then returning from z to z₀ along the reverse of γ₂ (denoted -γ₂), γ = γ₁-γ₂. By our starting condition, the integral around this closed loop must be zero, $\oint_{\gamma} f(w)dw = 0$. By linearity, $\oint_{\gamma} f(w)dw = \oint_{\gamma_1} f(w)dw -\oint_{\gamma_2} f(w)dw = 0 \leadsto \oint_{\gamma_1} f(w)dw = \oint_{\gamma_2} f(w)d$. This proves that the integral only depends on the endpoints, not the path, and our definition for F(z) is well-defined and gives a single, unique value for each z.

Now we have to show that this function F(z) is actually the antiderivative of f(z). We do this using the formal limit definition of a derivative: F’(z) = $\lim_{h \to 0} \frac{F(z+h)-F(z)}{h}$.

Our task is to show that: $F'(z) = \lim_{h \to 0} \frac{F(z+h)-F(z)}{h} = f(z)$ where $F(z+h)-F(z) = \int_{z_0}^{z+h} f(w)dw - \int_{z_0}^z f(w)dw$.

Using path independence, we can choose the path from z₀ to z+h to go via z. Specifically, we go from z₀ to z and then from z to z+h along a straight line segment, $\int_{z_0}^{z+h} f(w)dw = \int_{z_0}^{z} f(w)dw + \int_{z}^{z+h} f(w)dw$.

Then, $F(z+h)-F(z) = \int_{z_0}^{z+h} f(w)dw - \int_{z_0}^z f(w)dw = \int_{z_0}^{z} f(w)dw + \int_{z}^{z+h} f(w)dw - \int_{z_0}^z f(w)dw$

The first and last terms cancel, leaving us with a very simple result: $F(z+h)-F(z) = \int_{z}^{z+h} f(w)dw$, hence F’(z) = $\lim_{h \to 0} \frac{F(z+h)-F(z)}{h} = \lim_{h \to 0} \frac{\int_{z}^{z+h} f(w)dw}{h} = \lim_{h \to 0} \frac{1}{h}\int_{z}^{z+h} f(w)dw$. We want to show this limit equals f(z).

Let’s consider the expression $(\frac{1}{h}\int_{z}^{z+h} f(w))-f(z)$. Notice that $f(z) = \frac{1}{h}\int_{z}^{z+h} f(z)dw$ (Integrating a constant f(z) along a path of length h gives f(z)·h). Therefore,

$(\frac{1}{h}\int_{z}^{z+h} f(w))-f(z) = \frac{1}{h}\int_{z}^{z+h} f(w) - \frac{1}{h}\int_{z}^{z+h} f(z)dw =\frac{1}{h} \int_{z}^{z+h} [f(w) - f(z)]dw$.

Since f is analytic, it is continuous. This means that as w gets close to z, f(w) gets close to f(z). For any small ε > 0, there exists δ > 0 such that: ∣w − z∣ < δ ⇒ |f(w) - f(z)| < ε.

Now, if ∣h∣ < δ, then for all w on the straight-line segment from z to z + h, we have ∣w − z∣ ≤ ∣h∣ < δ, so: |f(w) - f(z)| < ε.

Using the ML-Inequality on the integral part: M = max{∣f(w)−f(z)∣: w on the segment}. Then, M < ε. L = Length of the path or segment from z to z + h, which is |h|.

Thus, $|\frac{1}{h} \int_{z}^{z+h} [f(w) - f(z)]dw| = \frac{1}{|h|}|\int_{z}^{z+h} [f(w) - f(z)]dw| \le \frac{1}{|h|}(M \cdot L) \le \frac{1}{|h|} (ε \cdot |h|) = ε$.

We have shown that for any ε > 0, there exists δ > 0 such that if 0 < ∣h∣ < δ, then:

$|\frac{F(z+h)-F(z)}{h}-f(z)| = |\frac{1}{h} \int_{z}^{z+h} [f(w) - f(z)]dw|$ < ε. This is exactly the definition of $\lim_{h \to 0} \frac{F(z+h)-F(z)}{h} = f(z)$, i.e., F′(z) = f(z).

• Deformation of contour. If two closed contours are homologous in a region where f is analytic (you can slide one to the other without crossing singularities), then their integrals are equal. In particular, if one is contractible to a point (no singularities inside), the integral is 0.

It allows us to replace a complicated contour integral with a much simpler one. The core idea is that you can freely change the shape of a contour without changing the value of the integral, as long as the contour does not pass through any singularities of the function, e.g., suppose you need to calculate $\oint_{\gamma_1} \frac{1}{z}dz$ where $\gamma_1$ is a complicated square around the origin.

f(z) = 1/z has a singularity at z = 0. Let $\gamma_2$ be a simple unit circle, ∣z∣ = 1. The function is analytic in the region between the square and the circle. By the Deformation Principle, the difficult integral over the square is equal to the easy integral over the circle: $\oint_{\text{square}} \frac{1}{z}dz = \oint_{\text{circle}} \frac{1}{z}dz = 2\pi \cdot i$

If a contour γ can be shrunk down to a single point without crossing any singularities, it means that the function f(z) is analytic everywhere inside γ. This is just a restatement of the original Cauchy’s Integral Theorem, which tells us the integral must be zero.

Proof:

Let f(z) be analytic in the region between two simple closed contours, γ₁ and γ₂, where both are positively oriented (counter-clockwise). Imagine an outer loop γ₁ and an inner loop γ₂. We create a single, non-intersecting closed path, which we’ll call γ, by adding a “bridge” connecting the two loops.

The new path γ travels: (i) Along the outer contour γ₁ (counter-clockwise). (ii) Down the bridge. (iii)Along the inner contour γ₂ in the opposite (clockwise) direction. We denote this path as −γ₂. (iv) Up the bridge, returning to the start.

The function f(z) is analytic everywhere in the region enclosed by this new path γ. Notice that the singularities (if any) are in the “hole” inside γ₂ (no singularities inside or between both contours), The function f(z) is analytic everywhere in the region enclosed by this new path γ. Notice that the singularities (if any) are in the “hole” inside γ₂ (no singularities inside or between both contours), so they are outside the region we are integrating around.

Because f(z) is analytic inside and on the path γ, Cauchy’s Integral Theorem applies, and the integral is zero: $\oint_{\gamma} f(z)dz = 0$.

The integral over the full path is the sum of its parts: $\oint_{\gamma_1} f(z)dz + \oint_{\text{bridge}} f(z)dz + \oint_{-\gamma_2} f(z)dz + \oint_{\text{-bridge}} f(z)dz = 0$. The integrals along the bridge are taken over the same path but in opposite directions, so they cancel each other out. We are left with: $\oint_{\gamma_1} f(z)dz + \oint_{-\gamma_2} f(z)dz = 0$. Since reversing a path negates its integral, $\oint_{\gamma_1} f(z)dz - \oint_{\gamma_2} f(z)dz = 0 \leadsto \oint_{\gamma_1} f(z)dz = \oint_{\gamma_2} f(z)dz$

• Failure pinpoints singularities. If f is continuous on and inside the simple closed contour γ and $\oint_\gamma f\neq 0$, then f cannot be analytic at every point of Int(γ).

Proof (one paragraph, pure logic).

Assume the opposite: f is analytic on the open set D ⊃ γ ∪ Int(γ). Cauchy’s theorem gives $\oint_{\gamma} f(z)dz = 0$. This contradicts the hypothesis “the integral is non-zero”. Hence the assumption “f analytic throughout Int(γ)” is false, therefore analyticity fails at (at least) one point inside γ.

Classic example: $f(z)=1/z$ on the unit circle, $\gamma(t)=e^{it}, 0 \le t \le 2\pi$. Direct parametrisation: $\oint_{\gamma} f(z)dz = \int_0^{2π} \frac{ie^{it}}{e^{it}} dt = i\int_0^{2\pi} dt = 2\pi i ≠ 0$. The corollary now guarantees that 1/z cannot be analytic everywhere inside the unit disk – and indeed its derivative does not exist at z = 0. Thus, a non-zero integral is an alarm bell: somewhere beneath γ the function is not complex-differentiable.

Examples

• Let $f(z) = z^2$, which is entire (analytic everywhere in $\mathbb{C}$). Compute the integral around the square $\gamma$ with vertices at 0, 1, 1+i, i.

$\oint_C z^2 dz = 0.$ Why? This result is a direct consequence of Cauchy’s Integral Theorem. It states that if a function is analytic (holomorphic) on and inside a simple closed contour, then the integral of the function along that contour is zero.

1. $z^2$ is a polynomial, and polynomials are entire functions —they are analytic everywhere in the complex plane $\mathbb{C}$.
2. The square contour γ is a simple closed curve (it does not intersect itself), piecewise C¹, positively orientated, and lies entirely in $\mathbb{C}$. A square contour will also works.
3. Since the function is analytic everywhere, any path in the complex plane is in a “safe” region.

• Let f(z) = $\frac{1}{z-a}$. f is analytic everywhere except at the point z = a. If the contour γ does not enclose a, then the function f(z) is analytic on the path and at every point inside the path. The conditions of Cauchy’s Theorem are met. $\oint_{\gamma} \frac{1}{z-a} dz = 0$. If γ does enclose a, the theorem does not apply (the function has a singularity inside the contour), and in fact, $\oint_{\gamma} \frac{1}{z-a} dz = 2\pi i$.

Case 1. a outside γ. Then, $\frac{1}{z-a}$ is analytic on and inside γ, so Cauchy’s theorem applies and $\oint_{\gamma} \frac{1}{z-a} dz = 0$.

Case 2. a inside γ (γ winds once counter-clockwise). The integrand is not analytic at a, so Cauchy’s theorem does not apply. $\oint_{\gamma} \frac{1}{z-a} dz = 2\pi i$ when γ is any simple, positively-oriented, piecewise-C¹ closed curve that winds once around the point a.

1 Solution. Direct parametrisation. Because the integrand is analytic except at a, we may deform γ to the circle |z – a| = R without changing the integral (deformation principle). Parametrise that circle by $\gamma(t) = a + R e^{it}, f(\gamma(t)) = \frac{1}{R e^{it}} 0 ≤ t ≤ 2π, \gamma'(t) = iR e^{it}$

Then, $\oint_{\gamma} \frac{1}{z-a}dz = \oint_{\text{circle}} \frac{1}{z-a}dz = \int_{0}^{2π} \frac{iR e^{it}}{R e^{it}}dt = \int_{0}^{2π} idt = i \cdot 2\pi = 2\pi i$.

Since γ can be continuously shrunk to this circle without crossing the singularity, the integral over γ equals the same value.

2 Solution. Residue viewpoint. The function $f(z) = \frac{1}{z-a}$ has a simple pole at z = a with residue $Res(f, a) = \lim_{z \to a} (z – a)·\frac{1}{z-a} = 1.$

Recall. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$. The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$

A residue is the “fingerprint” of a singularity that tells you how much that singularity contributes to a contour integral.

Cauchy’s residue theorem for a simple closed curve γ enclosing a once (counter-clockwise) gives $\oint_{\gamma} f(z) dz = 2\pi i \sum Res(f, z_k) $ = 2πi × 1 = 2πi.

• Let f(z) = $e^z$. It is entire (analytic everywhere). Therefore, its integral around any simple closed contour is always zero. $\oint e^z dz = 0$.

Path independence in practice. For any two paths $\gamma_1, \gamma_2$ from 1 to 1 + i in $\mathbb{C}, \int_{\gamma_1} e^z dz = \int_{\gamma_2} e^z dz = e^{1+i}-e^1$.

Because $e^z$ is entire, the integral depends only on the endpoints, not on the route taken. The integrand has the global antiderivative F(z) = $e^z$ on $\mathbb{C}$. Hence, for any path γ from 1 to 1+i (the fundamental theorem of calculus in the complex plane), $\int_{\gamma} e^z dz = F(1+i) - F(i) = e^{1+i}-e^1$

• Let R be a rectangular region R = {x + iy: a ≤ x ≤ b, c ≤ y ≤ d}. Let ∂R denote the simple closed contour which is the boundary of R (positively oriented boundary). If f is an analytic function on a open set containing $\bar{R}$, then $\oint_{∂R} f(z)dz = 0.$

• Piecewise smooth polygon. Let γ be any simple, positively-oriented, piecewise-C¹ (it can be broken into finitely many smooth arcs with continuous derivatives, except possibly at finitely many corners) closed curve (triangle, square, any simple polygon or “wildly wiggly”). If f is analytic on and inside γ (γ ∪ Int(γ)), $\oint_{\gamma} f(z)dz = 0.$

The polygonal or “wiggly” nature of $\gamma$ does not matter, because the integral depends only on the analyticity of f and the absence of singularities inside.

The deformation principle lets us locally smooth corners without changing the integral, so even a pure polygon is admissible. No singularities are allowed inside, so the double integral in Green’s formula vanishes by the Cauchy–Riemann equations exactly as before.

Hence, whether γ is a tidy triangle or a fractal-looking simple loop, analyticity on and inside forces the integral to be zero.