Mastering the Cauchy Integral Formula: A Practical Guide

I have yet to see any problem, however complicated, which, when looked at in the right way did not become still more complicated, Paul Anderson.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

• A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
• Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
• Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
• Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

In this definition, we integrate the function f along the path traced out by $\gamma(t)$. The term $\gamma^{'}(t)$ (the derivative of $\gamma$) accounts for the direction and speed of traversal along the path. This definition essentially transforms or converts the complex line integral into a regular real integral over the interval [a, b] via the parametrization $\gamma(t)$. The factor $\gamma'(t)dt = d\gamma$ represents an infinitesimal step along the curve, so $f(\gamma(t))\gamma'(t)dt$ is the infinitesimal contribution to the integral from that step.

Cauchy Integral Formula

Theorem. Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

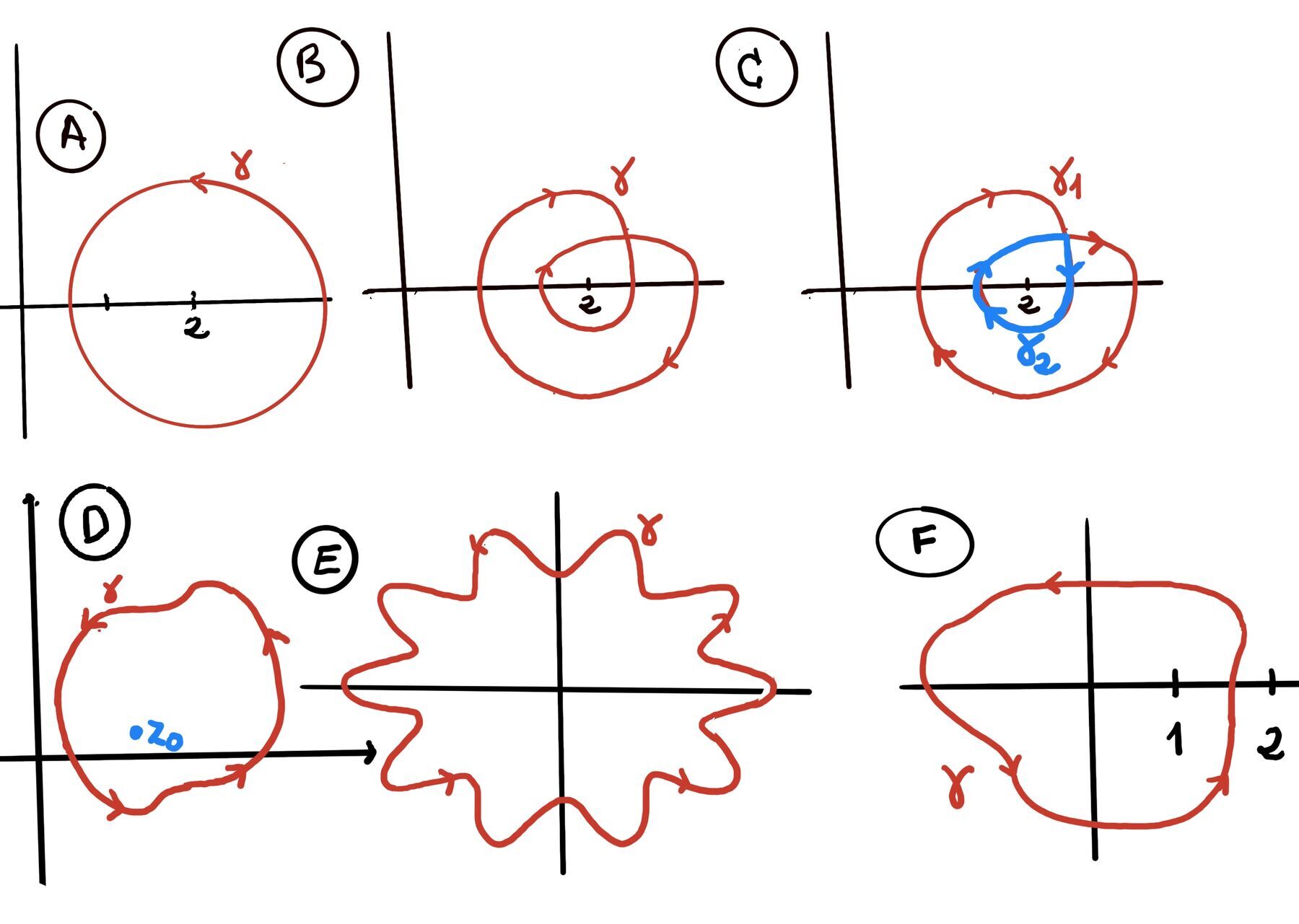
It states that the value of an analytic function at any point z₀ is completely determined by the values the function takes on any simple closed curve that encircles the point. If you know the function’s values on the boundary, you know everything about the function’s behavior inside that boundary. This is quite unlike anything you’ve probably encountered with functions of real variables.

1. A more generalized version is as follows: $f^{(n)}(z_0) = \frac{n!}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz$.

2. Cauchy Integral Formula (Winding Number Lemma). Let γ be a closed rectifiable curve in ℂ, f analytic on an open set containing γ and its interior. For any point a not on γ, the Cauchy Integral Formula states: $\oint_{\gamma} \frac{f(z)}{z-a}dz = 2\pi i \cdot n(\gamma, a) \cdot f(a)$
   The winding number is defined as $n(γ, a) = \frac{1}{2πi}\oint_\gamma \frac{dz}{z-a}$. This represents the net number of times γ winds around a counterclockwise.
   For simple closed curves with positive orientation n(γ, a) = 1 if a is inside γ, 0 if outside.
   For multiple windings n(γ, a) counts the net winding (e.g., 2 for two counterclockwise loops, -1 for one clockwise loop).
   The formula reduces to the basic Cauchy Integral Formula when n(γ, a) = 1.

3. The formula can be used to calculate integrals: $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$

4. Key Conditions:
   Analyticity: $ f(z) $ must be analytic (holomorphic) inside and on $\gamma$.
   Contour $ C $: $\gamma$ is a simple closed curve (e.g., a circle, ellipse). A simple closed curve is a curve that has no self-intersections and is closed, meaning it starts and ends at the same point.
   Point $z_0$: $z_0$ must lie inside $\gamma$. If $z_0$ is outside $\gamma$, the integral is zero.

Cauchy Integral Formula Examples.

• Unit circle. Let γ be the unit circle ∣z∣ = 1 traversed once counterclockwise (positively oriented), and a = 0. $n(\gamma, 0) = \frac{1}{2\pi i}\oint_{|z|=1} \frac{dz}{z} = \frac{1}{2\pi i} \cdot 2\pi i = 1$, the contour is simple, positively oriented, and encloses a = 0 exactly once. For any f analytic on $|z| \leq 1: \oint_{|z|=1} \frac{f(z)}{z}dz = 2\pi i \cdot 1 \cdot f(0) = 2\pi i f(0)$.
• Let γ be a figure-eight curve with one loop enclosing a and the other not. $\gamma = \gamma_{right} + \gamma_{left}$. If a is inside the right loop (traversed counterclockwise): $n(\gamma, a) = 1$. If a is inside the left loop (traversed clockwise): $n(\gamma, a) = -1$. If a is outside both loops: $n(\gamma, a) = 0$.

Thus: $\oint_{\gamma} \frac{f(z)}{z-a}dz = \begin{cases} 2\pi i f(a) & \text{if a in right loop, enclosed positively by } \gamma_{right} \\ -2\pi i f(a) & \text{if a in left loop, enclosed negatively by } \gamma_{left} \\ 0 & \text{if a outside both loops} \end{cases}$

• Let γ be the unit circle |z| = 1 traversed twice counterclockwise, and a = 0, $\gamma(t) = e^{it}, t \in [0, 4\pi]$. Then, $n(\gamma, 0) = \frac{1}{2\pi i}\int_0^{4\pi} \frac{ie^{it}}{e^{it}}dt = \frac{1}{2\pi i} \cdot 4\pi i = 2$, the curve wraps around a = 0 twice in the positive direction. Result: $\oint_{\gamma} \frac{f(z)}{z}dz = 2\pi i \cdot 2 \cdot f(0) = 4\pi i f(0).$

• Point Outside Contour If a is outside γ (e.g., γ is unit circle, |z| = 1, a = 2, a point outside the contour): $n(\gamma, 2) = 0$ since the contour does not enclose the point a = 2, the net number of times it winds around a is zero. Result: For any f(z) analytic on $|z| \leq 2$, the entire integrand $g(z) = \frac{f(z)}{z-2}$ is analytic inside and on the unit circle, then $\oint_{|z|=1} \frac{f(z)}{z-2}dz = 2\pi i \cdot 0 \cdot f(2) = 0$.

Cauchy Integral Form Proof

Note: We will use $a$ for the point inside $\gamma$ and $w$ for the integration variable.

The function being integrated, $g(w) = \frac{f(w)}{w-a}$, has a singularity at w = a, which is inside the contour $\gamma$. Therefore, we cannot apply Cauchy’s Theorem directly.

Since a ∈ inside of γ, there exists an R > 0 such that $\mathcal{B(a; R) \subseteq \mathcal{I(\gamma)}}, \forall r \le R$

$\oint_{\gamma} \frac{f(w)}{w-a}dw =[\text{Cauchy's Theorem for Multiply Connected Domains}] \oint_{\gamma(a; r)} \frac{f(w)}{w-a}dw$ (i) where γ(a; r) is a small circle of radius r centered at a, chosen such that the entire circle and its interior are inside $\gamma$. $\gamma(a; r)$ is parameterized as $\gamma(t) = a + e^{2\pi i\theta}, 0 \le \theta \le 2\pi$.

The Principle of Deformation of Contours states: If f(z) is analytic in a multiply connected region bounded by an outer simple closed contour $\gamma$ and a collection of inner contours $\gamma_1, \gamma_2, \dots, \gamma_n$, then the integral over the outer contour equals the sum of the integrals over the inner contours (all oriented consistently),$\oint_{\gamma} f(z)dz = \sum_{k=1}^n \oint_{\gamma_k} f(z)dz$. In this case: The outer boundary is $\gamma$. The “hole” (the singularity a) is surrounded by the inner boundary $\gamma(a; r)$.

Therefore, the principle directly applies: the integral over the large contour $\gamma$ is equal to the integral over the small contour $\gamma(a; r)$ that encloses the same singularity.

$\oint_{\gamma(a; r)} \frac{f(a)}{w-a}dw =[\text{f(a) is a constant}] f(a)\oint_{\gamma(a; r)} \frac{1}{w-a}dw = f(a)\cdot 2\pi i$. Rearranging this to solve for $f(a)$ gives: $f(a) = \frac{1}{2\pi i}\oint_{\gamma(a; r)} \frac{1}{w-a}dw$ (ii)

$$ \begin{aligned} |\frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{w-a}dw -f(a)| &=[i] |\frac{1}{2\pi i}\oint_{\gamma(a; r)} \frac{f(w)}{w-a}dw -f(a)| \\[2pt] &=[ii, \text{Contour integrals are linear}] |\frac{1}{2\pi i}\oint_{\gamma(a; r)} \frac{f(w)-f(a)}{w-a}dw| \\[2pt] &\le[\text{By the M L Estimation Theorem}, |i| = 1] \frac{1}{2\pi}\oint_{\gamma(a; r)} \frac{|f(w)-f(a)|}{|w -a|}|dw| \\[2pt] &\le \frac{1}{2\pi}\cdot M\oint_{\gamma(a; r)} \frac{1}{|w-a|}|dw| \\[2pt] &= \frac{1}{2\pi}\cdot M\oint_{\gamma(a; r)} \frac{1}{|re^{i\theta}|}|ri e^{i\theta}d\theta| = \frac{1}{2\pi} \cdot M\int_{\theta = 0}^{2\pi} \frac{1}{r}rd\theta = \frac{1}{2\pi} M\int_{\theta = 0}^{2\pi} d\theta = \frac{1}{2\pi} M \cdot 2\pi = M. \end{aligned} $$

where $M = max\{ |f(w)-f(a)|: w = a + re^{i\theta} \}, 0 \le \theta \le 2\pi$

$|\frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{w-a}dw -f(a)| \le M$ (iii)

Since f is analytic in D, it is continuous at a.

The left side (LHS) of the inequality (iii) is constant and does not depend on r. The right side (RHS), M does depend on r. By the definition of continuity, as the radius $r$ shrinks to zero, the points $w = a + re^{i\theta}$ approach a, $\lim_{r \to 0} f(w) = f(a)$. Therefore, the maximum difference $M = \max |f(w) - f(a)|$ must also approach zero: $\lim_{r \to 0} M = 0$

Since the LHS is $\le M$, and M can be made arbitrarily small by choosing $r \to 0$ (arbitrarily small), the LHS must be zero, $|\frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{w-a}dw -f(a)| = 0 \leadsto \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{w-a}dw -f(a) = 0 \leadsto \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{w-a}dw = f(a)$.

Examples

• A Simple Case. Let $\gamma$ be the unit circle $|z| = 1$, and let $f(z) = 1$. Let $z_0 = 0$, the center of the circle. $\oint_\gamma \frac{1}{z - 0} \, dz = \oint_\gamma \frac{1}{z} dz = 2\pi i \cdot f(0) = 2\pi i \cdot 1 = 2\pi i$

• Polynomial Function. Let $f(z) = z^2$ (it is analytic everywhere), $\gamma$ be the circle $ |z| = 2 $, and $z_0 = 1$ (it lies inside the circle ∣z∣ = 2), $\oint_\gamma \frac{z^2}{z - 1} dz =[\text{ Cauchy Integral Formula }] 2\pi i \cdot f(1) = 2\pi i (1^2) = 2\pi i$

Here, even though $f(z)/(z - 1) $ has a singularity at $z = 1$, the contour $\gamma$ encloses the point $z_0 = 1$, so the formula applies.

• Evaluate $\oint_{\gamma(2; 3)} \frac{z + 1}{z - 2} dz$ where $\gamma(2; 3)$ is a circle of radius 3 centered at 2 orientated in the positive (traversed counterclockwise) direction.

Let f(z) = z + 1, f is entire, i.e., analytic everywhere because polynomials are entire functions.

$\oint_{\gamma(2; 3)} \frac{z + 1}{z - 2} dz = \oint_{\gamma(2; 3)} \frac{f(z)}{z - 2} dz =[\text{ Cauchy Integral Formula }, 2 \in \mathcal{I}(\gamma(2; 3))] 2\pi i \cdot f(2) = 2\pi i \cdot 3 = 6\pi i$

• Compute $\oint_\gamma \frac{e^{2z}}{z - 2} dz$ where the contour is the circle of radius 2 centered at the origin (|z| = 2), the point $z_0 = 1$ lies inside the circle (|1| < 2), the function f(z) = $e^{2z}$ is analytic everywhere, and n (order) = 0.

$\oint_\gamma \frac{e^{2z}}{z - 2} dz = 2\pi i \cdot f(1) = 2\pi i \cdot e^{2\cdot 1} = 2\pi ie^2$

• Point Outside the Contour. Let f(z) = 1, $\gamma$ be the unit circle |z| = 1, and $z_0 = 2$ (outside $\gamma$). $\oint_\gamma \frac{1}{z - 2} dz = 0$.

The integrand has a singularity at $z_0 = 2$ (it lies outside the unit circle), but is analytic on and inside the contour $\gamma$, so the integral vanishes (Cauchy’s Theorem).

• Evaluate $\oint_{\gamma} \frac{\cos(z)}{z^2+1}dz$ where γ is a simple and smooth closed curve orientated in the positive orientation (traversed counterclockwise) lying in the upper half plane, hence containing i in the inside of γ.

$$ \begin{aligned} \oint_{\gamma} \frac{\cos(z)}{z^2+1}dz = &=\oint_{\gamma} \frac{\cos(z)}{(z-i)(z+i)}dz \\[2pt] &=\oint_{\gamma} \frac{\frac{\cos(z)}{z+i}}{z-i}dz \\[2pt] &[f(z) = \frac{\cos(z)}{z+i} \text{is analytic on an open set containing } \gamma^* \cup \mathcal{I}(\gamma)] \\[2pt] &=[\text{By Cauchy's Integral Formula}] 2\pi i\cdot f(i) = 2\pi i \frac{cos(i)}{2i} \\[2pt] &= \pi cos(i) = \pi (\frac{e^{i(i)}+e^{-i(i)}}{2}) = \pi (\frac{e^{-1}+e^{1}}{2}) = \frac{\pi (e^2 + 1)}{2e} \end{aligned} $$

• The Generalized Formula (n > 0). Compute $\oint_\gamma \frac{sin(z)}{(z-\frac{\pi}{2})^3} dz$ where the contour is the circle of radius 2 centered at the origin (|z| = 2), the point $z_0 = \frac{\pi}{2}$ lies inside the circle ($|\frac{\pi}{2}| \approx 1.57 < 2$), the function f(z) = $sin(z)$ is analytic everywhere (f′(z) = cos(z), f′′(z) = −sin(z)), and n (order) = 2 (n + 1 = 3).

$\oint_\gamma \frac{sin(z)}{(z-\frac{\pi}{2})^3} dz = \frac{2\pi i}{2!}f^{''}(\frac{\pi}{2}) = \frac{2\pi i}{2!} \cdot (-sin(\frac{\pi}{2})) = \pi i \cdot (-1) = -\pi i.$

• Let $f(z) = e^z$, $z_0 = 0$, and $\gamma$ be the unit circle |z| = 1. $\oint_C \frac{e^z}{z^2} dz =[\text{Generalized formula, n = 1}] \frac{2\pi i}{1!} f'(0) = 2\pi i \cdot e^0 = 2\pi i$

• Compute $\oint_\gamma \frac{e^{z^2}}{z-2}dz$ where $\gamma$ is the curve shown in Figure A. Since f(z) = $e^{z^2}$ is entire, $\gamma$ is a simple closed curve (counterclockwise), and z = 2 lies inside $\gamma, \oint_\gamma \frac{e^{z^2}}{z-2}dz = 2\pi i f(2) = 2\pi i e^4$.

• Compute $\oint_\gamma \frac{cos(z)}{z-1}dz$ where $\gamma$ is the curve shown in Figure F. f(z) = $cos(z)$ is entire, $\gamma$ is a positively oriented simple closed curve, and z = 1 lies inside $\gamma$, $\oint_\gamma \frac{cos(z)}{z-1}dz = 2\pi i \cdot f(1) = 2\pi i \cdot cos(1) \approx 1.08\pi i$.

• Compute $\oint_\gamma \frac{cos(z)}{3z-1}dz$ where $\gamma$ is the curve shown in Figure F. f(z) = $cos(z)$ is entire, $\gamma$ is a positively oriented simple closed curve, and z = 1/3 lies inside $\gamma$, $\oint_\gamma \frac{cos(z)}{3z-1}dz = \oint_\gamma \frac{cos(z)}{3(z-\frac{1}{3})}dz = \frac{1}{3}\oint_\gamma \frac{cos(z)}{z-\frac{1}{3}}dz = \frac{2\pi i}{3} \cdot f(\frac{1}{3}) = \frac{2\pi i}{3} \cdot cos(\frac{1}{3}) \approx 0.63\pi i$.

• Compute $\oint_\gamma \frac{cos(z)}{(z-1)(z-2)}dz$ where $\gamma$ is the curve shown in Figure F. f(z) = $\frac{cos(z)}{z-2}$ is analytic inside $\gamma$, $\gamma$ is a positively oriented simple closed curve, and z = 1 lies inside $\gamma$ (it encloses z = 1, but not z = 2), $\oint_\gamma \frac{cos(z)}{(z-1)(z-2)}dz = \oint_\gamma \frac{\frac{cos(z)}{z-2}}{(z-1)}dz = 2\pi i \cdot \frac{cos(1)}{(1-2)} = 2\pi i \cdot -cos(1) \approx -1.08\pi i$.

• Compute $\oint_\gamma \frac{2z^2-1}{(z-1)^2}dz$ where $\gamma$ is the curve shown in Figure F. f(z) = $2z^2-1$ is analytic on and inside $\gamma$, $\gamma$ is a positively oriented simple closed curve, and z = 1 lies inside $\gamma$, $\oint_\gamma \frac{2z^2-1}{(z-1)^2}dz =[\text{Generalized formula, n = 1}] \frac{2\pi i}{1!} \cdot f'(1) = 2\pi i \cdot 4 \cdot 1 = 8\pi i$.

• Compute $\oint_\gamma \frac{e^{z^2}}{z-2}dz$ where $\gamma$ is the curve shown in Figure B. f(z) = $e^{z^2}$ is entire, $\gamma$ goes around 2 twice in the clockwise direction, so we break $\gamma$ into $\gamma_1$ and $\gamma_2$ as shown in Figure C.

$\oint_\gamma \frac{e^{z^2}}{z-2}dz = \oint_{\gamma_1} \frac{e^{z^2}}{z-2}dz + \oint_{\gamma_2} \frac{e^{z^2}}{z-2}dz = -2\pi i f(2) -2\pi i f(2) = -4\pi i e^4$.

The negative signs are because they go clockwise around $z_0$ = 2.

• Compute $\oint_{\gamma(0; 2)} \frac{1}{z^2+z+1}dz$, our contour is the circle centered at the origin with radius 2, |z| = 2. The integrand is not analytic inside it and we cannot calculate it directly using Cauchy Integral Formula.

The singularities occur where the denominator is zero: $z^2 + z + 1 = 0$. Using the quadratic formula: $z = \frac{-1 \plusmn \sqrt{(-1)^2 - 4}}{2} = \frac{-1 \plusmn \sqrt{3}i}{2}$. Let the singularities be $\alpha$ and $\beta, \alpha = -\frac{1}{2} + i\frac{\sqrt{3}}{2} = e^{i 2\pi/3}, \beta = -\frac{1}{2} - i\frac{\sqrt{3}}{2} = e^{-i 2\pi/3}$.

The magnitude of both singularities is: $|\alpha| = |\beta| = \sqrt{\left(-\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2} = \sqrt{\frac{1}{4} + \frac{3}{4}} = 1$. Since the contour has radius R = 2, and 1 < 2, both singularities $\alpha$ and $\beta$ lie inside the contour $\gamma(0; 2)$.

We decompose the integrand using partial fractions. $\frac{1}{z^2+z+1} = \frac{A}{z-\alpha} + \frac{B}{z-\beta}$. We find A and B: $1 = A(z-\beta) + B(z-\alpha)$.

Set $z = \alpha$: $1 = A(\alpha - \beta) \implies A = \frac{1}{\alpha - \beta}$

Set $z = \beta$: $1 = B(\beta - \alpha) \implies B = \frac{1}{\beta - \alpha} = -\frac{1}{\alpha - \beta}$

Substituting $A$ and $B$ back and using the linearity of contour integrals, $\oint_{\gamma(0; 2)} \frac{1}{z^2+z+1}dz = \oint_{\gamma(0; 2)} \frac{1}{\alpha - \beta [\frac{1}{z-\alpha} - \frac{1}{z-\beta}]dz} = \frac{1}{\alpha - \beta} [\oint_{\gamma(0; 2)}\frac{1}{z-\alpha} - \oint_{\gamma(0; 2)}\frac{1}{z-\beta}]$

Now, we apply the Cauchy Integral Formula (or Winding Number Lemma) to each integral. The general form of the CIF is $\oint_{\gamma} \frac{f(z)}{z-a}dz = 2\pi i \cdot n(\gamma, a) \cdot f(a)$.

Here, in both integrals, the numerator is simply $f(z) = 1$. The contour $\gamma(0; 2)$ is a simple closed curve, positively oriented, and encloses both $\alpha$ and $\beta$. Thus, the winding numbers are $n(\gamma, \alpha) = 1$ and $n(\gamma, \beta) = 1$ respectively.

= $\frac{1}{\alpha - \beta}[2\pi i\cdot n(\gamma, \alpha)\cdot f(\alpha) - 2\pi i\cdot n(\gamma, \beta)\cdot f(\beta)] = \frac{1}{\alpha - \beta}[2\pi i\cdot 1 \cdot 1 - 2\pi i\cdot 1 \cdot 1] = 0$.

• Compute $\oint_\gamma \frac{e^{2z}}{z^4}dz$ where $\gamma$ is the curve shown in Figure E. Since f(z) = $e^{2z}$ is entire, $\gamma$ is a simple closed curve (counterclockwise), and z = 0 lies inside $\gamma, \oint_\gamma \frac{e^{2z}}{z^4}dz = \oint_\gamma \frac{e^{2z}}{(z-0)^4}dz =[\text{Generalized formula, n = 3}] \frac{2\pi i}{3!}f^{'''}(0) = \frac{2\pi i}{3!} \cdot 8e^0 = \frac{8\pi i}{3}$.