Cauchy's Integral Formula for the First Derivative

Enjoy the little things, for one day you may look back and realize they were the big things, Robert Brault

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

• A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
• Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
• Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
• Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

In this definition, we integrate the function f along the path traced out by $\gamma(t)$. The term $\gamma^{'}(t)$ (the derivative of $\gamma$) accounts for the direction and speed of traversal along the path. This definition essentially transforms or converts the complex line integral into a regular real integral over the interval [a, b] via the parametrization $\gamma(t)$. The factor $\gamma'(t)dt = d\gamma$ represents an infinitesimal step along the curve, so $f(\gamma(t))\gamma'(t)dt$ is the infinitesimal contribution to the integral from that step.

Cauchy Integral Formula

Theorem. Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

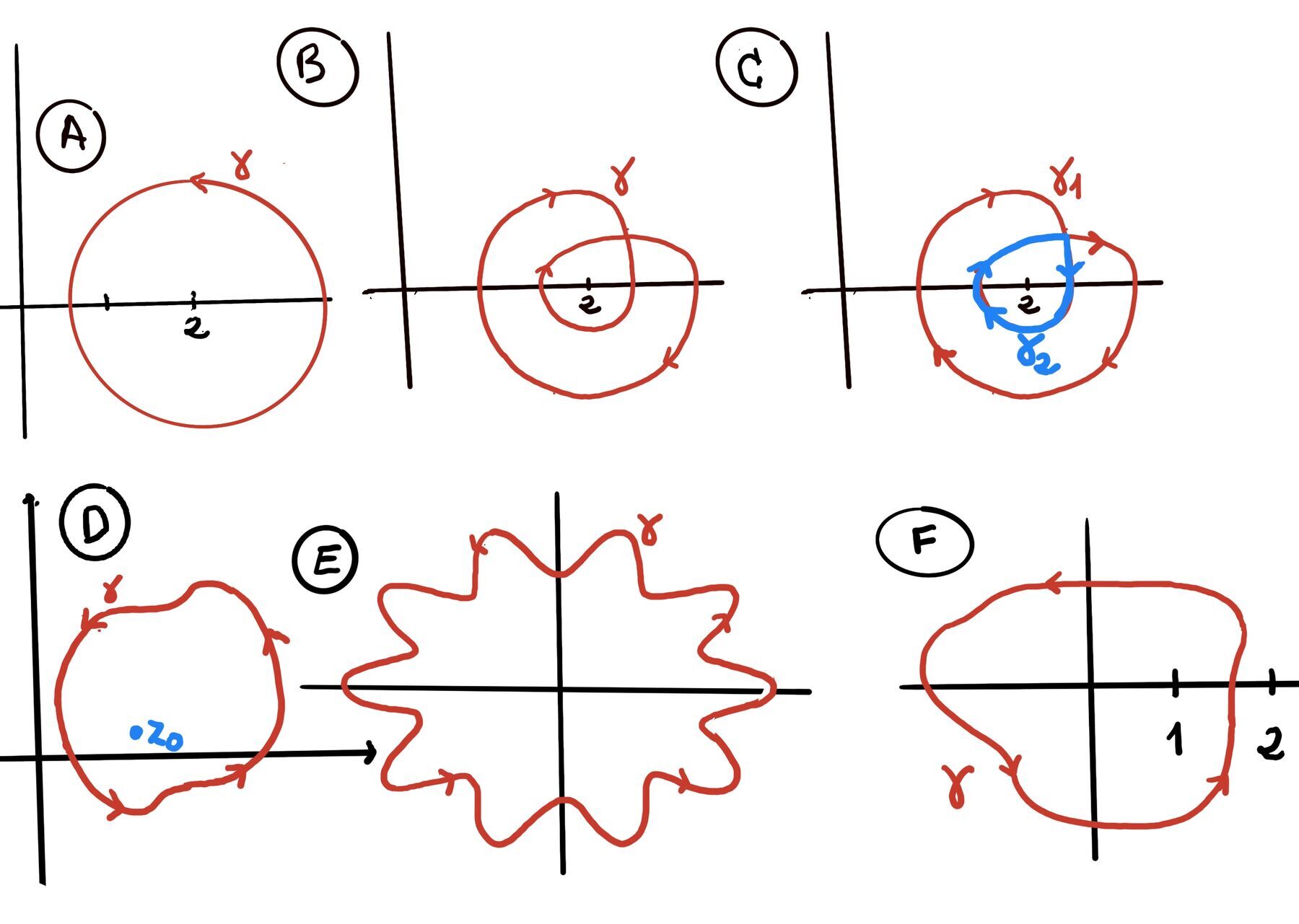
It states that the value of an analytic function at any point z₀ is completely determined by the values the function takes on any simple closed curve that encircles the point. If you know the function’s values on the boundary, you know everything about the function’s behavior inside that boundary. This is quite unlike anything you’ve probably encountered with functions of real variables.

1. A more generalized version is as follows: $f^{(n)}(z_0) = \frac{n!}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz$.

2. Cauchy Integral Formula (Winding Number Lemma). Let γ be a closed rectifiable curve in ℂ, f analytic on an open set containing γ and its interior. For any point a not on γ, the Cauchy Integral Formula states: $\oint_{\gamma} \frac{f(z)}{z-a}dz = 2\pi i \cdot n(\gamma, a) \cdot f(a)$
   The winding number is defined as $n(γ, a) = \frac{1}{2πi}\oint_\gamma \frac{dz}{z-a}$. This represents the net number of times γ winds around a counterclockwise.
   For simple closed curves with positive orientation n(γ, a) = 1 if a is inside γ, 0 if outside.
   For multiple windings n(γ, a) counts the net winding (e.g., 2 for two counterclockwise loops, -1 for one clockwise loop).
   The formula reduces to the basic Cauchy Integral Formula when n(γ, a) = 1.

3. The formula can be used to calculate integrals: $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$

4. Key Conditions:
   Analyticity: $ f(z) $ must be analytic (holomorphic) inside and on $\gamma$.
   Contour $ C $: $\gamma$ is a simple closed curve (e.g., a circle, ellipse). A simple closed curve is a curve that has no self-intersections and is closed, meaning it starts and ends at the same point.
   Point $z_0$: $z_0$ must lie inside $\gamma$. If $z_0$ is outside $\gamma$, the integral is zero.

Cauchy’s Integral Formula for the First Derivative

Cauchy’s Integral Formula for the First Derivative. Let f be analytic on and inside a positively orientated simple closed curve $\gamma$. For any point a inside $\gamma, a \in \mathcal{Int}(\gamma)$, the first derivative f'(a) exists and is given by: $f^{'}(a) = \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{(w-a)^2}dw$.

Proof.

Let $a \in \mathcal{Int}(\gamma)$ be an arbitrary element in the interior of $\gamma$.

By the Principle of Deformation of Contours, the integral over $\gamma$ is equal to the integral over any small, positively oriented circle $\gamma_r$ centered at a, provided $\gamma_r$ lies entirely inside $\gamma$, $\gamma(a; r) \text{ and } Int(\gamma(a; r)) \subset Int(\gamma)$. Let $\gamma(a; 2r)$ be a circle of radius 2r (it simplifies the subsequent steps) centered at a: $\gamma(a; 2r) = \{w : |w-a|=2r\}$. We choose a small r such that $\gamma(a; 2r)$ is inside $\gamma$.

We apply the Cauchy Integral Formula, $f(z) = \frac{1}{2\pi i}\oint_{\gamma_r} \frac{f(w)}{w-z}dw$, to the points a + h and a. We choose h small enough such that a + h also lies inside $\gamma_r$. Specifically, let |h| < r.

$$ \begin{aligned} \frac{f(a+h) - f(a)}{h} &=\frac{1}{h} \left[ \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{w-(a+h)}dw - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{w-a}dw \right] \\[2pt] &\text{Using the linearity property of contour integrals, we combine the terms:} \\[2pt] &=\frac{1}{2\pi i h}\oint_{\gamma(a; 2r)}[\frac{f(w)}{w-a-h}-\frac{f(w)}{w-a}]dw \\[2pt] &\text{Combine the fractions inside the integral using a common denominator:} \\[2pt] &\frac{1}{w-a-h} - \frac{1}{w-a} = \frac{(w-a) - (w-a-h)}{(w-a-h)(w-a)} = \frac{h}{(w-a-h)(w-a)} \\[2pt] &=\frac{1}{2\pi i h}\oint_{\gamma(a; 2r)} \frac{f(w) \cdot h}{(w-a-h)(w-a)}dw \\[2pt] &\text{The factor $h$ cancels out:} \\[2pt] &=\frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a-h)(w-a)}dw \\[2pt] \end{aligned} $$

Thus, $\frac{f(a+h) - f(a)}{h} = \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a-h)(w-a)} dw \text{ (i)}$

We are trying to prove that the limit of the difference quotient equals the proposed integral $\frac{1}{2\pi i}\oint \frac{f(w)}{(w-a)^2}dw$. We examine the error term:

$$ \begin{aligned} Error &= \frac{f(a + h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw \\[2pt] &\text{Substitute the expression from (i) and combine the integrals:} \\[2pt] &=\frac{1}{2\pi i} \oint_{\gamma(a; 2r)} f(w)[\frac{1}{(w-a-h)(w-a)}-\frac{1}{(w-a)^2}]dw \\[2pt] &\text{Combine the fractions inside the brackets using the common denominator} \\[2pt] &\frac{(w-a) - (w-a-h)}{(w-a-h)(w-a)^2} = \frac{h}{(w-a-h)(w-a)^2} \\[2pt] &= \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w) \cdot h}{(w-a-h)(w-a)^2} dw \\[2pt] &\text{The error term simplifies to:} \\[2pt] &= \frac{h}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a-h)(w-a)^2} dw \end{aligned} $$

We must show that $\lim_{h \to 0} |\text{Error}| = 0$.

Bounding the Error with M L-Estimation:

1. Contour Length L: The length of the contour $\gamma(a; 2r)$ is $L = 2\pi (2r) = 4\pi r$.
2. Bound for |f(w)|: Since f is analytic, it is continuous on the compact contour $\gamma(a; 2r)$. Thus, f is bounded: $|f(w)| \le M$ for some M, $M = \max_{w \in \gamma(a; 2r)} |f(w)|$.

   If a function $f(z)$ is analytic (complex differentiable) at a point, it is automatically continuous at that point. Since f is analytic in a domain containing the contour $\gamma(a; 2r)$, it must be continuous on that contour. A set in $\mathbb{C}$ is compact if it is closed (contains its boundary) and bounded (can be enclosed by a finite circle). The circle $\gamma(a; 2r)$, defined by |w - a| = 2r, is a closed and bounded set, making it a compact set. The Extreme Value Theorem (Weierstrass Theorem) states that a continuous function defined on a compact set must attain both its maximum and minimum values on that set. Since f(w) is continuous on the compact set $\gamma(a; 2r)$, the maximum value of the magnitude, |f(w)|, must exist and be finite.

3. Bound for |w - a|: For w on the circle $\gamma(a; 2r), w \in \gamma(a; 2r)^*$, the distance is exactly |w - a| = 2r.
4. Bound for |w -a -h|: We chose |h| < r. By the Reverse Triangle Inequality: $|w-a-h| \ge ||w-a| - |h|| = |2r - |h||$. Since |h| < r, then $-|h| > -r \leadsto 2r - |h| > 2r - r = r > 0, |w-a-h| \gt r$.

$$ \begin{aligned} |Error| &=|\frac{f(a + h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw| \\[2pt] &=|\frac{h}{2\pi i} \oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a-h)(w-a)^2} dw| \\[2pt] &\text{By the ML-Estimation Theorem} \\[2pt] &=\frac{|h|}{2\pi} \oint_{\gamma(a; 2r)} \frac{|f(w)|}{|w-a-h||w-a|^2}|dw| \\[2pt] &\text{Substitute all bounds:} \\[2pt] &\le \frac{|h|}{2\pi} \cdot \frac{M}{(r) (2r)^2} \cdot (4\pi r) \\[2pt] &\text{Simplify the expression:} \\[2pt] &= \frac{|h|}{2\pi} \cdot \frac{M}{4r^3} \cdot (4\pi r) = \frac{|h| M (4\pi r)}{8\pi r^3} = \frac{|h| M}{2r^2} \end{aligned} $$

The inequality is: $|Error| = \left| \frac{f(a+h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw \right| \le \frac{M}{2r^2} |h|$

As we take the limit $h \to 0, \lim_{h \to 0} \left( \frac{M}{2r^2} |h| \right) = 0$. Since the error term is bounded by a quantity that tends to zero, the error term itself must tend to zero: $\lim_{h \to 0} |\frac{f(a + h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw| = 0 \leadsto \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw = 0$

Last step. We established the key inequality:

$$0 \le \left| \underbrace{\frac{f(a+h) - f(a)}{h} - \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw}_{\text{Error Term } E(h)} \right| \le \underbrace{\frac{M}{2r^2} |h|}_{\text{Upper Bound } B(h)}$$

The Squeeze Theorem: Since $|E(h)|$ is squeezed between two functions whose limits are both 0, the limit of $|E(h)|$ must also be 0

Since $- \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw$ is constant related to h, the derivative exists, and its value is $f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} = \frac{1}{2\pi i}\oint_{\gamma(a; 2r)} \frac{f(w)}{(w-a)^2}dw$

Finally, by the Deformation of Contours, the integral over the small circle $\gamma(a; 2r)$ is equal to the integral over the original contour $\gamma: f'(a) = \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{(w-a)^2}dw$

We normally write it as $f'(z) = \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{(w-z)^2}dw, z \in I(\gamma)$