Cauchy-Goursat theorem

Without pain, without sacrifice, we would have nothing, Fight Club.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

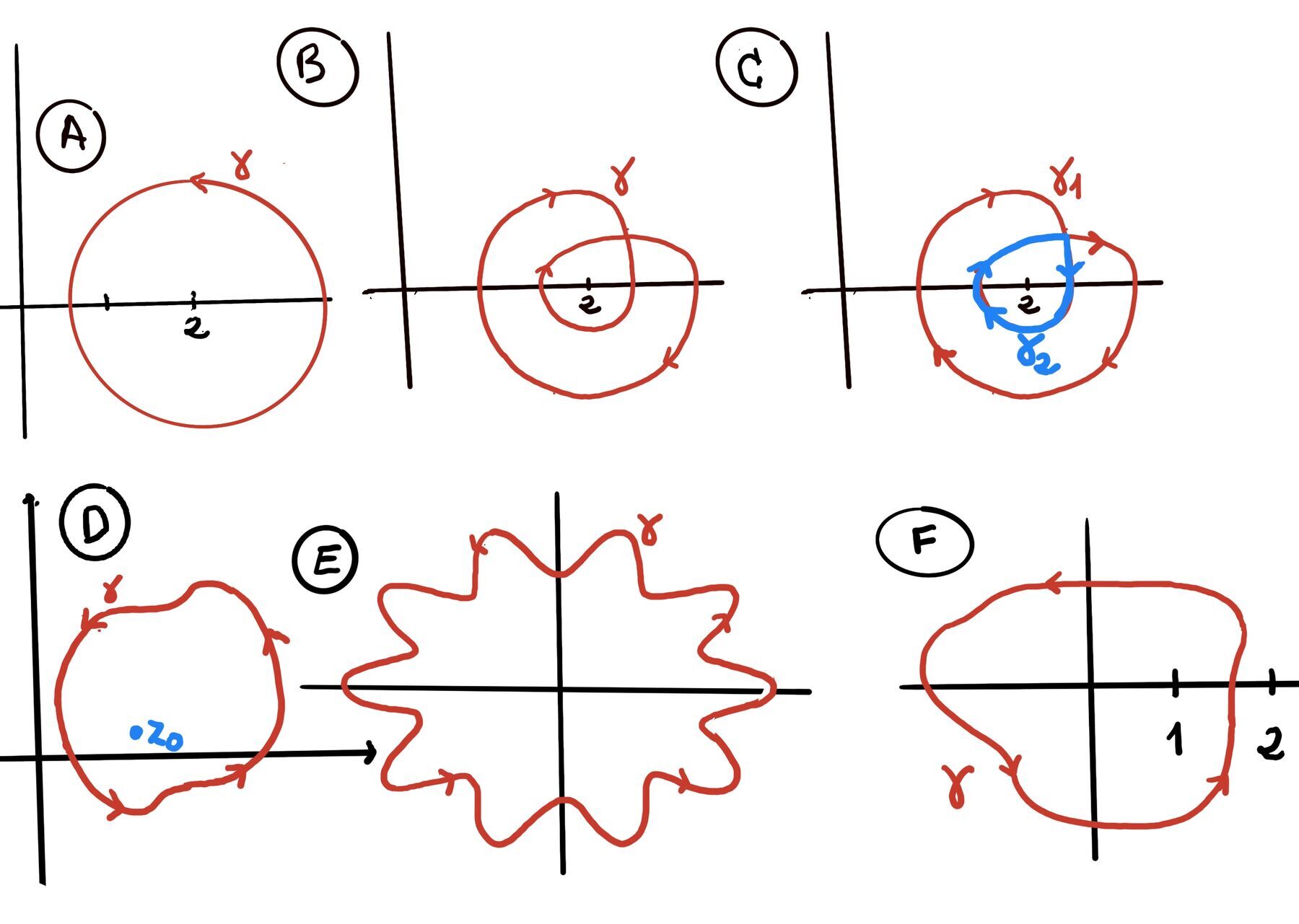
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

• Cauchy’s Theorem for a Rectangle. Let R be a rectangle region R = {x + iy: a ≤ x ≤ b, c ≤ y ≤ d}. Let f be analytic on an open set that contains R (so f is analytic on and in a neighborhood of R). Then, the positively oriented boundary (∂R) contour integral of f vanishes, $\int_{\partial R}f(z)dz = 0$.

Similarly, Let T be a triangular region. Let f be analytic on an open set that contains T (so f is analytic on and in a neighborhood of T). Then, the positively oriented boundary (∂T) contour integral of f vanishes, $\int_{\partial T}f(z)dz = 0$.

• Once we believe the rectangle case, we get every simple polygon for free by a tiling or triangulation argument. In other words, $\int_{\partial C}f(z)dz = 0$ for any positively oriented simple polygon C (non-self-intersecting, closed) when f is analytic on an open set that contains C (so f is analytic on and in a neighborhood of C) (Figure 5).

There are several forms of Cauchy’s theorem. If C is a closed polygonal contour lying entirely within a simply connected domain D, f is a complex function analytic in D, then $\int_{\partial C}f(z)dz = 0$.

• Cauchy’s Theorem for Rectifiable (the curve can be approximated by polygons whose lengths converge its length) Jordan Curves (simple, closed, and of a finite length) Jordan curves . Let Γ be a rectifiable Jordan curve and let f be analytic on an open set Ω containing Γ ∪ Int(Γ). Then, $\oint_{\Gamma} f(z)dz = 0.$

• Cauchy–Goursat theorem. Let γ be a simple closed contour (piecewise smooth, rectifiable Jordan curve) and let f be analytic on an open set Ω containing γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$. Then, $\oint_{\gamma} f(z)dz = 0$..

Proof.

Proof 1. A simple closed contour γ is a rectifiable Jordan curve (since it’s piecewise smooth and has finite length). The earlier theorem states: If f is analytic on an open set containing a rectifiable Jordan curve Γ and its interior, then $\oint_{\Gamma} f(z)dz = 0.$

Since γ is a rectifiable Jordan curve and f is analytic on an open set containing γ ∪ Int(γ), the conditions are satisfied. Therefore, $\oint_γ f(z)dz = 0.$

Proof 2. The core idea of this proof is to show that a “complicated” integral over a smooth, curvy path $\gamma$ can be replaced by a “simple” integral over a polygon $P$ without changing the value.

Consider a simple closed contour γ and choose n points $z_1, z_2, \cdots z_n$ on γ arranged in positive orientation. Construct a simple polygon P by connecting consecutive points with straight line segments. Ensure the partition is sufficiently fine so that:

1. The arc length between consecutive points is small.
2. The polygon P remains simple (no self-intersections).
3. P lies entirely within Ω (possible since Ω is open and contains a neighborhood of γ).

We compare the integrals along γ and P (The total integral is just the sum of the integrals over these small pieces): $|\oint_γ f(z)dz - \oint_P f(z)dz| \le |\sum_{i=1}^n |\oint_{γ_i} f(z)dz - \oint_{P_i} f(z)dz|$ where γᵢ is the small arc from zᵢ to zᵢ₊₁ and Pᵢ is the straight chord (a line segment) from zᵢ to zᵢ₊₁.

Our new, simpler goal is to show that the difference on just one small piece, $\left| \int_{\gamma_i} f(z)dz - \int_{P_i} f(z)dz \right|$, is extremely small.

Parameterize γᵢ by z(t) and Pᵢ by w(t) = zᵢ + t(zᵢ₊₁ - zᵢ) for t ∈ [0,1]. Since f is analytic on Ω which means it is continuous on the compact (closed and bounded) set containing $\gamma$ and its interior, it is uniformly continuous. For any ε > 0, choose δ such that |f(z) - f(w)| < ε when |z - w| < δ. This is a powerful tool. It means we can “tame” the function $f(z)$ over the entire curve at once. Refine the partition so that every single arc length Lᵢ < δ and chord length |zᵢ₊₁ - zᵢ| < δ.

For each segment: $|\oint_{γ_i} f(z)dz - \oint_{P_i} f(z)dz| = |\int_0^1 [f(z(t))z^′(t)−f(w(t))(z_{i+1}−z_i )]dt|$

Add and subtract $f(z(t))(z_{i+1}-z_i), $

$= |\int_0^1 f(z(t))[z^′(t) - (z_{i+1}-z_i)dt] + \int_0^1 [f(z(t)) −f(w(t))](z_{i+1}−z_i )dt|$

First term.

$|\int_0^1 f(z(t))[z^′(t) - (z_{i+1}-z_i)dt] =[\text{ Since } \int_0^1 z^′(t)dt = z_{i+1} - zᵢ] |\int_0^1 [f(z(t)) - f(z_i)] [z^′(t) - (z_{i+1}-z_i)]dt|$

Let Mᵢ = max|f(z(t)) - f(zᵢ)|. Then: First term ≤ $M_i(\int_0^1 |z^′(t)|dt + |z_{i+1}-z_i|dt) ≤ M_i(L_i + L_i)= 2M_i L_i$

z(t) traces the arc γᵢ from zᵢ to zᵢ₊₁. Mᵢ measures how much f deviates from its value at the starting point along the entire arc. Why this maximum exist? The arc γᵢ is compact (closed and bounded). f is continuous (since analytic). A continuous function on a compact set attains its maximum

Second term: $|\int_0^1 [f(z(t)) −f(w(t))](z_{i+1}−z_i )dt| \le N_i|z_{i+1}-z_i| \le N_iL_i$ where Nᵢ = max|f(z(t)) - f(w(t))|

z(t) is on the arc γᵢ. w(t) is on the chord Pᵢ (straight line segment). Both are parameterized by the same t ∈ [0, 1]. Nᵢ measures the maximum difference between f on the arc and f on the chord. Why this maximum exists: The set {(z(t), w(t)) : t ∈ [0,1]} is compact. The function (z, w) ↦ |f(z) - f(w)| is continuous. Therefore, the maximum is attain. Intuitively, the arc and chord are very close (both within the $\delta$-neighborhood), therefore $z(t)$ and $w(t)$ are closer than $\delta$. By uniform continuity, $N_i = \max|f(z(t)) - f(w(t))| < \epsilon$.

f is analytic on Ω, hence continuous. The set γ ∪ Int(γ) is compact. A continuous function on a compact set is uniformly continuous. Therefore, ∀ε > 0, ∃δ > 0 such that: ∣z − w∣ < δ ⇒ ∣f(z) − f(w)∣ < ε.

For sufficiently fine partition: The entire arc γᵢ lies within a δ-ball around zᵢ ⇒ Mᵢ < ε. The distance between z(t) and w(t) < δ for all t ⇒ Nᵢ < ε.

$|\text{Difference}_i| \le |\text{Term 1}| + |\text{Term 2}| < 2\epsilon L_i + \epsilon L_i = 3\epsilon L_i$ So, for each piece i, the error is bounded by $3\epsilon$ times its length.

Thus, each segment difference < 3εLᵢ. Summing over all segments: $|\oint_γ f(z)dz - \oint_P f(z)dz| \le \sum_{i=1}^{n} |\text{Difference}_i| \lt [\text{ Now, substitute the bound we just found for each piece: }] \sum_{i=1}^{n} (3\epsilon L_i)$

$=[\text{We can pull the constant $3\epsilon$ out of the sum } ] 3\varepsilon \sum_{i=1}^{n} L_i = 3\varepsilon L$. We have shown that the difference between the curve integral and the polygon integral is less than $3\epsilon L$. Since L is a fixed number (the length of the curve) and ε is arbitrary (we can make the difference smaller than any positive number), the difference approaches 0 as the partition refines n → ∞.

Note: What is $\sum L_i$? It’s the sum of all the little arc lengths, which is just the total length of the original curve $\gamma$, L.

Polygonal Cauchy Theorem. For any simple polygon P, if f is analytic on P ∪ Int(P), then $\oint_P f(z)dz = 0$. By the approximation, $\oint_γ f(z)dz = lim_{n \to \infty} \oint_{P_n} f(z)dz = \lim_{n \to \infty} 0 = 0.$

Then it can be shown that the difference $|\oint_{\Gamma} f(z)dz -\oint_P f(z)dz|$ can be made arbitrarily small as n. Thus, by the previous result, $\oint_P f(z)dz = 0$ for any n. Therefore, $\oint_{\Gamma} f(z)dz = 0.$

Examples Cauchy-Goursat theorem

• Basic Integral Over a Circle. Consider f(z) = $z^2$, and let C be the circle centered at the origin with radius 1. Since f(z) is entire (holomorphic everywhere), we can apply the Cauchy-Goursat theorem: $\oint_C z^2 dz = 0$.
• Counterexample 1. Let $f(z) = \frac{1}{z}$, and let C be the unit circle centered at the origin. Here, f(z) is not defined at z = 0, which lies inside C. Thus, the Cauchy-Goursat theorem does not apply directly because the function is not analytic on the entire region enclosed by C. Instead, we use other techniques such as the residue theorem to evaluate: $\oint_C \frac{1}{z} dz = 2\pi i \neq 0$
• Counterexample 2. Let D be the annulus D = {1 < ∣z∣ < 2} and let C be the circle C: |z| = 1.5. If $f(z) = \frac{1}{z}$, then D is multiply connected (it has a hole at z = 0, any loop around the origin, like |z| = 1.5, cannot be contracted to a point without leaving the domain — because the origin is missing), and the integral: $\oint_{|z|=1.5} \frac{1}{z} \, dz = 2\pi i \neq 0$. This shows it shows you must have analyticity on and inside the specific loop.
• Polygonal/Jordan curves with analytic f: zero integral. Let $\gamma$ be any rectifiable Jordan curve (e.g., a square with vertices (0, 1, 1+i, i, CCW) or a smooth “wobbly” circle) and f analytic on a neighborhood of $\gamma^*\cup Int(\gamma)$ (e.g., f(z) = $z², sin(z), cos(z)$, etc.) Then, $\oint_{\gamma} f(z)dz = 0$. In particular, for f(z) = sin(z): $\oint_\gamma \sin (z)dz=0.$
• Circle where f is analytic and no singularity is encircled: zero integral. Let $f(z)=\dfrac{1}{z-3}$ and C: |z| = 1.5, a circle of radius 1.5 centered at the origin. The interior $|z| \le 1.5$ does not contain z = 3 (the point lies outside the circle). f is analytic on and inside C, so $\oint_{|z|=1.5}\frac{dz}{z-3}=0.$
• Circle where the loop encircles the singularity. Let $f(z) = \frac{1}{z}$ and consider two loops: $C_1$: the circle |z-2| = 0.4. Interior does not contain 0 $\Rightarrow \oint_{C_1} \frac{dz}{z}=0$. $C_2$: the circle $|z| =1.5$. Interior does contain 0 $\Rightarrow \oint_{C_2}\frac{dz}{z}=2\pi i$. Both loops lie inside the same multiply connected domain $D=\mathbb{C}\setminus{0}$, which is not simply connected. The decisive criterion is whether the loop’s interior hits the singularity.
• Removable singularity. Let $f(z)=\dfrac{\sin(z)}{z}$ and C, the unit circle. Although f is undefined at z = 0 , the limit $\lim_{z \to 0} \dfrac{\sin(z)}{z} = 1$ exists and is finite; so by Riemann’s Theorem on Removable Singularities the singularity at z = 0 is removable. Define the “Repaired” Function $g(z)= \begin{cases} \dfrac{\sin(z)}{z}, & z\neq 0, \\\\ 1, & z=0, \end{cases}$, then g is entire (the singularity is removable). Therefore, $\oint_{|z|=1} \dfrac{\sin(z)}{z}dz =[\text{f(z) and g(z) are identical at every point on the contour C}] \oint_{|z|=1} g(z)dz =[\text{Cauchy-Goursat}] 0.$
• Equality of integrals on concentric circles. Let f be analytic on the closed annulus A = { $r_1\le |z| \le r_2 $} (an annulus with no singularities). Then, for counterclockwise (CCW) orientation, $\oint_{|z|=r_2} f(z)dz = \oint_{|z|=r_1} f(z)dz$

Why this holds? For multiply connected regions with analytic functions, the generalized Cauchy theorem states $\oint_{C} f(z)dz + \sum_{k}\oint_{C_k}^{\text{(CW)}} f(z)dz= 0$.

For our annulus with one outer boundary (∣z∣ = r₂) and one inner boundary (∣z∣ = r₁): $\oint_{|z|=r_2} f + \oint_{|z|=r_1}^{\text{(CW)}} f(z)dz = 0 \rightarrow[\text{Since clockwise (CW) integration is the negative of CCW integration:}] \oint_{|z|=r_2} f(z)dz = \oint_{|z|=r_1} f(z)dz.$

• Multiply connected region: sum over boundaries (all CCW). Let R be the region inside C and outside the inner circles $C_1, \dots, C_n$. If f is analytic on an open set containing $\overline{R}$ (the closure of R), then, $\oint_C f(z)dz = \sum_{k=1}^n \oint_{C_k} f(z)dz$.

Example 1: f(z)= $z^3$ (entire), take C: |z| = 2, and $C_1$: |z| =1. The region R = {z ∈ ℂ: 1 < ∣z∣ < 2} is an annulus. Then, $\oint_{|z|=2} z^3 dz =\oint_{|z|=1} z^3dz=0$. The identity holds trivially, and also illustrates deformation (you can slide the outer loop to the inner one through the analytic annulus).

Example 2: $f(z) = \frac{1}{z}$. The region R = {z ∈ ℂ: 1 < ∣z∣ < 2} is an annulus. The closure, $\overline{R}$ = {z : 1 ≤ ∣z∣ ≤ 2} is contained in the open set U = {z: 0.5 < ∣z∣ < 2.5} where f is analytic (since $0 \notin U$). By the theorem, $\oint_{|z|=2} \frac{1}{z} dz =\oint_{|z|=1} \frac{1}{z}dz = 2\pi i$.

Example 3. Let $f(z)=\dfrac{1}{z-a}$, with a lying strictly inside $C_1$ but outside all other holes and not on C. Then, $\oint_C f(z)dz = \sum_{k=1}^n \oint_{C_k} f(z)dz = \oint_{C_1} \frac{dz}{z-a} = 2\pi i.$