The Antiderivative Theorem

Do, or do not. There is no try, Yoda.

Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$.

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

Properties

• Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

• The Residue Theorem states that the integral of a function f(z) around a simple (doesn't cross itself), and positively oriented (counter-clockwise) contour γ is equal to 2πi times the sum of the residues of all singularities inside the contour, $\int_{\gamma} f(z)dz = 2\pi i \sum Res(f, z_k)$ where $z_k$ is a reside inside γ. f must be analytic inside the contour γ, except for a finite number of isolated singularities.

1. For a simple pole at a point $z_k$ (i.e., the denominator has a simple root) is calculated using the formula $Res(f, z_k) = \lim_{z \to z_k}(z-z_k)f(z)$.
2. For a pole of order m, $Res(f, z_k) = \frac{1}{(m-1)!}\lim_{z \to z_k} \frac{d^{m-1}}{dz^{m-1}}[(z-z_k)^mf(z)]$

• Proposition. Linearity of the contour integral, $\int_{\gamma} (af(z) + bg(z))dz = a\int_{\gamma} f(z)dz + b\int_{\gamma} g(z)dz$
• Proposition. Properties of contour integrals under path manipulation. Let γ be a contour, defined by a function $\gamma: [a, b] \to \mathbb{C}$ and let f be a continuous functions $f: \gamma^* \to \mathbb{C}$ defined along the image of ᵞ. Then,

1. Reversal of orientation. $\int_{-\gamma} f(z)dz = -\int_{\gamma} f(z)dz$ where $-\gamma:[a,b] \to \mathbb{C}$ is the reverse of the contour (traversing the same path in the opposite direction) defined by $(- \gamma)(t)=\gamma(a+b-t)$. This property states that reversing the direction of a contour changes or flips the sign of the integral. Intuitively, this is analogous to how reversing the limits of integration in real analysis changes the sign: $\int_a^b f(x)dx = -\int_b^a f(x)dx$. In complex analysis, the orientation of the contour matters because the integral depends on the direction in which we traverse the path.
2. Additivity under subdivision. Suppose a < c < b, let split $\gamma$ into two sub-contours $\gamma_1 = \gamma|_{[a, \gamma_1]} \text{ and } \gamma_2 = \gamma|_{[c, b]}$, then $\int_{\gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. This property states that integrating over the whole contour is the same as integrating over the pieces successively. This is the complex analogue of the additive property of definite integrals: $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx $ for a < c < b.
3. Invariance of Contour Integrals Under Reparameterization. Let $\tilde{\gamma}$ be a contour, defined by a function $\tilde{\gamma}: [c, d] \to \mathbb{C}$. If $\tilde{\gamma}$ is another parameterization of the same oriented path $\gamma$ meaning there exists a one-to-one, continuously differentiable map $\psi: [c,d]\to[a,b]$ with a positive derivative $\psi'(t)>0$ such that $\tilde{\gamma}(t) = \gamma(\psi(t))$, then $\int_{\gamma} f(z)dz = \int_{\tilde{\gamma}} f(z)dz$

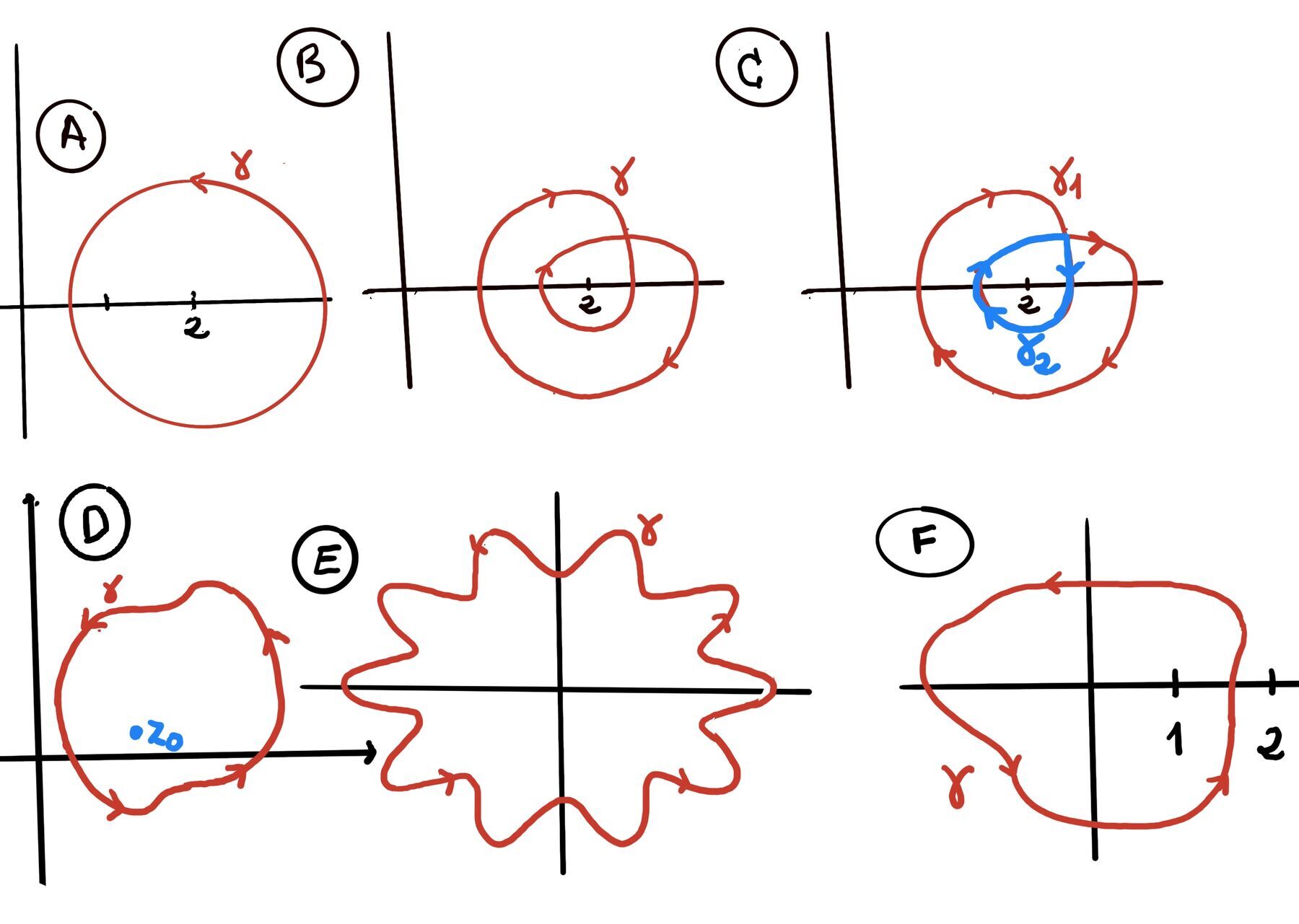
• Deformation of Contours. If two contours $\gamma_1$ and $\gamma_2 $ are homotopic (i.e., one can be continuously deformed into the other without crossing any singularities of f) in a domain where f(z) is analytic, then: $\int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z)dz.$

• Fundamental Theorem of Calculus for Contours. Suppose $\gamma$ is a contour (piecewise smooth path) from a to b, f is defined on a domain D containing $\gamma^*$ (the image of $\gamma$) and admits a primitive (antiderivative) F on D (i.e., $F'(z) = f(z)$), then $\int_{\gamma} f(z)dz = F(\gamma(b)) - F(\gamma(a))$. In particular, if $\gamma$ is a closed contour (i.e., $\gamma(a)=\gamma(b)$), this integral evaluates to zero, $\int_{\gamma} f(z)dz = 0.$

• Estimation Theorem or the Triangle Inequality for Integrals. The triangle inequality for integrals in complex analysis states thatfor any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(t) = u(t) + iv(t), t a real parameter), the following holds: $∣\int_a^b f(t)dt| \leq \int_a^b |f(t)|dt$.

• Estimation Lemma (ML Inequality) for contour integrals. For any continuous complex function $f:[a,b] \to \mathbb{C}$ on a closed real interval [a,b] (f(z) = u(x, y) + iv(x, y)) with f bounded by some constant M along the entire contour, |f(z)| ≤ M for all $z \in \gamma^*$ (the image/trace of the contour in the complex plane), the following holds: $∣\int_\gamma f(z)dz| \leq M \cdot l(\gamma)$ where l(γ) is the arc length of the contour γ given by $\int_a^b |\gamma^{'}(t)|dt = \int_a^b \sqrt{x'(t)^2 + y'(t)^2} \text{ where } \gamma(t) = x(t) + iy(t)$.

• Jordan’s curve theorem. Any simple closed curve (a continuous loop in the plane that does not intersect itself) separates the plane into two disjoint connected regions: one interior (bounded) and one exterior (unbounded). The curve itself is the boundary of both regions. In other words, it partitions the plane into exactly three disjoint sets:

1. The Curve itself ($\gamma$).
2. The Interior (Int($\gamma$)) is the finite area enclosed by the curve (e.g., if you draw a circle on a piece of paper, the interior region would be everything inside the circle). It is a bounded, simply connected region.
3. The Exterior (Ext($\gamma$)) is the infinite area outside the curve (e.g., using the same circle example, the exterior region would include all points on the paper that are not inside the circle). It is an unbounded region.

• Definition. Let $\gamma: [α, β] → \mathbb{C}$ be a piecewise smooth, closed curve (so γ(α) = γ(β)), the winding number of γ about $z_0$, a complex point not on the curve $z_0$ ∉ γ([α, β]), also known as the index of $z_0$ with respect to γ, is defined as $n(\gamma, z_0) = Ind_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}dt$ (the total number of counterclockwise turns that the object makes around $z_0$).

Cauchy’s Theorem in Complex Analysis

• Cauchy’s theorem (Classical “Green’s theorem” version). Let $\Omega \subset \mathbb{C}$ be an open domain. Suppose f = u + iv is analytic in $\Omega$ and its partial derivatives ( $u_x,u_y,v_x,v_y$) are continuous in $\Omega$. If $\gamma$ is a positively oriented, piecewise-smooth $C^1$, simple closed contour with $\gamma^* \cup \operatorname{Int}(\gamma) \subset \Omega$ (its path and interior both lie inside Ω), then $\oint_{\gamma} f(z)dz = 0.$

• Cauchy’s Theorem (Cauchy–Goursat). This is the more powerful version, as it removes the need for continuous partial derivatives. If f is analytic in an open set containing a simple closed contour γ and its interior $\gamma^*\cup\operatorname{Int}(\gamma)$, then $\oint_{\gamma} f(z)dz = 0$.

• Cauchy’s Theorem for simply connected domains. If a function f is analytic (a function that is complex-differentiable at every point within a domain, i.e., well-behaved and smooth, with no sharp corners, breaks, or singularities like division by zero) throughout a simply simple connected domain D then $\oint_C f(z)dz = 0$ for every closed contour C lying in D.

• General Cauchy Theorem for Multiply Connected Domains. Let $R$ be the multiply connected region (with n holes) inside $C$ but outside of every $C_k$ (each $C_k$ surrounds only one hole in the domain), $R = Int(C) \setminus \bigcup_{k=1}^n \overline{​Int(C_k​)}$​, and let $f(z)$ be analytic on $R$. Now, let $\Gamma$ be any general closed contour (not necessarily simple) that lies entirely in R. This $\Gamma$ can wind around the “holes” (the regions inside each $C_k$) in any way it likes (this is the winding number or index of $\Gamma$ around each hole), the integral over $\Gamma$ is: $\oint_{\Gamma} f(z)dz = \sum_{k=1}^n m_k \oint_{C_k} f(z)dz$.

The Anti-Derivative Theorem

The Anti-Derivative Theorem. Let f be a continuous function on a region G (a region is an open, connected set). Then, the following statements are equivalent:

1. f has an antiderivative F throughout G. This means a function F exists such that F is analytic and F’(z) = f(z) for any z ∈ G.
2. The integral of f over every closed contour $\gamma$ in $G$ is zero: $\oint_\gamma f(z)dz = 0$.
3. The integral of $f$ is path independence. For any two points $a$ and $b$ in $G$, the value of $\oint_\gamma f(z)dz$ is the same (constant) for any contour $\gamma$ in $G$ that starts at a and ends at b.

Proof.

(1) ⇒ (2)

Let $\gamma$ be any closed contour in G. Let’s parameterize it by z(t) for t in an interval $[\alpha, \beta]$. Since the loop is closed, it starts and ends at the same point, let’s call it a, $z(\alpha) = z(\beta) = a$.

Now, let’s write out the integral using its definition:

$$ \begin{aligned} \oint_\gamma f(z)dz &=\int_\alpha^\beta f(z(t)) \cdot z'(t) dt \\[2pt] &=[\text{Since we assumed F'(z) = f(z)}] \int_\alpha^\beta F'(z(t)) \cdot z'(t) dt \\[2pt] & [\text{By the chain rule, }] \frac{d}{dt} \left( F(z(t)) \right) = F'(z(t)) \cdot z'(t) \\[2pt] &=\int_\alpha^\beta \frac{d}{dt} \left( F(z(t)) \right) dt \\[2pt] &= [\text{By the Fundamental Theorem of Calculus, }] \left[ F(z(t)) \right]_\alpha^\beta = F(z(\beta)) - F(z(\alpha)) \\[2pt] &= [z(\alpha) = z(\beta) = a] F(a) - F(a) = 0. \end{aligned} $$

The proof for $(1) \implies (3)$ is almost identical. The integral from $a$ to $b$ would be $F(z(\beta)) - F(z(\alpha)) = F(b) - F(a)$, which depends only on the endpoints, not the path.

(2) ⇒ (3). Let $\gamma_1 \text{ and } \gamma_2$ be two contours or paths from a to b in G.

Consider the new contour $\Gamma = \gamma_1 - \gamma_2$ where $-\gamma_2$ is the path $\gamma_2$ but traversed in reversed (from b back to a). This path starts at a, goes to b (via $\gamma_1$), and then returns to a (via $-\gamma_2$). Therefore, it is a closed contour.

By our assumption 2, $\oint_{\gamma_1 - \gamma_2} f(z)dz = 0$. Using the linearity of integrals, we can split the integral over $\Gamma, \int_{\gamma_1} f(z)dz + \int_{-\gamma_2} f(z)dz = 0.$

A key property of contour integrals is that reversing the path negates the value, $\oint_{\gamma_1}f(z)dz - \oint_{\gamma_2}f(z)dz = 0 \leadsto \oint_{\gamma_1}f(z)dz = \oint_{\gamma_2}f(z)dz$.

This shows that the integral’s value only depends on the endpoints (a and b), not the path taken. This is the definition of path independence.

3 ⇒ 1

Suppose the integral $\oint_{\gamma}f(z)dz$ depends only on the initial and final points of a contour γ lying in G. Since $G$ is a region (connected), we can fix a starting point $z_0$ anywhere in G. Let’s define a function F(z) for any other point z in G as follows: $F(z) = \oint_{\gamma}f(z)dz$ where γ is any contour lying in G from $z_0$ to z.

F is well-defined (meaning it gives a single, unambiguous value) because we are assuming path independence (3). It doesn’t matter which path we take from $z_0$ to z, the integral’s value will be the same, $F(z) = \oint_{\gamma}f(z)dz = \int_{z_0}^z f(z)dz$.

We aim to prove that F’(z) = f(z). Let z ∈ G and consider $|\frac{F(z+h) - F(z)}{h} - f(z)| = |\frac{\int_{z_0}^{z+h} f(ξ)dξ - \int_{z_0}^z f(ξ)dξ}{h} - f(z)|$

Because of path independence (F is well defined), we can choose our integration paths to be convenient. Let’s consider a path from $z_0$ to z + h to be a path from $z_0$ to z, followed by a straight line segment from z to z + h (This is allowed because G is an open set, so for a small enough h, the straight line segment from z to z + h will be entirely contained within G). Now we can split the first integral: $\int_{z_0}^{z+h} f(ξ)dξ - \int_{z_0}^z f(ξ)dξ = (\int_{z_0}^{z} f(ξ)dξ + \int_{z}^{z+h} f(ξ)dξ) - \int_{z_0}^z f(ξ)dξ = \int_{z}^{z+h} f(ξ)dξ$ (the $\int_{z_0}^{z} f(ξ)dξ$ terms cancel) where the integral is over the straight line from z to z + h.

Hence, $|\frac{\int_{z_0}^{z+h} f(ξ)dξ - \int_{z_0}^z f(ξ)dξ}{h} - f(z)| = |\frac{\int_{z}^{z+h} f(ξ)dξ}{h} - f(z)|$.

Since G is open and z ∈ G, there is a $\delta_0 \gt 0$ such that $B(z; \delta_0) \subseteq G$. When $|h| \lt \frac{\delta_0}{2}$, the straight line joining z and z + h is contained in G. Therefore, we choose the straight line (contour) from z to z + h for the above integral when $|h| \lt \frac{\delta_0}{2}$.

Then, $\frac{\int_{z}^{z+h} f(ξ)dξ}{h} - f(z) = \frac{\int_{[z, z+h]} (f(ξ) - f(z))dξ}{h}$ where $\int_{[z, z+h]}$ indicates the straight line (contour) from z to z + h, and we can write the constant f(z) as an integral over the straight line $[z, z+h]$. The path has length $L = |(z+h) - z| = |h|$; we can parameterize the path as $\gamma(t) = z + th$ for $t \in [0, 1], \gamma'(t) = h$.

Then, $\int_{[z, z+h]} f(z)dξ = \int_0^1 f(z) \cdot \gamma'(t) dt = \int_0^1 f(z) \cdot h dt = f(z) \cdot h \cdot t\bigg|_{0}^{1} = f(z)\cdot h$.

Therefore, we can write $f(z) = \frac{1}{h} \int_z^{z+h} f(z)d\xi$.

By the Estimation Theorem, $|\frac{\int_{[z, z+h]} (f(ξ) - f(z))dξ}{h}| \le \frac{1}{|h|} \int_{[z, z+h]} |f(ξ) - f(z)| dξ$

Analicity implies continuity and by continuity of f, given $\epsilon \gt 0$, there is a $\delta \gt 0$ such that whenever $|ξ -z| \lt \delta, |f(ξ) - f(z)| \lt \epsilon$ (as $\xi$ gets closer to $z, f(\xi)$ gets closer to $f(z)$).

So given $\epsilon \gt 0$, choose $\delta_1 = min(\delta, \delta_0)$ so that whenever $|ξ -z| \lt \delta_1, |f(ξ) - f(z)| \lt \epsilon \text{ and } \frac{1}{|h|} \int_{[z, z+h]} |f(ξ) - f(z)| dξ \lt \epsilon \frac{1}{|h|} \cdot \int_{[z, z+h]} dξ = \epsilon$.

Therefore, given $\epsilon \gt 0$, we have found a $\delta_1$ so that whenever $|ξ -z| \lt \delta_1, |\frac{F(z+h) - F(z)}{h} - f(z)| \lt \epsilon$. So F is differentiable at every point z ∈ G and F’(z) = f(z).