Introduction

A complex function $f(z)$ maps $z = x + iy \in \mathbb{C}$ to another complex number. For example: $f(z) = z^2 = (x + iy)^2 = x^2 - y^2 + 2ixy, f(z) = \frac{1}{z}, f(z) = \sqrt{z^2 + 7}$.

A contour is a continuous, piecewise-smooth curve defined parametrically as: $z(t) = x(t) + iy(t), \quad a \leq t \leq b$. Examples of contours:

A straight line between two points $z_0$ and $z_1$ is parametrized as: $\gamma(t) = z_0 + t(z_1 - z_0), t \in [0, 1]$.
Unit Circle: $\gamma(t) = e^{it} = \cos t + i \sin t, t \in [0, 2\pi]$. This traces a circle of radius 1 centered at the origin.
Ellipse: $\gamma(t) = a \cos t + i b \sin t, a, b > 0$. If we write z = x + i·y, then: x(t) = acos(t), y(t) = bsin(t). Solve for cosine and sine $\cos t=\frac{x}{a}, \sin t=\frac{y}{b}$ which is valid because a, b > 0 so we can divide by them. The fundamental identity $\cos^2(t)+\sin^2(t)=1$ holds for all t. Substitute the expressions above: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. That’s the standard Cartesian equation of an ellipse centered at the origin, centered at the origin with semi-axes a (along x) and b (along y).
Parabola: $\gamma(t) = t + it^2, t \in [-2, 2]$. This traces a parabola in the complex plane (real part linear, imaginary part quadratic).

Definition (Smooth Contour Integral). Let ᵞ be a smooth contour (a continuously differentiable path in the complex plane), $\gamma: [a, b] \to \mathbb{C}$. Let $f: \gamma^* \to \mathbb{C}$ be a continuous complex-valued function defined on the trace $\gamma^*$ of the contour (i.e. along the image of $\gamma$). Then, the contour integral of f along $\gamma$ is defined as $\int_{\gamma} f(z)dz := \int_{a}^{b} f(\gamma(t)) \gamma^{'}(t)dt$.

In this definition, we integrate the function f along the path traced out by $\gamma(t)$. The term $\gamma^{'}(t)$ (the derivative of $\gamma$) accounts for the direction and speed of traversal along the path. This definition essentially transforms or converts the complex line integral into a regular real integral over the interval [a, b] via the parametrization $\gamma(t)$. The factor $\gamma'(t)dt = d\gamma$ represents an infinitesimal step along the curve, so $f(\gamma(t))\gamma'(t)dt$ is the infinitesimal contribution to the integral from that step.

Cauchy Integral Formula

Theorem. Cauchy Integral Formula. If a function f is analytic in a simply connected domain D and γ is a simply closed contour (positive orientated) in D. Then, for any point $z_0$ inside γ we have $f(z_0) = \frac{1}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{z-z_0}dz$ (Figure D).

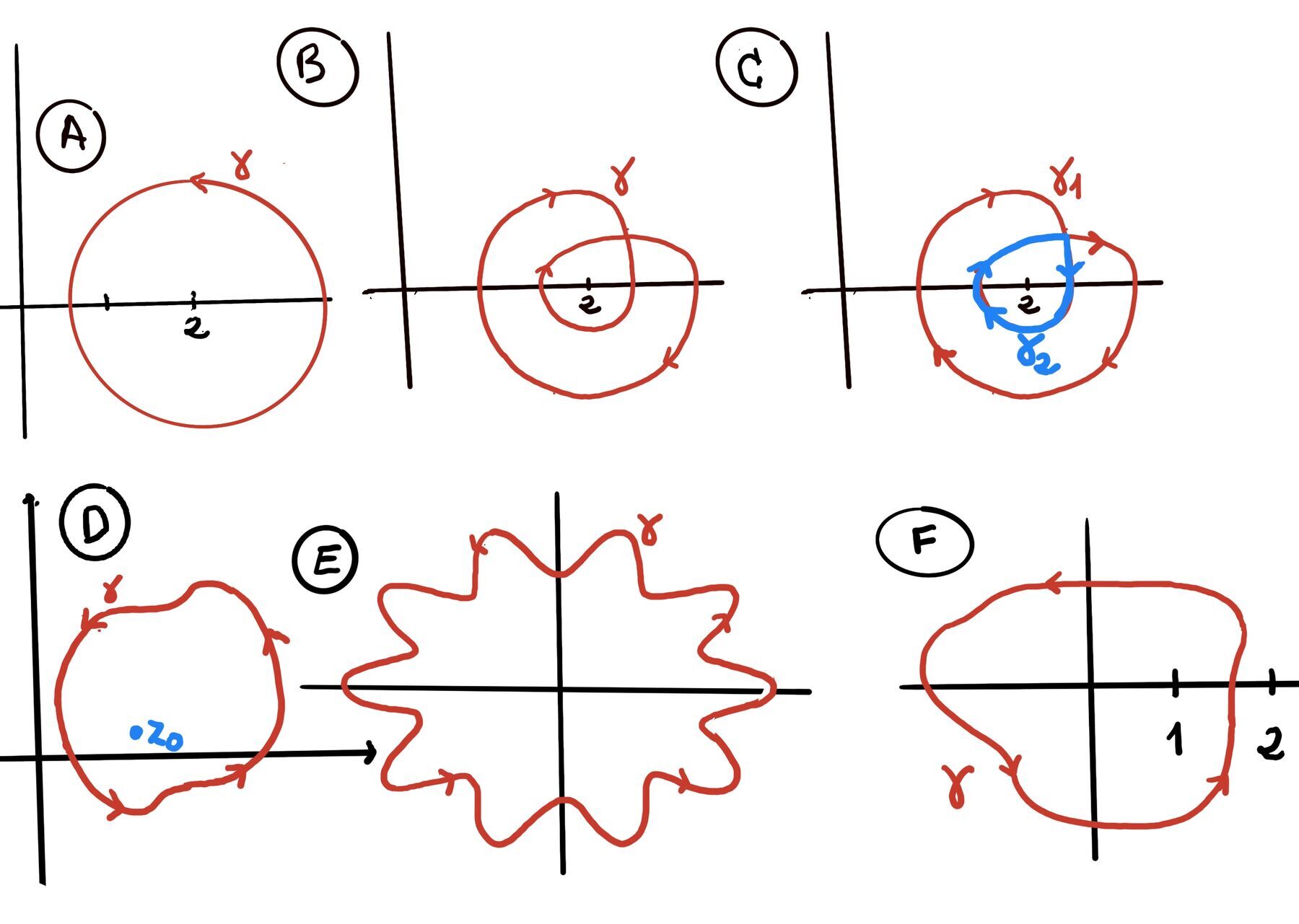
Cauchy Integral Formula

It states that the value of an analytic function at any point z₀ is completely determined by the values the function takes on any simple closed curve that encircles the point. If you know the function’s values on the boundary, you know everything about the function’s behavior inside that boundary. This is quite unlike anything you’ve probably encountered with functions of real variables.

A more generalized version is as follows: $f^{(n)}(z_0) = \frac{n!}{2\pi i}\cdot \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz$.
Cauchy Integral Formula (Winding Number Lemma). Let γ be a closed rectifiable curve in ℂ, f analytic on an open set containing γ and its interior. For any point a not on γ, the Cauchy Integral Formula states: $\oint_{\gamma} \frac{f(z)}{z-a}dz = 2\pi i \cdot n(\gamma, a) \cdot f(a)$
The winding number is defined as $n(γ, a) = \frac{1}{2πi}\oint_\gamma \frac{dz}{z-a}$. This represents the net number of times γ winds around a counterclockwise.
For simple closed curves with positive orientation n(γ, a) = 1 if a is inside γ, 0 if outside.
For multiple windings n(γ, a) counts the net winding (e.g., 2 for two counterclockwise loops, -1 for one clockwise loop).
The formula reduces to the basic Cauchy Integral Formula when n(γ, a) = 1.
The formula can be used to calculate integrals: $\int_{\gamma} \frac{f(z)}{z-z_0}dz = 2\pi i \cdot f(z_0), \int_{\gamma} \frac{f(z)}{(z-z_0)^{(n+1)}}dz = \frac{2\pi i}{n!} \cdot f^{(n)}(z_0)$
Key Conditions:
Analyticity: $ f(z) $ must be analytic (holomorphic) inside and on $\gamma$.
Contour $ C $: $\gamma$ is a simple closed curve (e.g., a circle, ellipse). A simple closed curve is a curve that has no self-intersections and is closed, meaning it starts and ends at the same point.
Point $z_0$: $z_0$ must lie inside $\gamma$. If $z_0$ is outside $\gamma$, the integral is zero.

Analyticity Implies Infinite Differentiability

Theorem. Analyticity Implies Infinite Differentiability. Suppose that f is analytic (or holomorphic) in an open set G. Then, (i) f' is also analytic in G; (ii) f has derivatives of all orders ($f', f'', f''', \dots$) in G.

Proof.

The key to the proof is demonstrating that the second derivative, $f''(a)$, exists for an arbitrary point $a \in G$. The derivative of $f'(z)$ is $f''(z)$; if $f''(z)$ exists, $f'(z)$ is analytic.

Fix $a \in G$. Since G is open, choose r > 0 so that the closed disk $\overline{B(a;2r)}\subset G$. Let $ \gamma=\partial B(a;2r)$ (positively oriented circle). Because f is analytic in G, Cauchy’s formula for the first derivative holds on $\operatorname{Int}\gamma$: $f'(z) = \frac{1}{2\pi i}\oint_{\gamma} \frac{f(w)}{(w-z)^2}dw$.

We are going to apply the same reasoning as the previous proof:

$$ \begin{aligned} \frac{f'(a+h)-f'(a)}{h} &\text{ [We apply the Cauchy’s Integral Formula for the First Derivative to the points a + h and a] } \\[2pt] &=\frac{1}{2\pi i h} \left[ \oint_{\gamma} \frac{f(w)}{(w-a-h)^2}dw - \oint_{\gamma} \frac{f(w)}{(w-a)^2}dw \right] \\[2pt] &\text{Linearity Property of Contour Integrals} \\[2pt] &=\frac{1}{2\pi i h} \oint_{\gamma}\left[ \frac{f(w)}{(w-a-h)^2} - \frac{f(w)}{(w-a)^2} \right]dw \\[2pt] &\text{Combine the fractions inside the brackets using the common denominator} \\[2pt] &=\frac{1}{2\pi i h} \oint_{\gamma} \frac{f(w)}{(w-a-h)^2 (w-a)^2} [(w-a)^2 - (w-a-h)^2]dw \\[2pt] &\text{It simplifies to } A^2 - B^2 = (A-B)(A+B) = h[2(w-a)-h] \\[2pt] &=\frac{1}{2\pi i h} \oint_{\gamma} \frac{f(w)}{(w-a-h)^2 (w-a)^2} [(-h)^2 +2wh - 2ah]dw \\[2pt] &\text{The factor h cancels:} \\[2pt] &=\frac{1}{2\pi i} \oint_{\gamma} \frac{f(w)}{(w-a-h)^2 (w-a)^2} [-h +2w - 2a]dw \\[2pt] &=\frac{1}{2\pi i} \oint_{\gamma} \frac{f(w)}{(w-a-h)^2 (w-a)^2} [2w - 2a -2h + h]dw \\[2pt] &=\frac{1}{2\pi i} \oint_{\gamma}\left[ \frac{f(w) \cdot 2(w - a -h)}{(w-a-h)^2 (w-a)^2} + \frac{f(w)h}{(w-a-h)^2 (w-a)^2}\right]dw \\[2pt] &=\frac{1}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2}{(w-a-h) \cdot (w-a)^2} + \frac{h}{(w-a-h)^2 (w-a)^2}\right]dw \text{ (i) } \end{aligned} $$

We conjecture that $f''(a) = \frac{2}{2\pi i} \oint_{\gamma} \frac{f(w)}{(w-a)^3}dw$. We examine the error between the difference quotient (i) and the conjectured integral:

$$ \begin{aligned} |Error| &=|\frac{f'(a+h)-f'(a)}{h} -\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw| \\[2pt] &=\text{(i)} \\[2pt] &=|\frac{1}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2}{(w-a-h) \cdot (w-a)^2} + \frac{h}{(w-a-h)^2 (w-a)^2} -\frac{2}{(w-a)^3} \right]dw| \\[2pt] &\text{Combine the fractions inside the brackets using the common denominator} \\[2pt] &=|\frac{1}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2(w-a) -2(w-a-h)}{(w-a-h) \cdot (w-a)^3} + \frac{h}{(w-a-h)^2 (w-a)^2} \right]dw| \\[2pt] &=|\frac{1}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2h}{(w-a-h) \cdot (w-a)^3} + \frac{h}{(w-a-h)^2 (w-a)^2} \right]dw| \\[2pt] &\text{Combine the fractions inside the brackets using the common denominator and move h outside the integral} \\[2pt] &=|\frac{h}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2(w-a-h)+(w-a)}{(w-a-h)^2 \cdot (w-a)^3}\right]dw| \end{aligned} $$

Bounding the Error with M L-Estimation:

Contour Length L. The length of the contour $\gamma$ is $L = 2\pi (2r) = 4\pi r$.
Bound for |f(w)|: Since f is analytic, it is continuous on the compact (closed and bounded) contour $\gamma$. By the Extreme Value Theorem (Weierstrass Theorem), f is bounded: $|f(w)| \le M$ for some M, $M = \max_{w \in \gamma} |f(w)|$.
Denominator Bounds. Bound for |w - a|: For w on the circle $\gamma, w \in \gamma^*$, the distance is exactly |w - a| = 2r. Bound for |w -a -h|: We chose |h| < r. By the Reverse Triangle Inequality: $|w-a-h| \ge ||w-a| - |h|| = |2r - |h||$. Since |h| < r, then $-|h| > -r \leadsto 2r - |h| > 2r - r = r > 0, |w-a-h| \gt r$.
Numerator Bound: $|2(w-a-h) + (w-a)| = |3(w-a) - 2h| \le |3(w-a)| + |-2h| = 3|w-a| + 2|h| < 3(2r) + 2(r) = \mathbf{8r}$

$$ \begin{aligned} |\frac{f'(a+h)-f'(a)}{h} -\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw| &=|\frac{h}{2\pi i} \oint_{\gamma} f(w)\left[ \frac{2(w-a-h)+(w-a)}{(w-a-h)^2 \cdot (w-a)^3}\right]dw| \\[2pt] &\text{By the ML-Estimation Lemma} \\[2pt] &\le \frac{|h|}{2\pi} M \frac{8r}{r^2\cdot (2r)^3} 4\pi r\\[2pt] &\text{Simplify the factors:} \\[2pt] &=\frac{|h| 32r^2}{16r^5} = \frac{|h|2M}{r^3} \end{aligned} $$

$0 \le |\frac{f'(a+h)-f'(a)}{h} -\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw| \le \frac{2M}{r^3}|h|$

Since $M$ and $r$ are fixed constants, as $h \to 0$, the upper bound $\frac{2M}{r^3}|h|$ approaches $0$. $\lim_{h \to 0} \frac{2M}{r^3}|h| = \lim_{h \to 0} 0 = 0 \leadsto[\text{By the Squeeze Theorem}]$

$\lim_{h \to 0} |\frac{f'(a+h)-f'(a)}{h} -\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw| = 0 \leadsto \lim_{h \to 0} \frac{f'(a+h)-f'(a)}{h} -\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw = 0$.

Since $\frac{2}{2\pi i} \oint_\gamma \frac{f(w)}{(w-a)^3}dw$ is constant related to h, the second derivative exists, and its value is $f''(a) = \frac{2}{2\pi i}\oint_\gamma \frac{f(w)}{(w-a)^3}dw$

Since $f''(a)$ exists for an arbitrary point $a \in G$, $f'(z)$ is differentiable on $G$, meaning $f'$ is analytic in $G$. (This proves part (i)).

We normally use the following notation: $f''(z) = \frac{2!}{2\pi i}\oint_\gamma \frac{f(w)}{(w-z)^3}dw, \forall z \in \mathcal{Int}(\gamma)$

(ii) We proved that if f is analytic in G then f’ is analytic in G by (i). Since f’ is analytic in G, we can replace f by f’ in the previous statement, so f’’ is analytic in G, and we can continue this process indefinitely, so f is infinitely differentiable in G. Furthermore, this derivation provides the General Cauchy Integral Formula for Derivatives for any order n.